散布図は、一度は目に触れたことのある方は多いと思います。
しかし、なぜ散布図がQC 7つ道具の一つに挙げられているのか、考えたことはあるでしょうか?
- 「QC 7つ道具として、どう活用するのか?」
- 「散布図から何が読み取れるのか?」
- 「見やすい散布図の作り方を知りたい!」
このような疑問や希望をお持ちの方に向けた記事です。10分で理解できるよう、わかりやすく簡潔に解説します。
品質管理にどう役立つのか、という着眼点で解説しましたので、ぜひ最後まで読んで参考にしていただければと思います。
散布図って何?

見たことあるよ。点がたくさんあるグラフだよね?
散布図は、縦軸と横軸に量や大きさのデータを点で表示したグラフです。
基本的に、縦軸と横軸の変数は何でもよいのですが、QC 7つ道具の観点では、「特性」と「要因」という分類で規定します。
「特性」とは「結果」のこと。「要因」とは「要因、または原因」を表します。
以下の3つのケースに分類されます。
①:縦軸「特性」、横軸「要因」
②:縦軸「特性」、横軸「特性」
③:縦軸「要因」、横軸「要因」
「特性」と「要因」の関係性を視覚化する手法では、「特性要因図」も良く用いられます。別の記事で、合わせてご覧ください。
なぜ散布図を使うの?

「特性」とか「要因」とか、むずかしそうな言葉を使うのは何のため?
目的・用途・メリット
- 相関関係を明確にする
グラフで視覚的に把握でき、変数どうしの関連性(相関関係)が分かりやすくなります。 - 因果関係を明確にする
「特性」と「要因」の間に相関関係があるということは、すなわち因果関係のあることを意味します。
原因調査を目的とした活用例も多いです。 - データ選定の指標
データ選定を効率的に行うことができます。
例えば、集計データの中から、一つのサンプルを選ぶ場合、ただ単に最大値や最小値を選ぶと、異常点(外れ値)を引く心配もあります。
全体の分布を見た上で、選定の意図にあった最良点を選ぶことで、選定ミスを防げます。
どのように作るの?
手順
5つのステップで、作っていきます。
- データ収集
- 縦軸と横軸の設定
- 座標軸のスケールの設定
- グラフ化する
- 必要事項を記入
- データ収集
元となるデータを集めます。
データ数量があまりに少ないと相関性を判別できない場合もあるため、できればデータ数(標本数)は30~50程度を用意しましょう。 - 縦軸と横軸の設定
データを横軸(x軸)と縦軸(y軸)に割り振りましょう。
「要因」と「特性」の関係を見る際には、”y=ax+b”のように、xがインプット、yがアウトプットとなるので、「要因」を横軸、「特性」を縦軸に取ります。 - 座標軸のスケールの設定
次に、座標軸のスケールを決めます。
最小値と最大値を包括できる範囲で目盛りを設定します。 - グラフ化する
横軸と縦軸の交差する位置に点を打ちます。
同じ箇所に複数の点が重なる場合は、点の位置を少しずらすか、丸で囲うなどして、工夫しましょう。 - 必要事項の記入
具体的には、作成目的、集計期間、製品名や工程名、作成者、作成日などの情報を記載します。

きちんと他の人に伝えることが大事なんだね。
見やすさを心がける
- 基準線を入れる
- 近似曲線を入れる
- 系列を分けて表示する
- 基準線を入れる
グラフ中に基準線を加えることで、相対的な位置関係が見やすくなります。
品質管理の実用例としては、規格の上下限値などを記載したりします。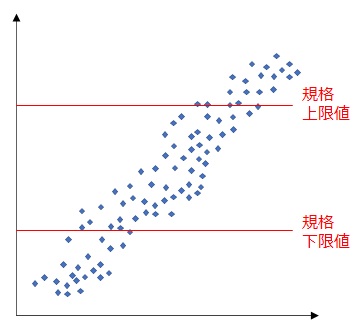
- 近似曲線を入れる
相関関係が見られる場合には、近似曲線と近似式を加えることで、相関性の強さがさらに見やすくなります。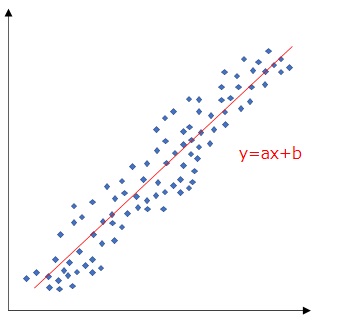
- 系列を分けて表示する
一見、相関性が無いように見えても、なんらかの基準で母集団を複数の要素に分類する(これを層別といいます)と、関係性を見いだせる場合があります。
系列を色分け表示すると、より分かりやすくなります。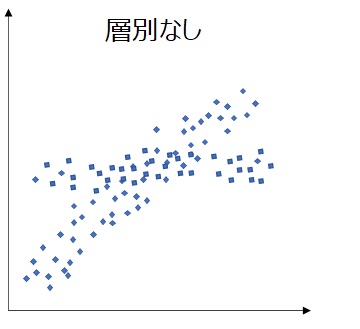
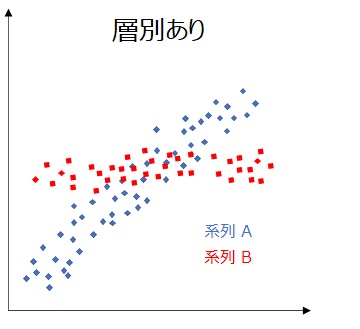

同じデータでも工夫の仕方で見え方が変わってくるね。
散布図から何がわかるの?
相関関係
相関の傾向は、以下の4つに分類されます。
- 正の相関
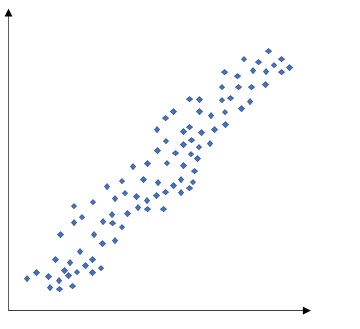
xが増えると、yも増加。
xを「要因」、yを「特性」とする場合、xを管理すれば、yの値を制御できる。 - 負の相関
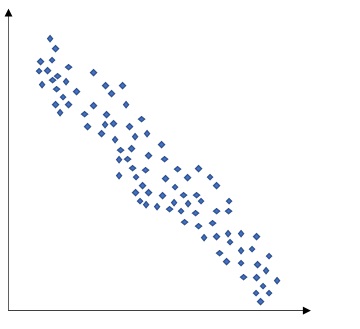
正の相関と反対の関係。 - 相関なし
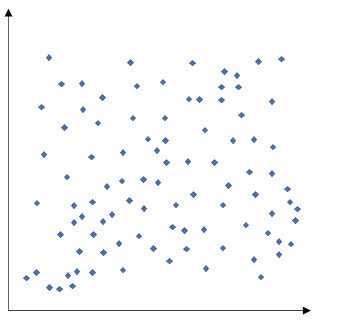
xの増減とyの増減に関連のない状態。
この場合、yの値はxとは別の要因が関係している。 - 直線的でない相関
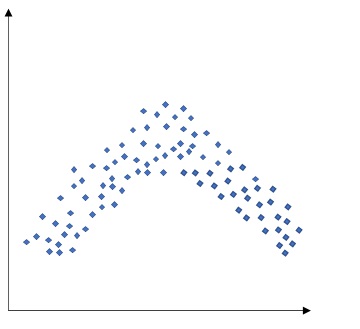
直線的ではないが、増減の関係性がある状態。
変曲点や極大値(極小値)をもつ場合に見られる傾向で、データ選定で最良点を選ぶ場合などには、判断の目安とできる。
散布図を見るポイント
- 異常点はないか
- 疑似相関がないか
- 層別の必要性はないか
- 外挿は適切か
- 異常点はないか
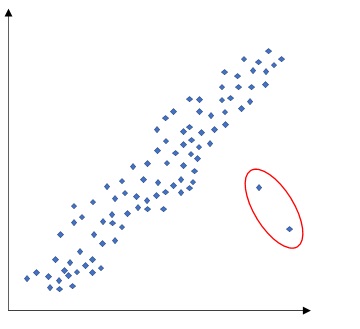
このような異常点が見られる場合は、製造不良や測定ミスの可能性が高いです。
データ選定の際には、単に最大値や最小値を基準とすると、異常点(外れ値)を選んでしまい、選定の意図に沿わない恐れがあります。 - 疑似相関がないか
疑似相関(見かけ上の相関、偽相関)とは、実際には因果関係がないのに、別の見えていない要因によって、関連性があるように見える状態です。
よく例に挙げられるのが、「足の大きさと算数のテストの点数」といった関係です。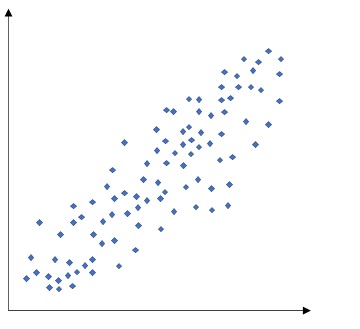
一見、正の相関に見えますが、「足の大きさ」と「テストの点数」に因果関係があるわけではなく、「学年」という要因が抜けているのです。
この散布図を学年で層別してみましょう。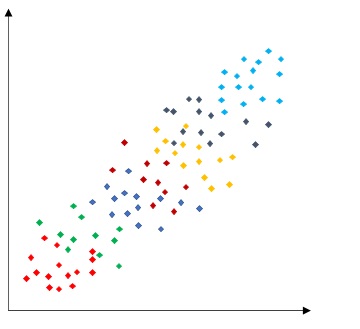
学年ごとに偏りがあり、同じ学年どうしで見てみると全く相関関係はありません。
このように、見えていない要因(潜伏変数)はないか、因果関係がきちんと説明できるか、ということに注意する必要があります。 - 層別の必要性はないか

上記でも説明した通り、複数の要素に分類(層別)すると、相関を見いだせる場合があります。
製造業の事例としては、作業者、装置、材料ロット、作業方法などの4Mの要素に着目して分類すると、関係性が見えてくることがあります。
4Mとは、Man(人)、Machine(機械)、Material(材料)、Method(方法)のことで、例えば、特定の装置や作業者で相関が出るような場合は、なんらかの異常や特徴が潜んでいるのかもしれません。 - 外挿は適切か
外挿とは、範囲外の結果を推定して求めることを表します。
例えば、以下の例では集計データは左下に集中していますが、この状態で近似曲線を引いて範囲外の結果を算出するようなイメージです。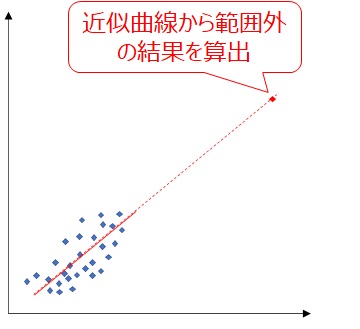
ここで、以下に注意が必要です。
①:集計データの範囲が狭い場合
②:近似曲線の相関精度が低い場合
③:離れすぎた点を外挿で求める場合
外挿する場合、近似曲線の誤差が比例して影響するので、不適切でないか確認しながら実施しましょう。

キチンと使いこなして、傾向を見抜く!
こてつ経験談
外挿のトラップ
とある製品の開発に携わったとき、試作品の温度特性を見ることになりました。
パラメータ(温度)を変えたときの性能の変化を見るもので、今後の開発品の設計方針を左右する重要な位置づけの評価でした。
パラメータの水準は、どれほど細かく取るのか、特にやり方が決まっておらず、評価する側に委ねられた状態で、当時の身近な関係者と相談して評価メニューを決めたのです。
無事に測定を完了し、結果をまとめていた時のこと、別部門のメンバーから対象の温度範囲を広げたいことの要請を受けました。
測定はすでに終わっており、温度と性能に関しても綺麗な相関関係が見られていたので、そのまま温度範囲を外挿して、性能の近似曲線を引いてみました。
後で分かったことなのですが、その相関関係は、実測した温度付近までは線形相関があるものの、一定の温度を超えると線形性が失われ、飽和状態になる性質を持つものでした。
手間を省いた代償
もちろん、その当時はそんなこと一切知らず、直線近似した外挿で性能を導いた結果、当然、大はずれの推定値となってしまいます。
ここから先は、大変な苦労をして事態を収拾させたことは言うまでもないですが、本当にイタい目にあいました。
「そんな凡ミスしませんよ~」と言われかねないですが、外挿には、このようなトラップが潜んでいるのです。
追加評価の手間を惜しまず、横着をせずに素直にやっておけば良かった・・と後悔せぬよう、少しでも参考になればと思います。

まとめ
- 散布図
⇒「特性」や「要因」を縦軸と横軸にとって、大きさのデータを点で表示したグラフ - 目的・用途
⇒相関関係、因果関係の明確化、データ選定の指標 - 散布図を見やすくするポイント
⇒基準線、近似曲線、系列の分類(層別) - 散布図を見るポイント
⇒異常点や疑似相関はないか、層別の必要性、外挿は適切か
散布図はExcelで簡単に作れますが、意外と奥が深く、いままで見えなかった傾向も工夫の仕方ひとつで見えるようになってきます。
うまく使いこなして、鋭い考察力を磨いていきましょう。




コメント