「名前も聞いたことないので、一から教えてほしい」
「数式が難しすぎて、全く頭に入らない」
「散布図の作り方まで順を追って教えてほしい」
このような疑問・悩みをお持ちの方に向けた記事です。10分で理解できるよう、わかりやすく簡潔に解説します。
膨大なデータの次元を落とし、二次元の平面図にすることで関係性を見える化して、解決の糸口を見つけ出す強力なツールです。
できるだけ複雑な数式を使わずに、分かりやすく解説しますので、ぜひ最後まで読んで参考にしていただければと思います。
マトリックスデータ解析法って何?

めちゃくちゃ難しそう・・
マトリックスデータ解析法とは
新QC7つ道具のマトリックス図法では、行と列の交点に要素の関連度合いを示した図を紹介しました。
例えば、行の要素には選択肢の候補、列の要素には評価指標をとり、交点には「行✕列」の条件に対応する結果を数値で記載します。
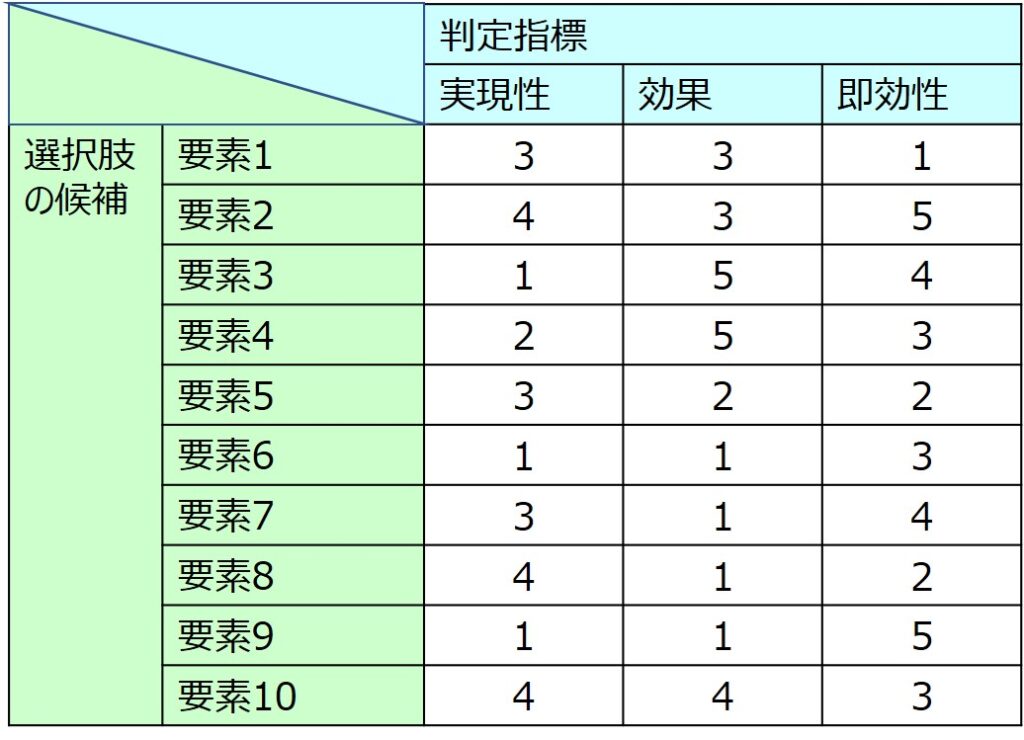
列の要素の数が少ない場合、特に3つ以下のケースでは、列の要素を変数の軸として、3次元のグラフにして視覚化することができます。
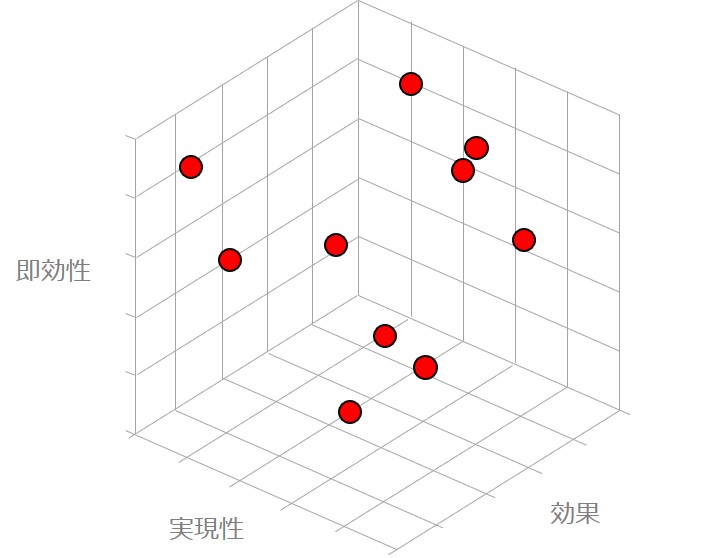
数値の羅列を見ているよりも、わかりやすさ、伝わりやすさが違います。
では、列の要素が4つ以上のケースでは、どのように表現すればよいでしょうか?
列の要素を3つ以下(できれば2つ)に減らして、グラフ化すればよいのです。
ただし、単に要素を2つ選ぶのでは、除外した要素に重要な手がかりが残されているかもしれません。
こんな時に登場するのがマトリックスデータ解析法で、できるだけ元のデータの情報を残しつつ、要素を縮約して二次元の平面図に表し、問題と要因の関係をわかりやすく示す手法のことです。
新QC7つ道具では、言語データを扱うものが多いですが、唯一数値を扱う手法で、統計学では、主成分分析と呼ばれています。
散布図の構成
要素を縮約した散布図の例を示します。
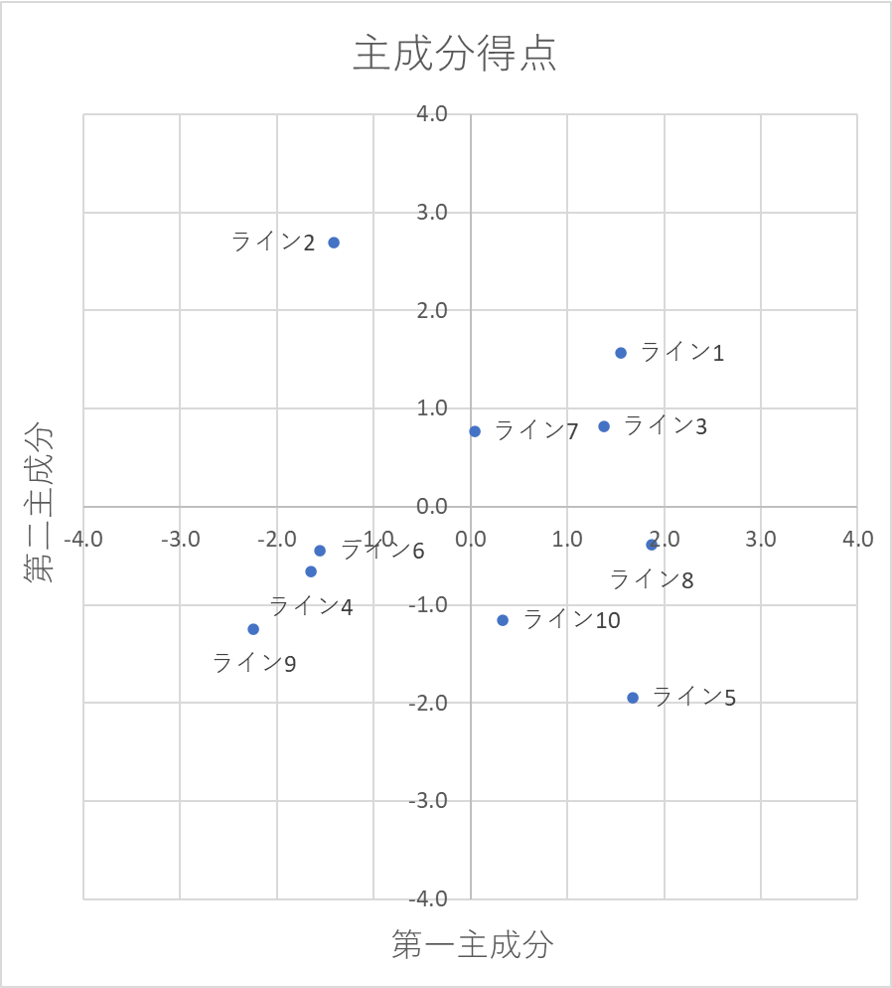
縦軸と横軸には、第一主成分と第二主成分をとり、各データを散布図でプロットします。
第一、第二・・とは、影響の大きい因子のことで、第一主成分の影響度が最も高いことを表しています。
これらの主成分は、マトリックス図の列の要素から選んだ変数ではなく、関連性の高い変数を組み合わせて新たに作り出した指標です。
ただ単に要素を絞るだけでは情報量が減るだけですが、新たに作り出した指標では、ばらつきを強調して表すことができるので、傾向の把握に効果的です。
先ほどの散布図を例に、何が読み取れるのか見てみましょう。
この散布図は、とある工場の製造ライン10本に対して、生産効率や安定性を指標に点数化して視覚化したものです。
第一主成分は「製造の安定性」、第二主成分は「生産能力」とネーミングしています。
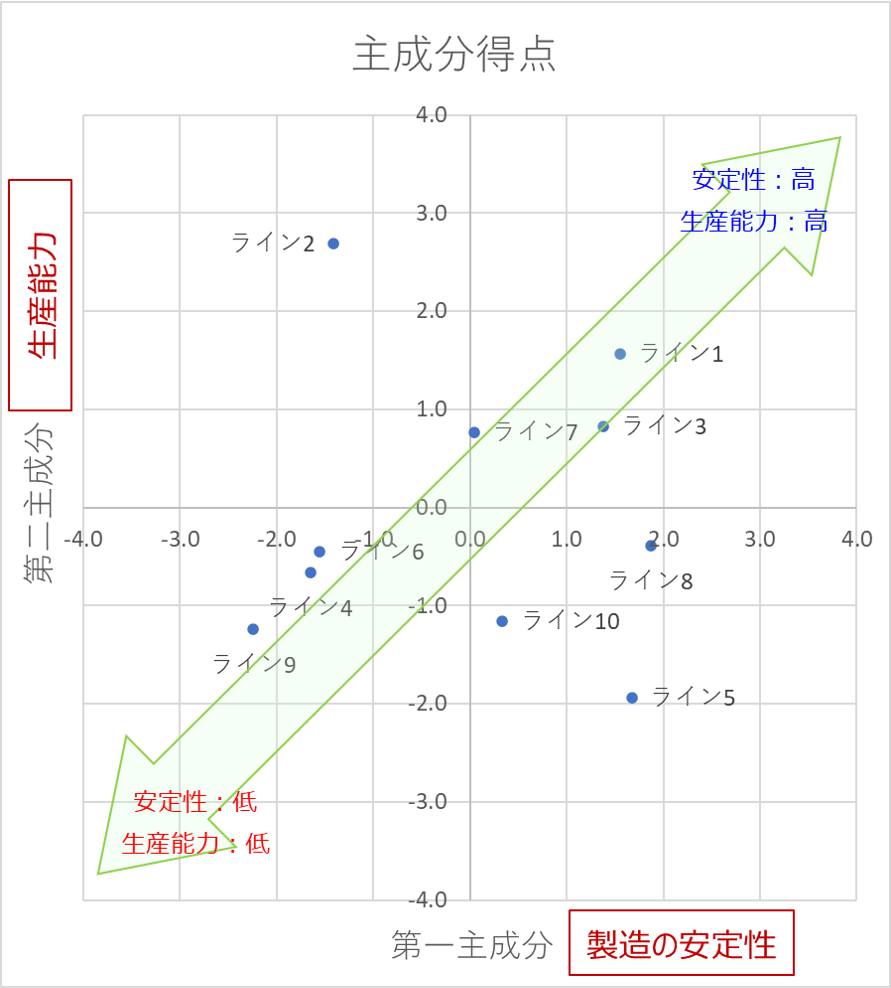
散布図から以下の傾向が把握できます。
ライン1:生産能力が高く、安定
ライン2:生産能力は高いが、不安定
ライン5:生産能力は低いが、安定
ライン9:生産能力が低く、不安定
このように、主成分の指標に対して、各データがどのように分布しているのか、視覚的に捉えやすいことが分かります。
一般的な事例としては、BMIのように身長と体重から算出した体格を表す指標や、学力試験などで理系科目や文系科目のように複数科目をまとめて表す指標などがあります。

指標をまとめたらスッキリしたね
主成分の意味
さて、先ほどから登場する「主成分」とは、どういう意味を持つものか説明します。
主成分分析の計算は、行列やベクトルを使う難解なイメージが強いですが、実は「データの傾向を把握しやすいように、座標系を取り直している」だけです。
例えば、変数を3つ(X・Y・Z軸)とした場合に、以下のように、元のデータが分布しているとします。
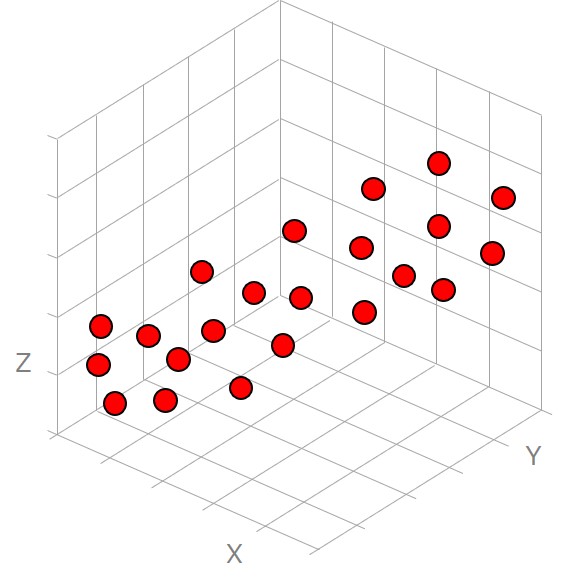
分布に相関が見られる場合、相関の最も大きい向きに第一主成分、その垂直方向に第二主成分をとります。
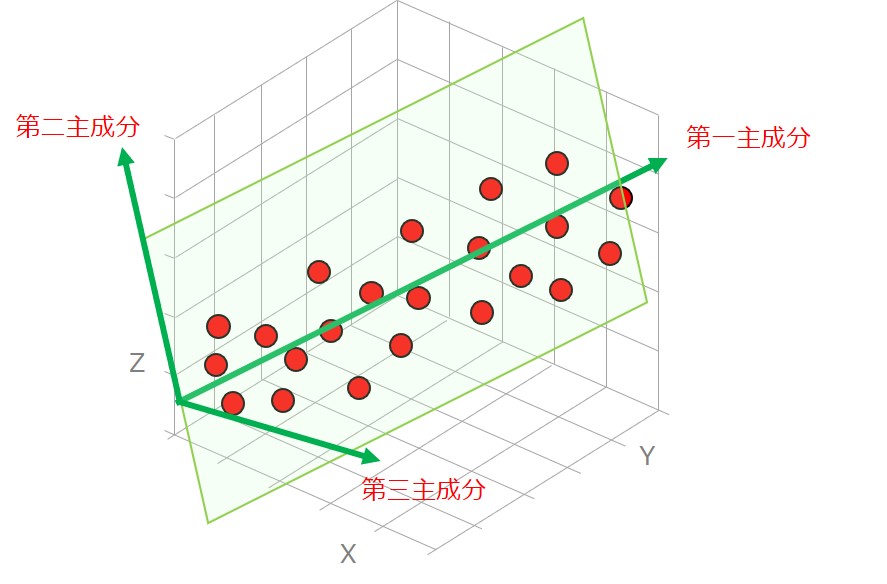
すると、第一主成分と第二主成分で構成する平面だけで、分布の傾向のほとんどを表すことができ、関連の低い第三主成分を省いても、支障がなくなります。
このように、関連性の強い向き(ベクトル)を計算で求めて座標軸を変換することが、主成分分析の考え方であり、後ほど、その手順を詳しく解説します。
なぜ使うの?
目的・用途・メリット
- 情報の縮約
多次元のデータでは、関係性を把握することが難しく、せっかく収集したデータを十分に活かしきれません。
できるだけ情報量を減らさずに要素を縮約して、問題と要因の関係をわかりやすく表すことができます。 - 指標の作成
関連性の高い変数を組み合わせて新たな指標を作り出すことができます。
この指標は、収集したデータの考察だけでなく、判定基準を的確に表すキーワードとして、これから先の活動に向けても活用することができます。 - 情報の共有
膨大な情報量を視覚化することで、第三者にも分かりやすく伝えることができます。
どうやって作るの?
散布図の作り方を解説します。
用語の説明
最初に用語を説明します。
数学的な意味合いは後ほど解説しますので、ここでは用語のイメージだけ掴んでいただければと思います。


いちどに用語覚えられないから、後で見返そう
手順
散布図を作る手順を解説します。
先ほども事例にあげた、とある工場の製造ライン10本に対して、生産効率や安定性を指標に点数化したデータをもとに解説していきます。
- テーマを決めて情報収集する
まず、目的を明確にして、元データとなる情報を収集しましょう。
指標を増やしすぎると、データ分析の時に大変ですし、反対に減らしすぎると情報量が不足するので、事前にしっかりと検討することが重要です。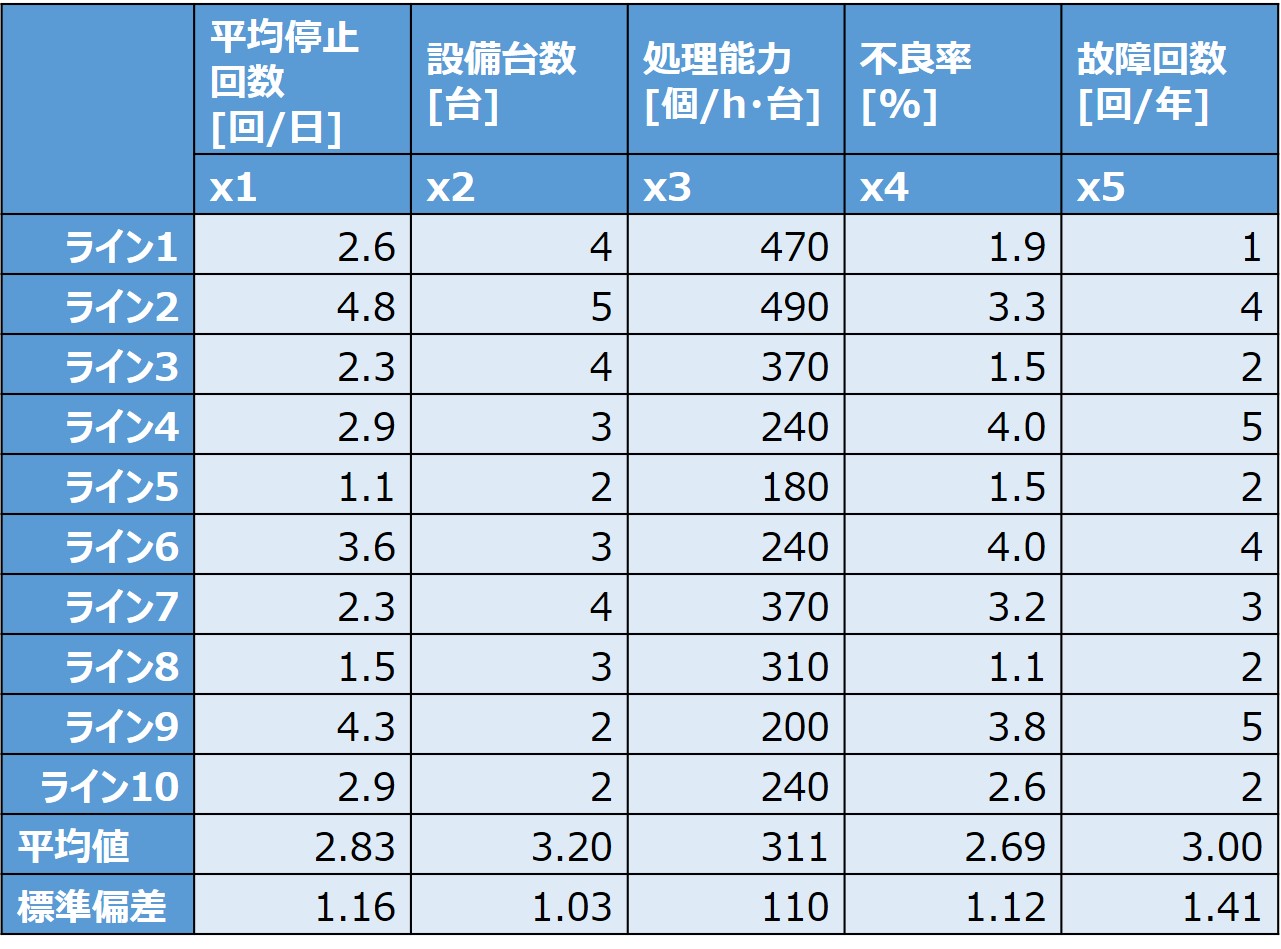
- データを標準化する
取得したデータの単位をそろえるため、以下の計算式で無次元化します。
標準化={(元データ)-(平均値)}÷標準偏差
数学的な意味では、平均値が0、標準偏差が1となるように換算します。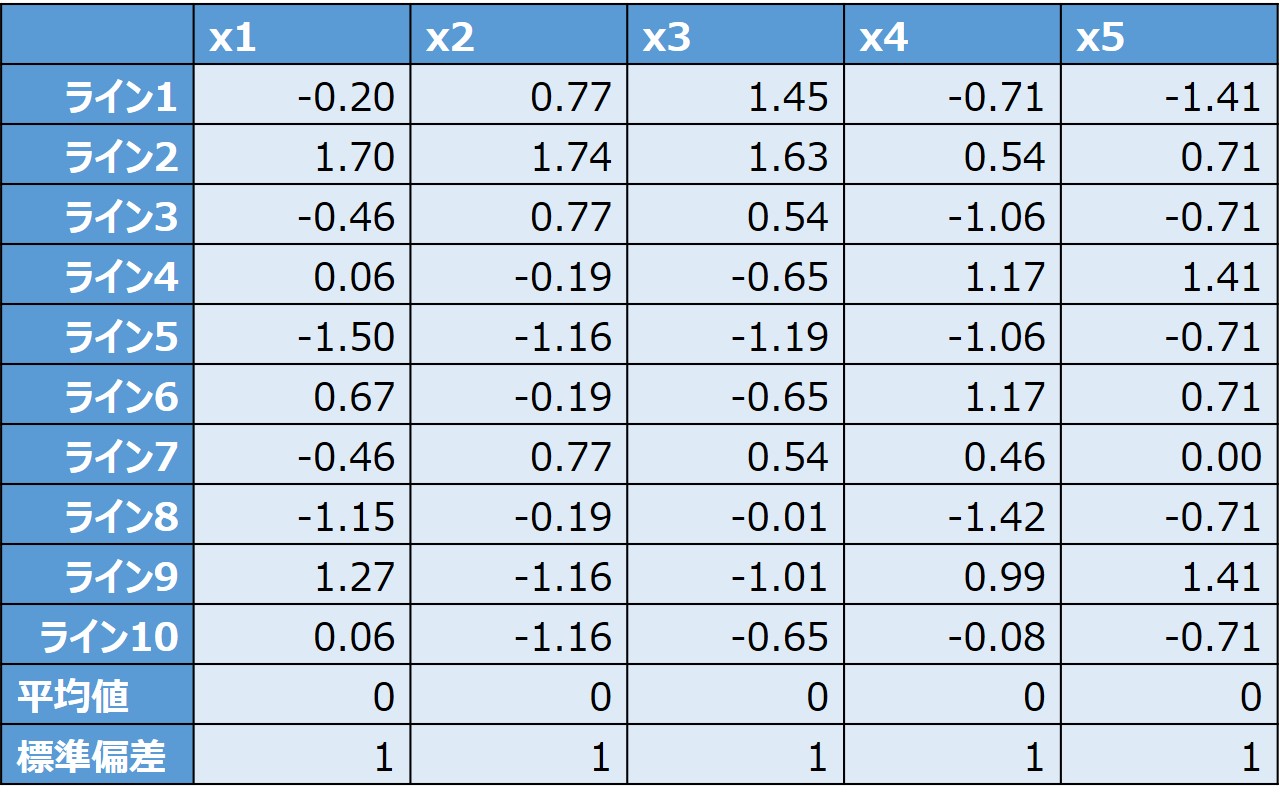
- 相関行列を求める
各変数の相関行列を求めます。
相関行列とは、変数どうしの相関係数を行と列に並べたものであり、対角の成分はすべて1となります。
対称行列なので、対角の半分だけを記載しています。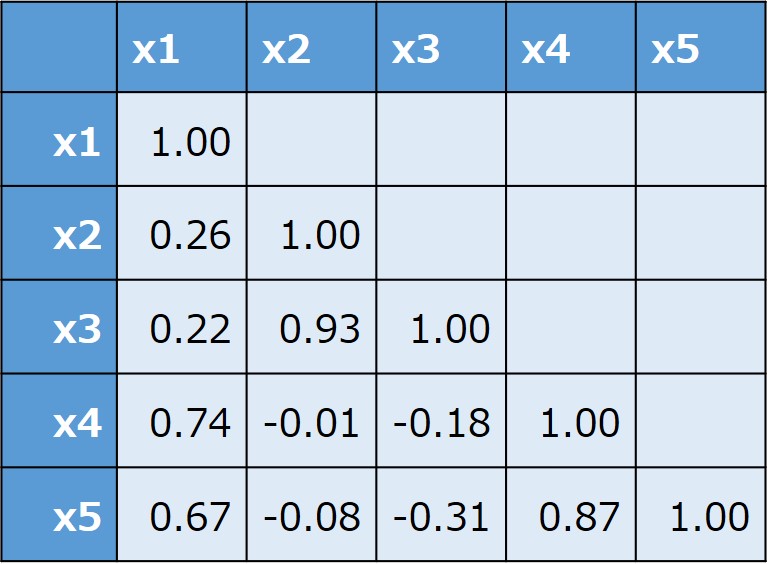
- 固有値・固有ベクトルを求める
相関行列の固有値をすべて求めます。数値の大きいものから、第一、第二主成分と対応づけられます。
さらに、各固有値について、固有ベクトルを求めます。表に記載のPCは、Principal Component(主成分)の略称です。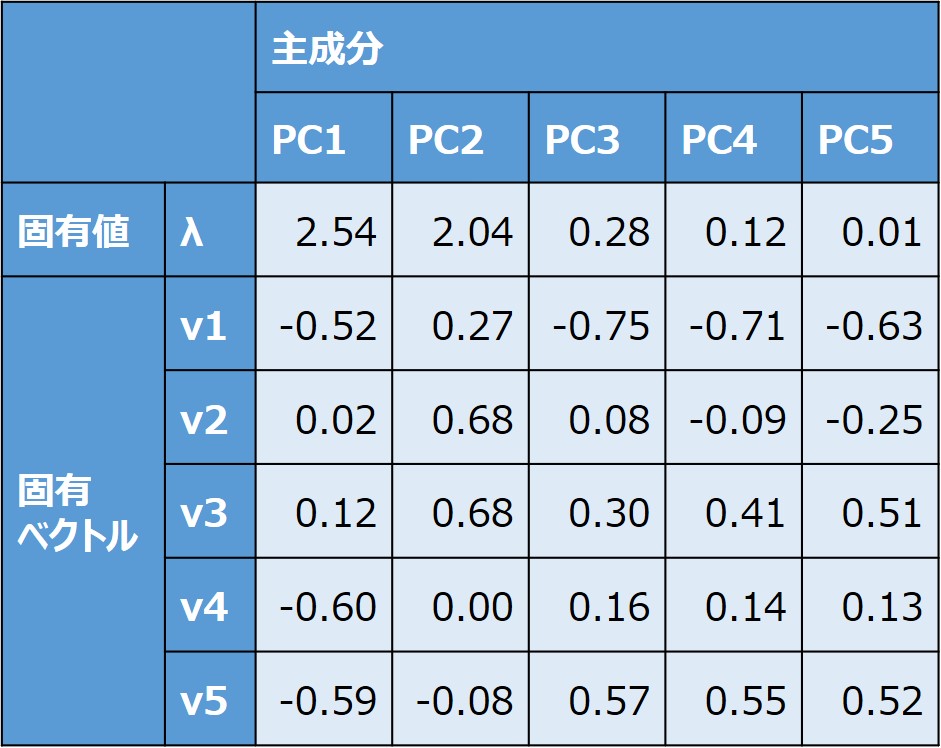
- 寄与率を見て主成分を選ぶ
固有値は、主成分の情報量の大きさを意味します。
つまり、固有値の大きさは寄与率の高さを表しており、以下の計算式で各固有値に対応する寄与率を算出できます。
寄与率=(固有値)÷(すべての固有値の合計)×100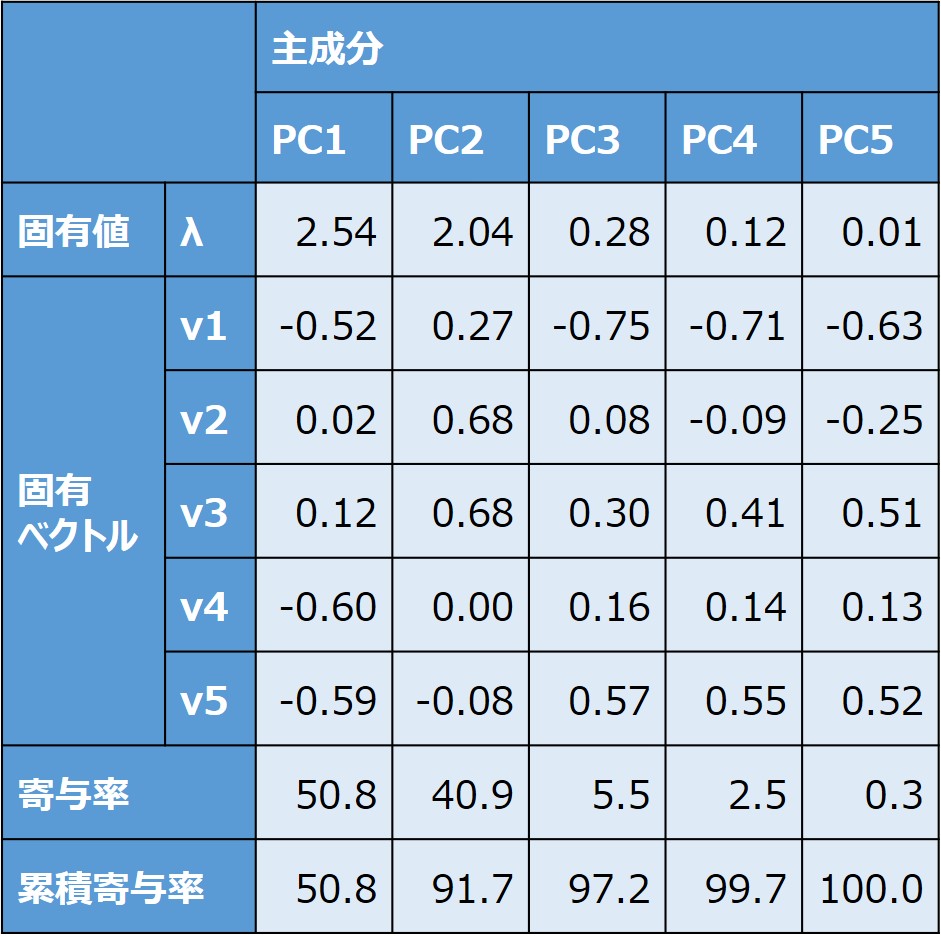
一般的に、第二主成分までを取ることが多いですが、累積寄与率があまりに低い(70%を下回る場合など)場合は、データの取り方を見直した方がよいかもしれません。 - 主成分に名前を付ける
主成分の特長を表すキーワードを考えて指標を作ります。
まず、以下の計算式で主成分負荷量を算出します。
主成分負荷量=(固有値の平方根)×(固有ベクトル)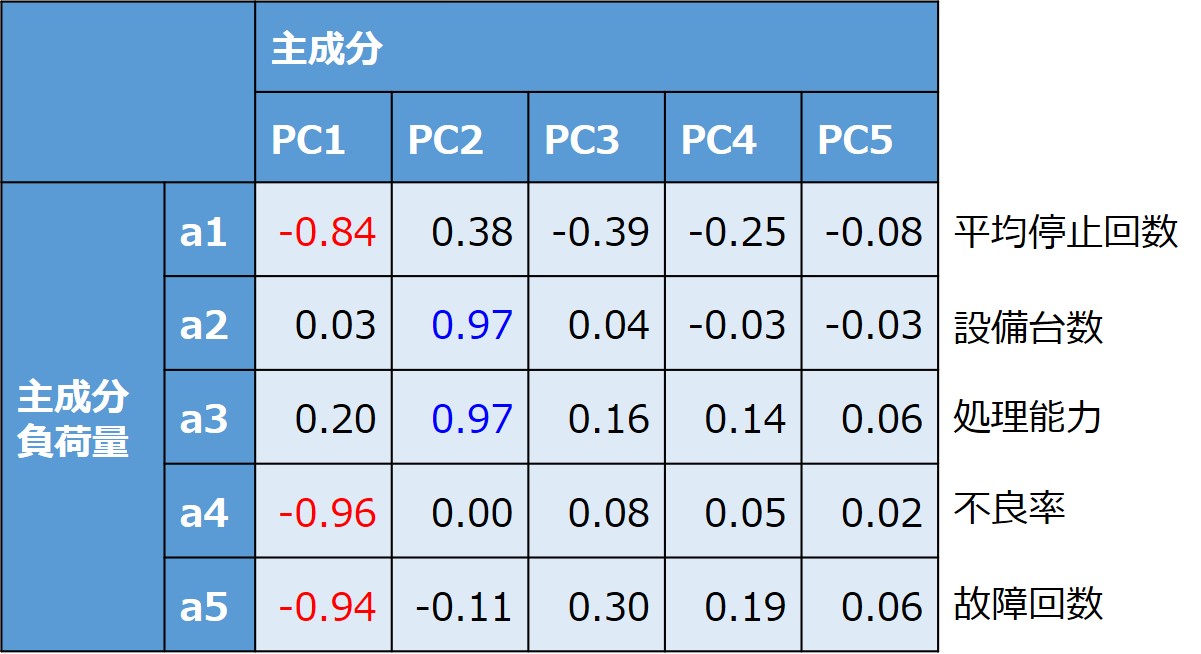
主成分負荷量は、次に計算する主成分得点と元の標準化データとの関係性の強さ(相関係数)を表す値のことで、-1~1の範囲の値を取り、絶対値が大きいほど関係が強いことを意味しています。
例えば、第一主成分に着目すると、「平均停止回数」「不良率」「故障回数」に対して、「-」の強い相関が出ています。
今回の事例では、これらの要素が小さい状態のことを「製造の安定性」と付けてみました。
同様に、「設備台数」「処理能力」が高いことを「生産能力」と表現しました。 - 主成分得点を散布図にする
元の標準化データに固有ベクトルをかけると、主成分得点を求めることができます。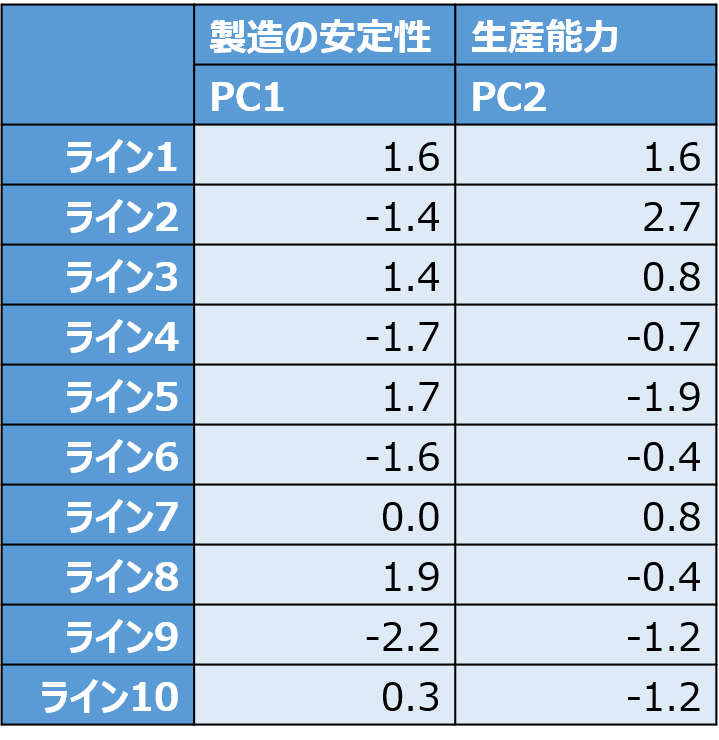
最後に散布図にすれば完成です!
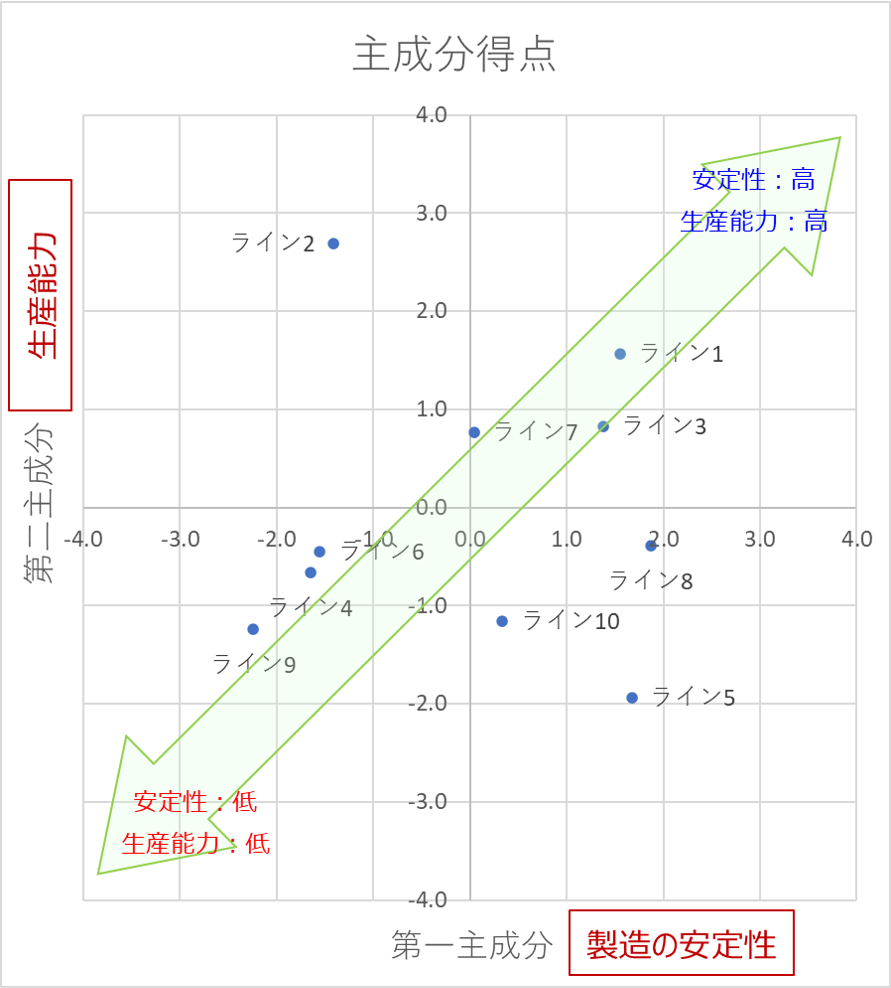
「製造の安定性」と「生産能力」の指標に対し、各ラインがどのような位置関係に分布しているのか、一目でわかりやすくなっています。

途中で計算間違えないよう注意しよう
計算の意味を知る
ここまで、できるだけ複雑な式を使わずに説明してきましたが、ここで少しだけ行列とベクトルの話をします。
固有値や固有ベクトルを計算することで、なぜ主成分を求めることができるのか、考え方のイメージを掴めるように解説します。
まず、固有値と固有ベクトルの定義をあらためて確認しましょう。
固有値とは、線型変換によって写されたあるベクトルが写される前のベクトルのスカラー倍になっているときの、そのスカラー量(拡大率)のことである。このベクトルで零ベクトルでないものを固有ベクトルという。
引用元:Wikipedia
固有値と固有ベクトルは、以下の式で定義されます。
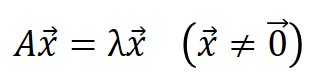
$A$は、とある$n$次元の正方行列で、$λ$が固有値、$x$が固有ベクトルを表します。
マトリックスデータ解析法では、$A$が相関行列のことで、$A$に対する$λ$と$x$を算出しています。
固有値・固有ベクトルを求める意味
固有ベクトルには以下の特長があります。
①:ベクトルの向きが変わらない
ひとつ目のポイントは、行列$A$と固有ベクトルをかけても、ベクトルの向きが変わらないことです。
行列$A$は、元のデータの相関関係を表したもので、つまり元のデータの分布状態そのものを表しています。
「ベクトルの向きが同じ=データの関係性が崩れない」ことを活かしています。
反対にベクトルの向きが変わると、データの位置関係が崩れてしまうので、元のデータと同じものではなくなってしまいます。
②:スカラー倍に変換できる
ふたつ目のポイントは、行列$A$に固有ベクトルをかけると、スカラー倍に変換できることです。
行と列の成分をスカラーに変換するということは、大きさを一次元で表すことになり、すなわちデータのばらつきを最大に表すことができます。
つまり、固有ベクトルをかけることで、データの位置関係を崩さずに、ばらつきを最大に表すことができるのです。
これがまさに座標軸の変換を意味しています。
ちなみに、相関行列の固有ベクトルの大きさは1となるので、この係数成分として固有値が定義されます。
固有値の用語説明で、主成分が持っている情報量の大きさを示す指標と表現したのは、こういった計算式に基づくものです。
主成分負荷量の計算の意味
主成分負荷量は、以下の計算式で求めるとお伝えしました。
主成分負荷量=(固有値の平方根)×(固有ベクトル)
固有ベクトルをかけることで、座標軸を変換できることは先ほど説明した通りです。
では、固有値の平方根をとる意味は何でしょうか?
固有値は、ばらつきを表す指標で、数学的には「固有値の合計は、元の変数の分散の合計に等しい」関係性が成り立っています。
分散は、それぞれのデータと平均値との差分の二乗で算出できる成分です。
つまり、分散の平方根をとることで、次元を合わせているのです。

意味を理解していれば、手順も間違えないね
注意点
- 情報の縮約であることを認識する
- 統計量の取り扱いに注意する
- きちんと理屈を考える
- 情報の縮約であることを認識する
マトリックスデータ解析法では、膨大な情報量のデータをわかりやすくするため、座標軸を変換して次元を落としています。
平面図にすることで、関連性の低い成分の情報は見えなくなってしまうので、元データの情報がすべて残っているわけではないことを理解しておきましょう。 - 統計量の取り扱いに注意する
数値として結果を出せるので、比較しやすく分かりやすいですが、ひとつ計算を間違えると、当然、計算結果も違うものになります。
計算方法が複雑なので、途中段階で間違いがないか、きちんと精度を確認しながら進めましょう。 - きちんと理屈を考える
計算結果から示された傾向をそのまま鵜呑みにせず、因果関係が妥当なものか、きちんと理屈を考えて整理しましょう。
余談
Excelを使う場合、固有値や固有ベクトルは関数ひとつで算出することができず、残念ながらアドインにも含まれていません。
Excelでの計算手順については、別の記事で紹介していますので、合わせて参考にしていただければと思います。
こてつ経験談
意気込んで集めてみたものの
この記事で例に挙げた「製造ラインの総合評価」という題材は、変数の取り方やまとめ方など、私が若手時代に実践したものベースにしています。
当時、評価指標として何を変数にするか検討したのですが、前例として決まった項目もなく、悩ましいものでした。
ひとまず、変数は多い方が情報量も増えるし良いだろう、と安易な発想で、思いつくパラメータを変数に取り、製造ラインのデータ収集を始めました。
収集に膨大な労力を費やしつつ、何とかすべてのデータを集めるところまでは良かったのですが、いざ、まとめの段階に入ると、手が止まってしまいます。
それもそのはず、情報量が多すぎて何も入ってこない、整理するにも何から手を付けたらよいのやら・・と、せっかくのデータを活かしきれませんでした。

理解力とのバランス
情報に埋もれて頭がパンクしたところで、無理にすべての情報を残すことを諦め、情報を縮約することにしました。
といっても、単に変数を減らすだけでは、自分の労力が報われません。
そこで、学生時代に統計学で聞きかじった主成分分析をやってみることにしたのです。
最初は、計算式の意味も理解できていないまま、手順通りに進めただけですが、それでもスッキリと整理された結果を見て感動を覚えた記憶があります。
「情報」は自分が吸収する、あるいは他人に伝えることが一番の目的であって、その重要性を認識する良い機会でした。
まず、自分が吸収するには、自分の理解力に最も適した形で表現することが大切で、それは多次元でも3次元でもなく、2次元でマッピングすることでした。
これは私に限らず、多くの人にとって平面図で直感的に理解することが最も効率的と思います。
理解力と得られる情報量のバランスを考えた結果、主成分分析にたどり着いたというお話でした。
まとめ
- マトリックスデータ解析法
⇒できるだけ元のデータの情報を残しつつ、要素を縮約して二次元の平面図に表し、問題と要因の関係をわかりやすく示す手法のこと(主成分分析)。 - 目的・用途
⇒情報の縮約、指標の作成、情報共有 - 計算の意味
⇒固有値と固有ベクトルを用いることで、データの位置関係を崩さずに、ばらつきを最大に表している(座標軸の変換)。 - 注意点
⇒①:情報の縮約であることを認識する
②:統計量の取り扱いに注意する
③:きちんと理屈を考える
たくさんのデータを集めても、それを活かしきれなければ、複雑になって難しくなるだけです。
関係性の高い成分を抽出して他を見ないようにすることで、スッキリと整理でき、理解が促進されます。
情報の取捨選択に有効なツールですので、ぜひ活用してみてください。




コメント