この記事では、マトリックスデータ解析法の散布図をExcelで作る方法を解説します。
数値計算に必要な固有値や固有ベクトルはExcelの関数ひとつで算出することができず、残念ながらアドインにも含まれていません。
専用ソフトやEcxelのマクロを使えば算出できますが、そのような手段を使えない方に向けて、Excelの関数を使って求める方法を解説しています。
マトリックスデータ解析法の計算の意味や使い方は、別の記事で詳しく紹介していますので、合わせて参考にしていただければと思います。


固有値や固有ベクトルを使う意味を知りたい人は別の記事を先に読んでね
マトリックスデータ解析法とは?
- マトリックスデータ解析法
⇒できるだけ元のデータの情報を残しつつ、要素を縮約して二次元の平面図に表し、問題と要因の関係をわかりやすく示す手法のこと(主成分分析)。 - 目的・用途
⇒情報の縮約、指標の作成、情報共有 - 計算の意味
⇒固有値と固有ベクトルを用いることで、データの位置関係を崩さずに、ばらつきを最大に表している(座標軸の変換)。
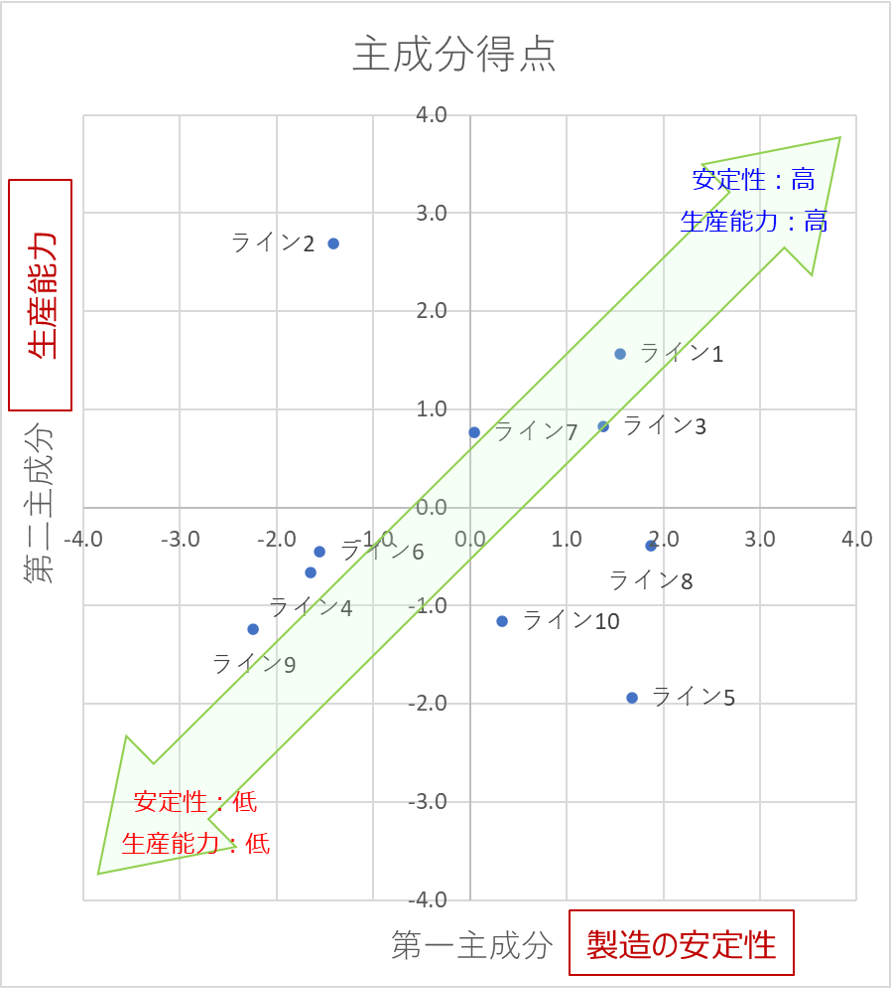
マトリックスデータ解析法で作成する散布図のイメージを以下に示します。
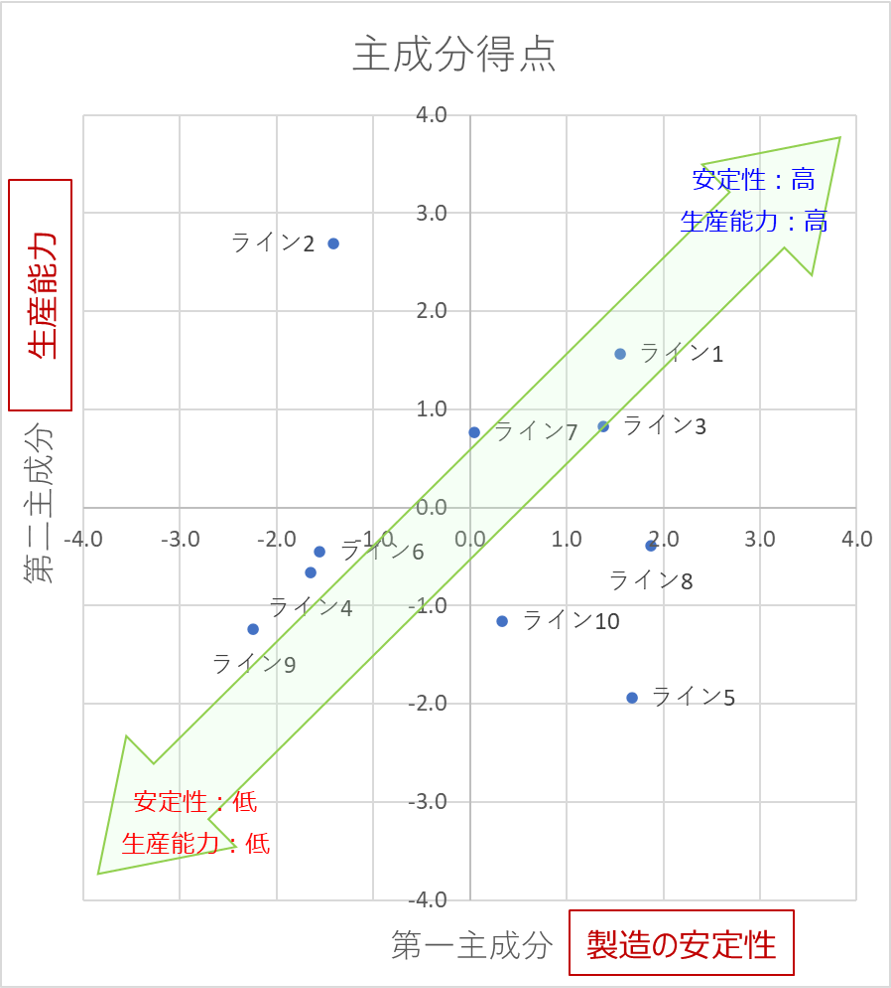
縦軸と横軸には、第一主成分と第二主成分をとり、各データを散布図でプロットします。
第一、第二・・とは、影響の大きい因子のことで、第一主成分の影響度が最も高くなります。
これらの主成分は、マトリックス図の列の要素から選んだ変数ではなく、関連性の高い変数を組み合わせて新たに作り出した指標です。
数学的な意味としては、固有値と固有ベクトルを用いることで、データの位置関係を崩さずに、ばらつきを最大に表した指標のことです。
用語の説明

Excelでの作り方
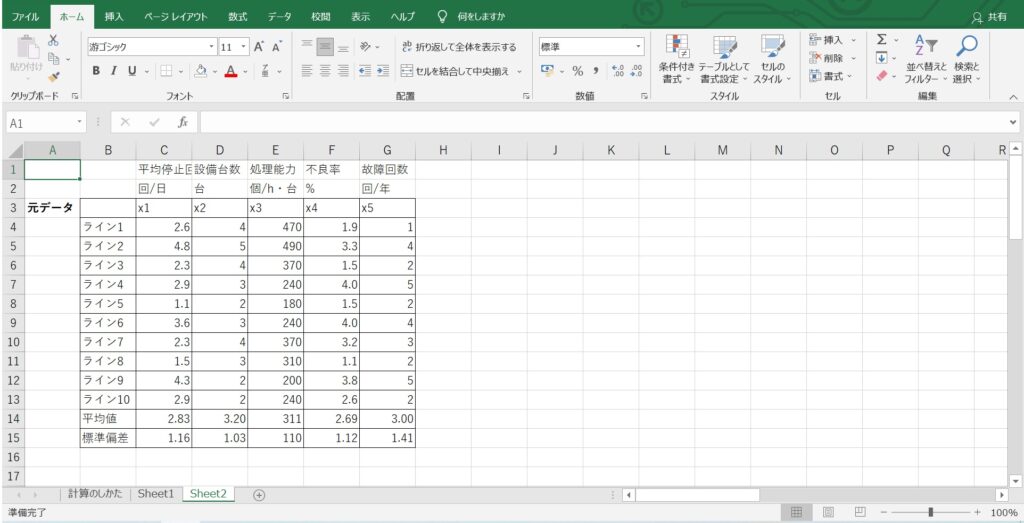
マトリックスデータ解析法の記事でも紹介した、とある工場の製造ライン10本に対して、生産効率や安定性を指標に点数化したデータを題材に解説していきます。
アドインの設定
データ収集や編集の前に、Excelの設定をしておきましょう。
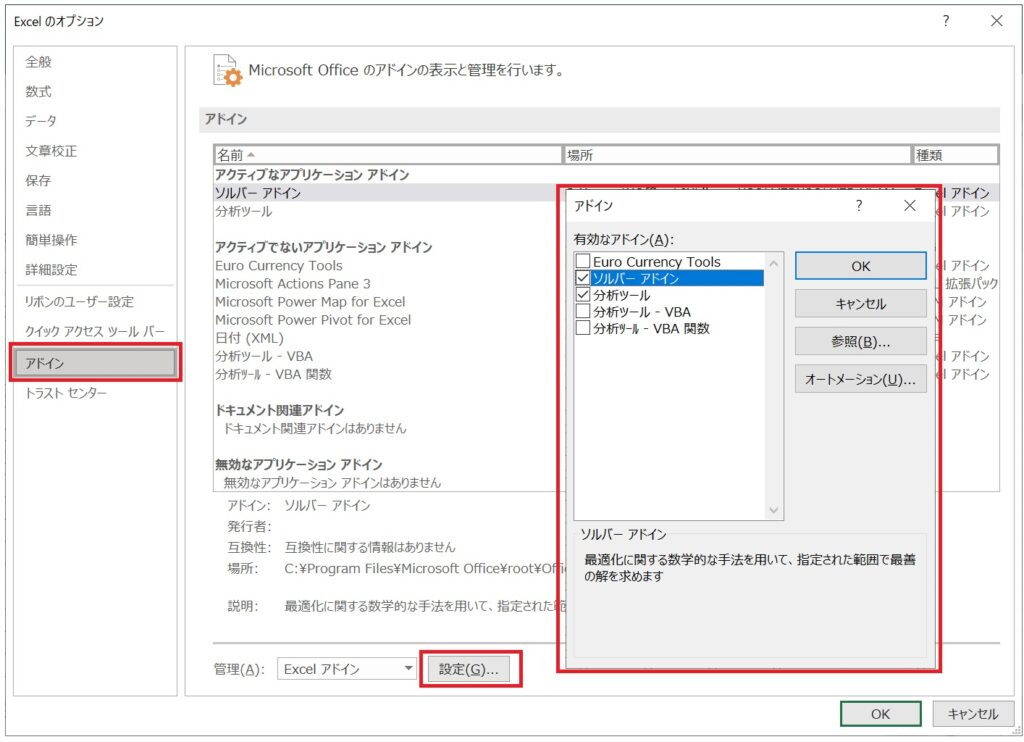
固有ベクトルの計算にソルバーというアドインを使用しますので、まずはアドインを設定します。
「ファイル」→「その他」→「オプション」を選択します。
「アドイン」→「設定」を指定し、「ソルバーアドイン」にチェックを入れて、有効化します。

有効化を忘れると、リボンに表示されないから気を付けよう
情報収集
まず、目的を明確にして、元データとなる情報を収集しましょう。
指標を増やしすぎると、データ分析の時に大変ですし、反対に減らしすぎると情報量が不足するので、事前にしっかりと検討することが重要です。
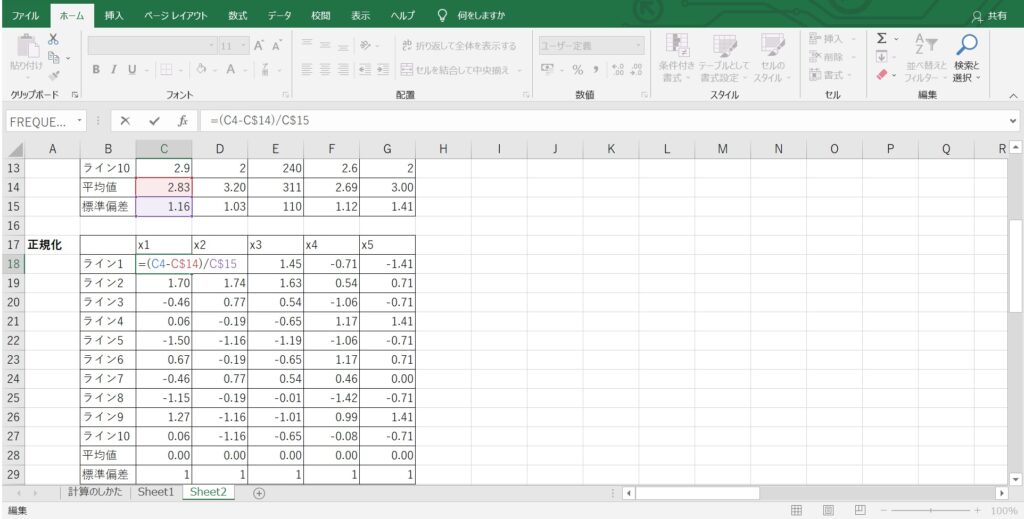
データの標準化
取得したデータの単位をそろえるため、以下の計算式で無次元化します。
標準化={(元データ)-(平均値)}÷標準偏差
数学的な意味では、平均値が0、標準偏差が1となるように換算します。
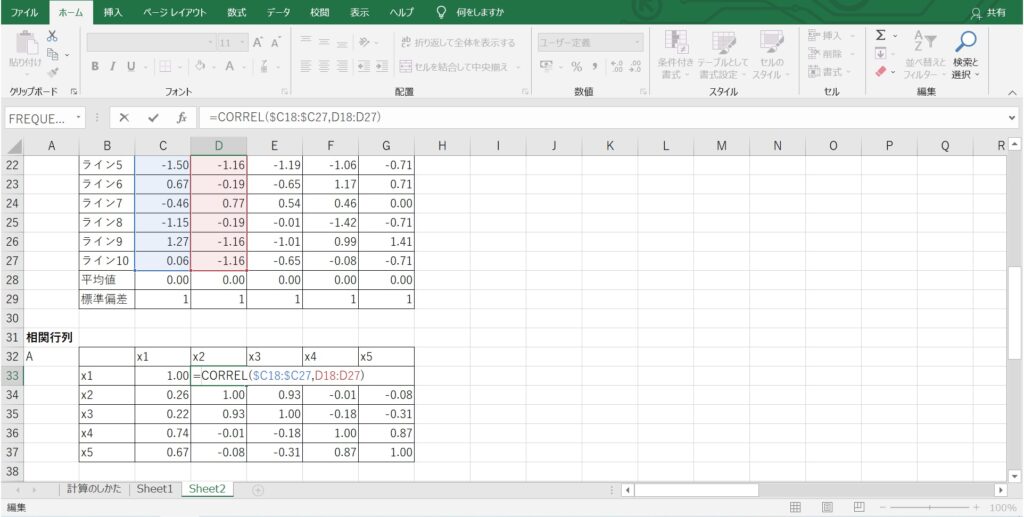
相関行列の算出
各変数の相関行列を求めます。
相関行列とは、変数どうしの相関係数を行と列に並べたものであり、対角の成分はすべて1となります。
相関係数の算出には、CORREL関数を使用します。
対象の変数列を2つ設定し、相関係数の行列を作成します。
固有値の算出
固有値と固有ベクトルは、以下の式で定義されます。
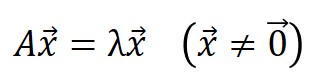
$A$は、とある$n$次元の正方行列で、$λ$が固有値、$x$が固有ベクトルを表します。
$A$が相関行列のことで、$A$に対する$λ$と$x$を算出します。
まずは、固有値を算出しましょう。
先ほどの式を以下のように変換します。
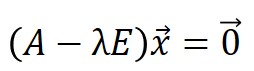
$E$は単位行列を表し、対角成分が1、その他は0で構成される行列です。
$x$が零ベクトルでない場合、上式は次のように変換されます。
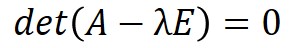
detは行列式を表します。
行列式とは、例えば2次正方行列の場合、以下のように計算します。
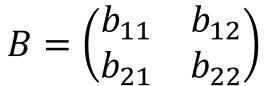
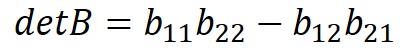
つまり、$A-λE$の行列式を解くことが固有値$λ$を求めることになります。
第一主成分のλを求める
$λ$を求めるには、Excelのゴールシーク機能を使います。
ゴールシークとは簡単にいうと逆算機能で、例えば、$det(A-λE)=0$を満たす$λ$を逆算で求めることができます。
実際に、ゴールシーク機能で$λ$を求めてみます。
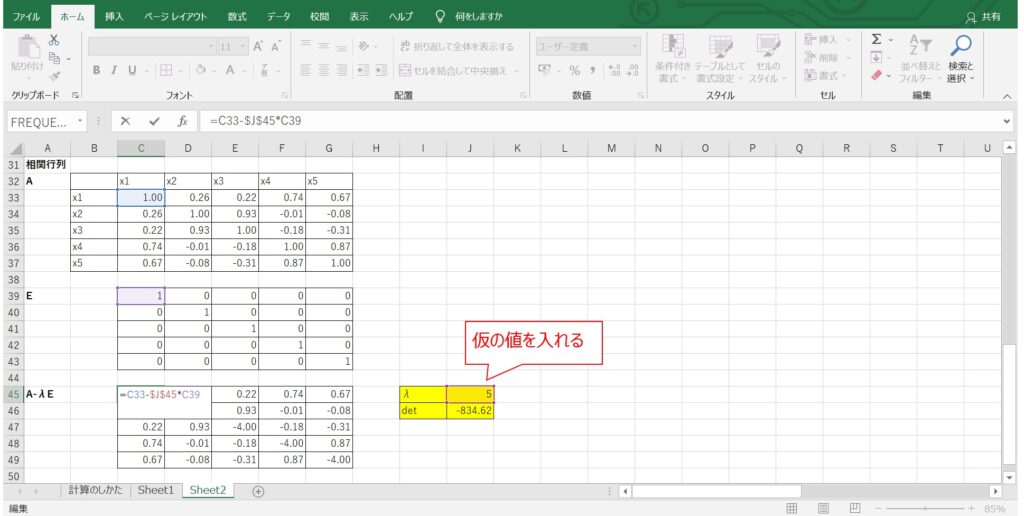
そこで、まず$A-λE$を計算します。未知数の$λ$には、仮の値を入れておきます。
ちなみに、数学的には「固有値の合計は、元の変数の分散の合計に等しい」という関係性があります。
各変数の標準偏差が1なので、その二乗の分散も1です。すなわち、今回のように変数が5個の場合、固有値は5以下となります。
そのため、$λ$の仮の値には、まず最大値の5を入れることをお勧めします。
この後、すべての$λ$を求めるにあたって、仮の値を何にするかによって、見つける速さが全然変わります。
さらに、$A-λE$の行列式detを計算します。
Excelでは、MDETERM関数を使用すると、行列式を計算することができます。
行と列をいちどに選択するには、データ範囲を指定して、「ctrl+shift+Enter」を押します。
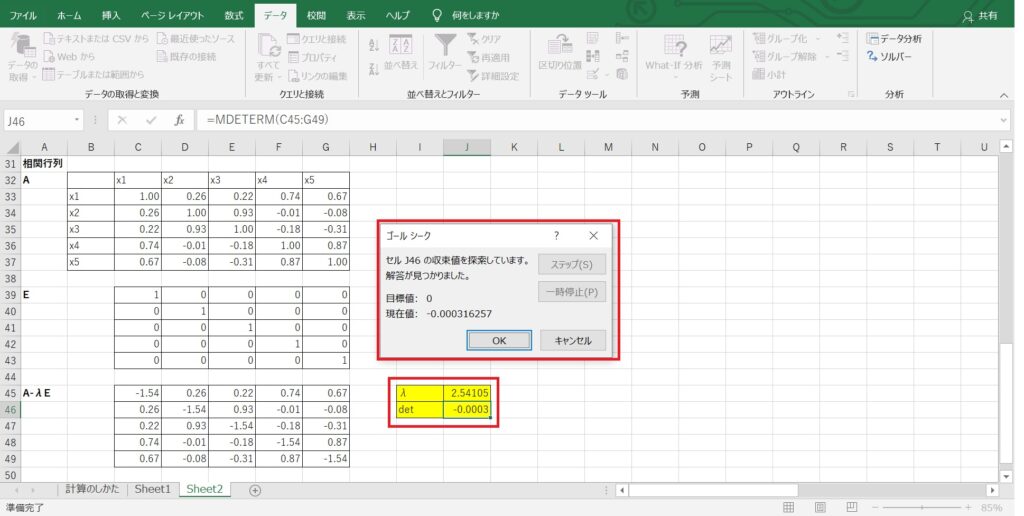
つづいて、「データ」「What-If分析」「ゴールシーク」を選択し、以下の条件を指定します。
数式入力セル:det
目標値:0
変化させるセル:$λ$
すると、以下のように逆算して$λ$を求めることができました。
ゴールシーク機能では、最初に仮決めした$λ$の値から、徐々に値を変化させて目標値に収束する解を見つけていきます。
仮の値で最大値の5を設定したのは、最初に収束する値が固有値の最大値、すなわち第一主成分を見つけるためです。
第$n$主成分の$λ$を求める
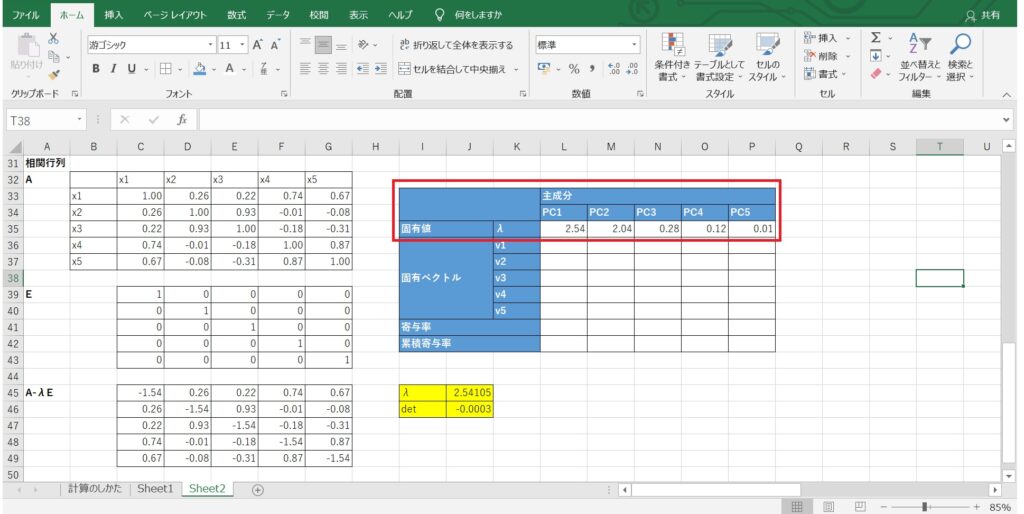
同様に残りの固有値を見つけていきます。
重複解を含めると、全部で変数の数(今回は5個)の解があります。
先ほどは$λ$の最大値を見つけたので、今度は最小値を見つけるため、仮の値に0を入れて計算します。
最大値と最小値が出たら、残りの3つはその間の適当な値を仮に設定し、見つけ出したものから順に書き出していきます。

ぜんぶ足したら変数の数になるか確認しよう
固有ベクトルの算出
固有値をすべて求められたら、次はそれぞれの固有値に対応する固有ベクトルを求めます。
固有ベクトルを計算する際にも同様に逆算を行いますが、ベクトル成分を変化させる必要があるので、ソルバー機能を使います。
基本的にやっていることは同じですが、ゴールシークは変化させる成分が1つに対し、ソルバーでは複数成分を同時に変化させることができます。
また、ソルバー機能では、制約条件も設定することができるので、固有ベクトルを算出するには、この機能が必須です。
計算セルの準備
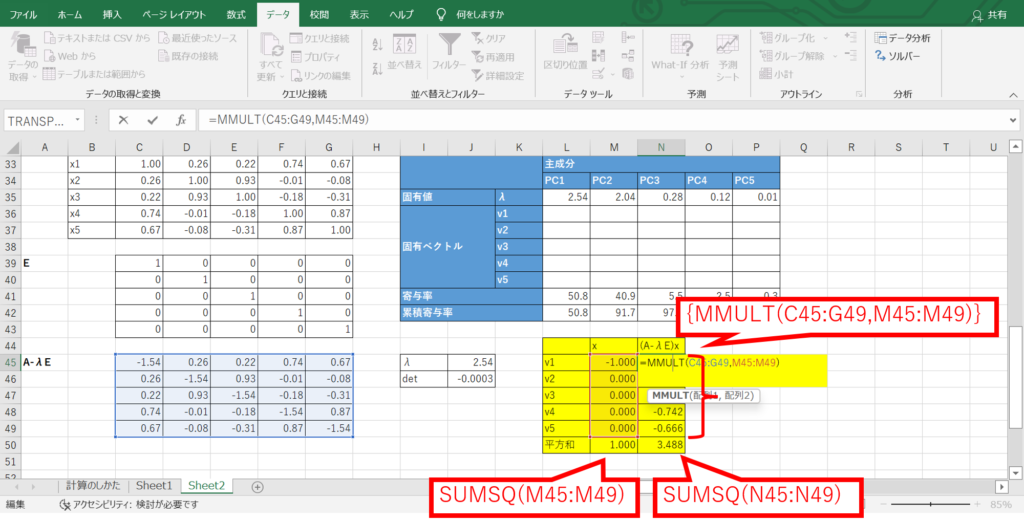
まず、固有ベクトル$x$の仮の値を入れるセルと、$(A-λE)x$を計算したセルを準備します。
$(A-λE)x$の算出には、行列の積を計算するMMULT関数を使用します。
行と列をいちどに選択するには、データ範囲を指定して、「ctrl+shift+Enter」を押します。
また、固有ベクトルの制約条件として二乗和を設定します。
相関行列に対する固有ベクトルの大きさは1なので、固有ベクトルの各成分の二乗和は1になります。
この後、ソルバーで二乗和が1の制約条件を設定します。
また、$(A-λE)x$の各成分の二乗和も計算しておきます。
「各成分がすべて0=二乗和が0」と同じ意味ですので、ソルバーに設定する目標値を簡単にするために使用します。
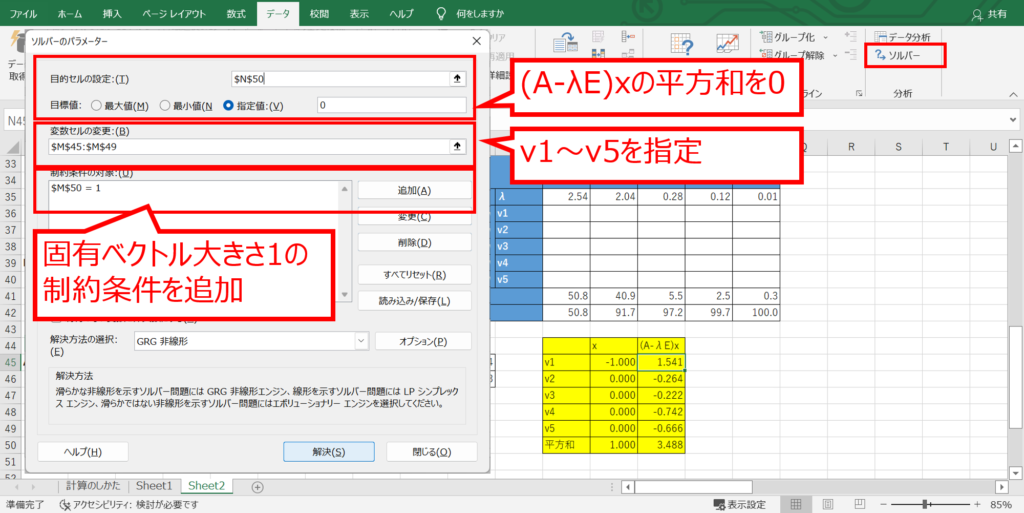
ソルバーで固有ベクトルを求める
「データ」「ソルバー」を選択し、以下のパラメータを設定します。
目的セルの設定:$(A-λE)x$の二乗和
指定値:0
変数セルの変更:固有ベクトル($v1~v5$)
制約条件:固有ベクトルの大きさが1
すべてのパラメータを設定できたら、「解決」を押します。
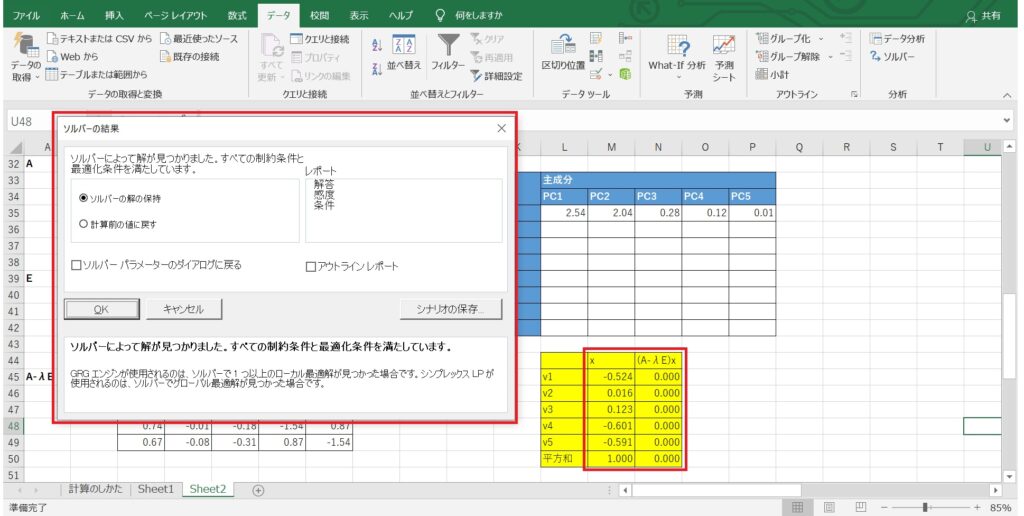
すると以下のように、「解が見つかりました」と表示されれば、計算完了です。
この時、$x$の二乗和が1になっていることと、$(A-λE)x$の成分がすべてゼロになっていることを確認しましょう。
うまく解が出ない場合は、初期の仮設定の値が適切でないために、解が収束していない可能性があります。設定をもういちど見直してリトライしましょう。
例えば、初期値として$v1~v5$を全て0にすると、最初から収束条件の中に入ってしまっていて、計算が上手く回らない事例が確認されています。

操作に慣れたら、サクサクできそう
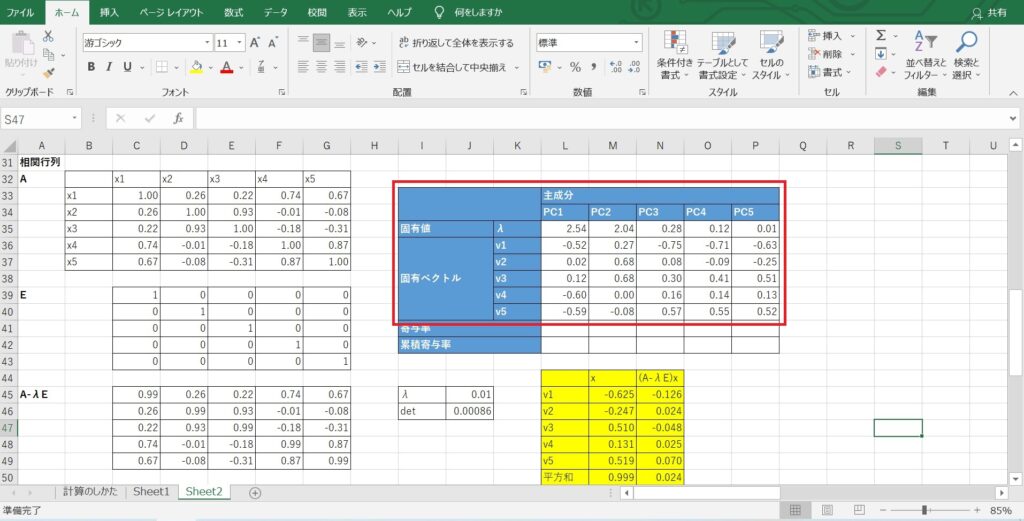
寄与率から主成分を選定
固有値は、主成分の情報量の大きさを意味します。
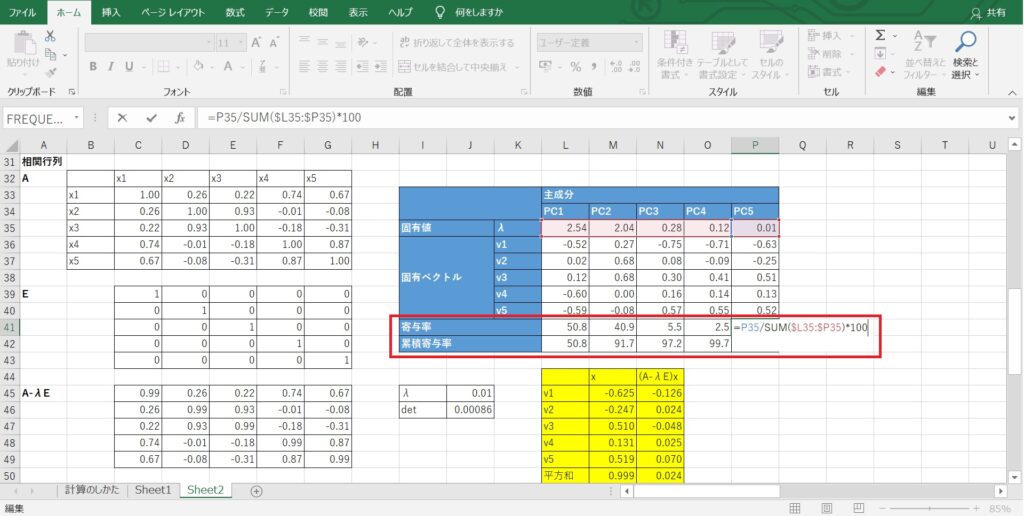
つまり、固有値の大きさは寄与率の高さを表しており、以下の計算式で各固有値に対応する寄与率を算出できます。
寄与率=(固有値)÷(すべての固有値の合計)×100
マトリックスデータ解析法では、第二主成分までを取ることが多いですが、累積寄与率があまりに低い(70%を下回る場合など)場合は、データの取り方を見直した方がよいかもしれません。
主成分のネーミング
主成分の特長を表すキーワードを考えて指標を作ります。
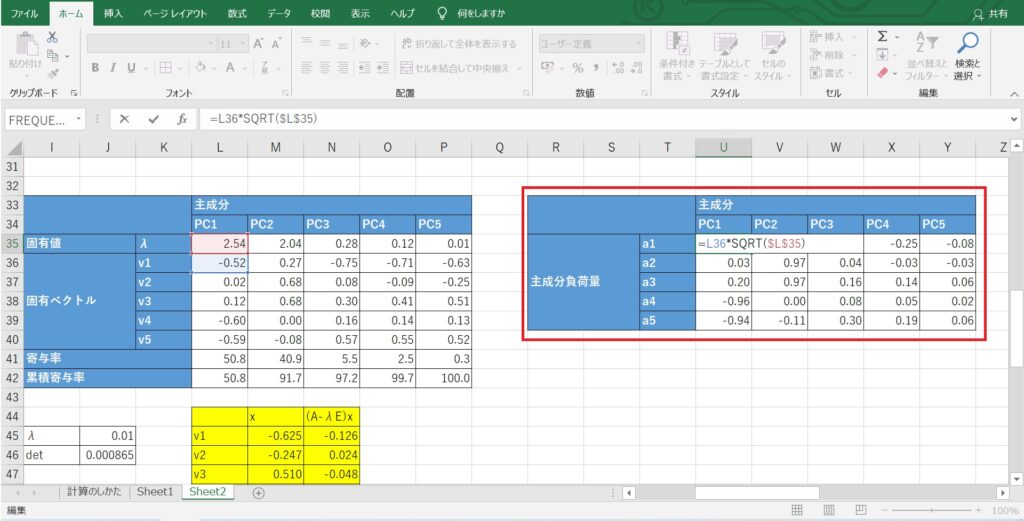
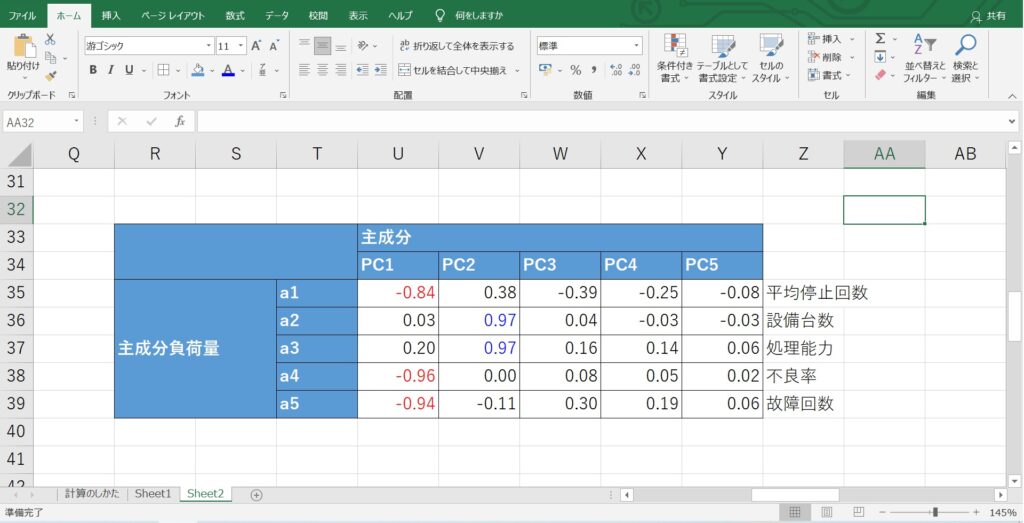
まず、以下の計算式で主成分負荷量を算出します。
主成分負荷量=(固有値の平方根)×(固有ベクトル)
例えば、第一主成分に着目すると、「平均停止回数」「不良率」「故障回数」に対して、「-」の強い相関が出ています。
今回の事例では、これらの要素が小さい状態のことを「製造の安定性」と付けてみました。
同様に、「設備台数」「処理能力」が高いことを「生産能力」と表現しました。
散布図の作成
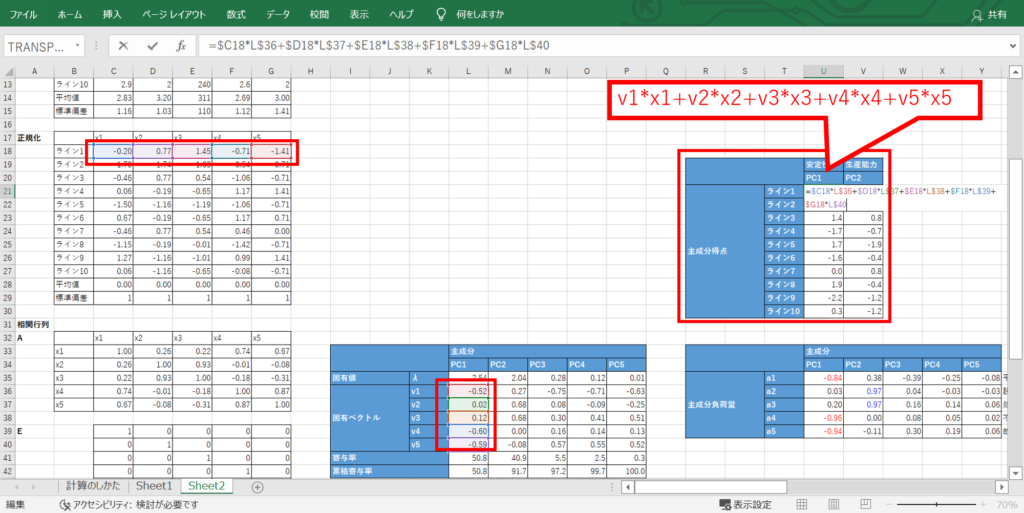
元の標準化データに固有ベクトルをかけると、主成分得点を求めることができます。
最後に散布図にすれば完成です!
固有ベクトル計算の小技
ソルバーの収束条件
ソルバーで固有ベクトルを求める際に、収束条件を厳しくしすぎると解が得られない場合があります。
これは固有ベクトルの初期値が適切でない(全て0にした場合など)他、収束判定値を厳しくしすぎた場合に、いつまでも条件内に収まらず、解が見つからないまま計算が途中で終了してしまいます。
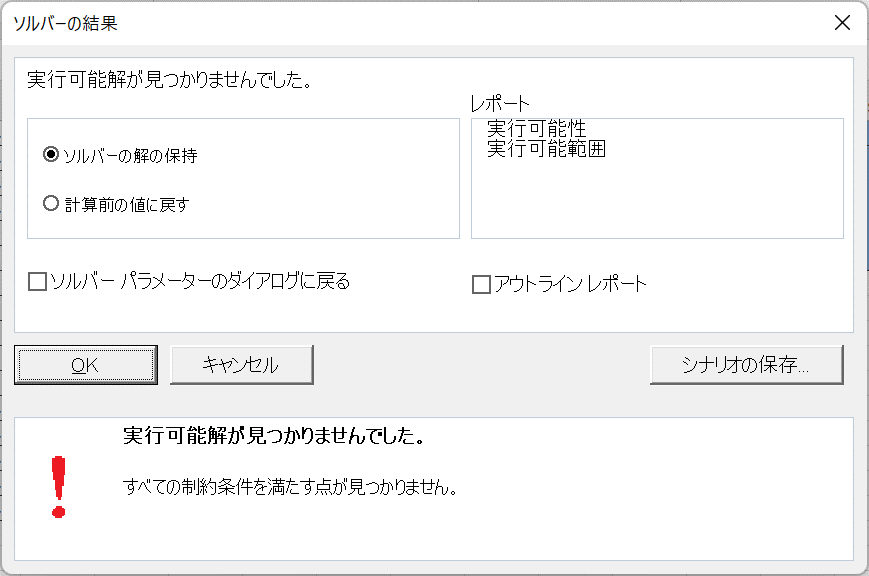
このような場合には、ソルバーの設定として「オプション」を選択し、制約条件の精度を適度に緩くすると解消します。
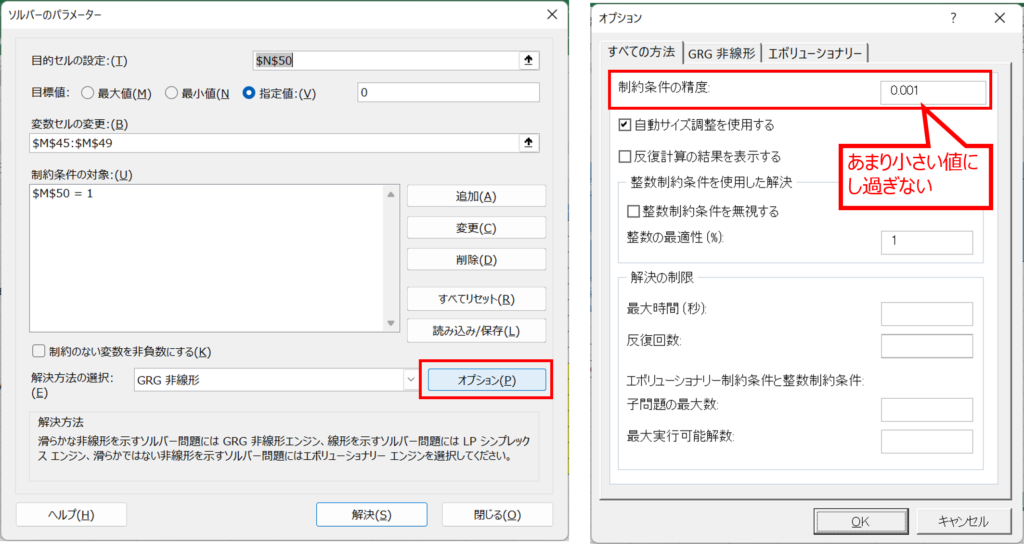
もちろん、計算結果の精度に影響のない範囲が前提ですが、どうしても計算が回らない場合は試してみてください。
固有ベクトルの初期値設定
固有ベクトルの初期値設定の正負を変えると、ソルバーで得られる解のベクトルの正負が変わる場合があります。
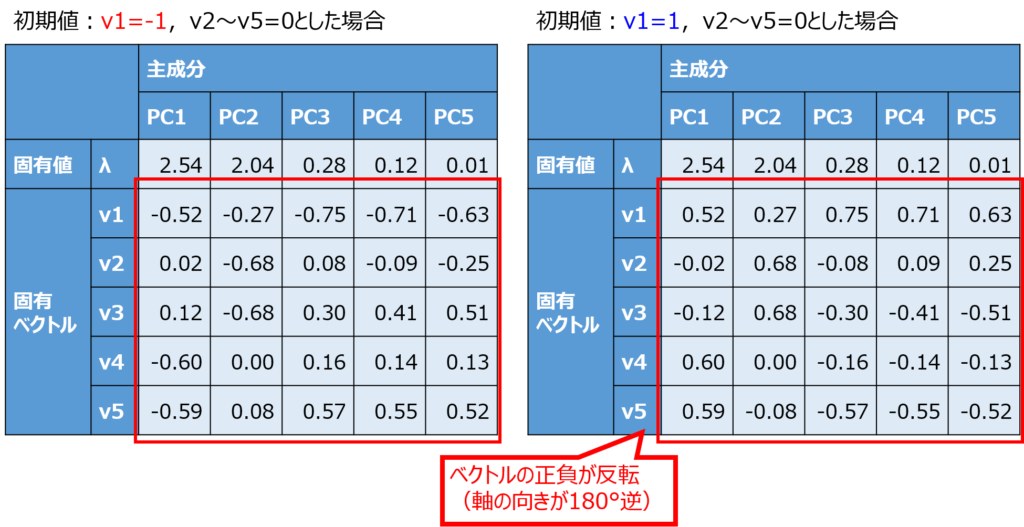
これはソルバー計算の反復機能の性質で、初期値の値から徐々に変化させて計算を繰り返すので、最初に収束するベクトルの向きが正負逆転するのです。
この場合、もちろん主成分得点にも正負の結果が反映されます(値が正負反転)。
ただし、主成分分析では元データのばらつきを大きく表す新しい座標軸に変換することが目的なので、座標変換した主成分得点の正負は解析者が後に意味付けをすれば問題ないことです。
例えば次のように第二主成分の正負を反転させると上下反転した二次元マップが得られます。
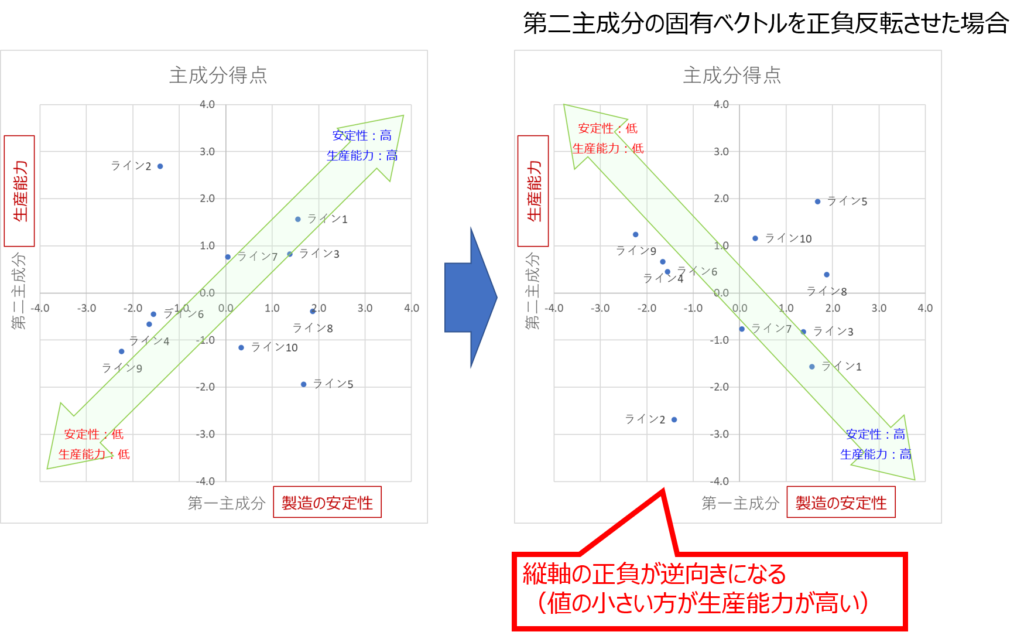
これは単に、「生産能力」の高い・低いを反対に読み替えれば良いだけのことで、後で解析者が意味付けするというのは、二次元マップのネーミングをどのように付けるか次第なのです。
ちなみに、この性質を利用して、見やすいマップを作るテクニックもあります。
例えば、今回の事例のように、第一主成分、第二主成分ともに$v1=-1$を初期値とすると、右下がりのマップが得られます。
何となく直感的に右上がりにしたいな・・と思いますよね。
この場合には、反転させたい主成分の初期値の正負を反転させて、再度ソルバーで計算すれば、意図した軸の向きの結果が得られます(正負反転だけなので手入力で結果を編集してしまっても問題ないです)。
冒頭に説明した通り、主成分分析の目的はデータの傾向分析と情報共有ですので、第三者にも見やすい二次元マップを作ることも心がけてみてはいかがでしょうか。
まとめ
マトリックスデータ解析法の散布図をExcelで作る方法を紹介しました。
平均値や標準偏差のように普段よく使う関数の他、相関係数や行列の関数も登場するので、必要なものを覚えておきましょう。
- 計算に必要な関数
平均値:AVERAGE
標準偏差:STDEV.P(母集団)またはSTDEV.S(標本)
相関係数:CORREL
行列式:MDETERM
行列の積:MMULT
平方根:SQRT
固有値、固有ベクトルの計算方法も覚えておきましょう。
- 固有値
使う機能:ゴールシーク
数式入力セル:det
目標値:0
変化させるセル:$λ$ - 固有ベクトル
使う機能:ソルバー
目的セルの設定:$(A-λE)x$の二乗和
指定値:0
変数セルの変更:固有ベクトル($v1~v5$)
制約条件:固有ベクトルの大きさが1
専用ソフトやマクロ機能を使わないので手順は多くなりますが、Excelの基本機能だけで十分にマトリックスデータ解析法の散布図を作ることができます。
手軽に試せるので、ぜひ活用してみてください。




コメント