「二元配置実験のデータをエクセルで解析したい」
「エクセルのアドイン機能を使って手軽にやりたい」
「自力で関数を使って計算できるようになりたい」
このような悩みをお持ちの方に向けた記事です。
二元配置実験は二つの因子を変化させて特性値への影響を調べるための手法で、反復試行の有無によって種類が分類されます。
このうち繰り返しのない実験では、因子の交互作用を調べられませんが、その一方で実験を簡略化して手間を省けるメリットがあり、特徴を押さえて覚えておきたい手法の一つです。
この記事では、繰り返しのない二元配置実験を対象として、エクセル関数を使ったデータ解析方法、アドイン機能を使った手軽な解析の方法の2種類について詳しく解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
二元配置実験とは?
二元配置実験とは二つの因子を変化させて特性値への影響を調べるための実験手法です。
例えば次の実験のように、製品の加工温度と添加剤の比率を変えてデータを取得するような実験計画のことを指します。
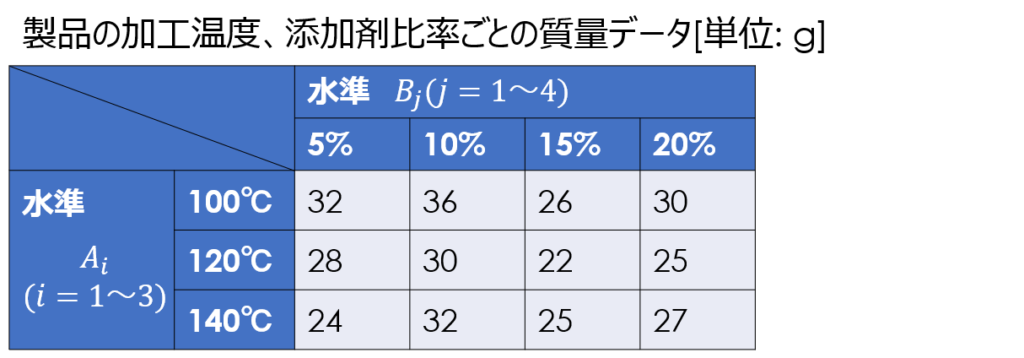
特性値への影響の度合いとしては、分散を用いて水準どうしを比較し、水準間の分散が水準内の分散よりも十分に大きい場合に、水準による効果が大きいと判断します。
分散の比はF検定を用いることで、定量的な基準で判定することができます。
二元配置実験では因子を二つ扱うので、因子単独での特性値への影響「主効果」、因子どうしの条件の組み合わせによる影響「交互作用」を考慮することが必要です。
交互作用とは、二つ以上の因子が組み合わさったときに、ある特定の条件で相乗的、あるいは相殺的に特性値に影響を及ぼす作用のことです。
例えば、添加剤の配合比率と加工温度のような関係が該当します。
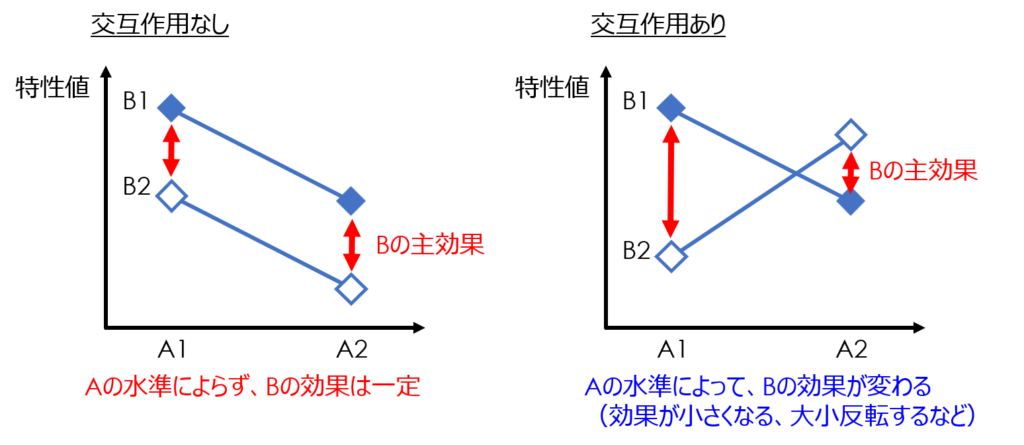

相性みたいなものかな
なお、二元配置実験の基本的な考え方や手順については、以下の記事で詳しく解説していますので、合わせてご覧ください。


アドイン機能を用いたデータ解析の方法
エクセルを使った二元配置実験のデータ解析のやり方としては、アドイン機能を使って手軽に行う方法と、関数を使って自力で解く方法の2つがあります。
まずは、簡単にできるアドイン機能を使った方法から紹介します。
手順
アドイン機能を有効にする
まず、Excelの設定をしましょう。
「ファイル」→「その他」→「オプション」を選択します。
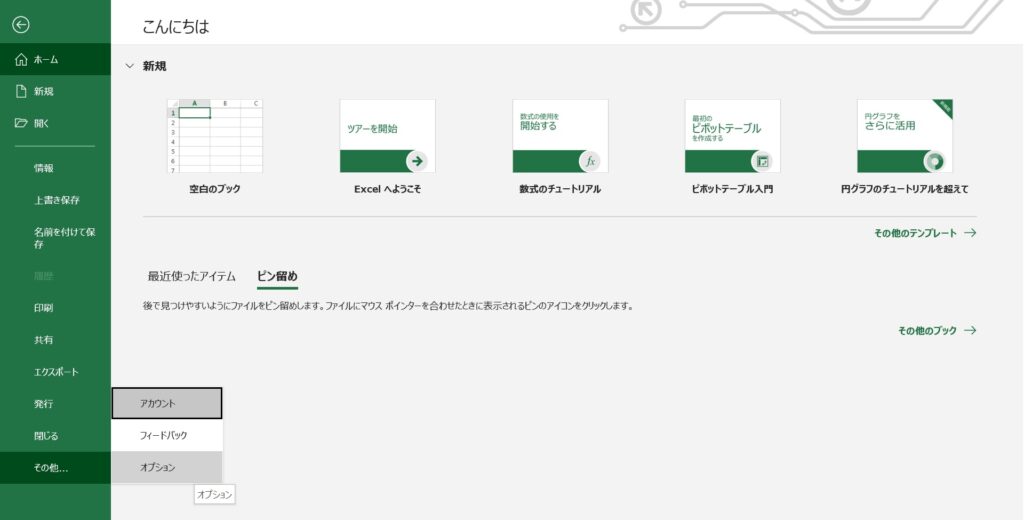
「アドイン」→「設定」を指定し、「分析ツール」にチェックを入れて有効化します。
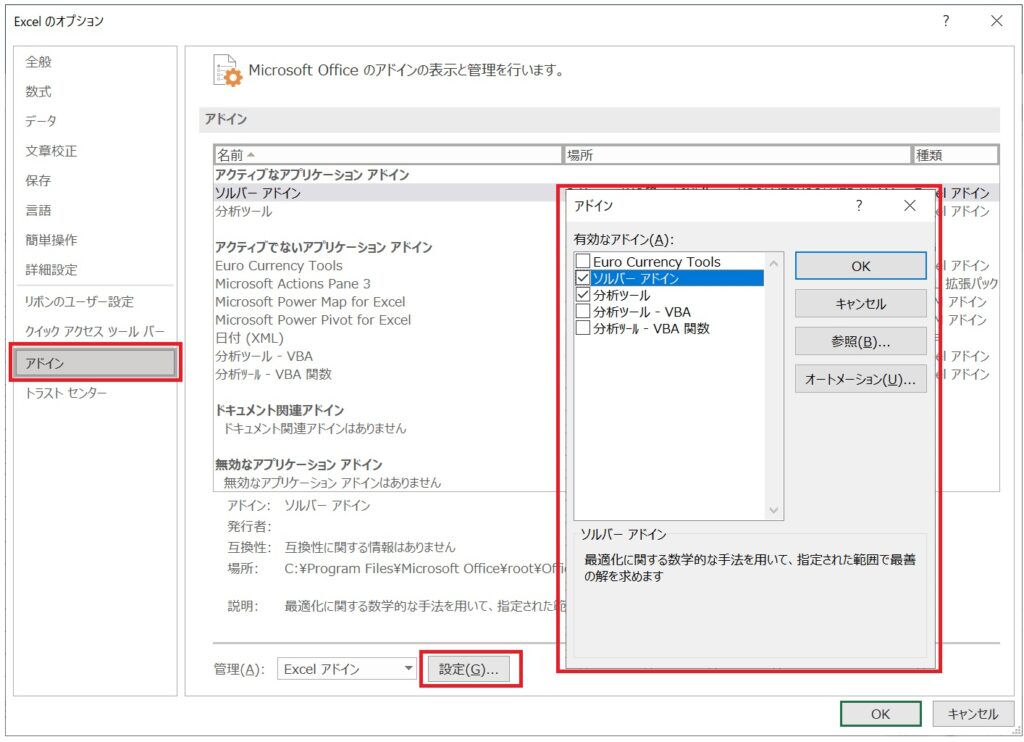
データをマトリックス状に入力する
次に、二元配置実験で得られたデータをマトリックス状に入力します。
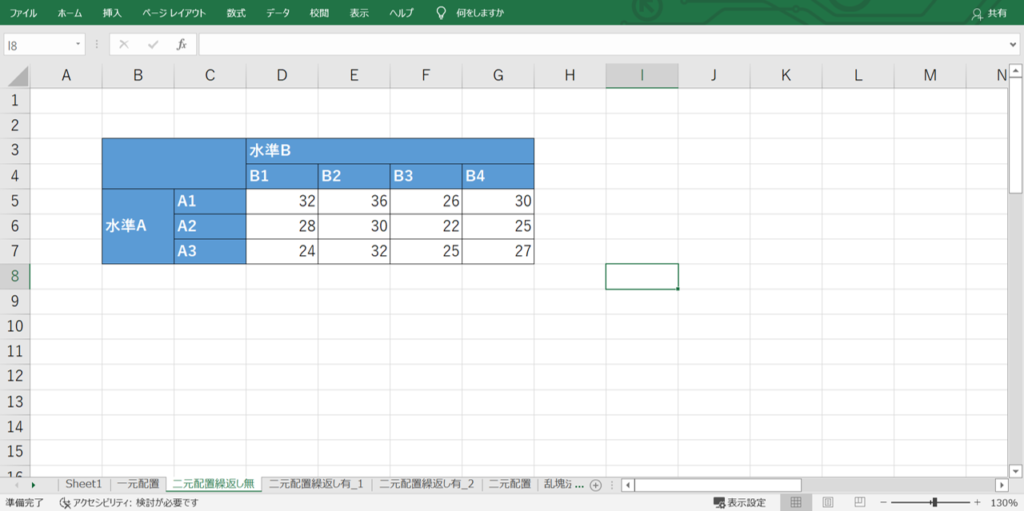
行と列のどちらにどの因子を置いても良いですが、アドイン機能で解析した結果が行⇒列の因子の順で表示されます。
そのため、因子Aと因子Bと名付ける場合には、因子Aを行、因子Bを列に配置した方が正しく並んで表示されるので分かりやすいです。
データ範囲と有意水準を設定する
次に、アドイン機能を用いて二元配置実験のデータ解析を行います。
「データ」タブの「データ分析」をクリックし、「分散分析:繰り返しのない二元配置」を選択します。
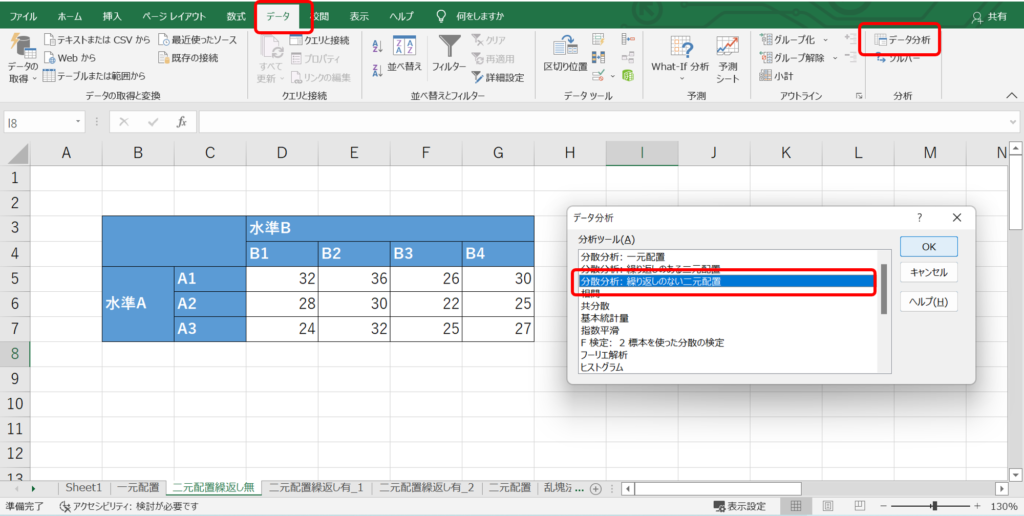
入力範囲に特性値のデータ範囲を設定します。
「ラベル」にチェックを入れない場合は特性値のデータ範囲のみ、チェックを入れる場合には因子のデータラベルの範囲を含めて選択します。
また、F検定の有意水準として$α$を設定します。
デフォルトでは、0.05(5%)が設定されています。
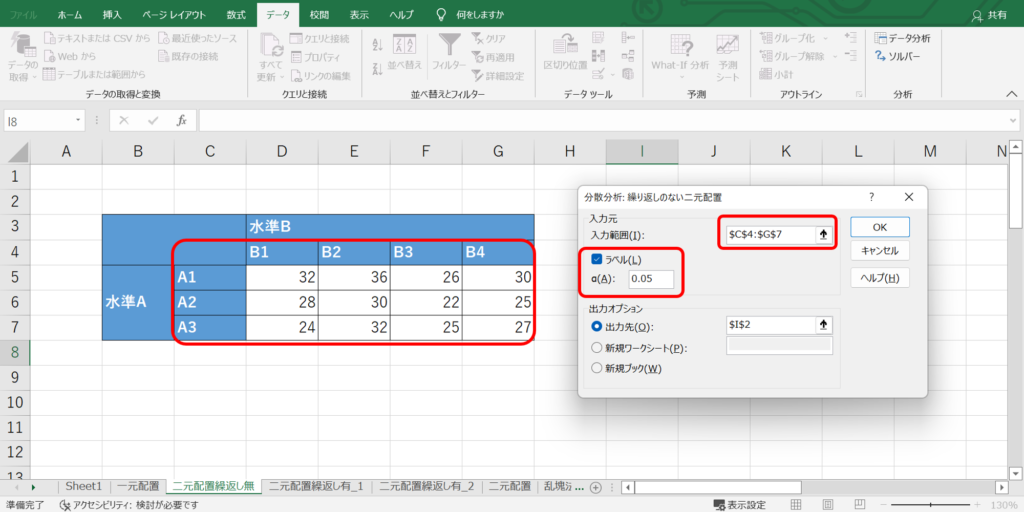
最後に結果の出力先を設定したら、「OK」を押して完了です。
結果の見かた
各項目の意味
それでは、得られた結果が何を意味するのか、見ていきましょう。
まず、「概要」で示す表は見て分かる通り、基本統計量が算出されています。
ここで示す「分散」は、標本データから求めた不偏分散を意味します。
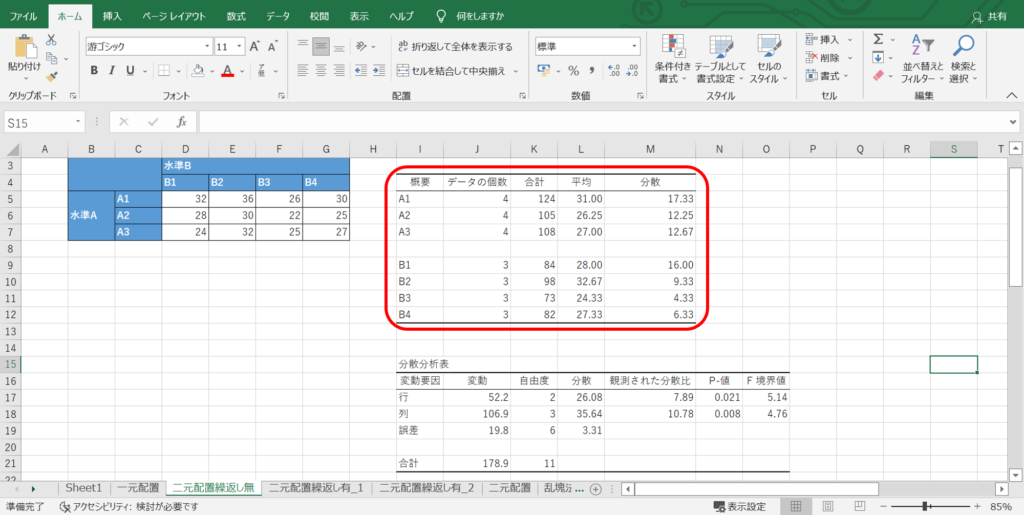
ここまでは、わざわざアドイン機能を使わなくても簡単に求められますね。
次に、本題の「分散分析表」を見てみましょう。
「変動要因」の「行・列」と「誤差」というのは、それぞれ水準間と水準内ということを意味しています。
冒頭にも触れた通り、分散分析は水準間の分散と水準内の分散の比によって有意性を検定するものですので、要因を分割して計算する必要があります。
「合計」というのは水準間変動と水準内変動を合わせたもので、全変動を意味します。
「変動」は偏差平方和(平均値と各データの差分の平方和)のことを表します。
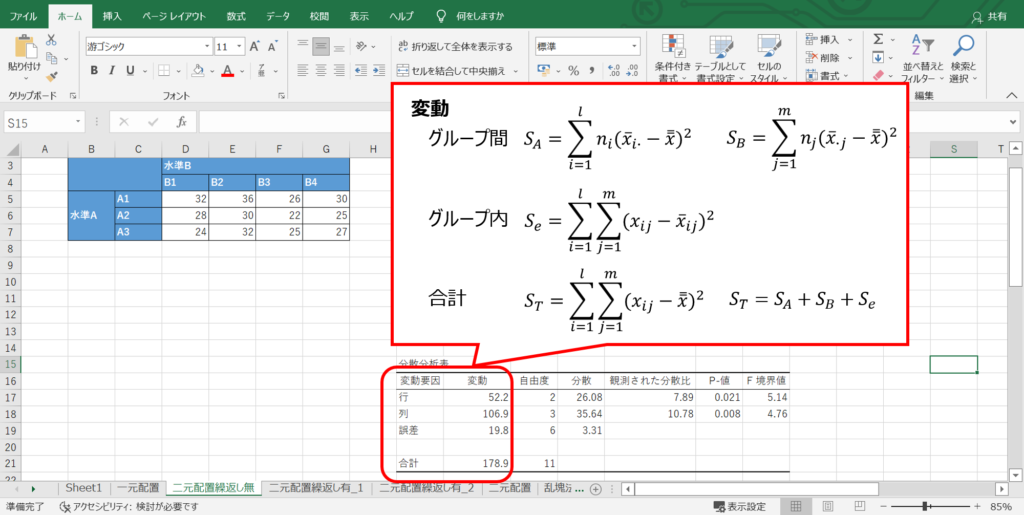
水準間変動、水準内変動、全変動の定義と求め方は次のようになります。
水準間変動$S_{A},S_{B}$:(全体の平均と水準の平均との差)の二乗和
水準内変動$S_{e}$:(各データと水準内平均との差)の二乗和
全変動$S_{T}$:(各データと全体平均との差)の二乗和
全変動$S_{T}$=水準間変動$S_{A}$+水準間変動$S_{B}$+水準内変動$S_{e}$

偏差平方和の考え方は一次元でも二次元でも同じ
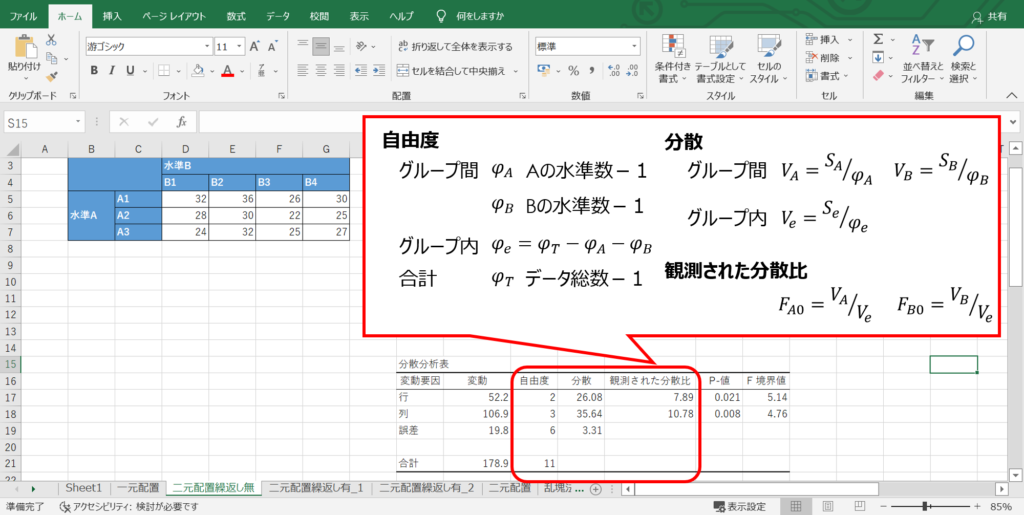
また、自由度、分散、観測された分散比は、次のように求められます。
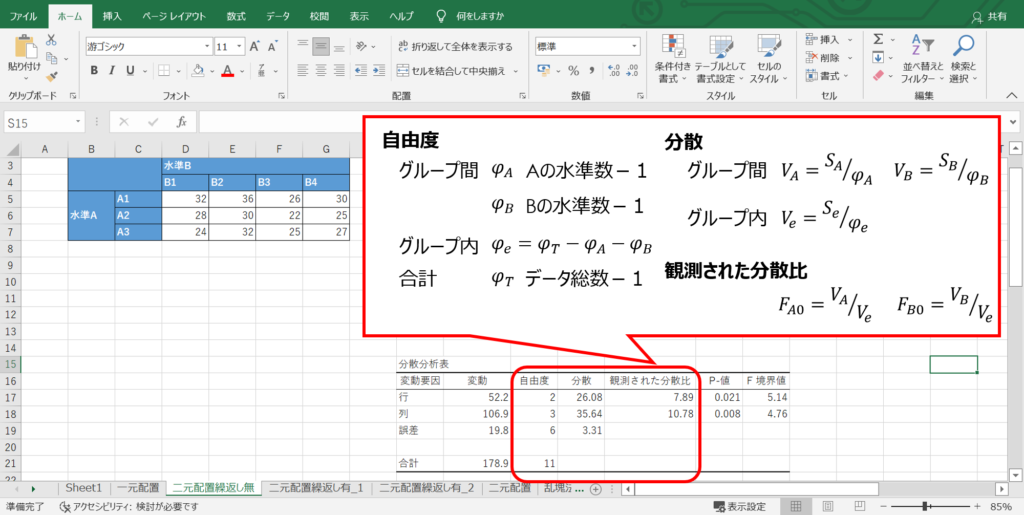
観測された分散比がF検定での検定統計量となります。
結果の判定
アドイン機能では便利なことに、F検定の検定結果まで計算してくれます。
その判定指標となるのが「P-値」と「F境界値」です。
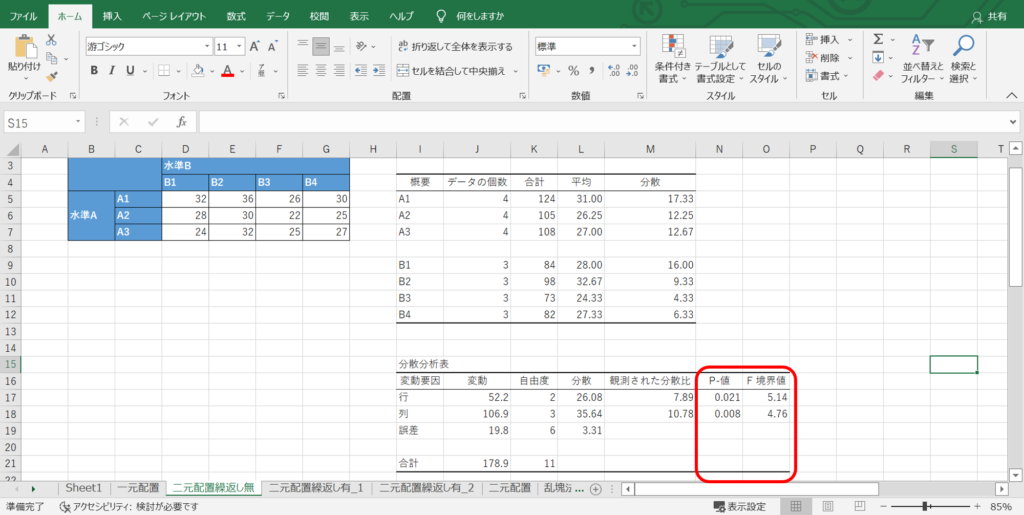
P値は先ほど求めた検定統計量(観測された分散比)に該当する確率のことであり、分散比が大きいほど値が小さくなります。
つまり、今回の場合、水準間変動が大きいとは言えない確率が0.025(=2.5%)しかなく、裏を返すと水準間の影響が十分に大きいと判断できるのです。
判定の基準としては一般的に5%や1%を用いるので、これより値が小さければ、水準の違いがあると考えて良いでしょう。
なお、「F境界値」というのは、最初に設定した有意水準に該当するF値であり、今回の場合は5%に相当する値が出力されています。
分散比がこれよりも大きい値なので、F境界値と分散比の大小関係からも有意性を判断することができます。
エクセル関数を使ったデータ解析の方法
次にエクセル関数を用いて自力で計算をする場合の手順を説明します。
アドイン機能を用いれば簡単に答えを出せますが、その反面どのような計算から導き出されたものか理解しないまま使ってしまう恐れがあるので、応用が利きません。
計算自体は複雑なものではないので、一度は自力で計算してみることをおススメします。
手順
「概要」の表で出力される項目は、いずれも基本的な関数ばかりなので詳細は割愛します。
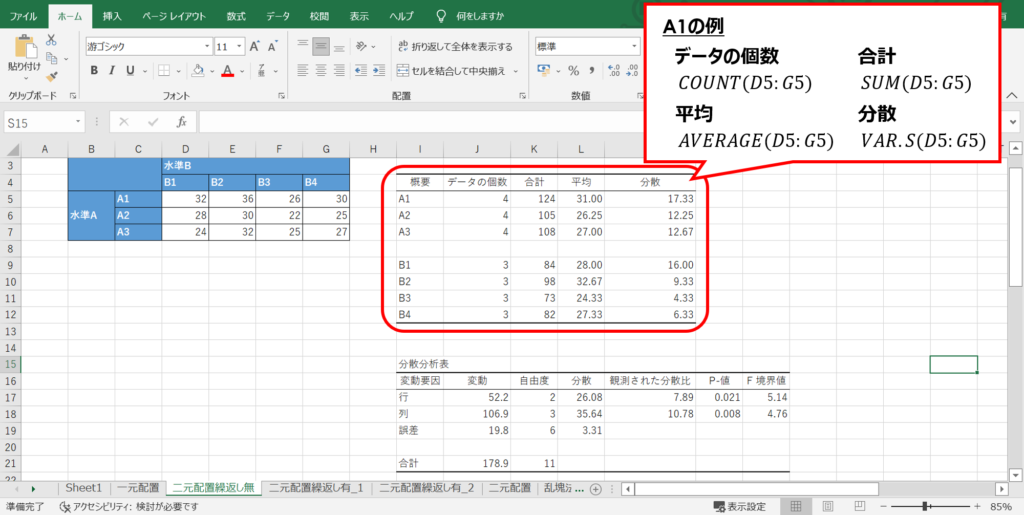
次に「分散分析表」ですが、まずは全変動と水準間変動の偏差平方和を求めるところから始めます。
全変動に関しては便利な関数があり、DEVSQ関数を用いて全データ範囲を指定すれば、偏差平方和を一発で求めることができます。
水準間変動については関数がないので、自力で求めるしかありません。
ここで、先ほど説明した定義の式を一つずつ計算していては大変な労力がかかってしまいます。
そこで、以下の変換式で計算を簡略化します。
CTで示す項は修正項と呼び、特に電卓で計算が必要な場合などは重宝するので、必ず覚えておきましょう。
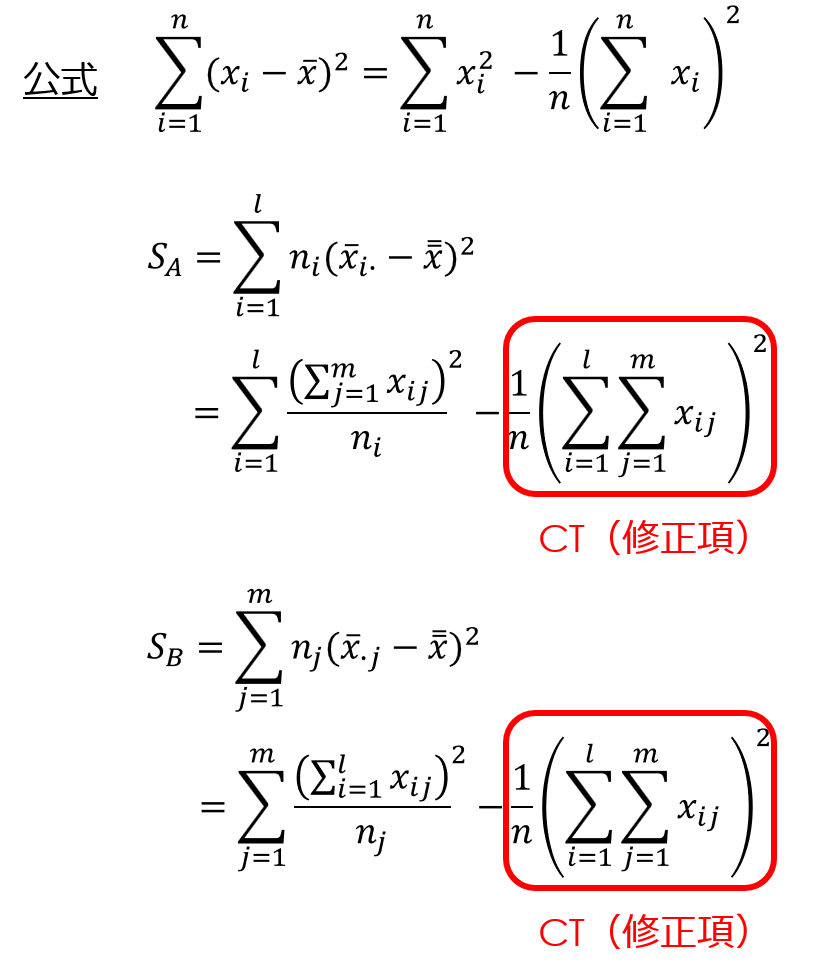
水準内変動については、全変動から水準間変動を引けば求められます。
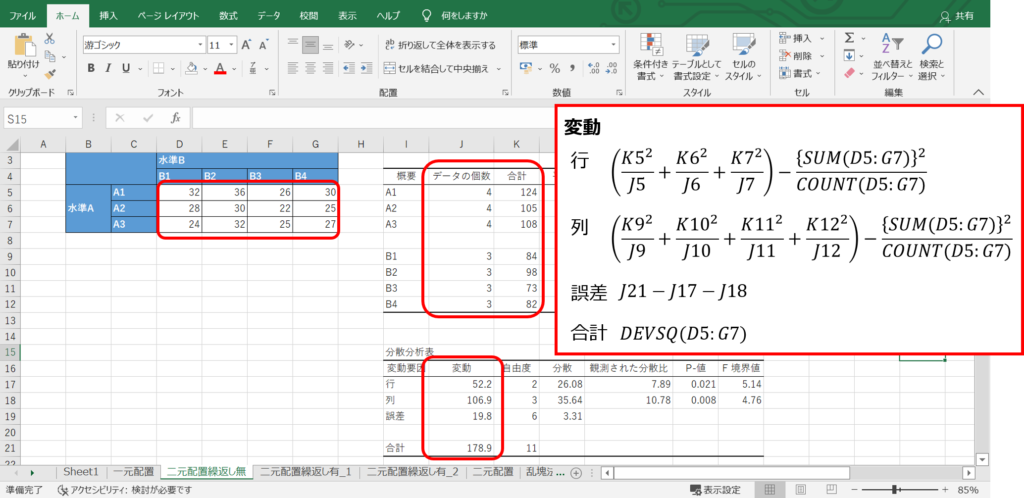
自由度、分散、観測された分散比は、先ほどにも説明した通り関数を使わずに単純な計算で求められます。
次にP-値ですが、これはF分布の上側(右側)確率を返すF.DIST.RT関数を用いれば、あとは分散比と自由度を入れるだけで求められます。
また、F境界値はF分布の上側逆関数を返すF.INV.RT関数を用いれば、有意水準と自由度を入れて求められます。
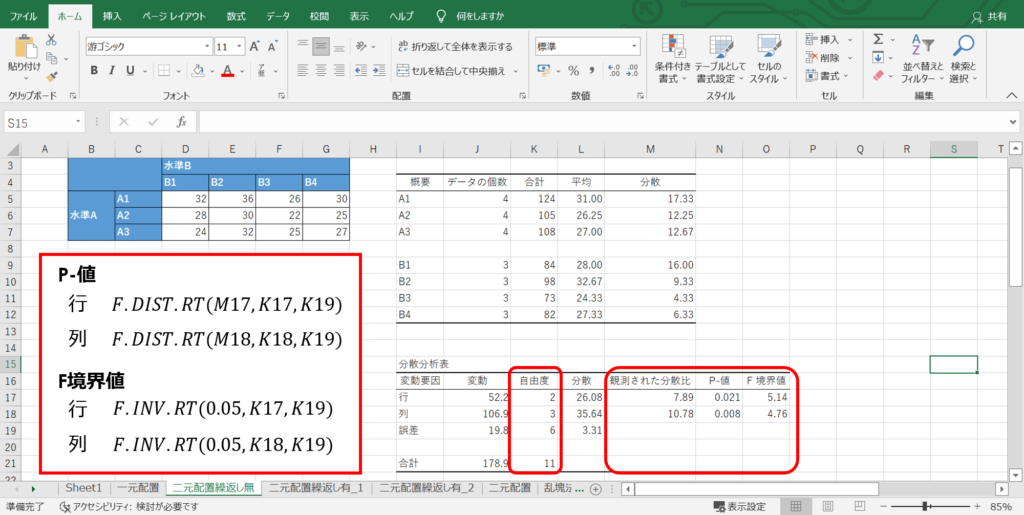
今回の場合、有意水準を0.05としています。
これで、アドイン機能と同じ表を関数計算で作ることができました。
信頼区間の求め方
最後に信頼区間の求め方を紹介しておきます。
実験データから得られた平均値はあくまで標本平均であり、母集団の平均値(母平均)の推定値に過ぎません。
そのため、母集団の平均値には推定の「幅」があり、例えば信頼度95%で○○~△△の範囲に収まるといった表現をします。
二元配置実験では、次の計算式から信頼区間を求めることができます。

水準内変動の自由度と信頼度に対応するt値、水準内変動の不偏分散から計算でき、エクセルの関数を用いて計算すると次のようになります。
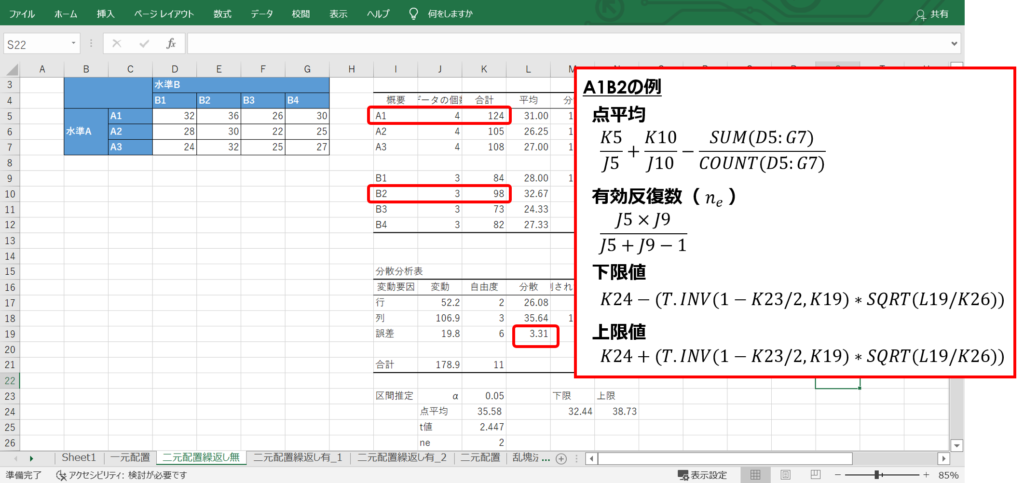
T.INV関数はt分布の逆関数を返す関数で、区間の信頼度と自由度から求められます。
残念ながら、信頼区間はアドイン機能では計算してくれませんので、自力で導出するしかありません。
ただ、計算自体は複雑なものではないので、計算式だけ覚えておけば特に問題ないことと思います。
なお、有効反復数($n_{e}$)については、以下のいずれかの式を用いて算出することができます。
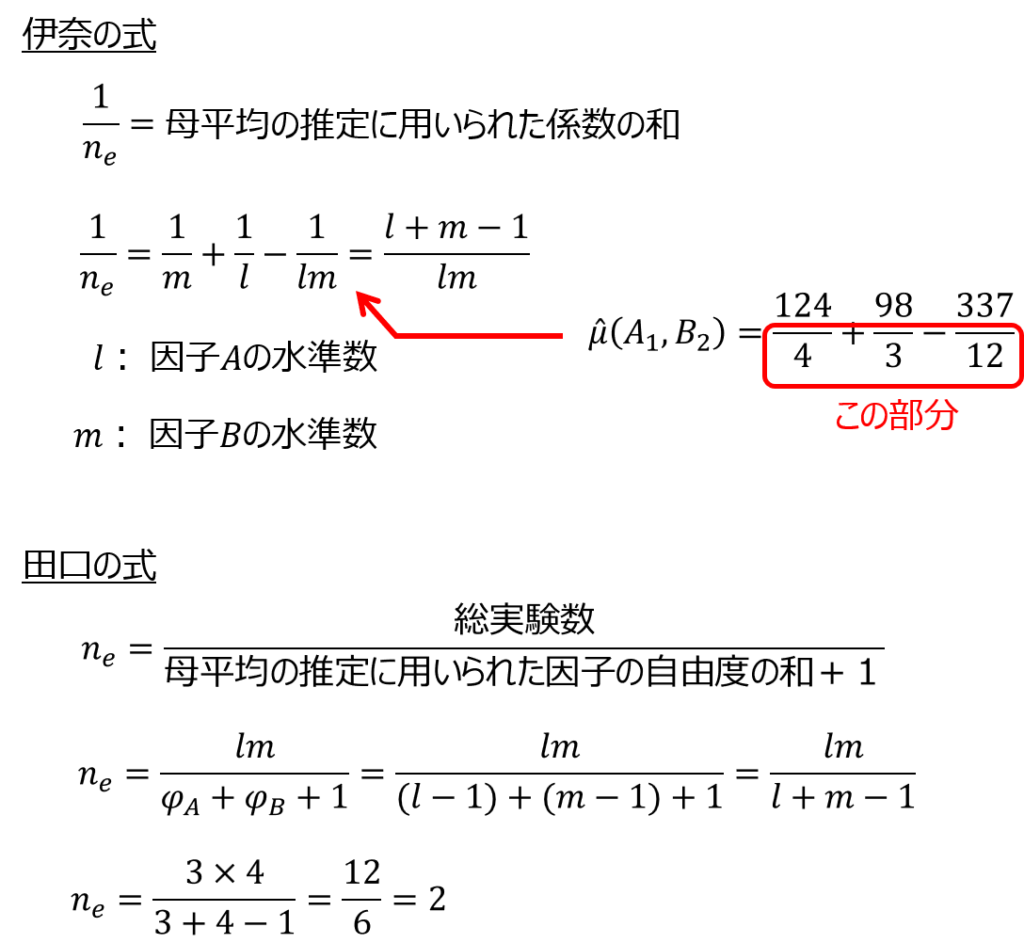

自分で関数を設定できれば標準の様式として使えるね
まとめ
自力で計算するのに使える主なエクセル関数を整理しておきます。
- COUNT関数:データの個数
- SUM関数:総和
- VAR.S関数:不偏分散
- DEVSQ関数:偏差平方和
- F.DIST.RT関数:F分布の上側確率
- F.INV.RT関数:F分布の上側逆関数
- T.INV関数:t分布の逆関数
- SQRT関数:平方根
最後までご覧いただきありがとうございました。
数式の苦手な方でも安心の入門編。
回帰分析、検定、実験計画法まで幅広く、エクセルを用いた実践方法も習得したい方に。
乱塊法、分割法もお任せ! QC検定1級の教材としてもおススメ。




コメント