「二元配置実験って一元配置とどう違うの?」
「繰り返しのありなしって何が違うの?」
「分散分析と信頼区間の求め方を知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
二元配置実験は二つの因子を変化させて特性値への影響を調べるための手法で、一元配置実験の次元を拡張したものです。
ただ、単に因子が二つになって実験の組み合わせ数が増えるだけではなく、因子どうしの相互作用を考慮しながら因子の効果の有無を見極めなければなりません。
また、二元配置実験では実験の繰り返しがある場合とない場合に分類され、因子の影響を調べられる範囲が異なります。
この記事では、繰り返しのない二元配置実験を対象として、一連の流れ、一元配置実験との違い、分散分析と信頼区間の計算手順について解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
また、Youtubeチャンネルでも繰り返しのない二元配置実験の手順を解説していますので、あわせてご覧いただけると幸いです。
二元配置実験とは?
二元配置実験とは二つの因子を変化させて特性値への影響を調べるための実験手法です。
因子というのは、条件の変化によって特性値に影響を与えると考えられるもののことを意味し、例えば製品を加工する際の温度や圧力といった要因が該当します。
また、水準とは実験にあたって因子を変動させる場合に代表値として選んだ値のことで、例えば、100℃、120℃、140℃といったように自らが設定する条件を意味します。
次のような条件と結果の対応表が一例として挙げられます。
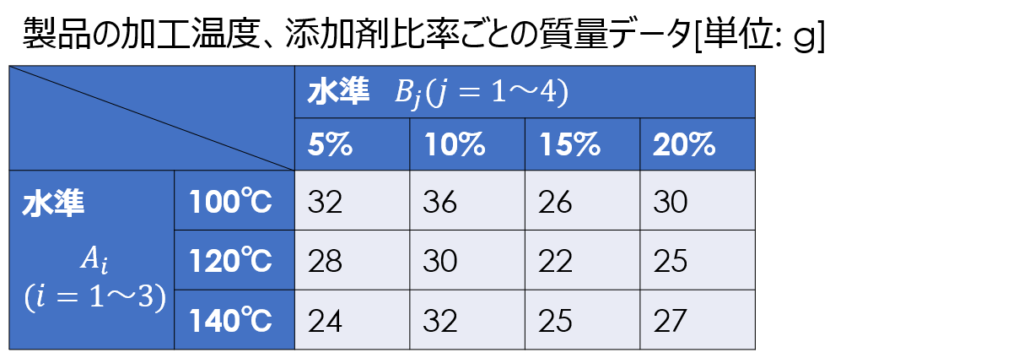
二つの因子を行と列に配置し、水準の数を掛け合わせて通り数を決めるもので、総当たり実験として感覚的にも理解しやすいのではないかと思います。
ここで、二元配置実験は実験の繰り返しがあるかないかで、二つのケースに分類されます。

フィッシャーの3原則によると実験の精度を高めるには反復試行が望ましいですが、時間とお金の都合から現実的に難しいこともあります。
このような場合に、二元配置実験では繰り返し試行を行わなくても、因子の主効果を調べることができるのです。

じゃあ、実験の量を減らせて単純に楽ちんなのかな
ただし、実験の手間を省けるだけの都合の良いものではありません。
繰り返しを行わないデメリットとして、因子どうしの相互的な影響(交互作用)を調べられないのです。
ただ、因子どうしの関連性が全くないことが自明な場合であれば有効に使える手段なので、特徴を踏まえて適切な手法を選びましょう。
なお、実験計画法の考え方やフィッシャーの3原則など基本から確認し直したい方、一元配置実験から学び直したい方は、以下の記事も合わせてご覧ください。

交互作用とは?
さて、二元配置実験の特徴が分かったところで、先ほど登場した「交互作用」について説明しておきます。
交互作用とは、二つ以上の因子が組み合わさったときに、ある特定の条件で相乗的、あるいは相殺的に特性値に影響を及ぼす作用のことです。
例えば、添加剤の配合比率と加工温度のような関係が該当します。
添加剤の比率を段階的に変えた場合に、ある温度では全く効果が見られなかったとしても、別の温度では効果が現れ、特定の条件で特に大きな効果を示す場合があります。
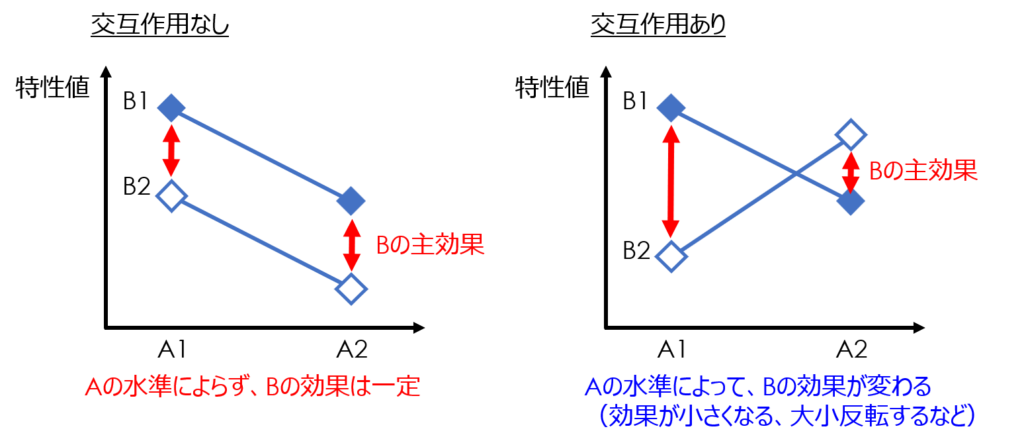
因子が単独で作用する影響のことを「主効果」と呼び、これと対比する形で相互的な影響のことを「交互作用」と呼ぶのです。
それでは、繰り返しのない二元配置実験では交互作用の影響を調べられないのは、どうしてでしょうか?
それは、得られた実験結果が偶然によるものか必然なのか切り分けができないからです。
各条件につき、一回しかデータを取得しない場合ですと、その条件内でのばらつきの程度を比較することができません。
そのため、交互作用の有無を明確にしたい場合には繰り返しを行って、組み合わせ効果による変動の大小を解析する必要があるのです。
このように、一元配置実験では一つの因子の影響だけ考慮すれば良かったのですが、二元配置実験では交互作用の考え方が登場するので、違いを把握しておきましょう。
繰り返しのない二元配置実験の手順
実験計画法の考え方
二元配置実験に限らず、実験計画法では分散分析の考え方を用いて水準間の有意差を調べます。
分散とは「データのばらつき」のことで、水準間の分散と水準内の分散の比を求めて、水準間の分散が十分に大きければ、水準の違いによる効果が大きいと判定します。
なぜ、分散を見る必要があるかというと、水準が3つ以上になる場合、データどうしを単純に比較できないからです。
例えば、水準が2つしかない場合、データどうしの差を取ってt検定を行えば、差がないと言えるか否か判断することができます。

しかし、水準が3つ以上になると、データの差をとる組み合わせ通り数が1通りでなくなるので、同じやり方を用いるわけにはいきません。
そこで、各水準において繰り返しデータを取得してばらつきを求め、これを指標にするという考え方が実験計画法では用いられるのです。
一連の流れ
二元配置実験の解析手順を次に示します。
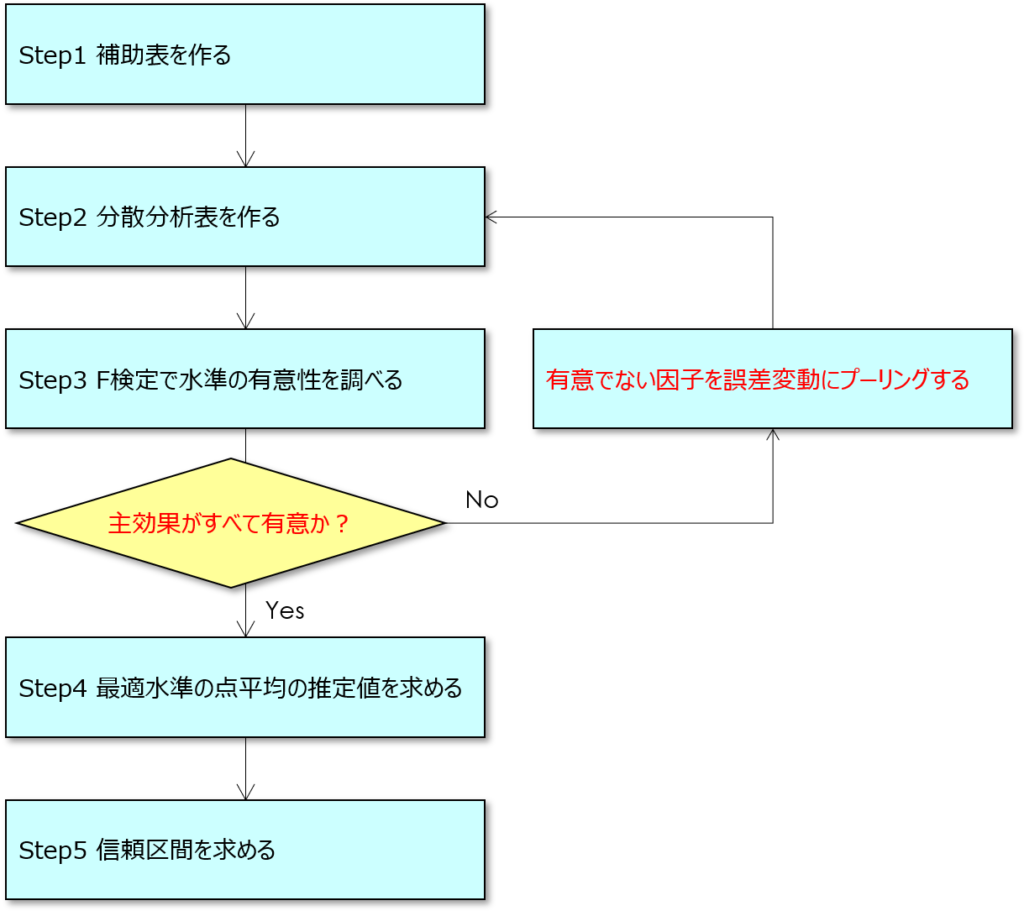
黒い文字で示すのは一元配置実験と同じ項目で、赤い文字で示すのが二元配置実験で新たに登場する手順です。
すでに一元配置実験で流れを習得済みの方は、「誤差変動にプーリングする」までスキップください。
補助表を作る
分散を求めるには、水準ごとの偏差平方和(平均値と各データの差分の平方和)を求める必要があります。
エクセルを用いれば偏差平方和も一瞬で計算できますが、電卓を用いた手計算で行う場合、これが結構大変な労力のかかる作業になるのです。
そこで、次の公式を用いることで偏差平方和を効率的に計算することができます。
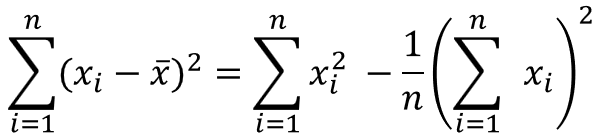
これは、品質管理検定(QC検定)を受検の方には暗記必須の公式で、知っているのと知らないのとでは計算時間に雲泥の差が生じます。
この式の形から分かるとおり、各データの総和、各データの二乗の和を求めれば、あとは簡単な四則演算で偏差平方和を求めることができます。
そのため、補助表として事前に各データの和と二乗和を準備しておくことで、後の計算が非常に楽になります。
分散分析表を作る
次に水準間変動(群間変動、級間変動とも呼びます)と水準内変動についての分散分析表を作成します。
まず、全変動とは「各データと全体平均との差」を表し、次の式で定義されます。

続いて、水準間変動とは「全体の平均と水準の平均との差」のことを表し、次の式で定義されます。
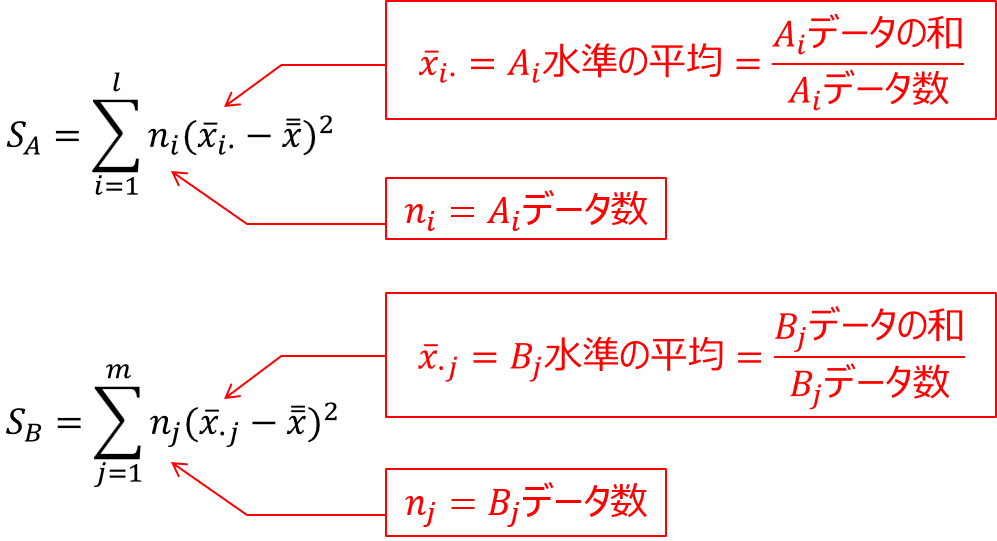
平均の差を二乗しているのは、プラス側とマイナス側の差がキャンセルされるのを防ぐためで、$n_{i},n_{j}$はデータの個数分を合算するための項目です。
最後に水準内変動とは「各データと水準内平均との差」を表し、次の式で定義されます。
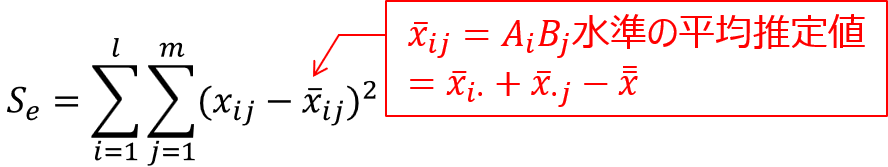
全変動、水準間変動、水準内変動の間には以下の関係式が成り立ちます。
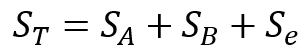
また、分散分析表とは以下のような表で、最終的に分散の比の検定(F検定)を行うための検定統計量を求めるための表です。
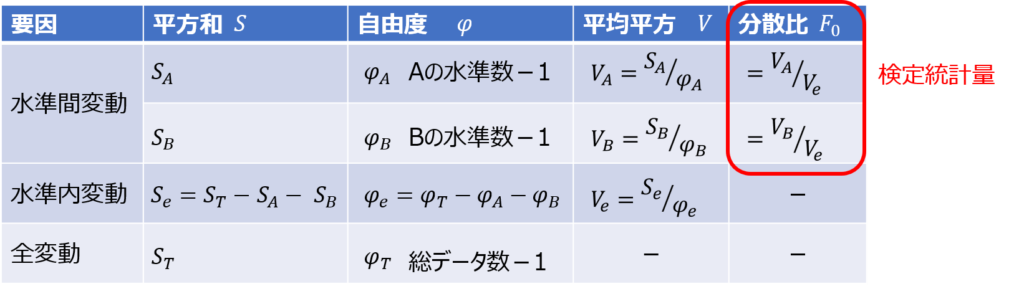
F検定で水準の有意性を調べる
分散分析表からF検定の検定統計量を求められたら、F分布表から有意性を判定します。
検定統計量がある有意水準のしきい値よりも大きい場合、水準間変動が十分に大きいと判定され、その大小関係を比較するだけなので、特に難しく考える必要はありません。


誤差変動にプーリングする
F検定の結果、有意でない因子が見られた場合には、特性値に有意な影響を及ぼさないものと判断し、誤差成分に含めて扱います。
具体的には、有意でない因子の偏差平方和を誤差成分の偏差平方和に加えることを意味し、これを「プーリング」と呼びます。
有意性の判定にはF分布の棄却判定値を用いますが、本当は効果があるのに誤って誤差成分に含めてしまわないよう、一般的には検定統計量が2以下の場合をプーリングします。

プーリングして消去するのは慎重にしよう
最適水準の点平均の推定値を求める
水準の代表値として平均値を求めます。
二元配置実験では最適水準を求める場合が多く、特性値が最大(または最小)となる組み合わせの点平均の推定値を求めます。
信頼区間を求める
最後に各水準の点平均を中心とした信頼区間の幅を求めます。
先ほど計算した点平均は取得したデータから求めた標本平均であり、母集団の平均値(母平均)の推定値に過ぎません。
そのため、母集団の平均値には推定の「幅」があり、例えば信頼度95%で○○~△△の範囲に収まるといった表現をします。
これは95%の確率で○○~△△の範囲に母平均が存在することを意味しています。
標本平均から母平均の幅を推定(区間推定と呼びます)するには、以下の計算式から求めることができます。

自由度と信頼度に対応するt値、サンプルサイズ、不偏分散から信頼区間の幅を求められます。
後ほど詳しく説明しますが、二元配置実験でも同じ形の式から信頼区間を求めることができます。

$μ$の上についている「^」は「ハット」と呼び、推定値を表すときに用いられる記号です。
なお、母平均の区間推定については以下の記事で詳しく解説していますので、合わせてご覧ください。

分散分析のやり方
それでは、具体例を用いて実際に分散分析表を作って、F検定までやってみましょう。
問題
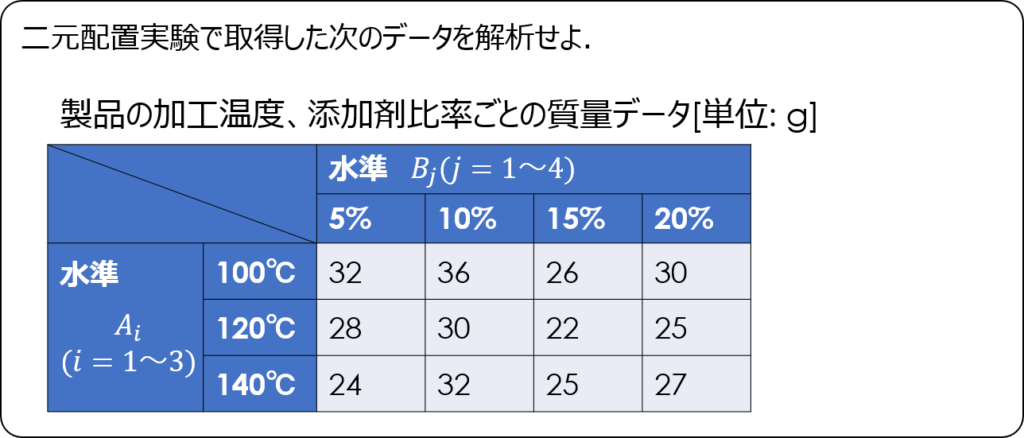
解法の手順
水準ごとの二乗の和を求める
先ほど説明した通り、偏差平方和を求める前に補助表を作成します。
これには水準ごとの二乗の和を求める必要があるので、あらかじめ計算しておきます。
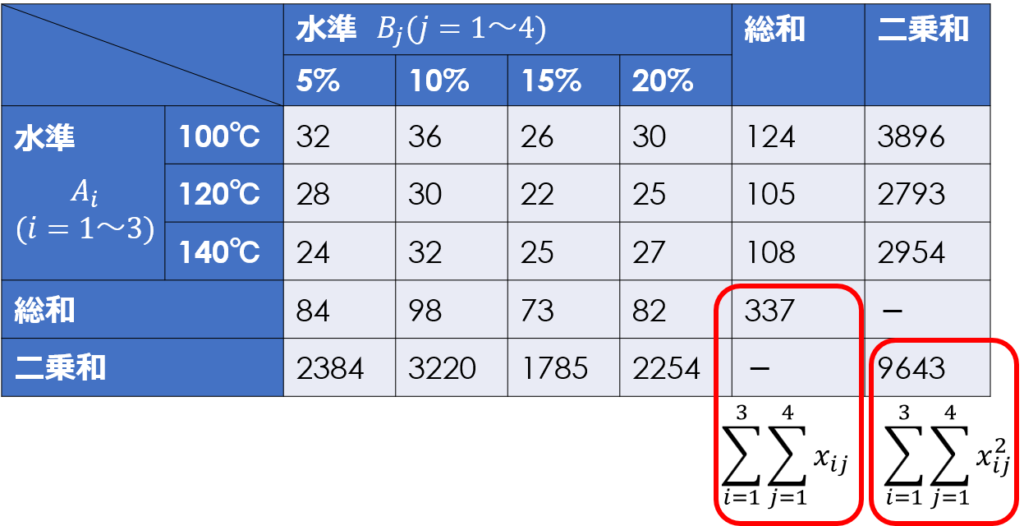
偏差平方和、自由度、分散(平均平方)、分散比を求める
補助表の値を使って、分散分析表を埋めていきます。
全変動の偏差平方和$S_{T}$は次の式で求められます。
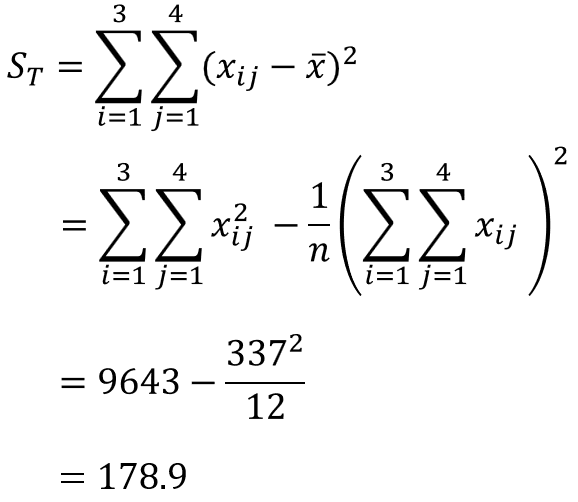
また、水準間変動の偏差平方和$S_{A},S_{B}$は定義の式を変換して、次の式で求められます。

変換の導出は少し複雑なので省略しますが、CTで表す成分を修正項と呼びます。
水準ごとの二乗和の平均値の総和から修正項を引くことで水準間変動の偏差平方和を求められる便利なもので、計算を大幅に簡略化できるため、ぜひ覚えておきましょう。
ここまで、偏差平方和の求め方が少し複雑でしたが、あとは、簡単な四則演算で表が埋められます。
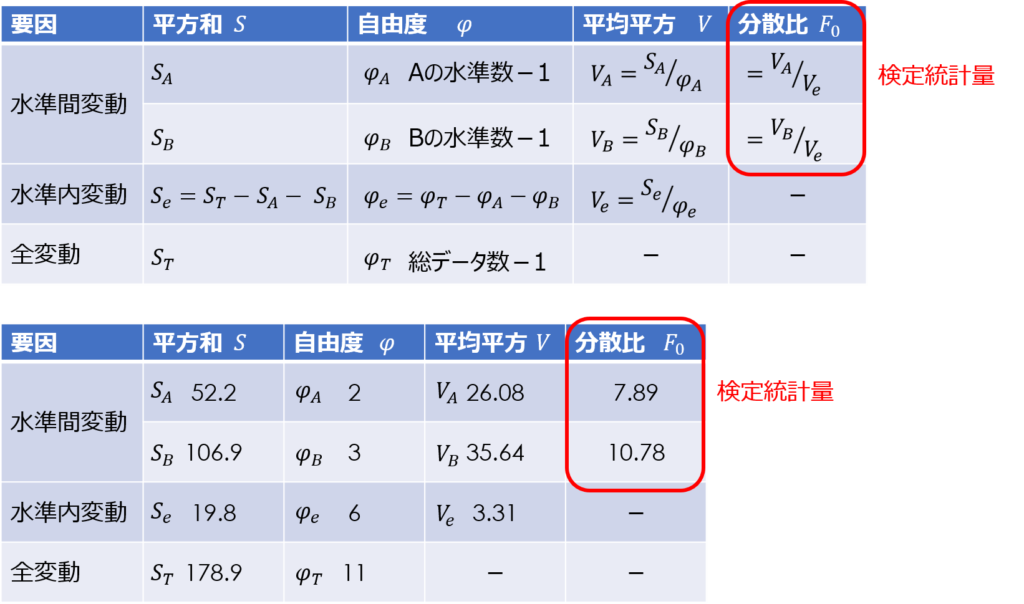
F検定により有意性を判定する
分散比$F_{0}$を検定統計量として、F検定を行います。
判定基準となるF値は、自由度と有意水準が分かればF分布表から対応する値を読み取れば求められます。
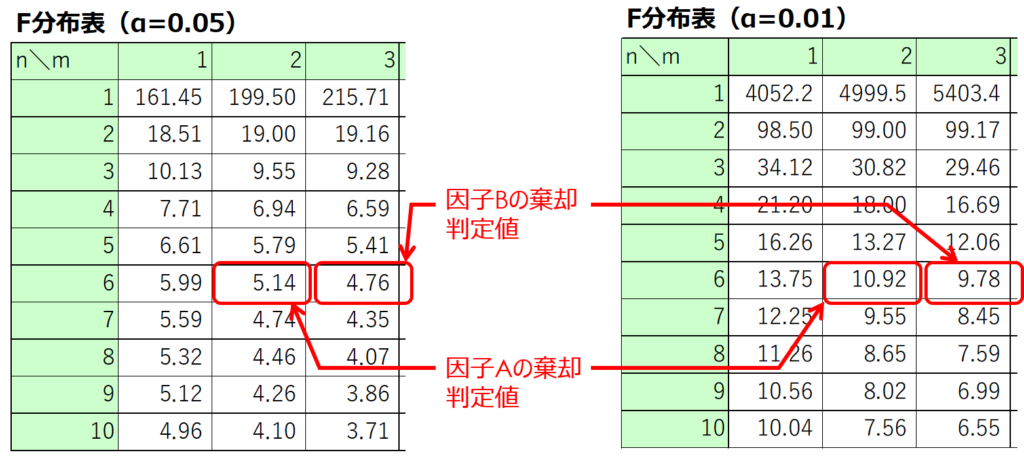
今回の場合、因子Aは有意水準5%、因子Bは有意水準1%で水準間変動に意味があるという結果が得られました。

誤差変動にプーリングする
今回は因子Aと因子Bともに有意であったため、プーリングは行いません。
仮にF検定により、いずれかの因子が有意でない、かつ$F_{0}$の値が2以下という結果が得られた場合には、特性に寄与しないものと判断し、誤差成分として一つにまとめてしまいます。
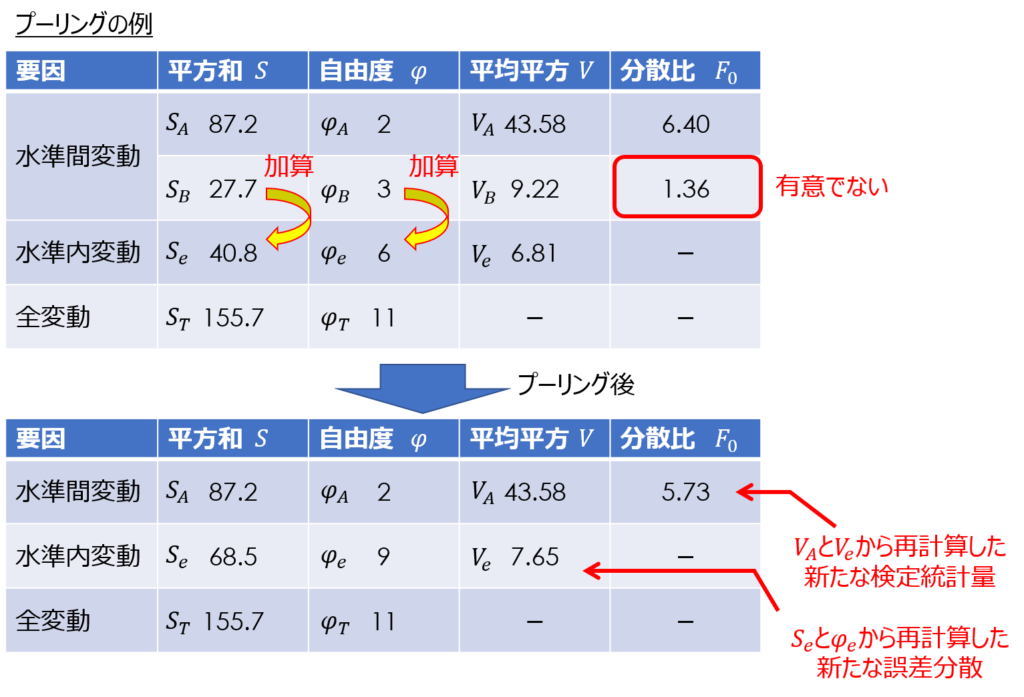
この時、分散比とF検定の棄却判定値が変わるので、プーリング後の分散分析表から再度$F_{0}$の値を検定し直します。
ここでお気づきの方もおられると思いますが、プーリング後の分散分析表は因子Aのみの一元配置実験の分散分析表と同じになります。
それもそのはず、因子Bの影響を無視できるのであれば、因子Bの実験は単に繰り返し試行を行ったものと同義であり、一元配置実験と同じことを意味しているのです。
最適水準の点平均の推定値を求める
先ほどの例に戻って、因子の有意性の判定が終わったら、次に最適水準の点平均の推定値を求めます。
今回の場合、特性値が大きいほど良いとして、質量が最大となる水準の推定値を求めます。
因子どうしの交互作用がない場合、まずは因子Aと因子Bのそれぞれに対して、特性値が最大となる水準を決定します。
今回の場合、因子Aは水準1(100℃)、因子Bは水準2(10%)が最も特性値が大きくなっています。
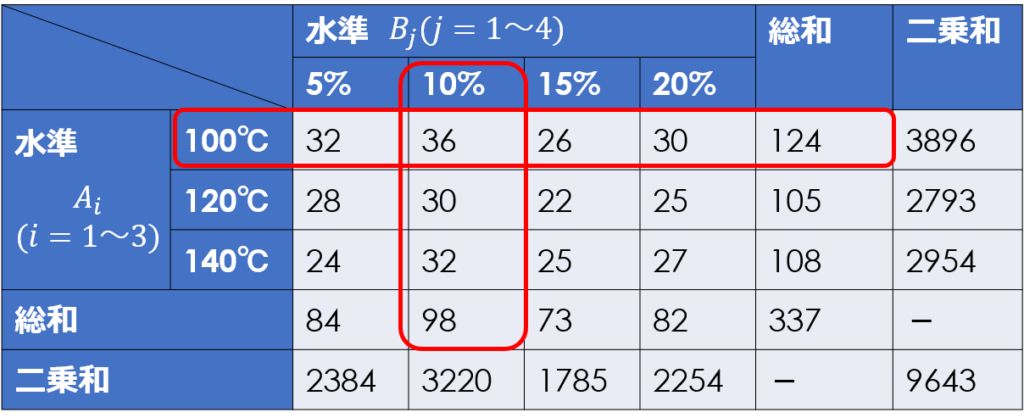
そして、各因子の最適水準を決定したら、以下の式により$x_{12}$の点平均の推定値を計算することができます。
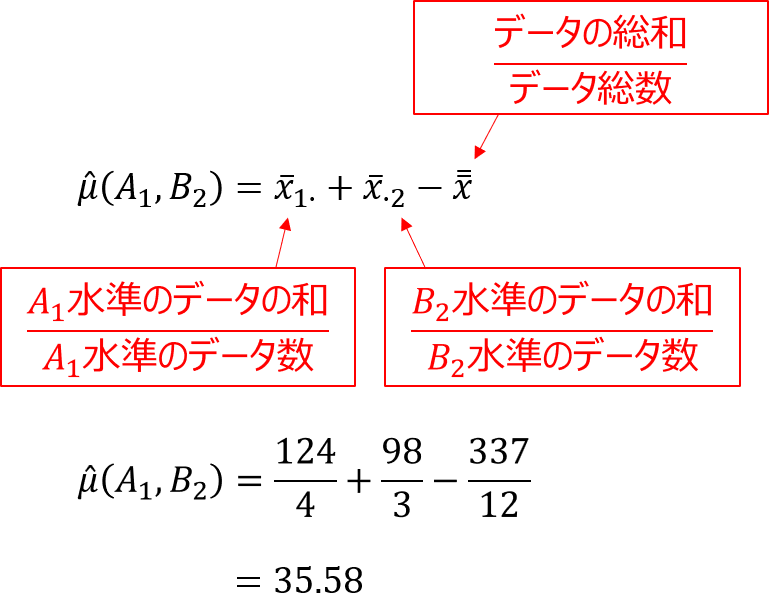
因子Aと因子Bの平均値の平均値を取ったような感じで、最後に全平均を引いているのは、AとBの平均値を加算して2倍値になったのを補正しているようなイメージです。
なお、最適水準に限らず、水準の対象を変えれば同じ計算手順で任意の点平均を求めることができます。
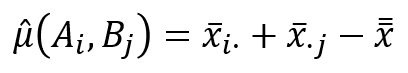
ただし、二元配置実験の場合、組み合わせ通り数が多いので、最適水準以外の推定値を計算することにあまり実用性がなく、必要となるケースは比較的少ないと思います。

一元配置と比べて因子が二つになると考えることいっぱい・・
信頼区間の計算のしかた
信頼区間は先ほどにも少し登場しましたが、以下の式で求めることができます。

実験計画法に限らず、統計的推定でも基本的にはこの形の式しか登場しませんので、何度も復習して覚えてしまいましょう。
ただし、一元配置実験と異なり、因子が二つ以上となる場合には、繰り返し数の定義が少し複雑になります。
単純に実験の繰り返し回数を用いるのではなく、次の式で示す有効反復数($n_{e}$)を用います。
計算式には、伊奈の式と田口の式の二種類がありますが、結局のところ同じ形にたどり着きますので、どちらを用いても構いません。
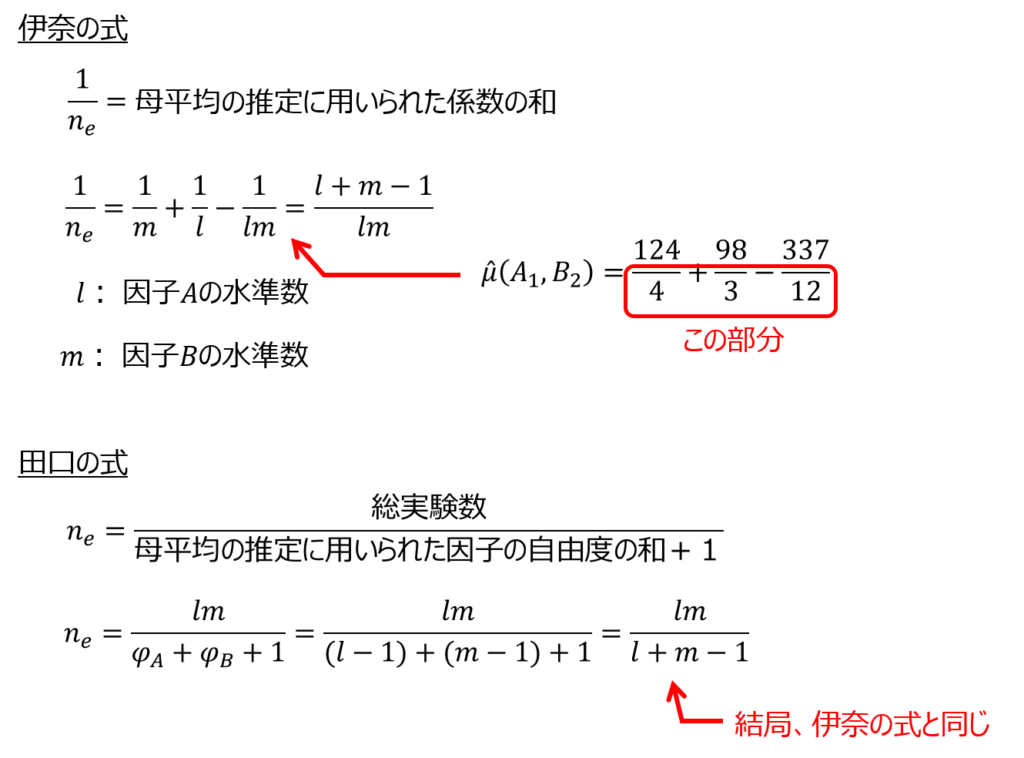
今回の場合、有効反復数は次のように求められます。
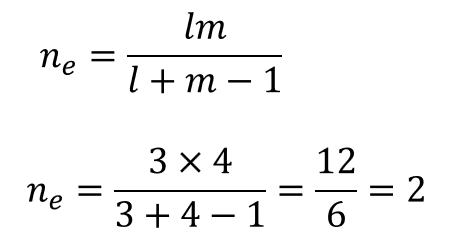
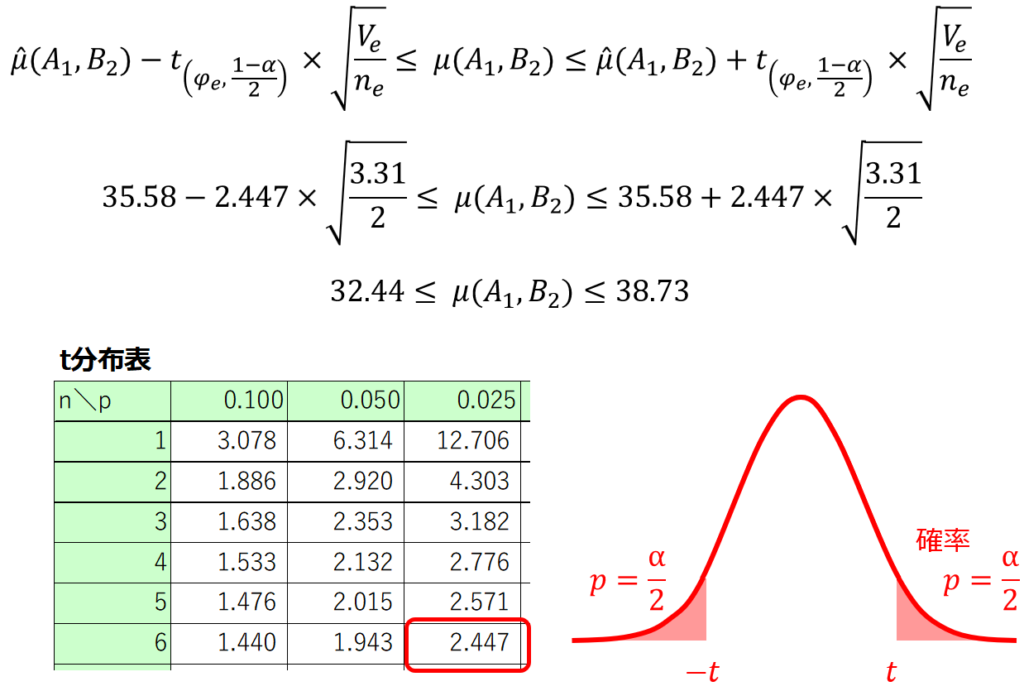
あとは、自由度と有意水準に対応するt値をt分布表もしくはエクセル関数などを用いて求めれば、信頼区間を算出することができます。
まとめ
- 二元配置実験とは
二つの因子を変化させて特性値への影響を調べるための手法 - 交互作用とは
二つ以上の因子が組み合わさったときに、ある特定の条件で相乗的、あるいは相殺的に特性値に影響を及ぼす作用 - 繰り返しのない二元配置実験の流れ
①:補助表を作る
②:分散分析表を作る
③:F検定で水準の有意性を調べる
④:誤差変動にプーリングする
⑤:最適水準の点平均の推定値を求める
⑥:信頼区間を求める
最後までご覧いただきありがとうございました。
数式の苦手な方でも安心の入門編。
回帰分析、検定、実験計画法まで幅広く、エクセルを用いた実践方法も習得したい方に。
乱塊法、分割法もお任せ! QC検定1級の教材としてもおススメ。




コメント