「繰り返しのありなしって何が違うの?」
「交互作用のある分散分析のやり方を詳しく知りたい」
「最適水準と信頼区間の求め方を知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
二元配置実験は二つの因子を変化させて特性値への影響を調べるための手法で、反復試行の有無によって種類が分類されます。
この記事では、繰り返しのある二元配置実験を対象として、一連の流れ、繰り返しのない実験との違い、分散分析と信頼区間の計算手順について解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
また、Youtubeチャンネルでも繰り返しのある二元配置実験の手順を解説していますので、あわせてご覧いただけると幸いです。
繰り返しのある二元配置実験とは?
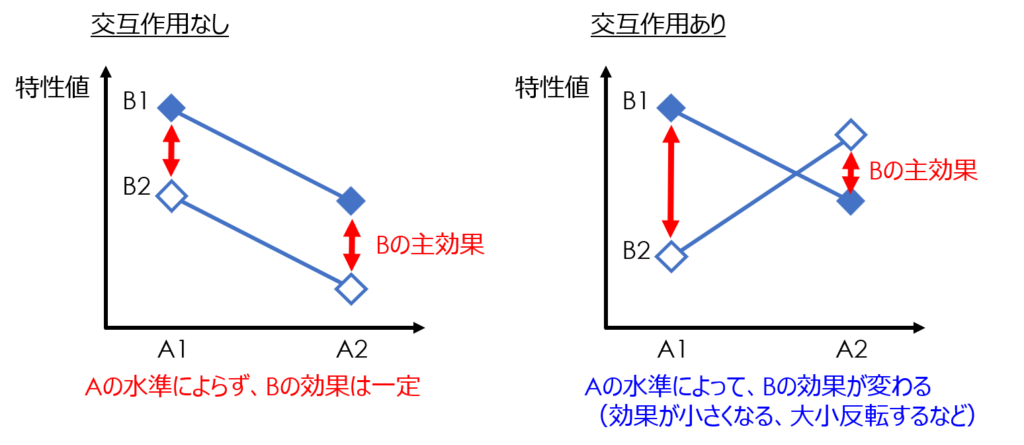
この記事では、繰り返しのない実験とある実験の違いを中心に解説しています。
違いを一言で言うと、「交互作用の影響を調べられるか否か」であり、交互作用まで含めて解析できる「繰り返しのある実験」の方が必要な知識量としては多くなります。
そのため、二元配置実験を一から習得したい方は、まず繰り返しのない実験の解法について学習することをおススメしています。
交互作用の概念、二元配置実験の手順、実験計画法の基本的な考え方については、以下の記事で詳しく解説していますので、ぜひご覧ください。


さて、あらためて繰り返しの有無による違いを整理すると次のようになります。
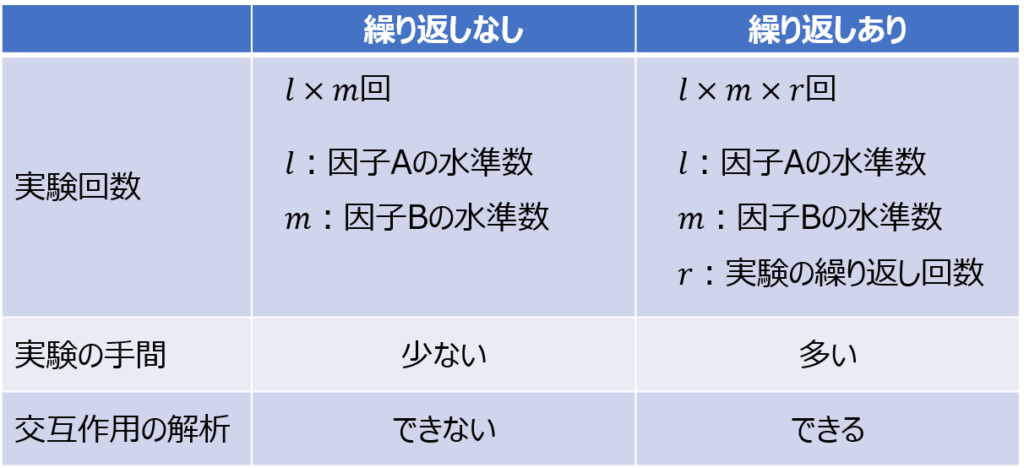
繰り返しのない実験では各水準のデータを1回ずつ取得するのみで、実験を簡略化して手間を省けるメリットがあります。
その一方で、交互作用の影響を解析できず、あらかじめ因子どうしの交互作用のないことが自明な場合や、交互作用を解析する必要のない場合にしか適用できません。
このような特徴に当てはまるケースでは時間やお金の都合を踏まえて簡略化を検討すべきですが、交互作用があるか否かを調べること自体が目的の実験も多くあります。
そのため、基本的にはフィッシャーの3原則における反復試行の考え方にもとづいて、繰り返しデータを取得して因子どうしの交互作用を解析できる方が望ましいです。
繰り返しのある二元配置実験の手順
一連の流れ
二元配置実験の解析手順を次に示します。
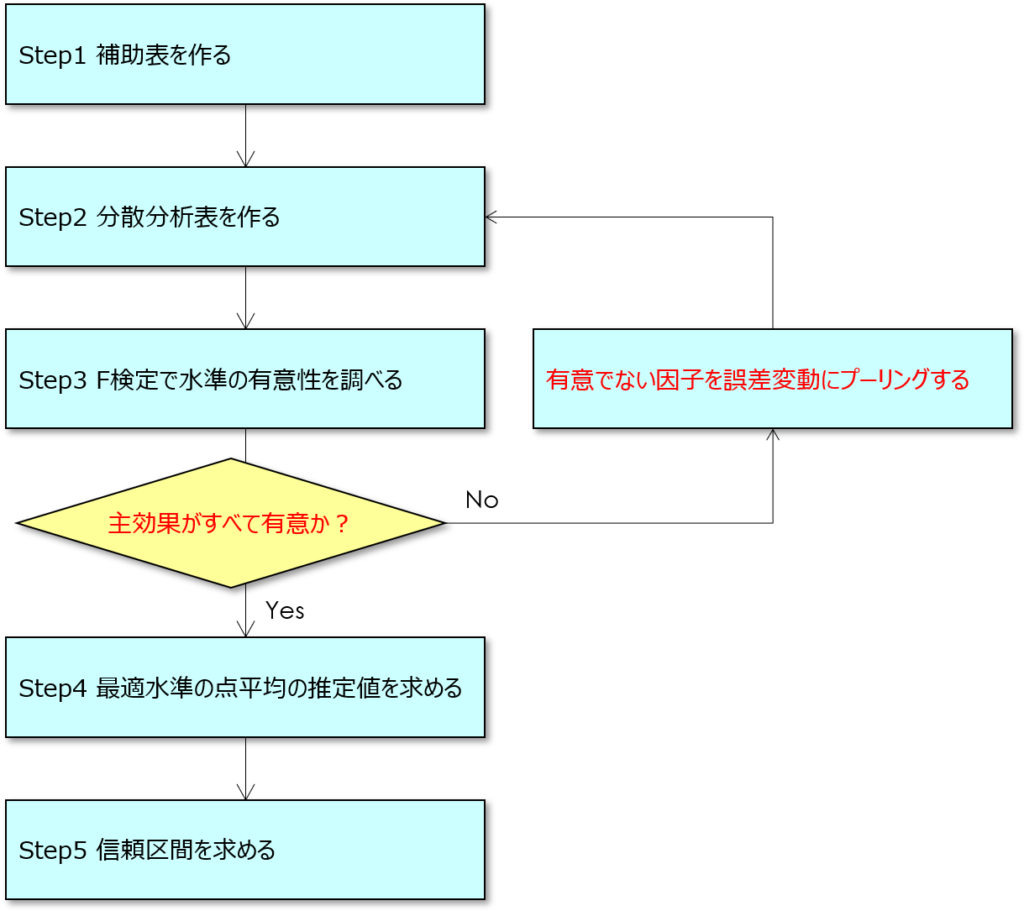
黒い文字で示すのは一元配置実験と同じ項目で、赤い文字で示すのが二元配置実験で新たに登場する手順です。
因子が二つになったことで、因子の主効果や交互作用が有意でないと判定された場合には、誤差成分にまとめる「プーリング」と呼ばれる処理が発生します。
ただ、ここに示した大まかな流れは、繰り返しの有無によらず共通ですので、特に違いはありません。
後ほど詳しく説明しますが、交互作用の水準間変動の計算のしかた、最適水準の点平均の求め方が、繰り返しの有無によって異なります。

同じ点と違う点を押さえて効率よく覚えよう
分散分析のやり方
それでは、具体例を用いて実際に分散分析表を作り、信頼区間の導出までやってみましょう。
交互作用が有意な場合と有意でない場合によって、分散分析表の完成形が異なりますので、それぞれに対して具体例を用いて手順を説明します。
交互作用が有意な場合
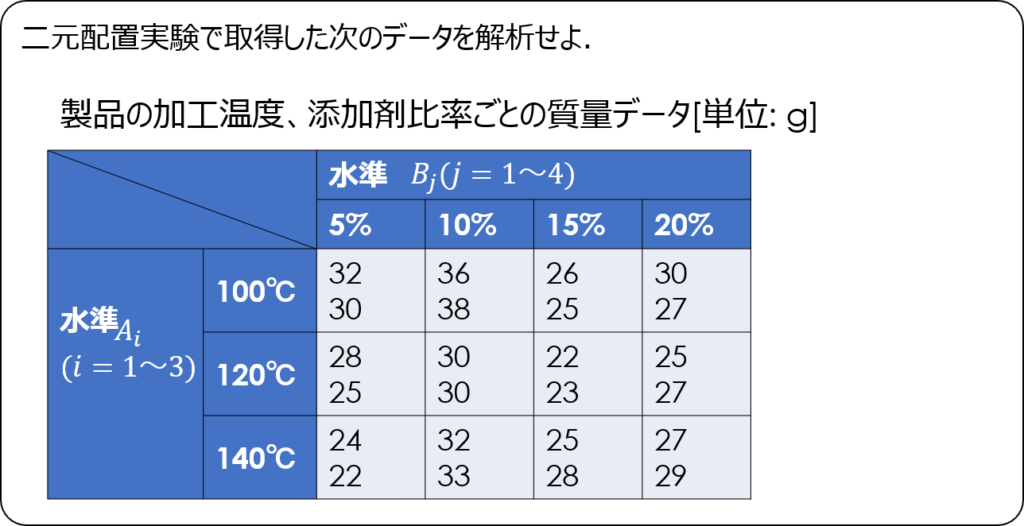
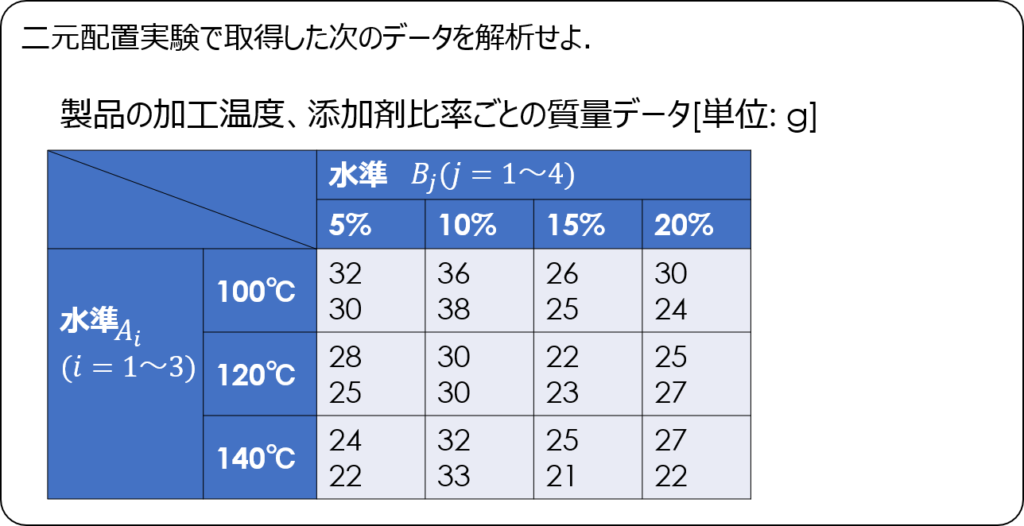
水準ごとの二乗の和を求める
偏差平方和を求める前に補助表を作成します。
必要な項目としては、水準ごとのデータの和、二乗の和で、繰り返しの無い場合と基本的には同じです。
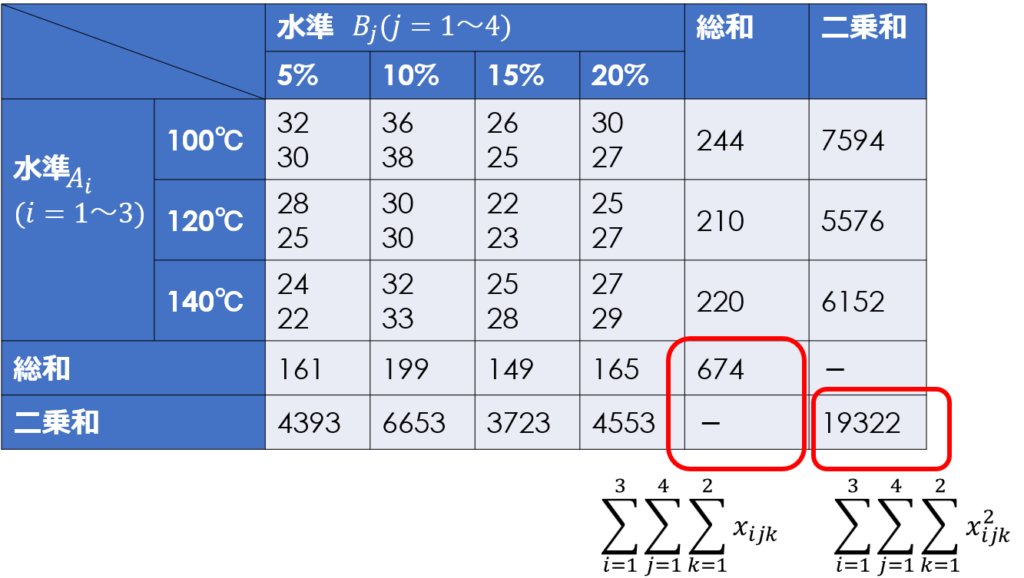
ひとつ計算が増える点としては、繰り返し回数分を合計したデータ表を用意したほうが望ましいことです。
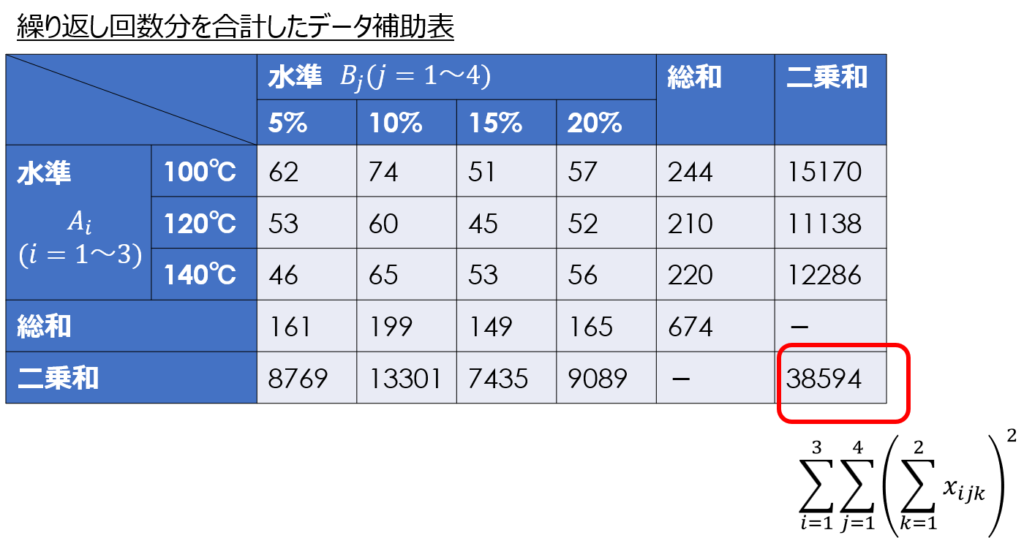
二元配置実験では、一元配置と比べて条件の通り数が多く、さらに繰り返しも含めるとデータ数が非常に多くなります。
その分、計算ミスもしやすいため、個々のデータの合算は暗算レベルでできるとしても、途中でやり直しができるよう、補助表を準備しておくことが望ましいです。
エクセルで計算する場合でも、偏差平方和の計算をひとつのセルだけで行うのは関数が長くなるので、繰り返し回数分の合計値は別のデータ表を準備することをおススメします。
偏差平方和、自由度、分散(平均平方)、分散比を求める
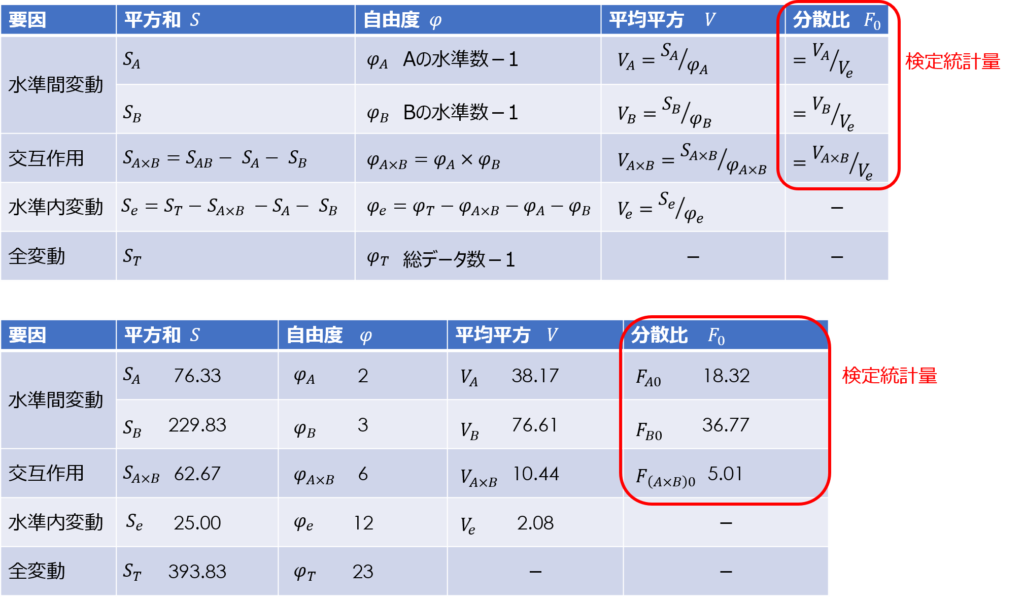
補助表の値を使って、分散分析表を埋めていきます。
全変動の偏差平方和$S_{T}$は次の式で求められます。

また、水準間変動の偏差平方和$S_{A},S_{B}$は定義の式を変換して、次の式で求められます。

次に交互作用$S_{A×B}$ですが、これは偏差平方和から直接求めることができず、次の関係式を用いて計算します。
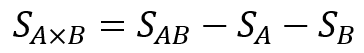
$S_{AB}$は因子Aと因子Bの組み合わせ条件に対する偏差平方和で、$S_{A}$や$S_{B}$と同様に水準ごとの平均値と全体平均との差の二乗から計算できます。

そして交互作用は、組み合わせ条件の変動$S_{AB}$のうち、主効果$S_{A}$や$S_{B}$で説明ができない残りの成分として、先ほどの式で定義されるのです。
今回の場合、$S_{A×B}$は次のように求められます。
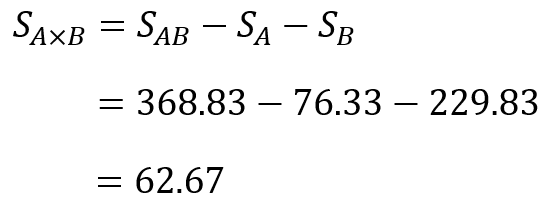
ここまで、偏差平方和の求め方が少し複雑でしたが、あとは、簡単な四則演算で表が埋められます。

電卓だと修正項を使わないと平方和の計算が大変だよ
F検定により有意性を判定する
分散比$F_{0}$を検定統計量として、F検定を行います。
判定基準となるF値は、自由度と有意水準が分かればF分布表から対応する値を読み取れば求められます。
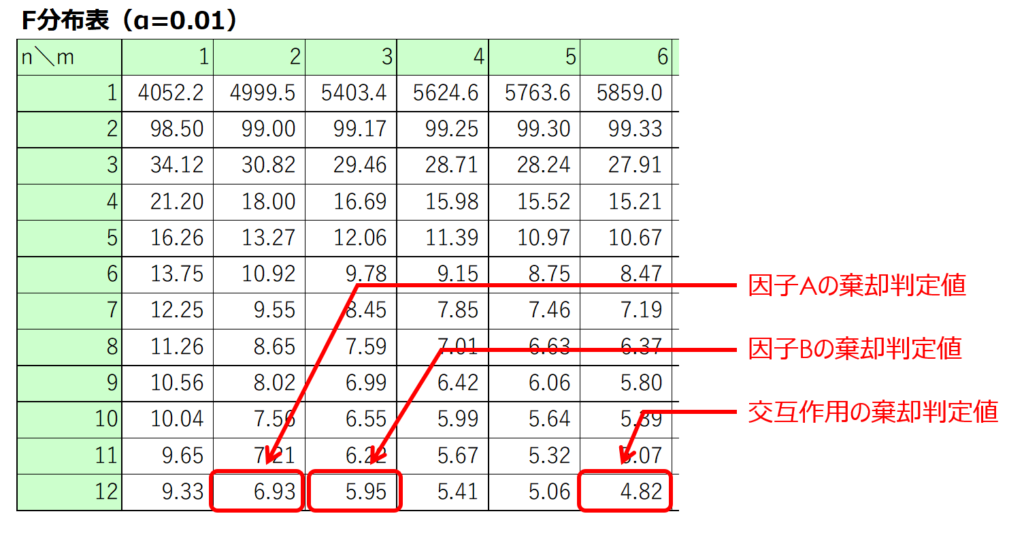
今回の場合、因子A、因子B、交互作用ともに有意水準1%で水準間変動に意味があるという結果が得られました。

誤差変動にプーリングする
今回は因子A、因子B、交互作用ともに有意であったため、プーリングは行いません。
仮にF検定により、いずれかの因子が有意でない、かつ$F_{0}$の値が2以下という結果が得られた場合には、特性に寄与しないものと判断し、誤差成分として一つにまとめてしまいます。
この時、分散比とF検定の棄却判定値が変わるので、プーリング後の分散分析表から再度$F_{0}$の値を検定し直します。
最適水準の点平均の推定値を求める
因子の有意性の判定が終わったら、次に最適水準の点平均の推定値を求めます。
今回の場合、特性値が大きいほど良いとして、質量が最大となる水準の推定値を求めます。
繰り返しのない二元配置実験では、因子Aと因子Bのそれぞれに対して特性値が最大となる水準を決め、以下の式で点平均の推定値を求めました。
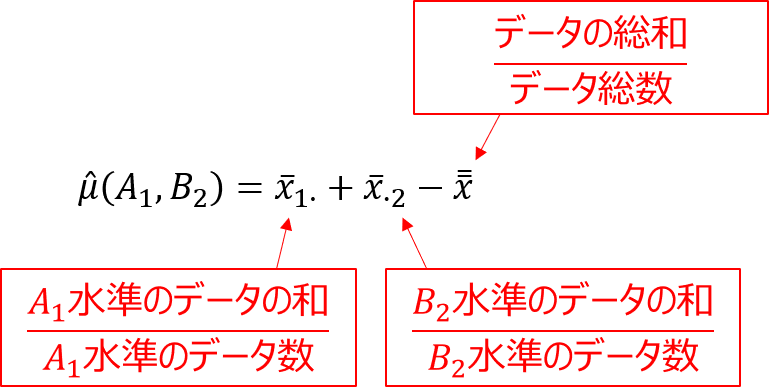
交互作用のある繰り返し実験では、因子Aと因子Bの組み合わせによって特性への影響の大きさが変わってくるので、この方法では効果を正しく反映できません。
結論を言うと、むしろ交互作用がある場合の最適水準はシンプルで、ずばり特性値が最大となる水準の繰り返しデータを平均したものが点平均の推定値となります。
信頼区間を求める
信頼区間は以下の式で求めることができます。

実験計画法に限らず、統計的推定でも基本的にはこの形の式しか登場しませんので、何度も復習して覚えてしまいましょう。
交互作用のある場合、誤差分散を繰り返し回数で割ります。
今回の場合、以下のように信頼区間を計算できました。
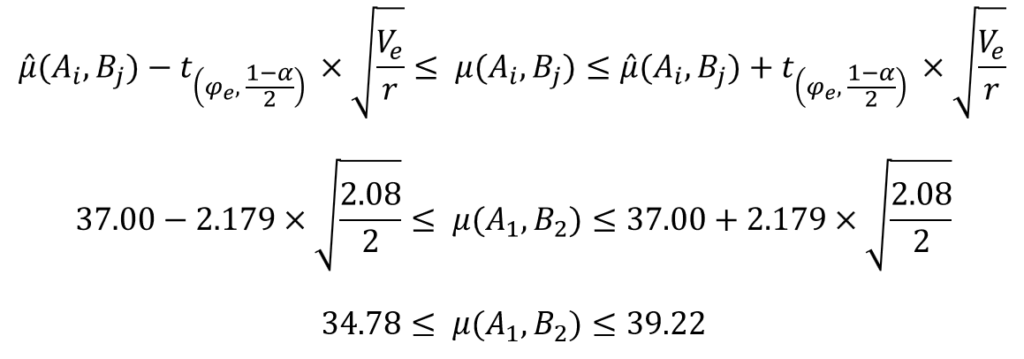
交互作用が有意でない場合
次に交互作用が有意でない場合の解析方法を説明します。
偏差平方和から分散分析表を作成してF検定で判定するところまで、交互作用のある場合と同じ手順なので割愛します。
誤差変動にプーリングする
交互作用が有意でない場合、誤差成分に含めてプーリングします。
プーリングのしかたは簡単で、偏差平方和と自由度をそのまま誤差成分に加算すればよいのです。
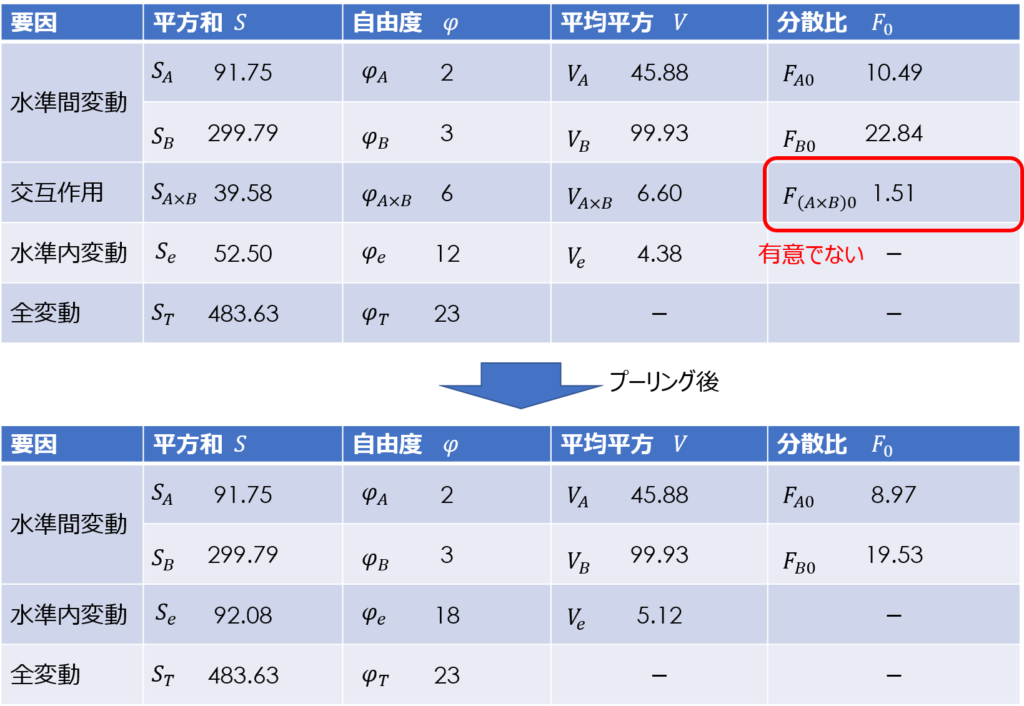
あとは、プーリング後の誤差成分の偏差平方和と自由度をもとに、誤差分散と各成分の分散比を再計算します。
検定統計量である分散比と棄却判定値が変わるので、再度F検定による有意性の判定を行います。

最適水準の点平均の推定値を求める
交互作用を無視できる場合の最適水準は、繰り返しのない二元配置実験と同様に、以下の式で求めることができます。
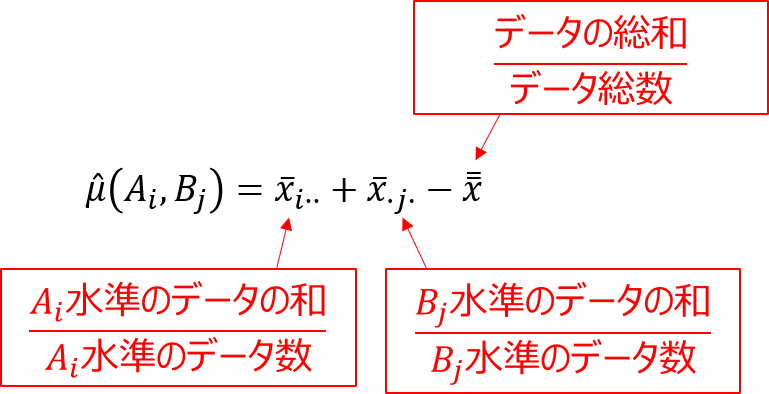
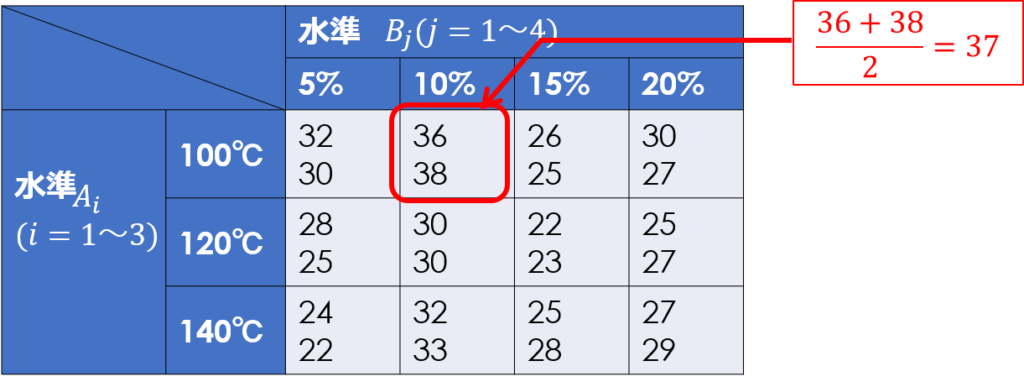
今回の場合、因子Aは水準1(100℃)、因子Bは水準2(10%)が最も特性値が大きくなっています。
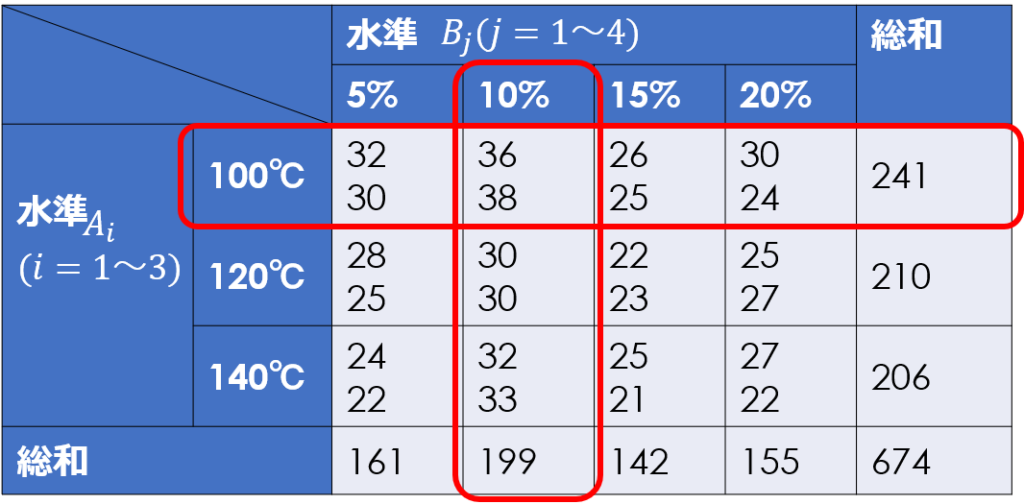
そして、各因子の最適水準を決定したら、以下の式により$x_{12}$の点平均の推定値を計算します。
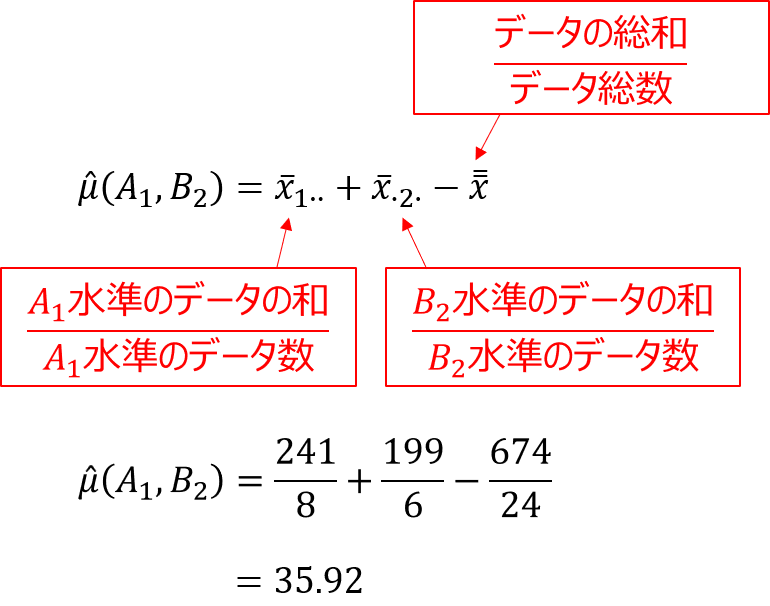

組み合わせ数が多くて複雑なら、まず繰り返しなしから練習しよう
信頼区間を求める
信頼区間に関しても、繰り返しのない二元配置実験と同じ方法で求められます。

有効反復数($n_{e}$)は以下の式を用いて求めます。
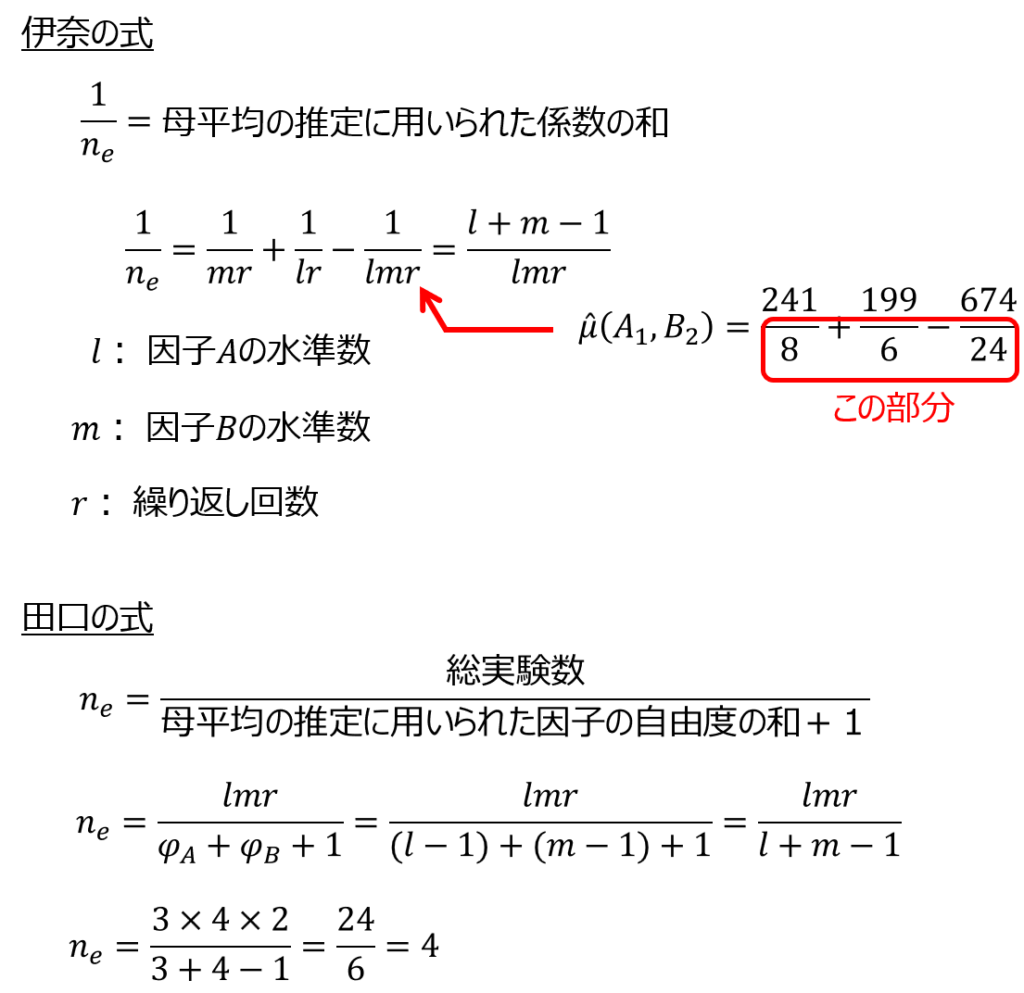
あとは、自由度と有意水準に対応するt値をt分布表もしくはエクセル関数などを用いて求めれば、信頼区間を算出することができます。
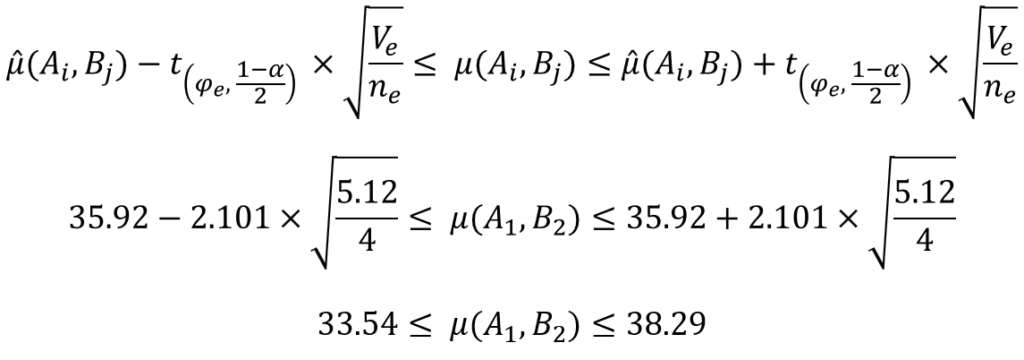
まとめ
繰り返しのない二元配置実験、繰り返しのある二元配置実験(交互作用あり・なし)の違いをまとめると次のようになります。
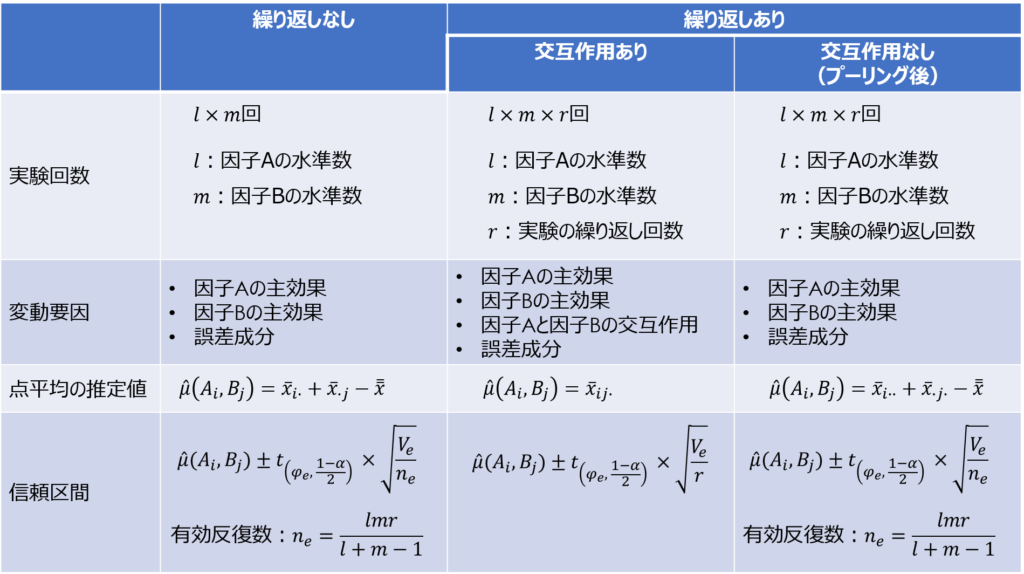
基本的な考え方や解析の流れは同じですが、点平均の推定値や有効反復数の計算のしかたが異なります。
それぞれ、セットで特徴を押さえておいて、目的の実験に応じた適切な手法を選べるようにしておきましょう。
最後までご覧いただきありがとうございました。
数式の苦手な方でも安心の入門編。
回帰分析、検定、実験計画法まで幅広く、エクセルを用いた実践方法も習得したい方に。
乱塊法、分割法もお任せ! QC検定1級の教材としてもおススメ。




コメント