「計数規準型って何? どういう考え方の検査なの?」
「検査表が複雑そうで、読み方が分からない」
「とにかく例題で$n$と$c$の求め方の流れを理解したい」
このような疑問や悩みをお持ちの方に向けた記事です。
計数規準型抜取検査は、とあるロットからサンプルを抜き取って、不適合品の個数でロットの合否を判定する検査で、最も基本的な抜取検査の手法の一つです。
個数のみで判定できることから運用面からみてもシンプルで分かりやすく、抜取検査を設計する上では、必ず理解しておきたい手法です。
この記事では、計数規準型抜取検査の特徴と実施の手順、抜取検査表からサンプルサイズと合格判定個数を読み取る方法について例題を用いて解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
計数規準型抜取検査とは
生産者危険と消費者危険
計数規準型の説明に入る前に、抜取検査の特徴をおさらいしておきましょう。
抜取検査は、全数検査と比べて検査にかかるコストを抑えられ、さらに破壊試験も適用できる利点があり、主に量産品の検査として広く活用されています。
その一方で、確率計算に基づいてロットの合格/不合格を判定する性質から、本来は不合格とすべき品質の悪いロットを合格と判定して出荷してしまう「見逃しリスク」が伴います。
これを消費者危険と呼び、$β$として表記されます。
JIS Z 9002-1956(計数規準型一回抜取検査)によると、$β$を0.10として設定されています。
また反対に、本来は合格とすべきロットを不合格にして出荷を取りやめる「見過ぎリスク」のケースもあり、この場合は生産者側のリスクとして織り込んでおかねばなりません。
これを生産者危険と呼び、$α$を0.05として設定されています。
計数規準型抜取検査の考え方
計数規準型抜取検査は、売り手(生産者)に対する保護と買い手(消費者)に対する保護を考慮して、両者の要求を満足する検査規準を設定する検査です。

抽象的で何だかよくわからない
売り手に対する保護というのは、先ほど説明した生産者危険のことを意味しています。
本来は合格とすべきロットを厳しく検査し過ぎたせいで不合格と判定する確率が増えると、生産者は損をすることになります。
例えば、$α$を0.2などに設定すると、誤判定で不合格とする確率を20%まで許容することになってしまいます。
そのため、生産者を保護する目的で$α$をある一定以下の小さな値にあらかじめ設定しているのです。
同様に買い手に対しては、検査を緩くし過ぎると不合格品を手にする消費者にとっては損をすることになります。
そのため、消費者を保護する目的で$β$も一定以下の値に設定しています。
売り手と買い手の双方の要求とは、$α$と$β$の値に加えて、それぞれに対応する不適合品率$p_{0}$と$p_{1}$を規定することも含まれます。
$α$と$β$の値だけでは、不適合品率が何パーセントの場合におけるか次第で、厳しさの具合が変わってきます。
そのため、生産者危険として不適合品率$p_{0}$における$α$(0.05)、消費者危険として$p_{1}$における$β$(0.10)という風に対応付けることで初めて、双方の要求が定義されるのです。
そして、この要求を満足できる検査の規準として、JISで規定された抜取検査表を用いて、$α,β,p_{0},p_{1}$に対応するサンプルサイズと合格判定個数を設定するのです。
なお、抜取検査の基本的な考え方や種類については、以下の記事で詳しく解説していますので、合わせてご覧ください。

計数規準型一回抜取検査の手順
次に計数規準型抜取検査の手順について説明します。
抜取検査の回数としては、一回で合否を判定する一回検査と、一回目に合格基準を満たさなかった場合に二回目を実施する二回検査の二種類があります。
計数規準型抜取検査では、一回が基本となりますので、ここでは一回検査での実施手順について説明します。
一連の流れをざっくり記載すると次のようになります。
- $p_{0}$と$p_{1}$を設定する
- サンプルサイズ$n$と合格判定個数$c$を決める
- ロットからサンプルを採取して検査する
- 合格・不合格の判定を下す
$p_{0}$と$p_{1}$を設定する
まずは先ほどにも説明したように、売り手と買い手の双方の要求を数値化します。
客先の相手が限定されて明確な場合には、後々のトラブルの未然防止として、あらかじめ客先と合意を取って決めることも多くあります。
生産能力や経済的事情、検査に要する労力や時間など、諸々の事情を考慮して設定することが望ましいです。
サンプルサイズ$n$と合格判定個数$c$を決める
JIS Z 2002-1956の抜取検査表を用いて、$n$と$c$を決めます。
表の読み取り方は後述しますが、$p_{0}$と$p_{1}$に対応する$n$と$c$の値が割り振られているので、機械的に読み取るだけで大丈夫です。
ロットからサンプルを採取して検査する
抜き取りの個数と合否判定が明確になったら、ロットからサンプルを採取して検査します。
ロットの編成にあたっては、同一条件で製造されたものが品質ばらつきを抑える観点でも好ましく、さらには同一設備であると一層とばらつきを低減できます。
ただし、全ての条件を固定して、あまりにロットを細かくしすぎると、検査コストが増えてしまうので注意が必要です。
反対にロットの単位が大きすぎる場合には、ロット内に異なる傾向の分布が存在する可能性もあるので、確率論で議論するにあたって適切でない場合もあります。
これらの背景を考慮して、適切なロットサイズを設定して運用しましょう。
ロットの合格・不合格の判定を下す
抜き取ったサンプルひとつずつに対して合格・不合格を判定し、合否の数を集計します。
不適合品の数が合格判定個数$c$以下であれば、そのロットを合格と判定します。

判定がシンプルで分かりやすいね
OC曲線
OC曲線とは
抜取検査を行うにあたって、OC曲線というグラフをご存じでしょうか。
OC曲線(Operating Characteristic Curve)は検査特性曲線とも呼ばれ、サンプルサイズや合格判定個数の妥当性、ロットの合否判定の見誤りリスクを数値化する上で活躍するグラフです。
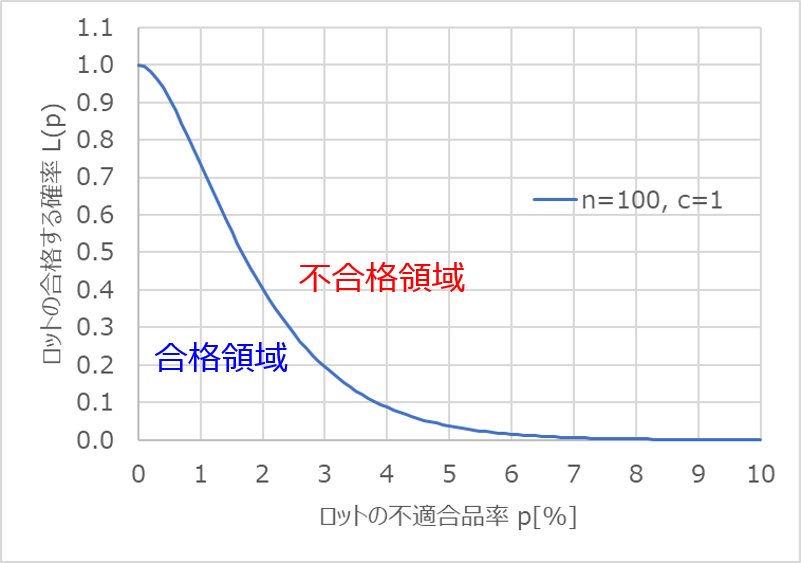
横軸にはロットの不適合品率$p$(不良率)をパーセント表記で、縦軸にはそのロットが合格と判定される確率$L(p)$を取ります。
つまり、とある不適合品率のロットを抜取検査した場合に合格と判定される確率を表したもので、連続的に描かれた曲線から任意の$p$における$L(p)$の値を読み取ることができます。
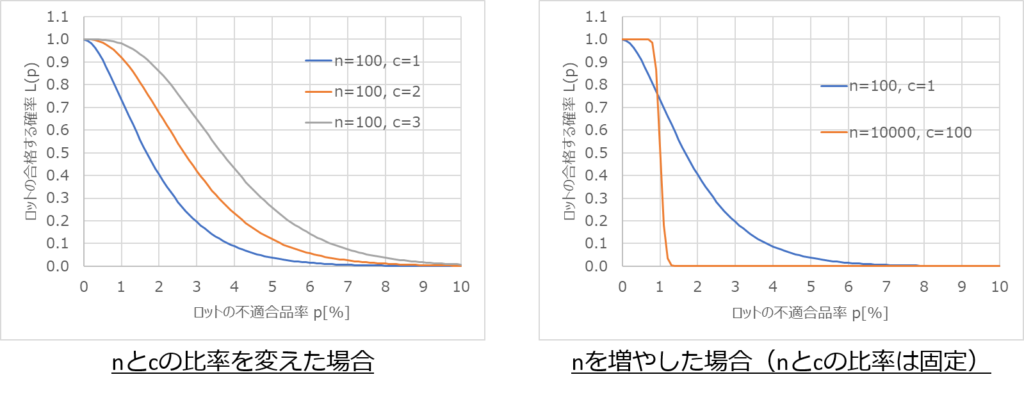
なお、抜取検査の厳しさの具合によってロットの合格率が変わるので、OC曲線はサンプルサイズ$n$と合格判定個数$c$の値によって横方向にシフトしたり、傾斜が変わったりします。
OC曲線を用いるメリット
ひとつめのメリットは、$p$と$L(p)$に対して任意の値を求められることです。
OC曲線において、$L(p)=0.95$は生産者危険、$L(p)=0.10$は消費者危険を表します。
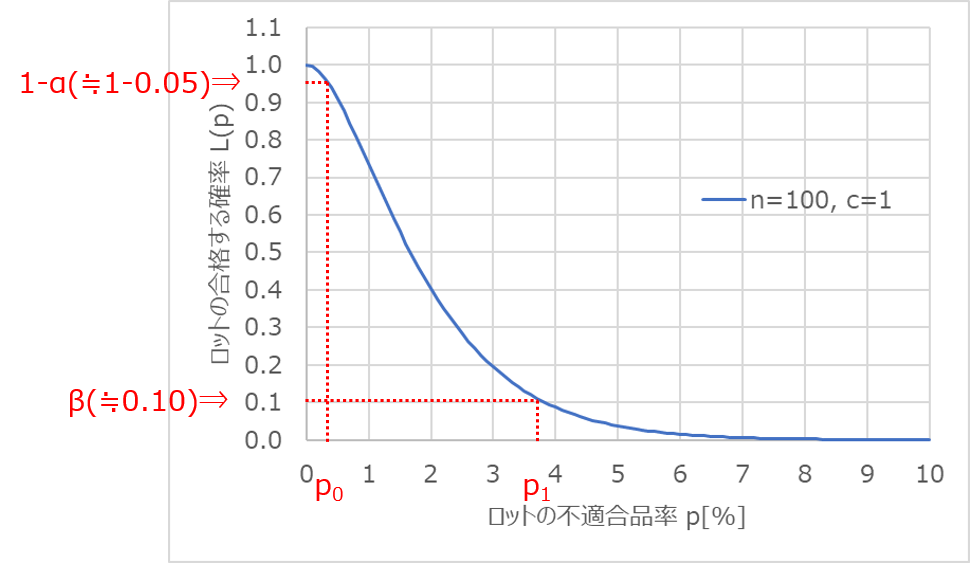
この時の対応する$p$の値が、あらかじめ設定した$p_{0}$と$p_{1}$になるのは、まさにその通りなのですが、連続する曲線では任意の値を読み取ることができます。
例えば、ロットの合否判定の見誤りをなるべく減らしたい場合、$p_{0}$と$p_{1}$の値をできるだけ近づけて設定することが必要となります。
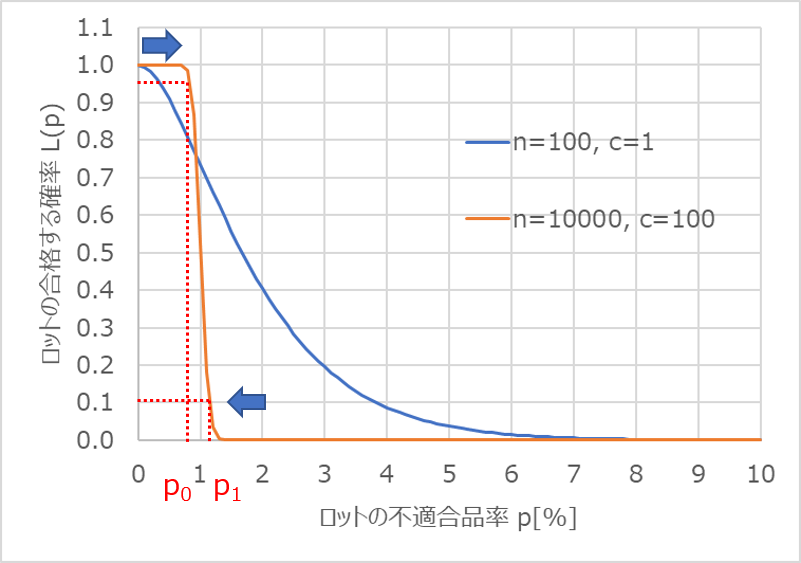
ただし、このようなOC曲線の形状にするには、サンプルサイズを多く採る必要があり、経済的には好ましくありません。
そのため、現状のOC曲線において$p_{0}$から$p_{1}$の間のグレーゾーンの不適合品率のロットがどの程度の合格率なのか把握しておくことで、適切な$n$と$c$の設定に役立ちます。
ふたつめのメリットとしては、抜取検査表にない$n$と$c$の組合せについても確率を求められることです。
OC曲線は、$n$と$c$、および不適合品率$p$の値から、二項分布の式をもとに計算しています。
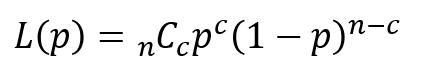
そのため、任意の値を自分で設定してOC曲線を作成することも可能で、サンプルサイズに制約のある場合などに用いると有効です。
なお、OC曲線の読み方や確率計算の方法については、以下の記事で詳しく解説していますので、合わせてご覧ください。

抜取検査表の読みかた
ここまで生産者危険と消費者危険について説明してきました。
実は、これらの内容を理解できていると、抜取検査表の読みかたは直感的であり、非常に簡単なものです。
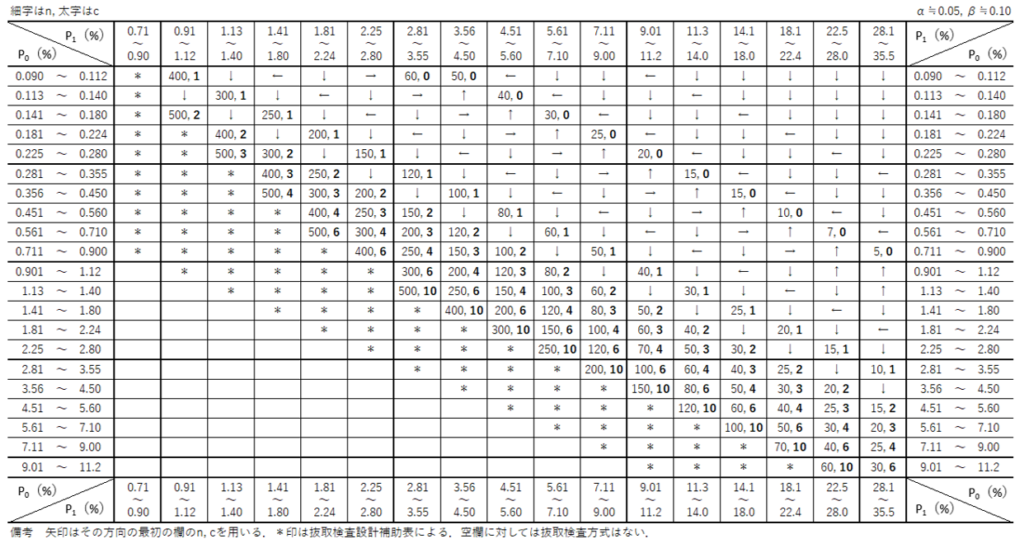
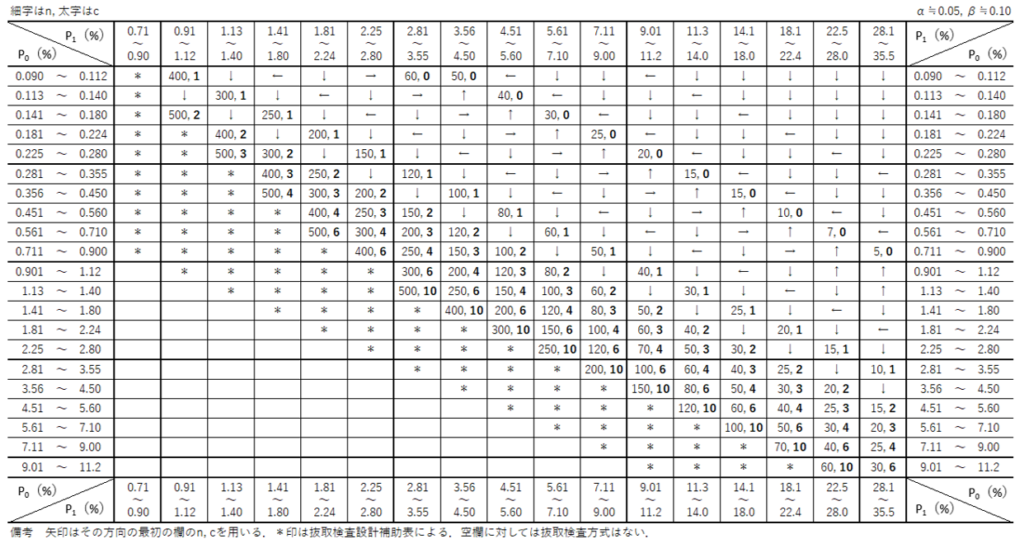
あらためて、抜取検査表を次に示します。
見ての通り、縦軸には$p_{0}$、横軸には$p_{1}$が割り振られており、これらの値の交差する箇所に二つの数値もしくは矢印、「*」印が記載されています。
読み取り方は簡単で、設定した$p_{0}$と$p_{1}$に該当するセルから交差する箇所の値を読み取るだけです。
細字は$n$、太字は$c$を表すので、例えば$p_{0}=1.0$、$p_{1}=6.0$の場合、$(n,c)=(80,2)$と読み取れます。
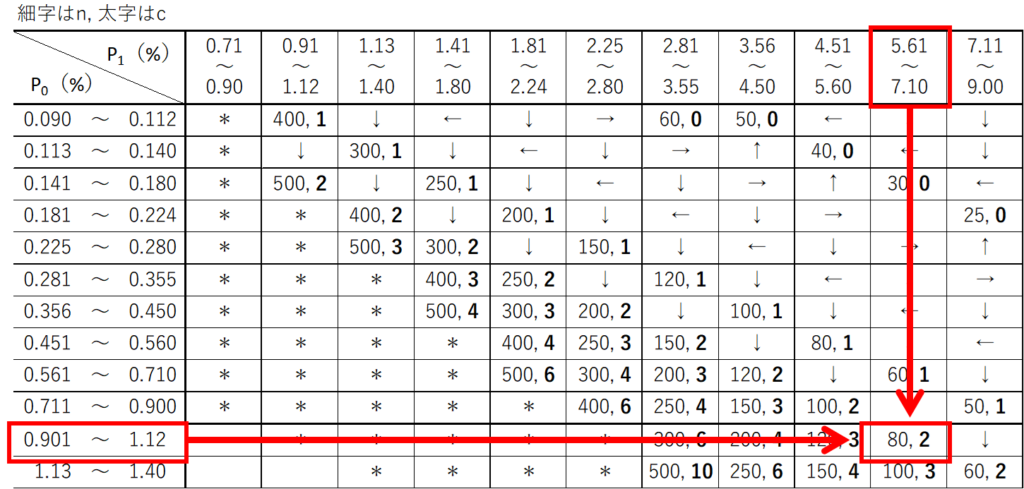
つまり、80個のサンプルを抜き取って、不適合品が2個以下であれば、ロットを合格と判定するということです。
なお、数値が割り振られていない箇所は、矢印に示す向きに進んで数値の記載されたセルにたどり着いた箇所の値を適用します。
また、「*」と記載された箇所は、以下に示す抜取検査設計補助表から計算して求めます。
なお、空欄のセルに関しては、そもそも抜取検査として成立しておらず、値が存在しません。
これらは、$p_{0}>p_{1}$となっており、生産者危険の方が消費者危険よりも高いという、矛盾した状況になっており、そもそも抜取検査の定義に反します。
例題
では、実際にいくつかのケースを題材に、$n$と$c$の値を読み取ってみましょう。
例題1($p_{0}=0.4$%, $p_{1}=4.0$%)
これは単純に行と列の交差する箇所を読み取れば良いので簡単ですね。
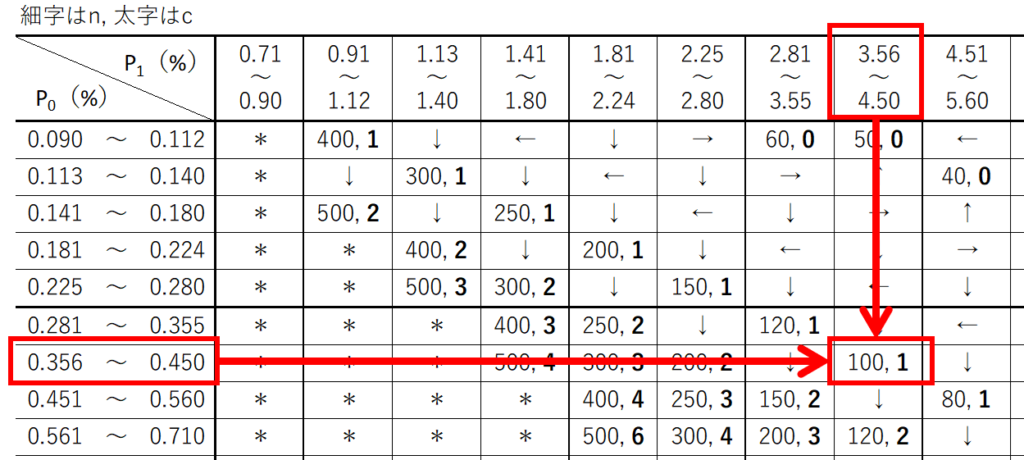
$n=100, c=1$と求められます。
例題2($p_{0}=0.25$%, $p_{1}=5.0$%)
行と列の交差する箇所には「↓」の矢印が記載されています。
この矢印の示す方向とたどっていくと、(100,1)に当たります。
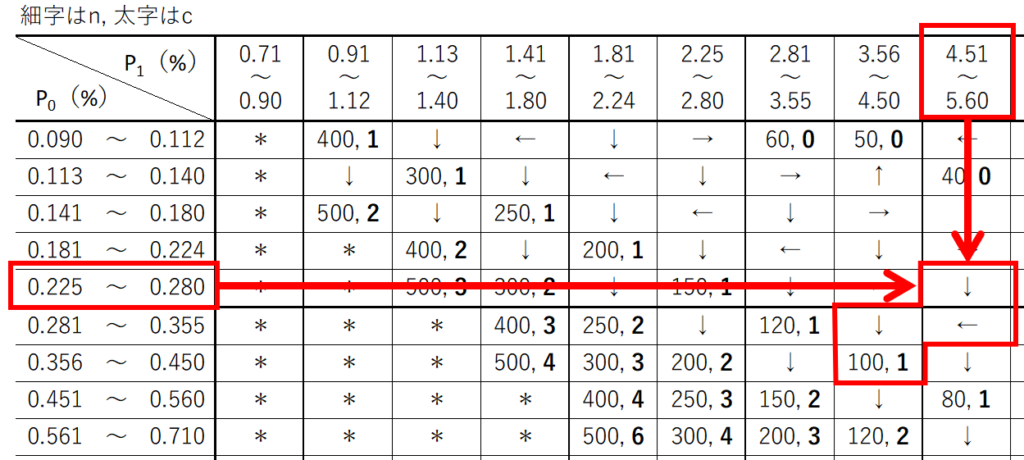
すなわち、$n=100, c=1$と求められます。
例題3($p_{0}=0.5$%, $p_{1}=1.2$%)
行と列の交差する箇所に「*」の記載があるので補助表を用います。
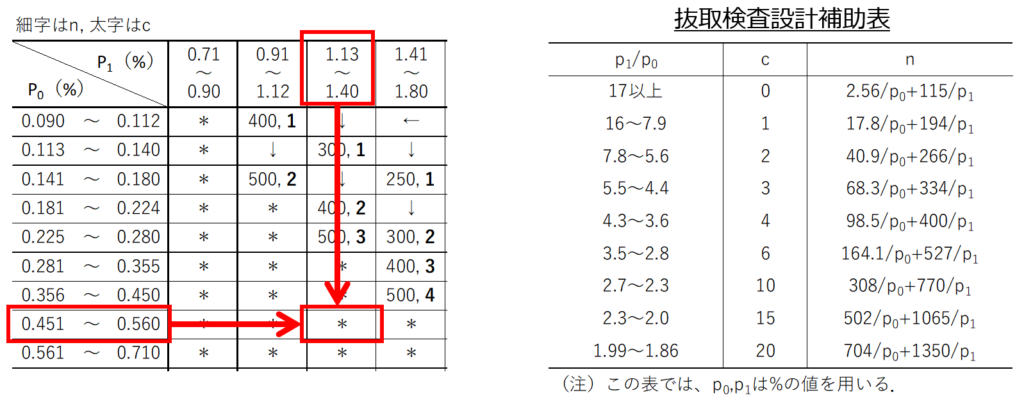
$n$の値は補助表の計算式から以下のように求められます。
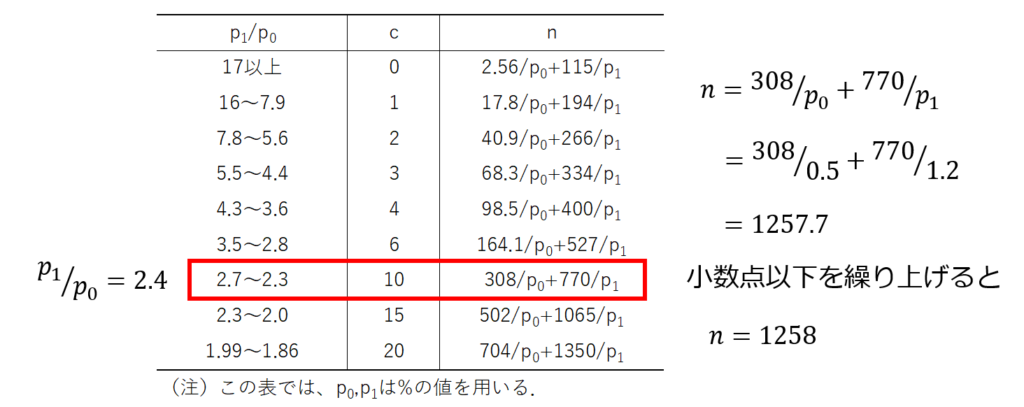
すなわち、$n=1258,c=10$と求められます。

p0とp1の値が近いってことは、たくさん検査しないと保証できないんだね
まとめ
- 計数規準型抜取検査
不適合品の個数でロットの合否を判定する検査
売り手(生産者)と買い手(消費者)に対する保護を考慮して、両者の要求を満足する規準を設定 - 計数規準型一回抜取検査の手順
①:$p_{0}$と$p_{1}$を設定する
②:サンプルサイズ$n$と合格判定個数$c$を決める
③:ロットからサンプルを採取して検査する
④:合格・不合格の判定を下す - OC曲線
サンプルサイズや合格判定個数の妥当性、ロットの合否判定の見誤りリスクを調べるための確率グラフ
横軸:ロットの不適合品率$p$(不良率)、縦軸:合格と判定される確率$L(p)$ - 抜取検査表の読みかた
$p_{0}$と$p_{1}$の値の交差する箇所の$n$と$c$の値を読み取る
矢印の記載がある場合は向きをたどって到達した値を適用する
「*」の記載がある場合は補助表を用いて計算する
最後までご覧いただきありがとうございました。
抜取検査のエッセンスが詰まった本はズバリこれ
QC検定2級対策として、計数規準型抜取検査、計量規準型抜取検査を効率よく学習したい方はこちら
QC検定1級対策として、選別型抜取検査、調整型抜取検査を効率よく学習したい方はこちら




コメント