「計量規準型ってどういう考え方? 計数規準型との違いは?」
「JIS規格にいろんな種類の検査があって良くわからない」
「正規分布のグラフと記号がいっぱい登場してギブアップ・・」
このような疑問や悩みをお持ちの方に向けた記事です。
計量規準型抜取検査は、とあるロットから抜き取ったサンプルの計量値を取得し、平均値と標準偏差から合否を判定する検査で、最も基本的な抜取検査の手法の一つです。
標準偏差や合格判定値、上下限規格など多くの記号や数値が登場し、さらには標準偏差が既知と未知の場合で計算式が異なるなど、初心者の方には難しく感じるかもしれません。
ただ、細かい分類がいくつかあっても基本的に考え方は同じであり、合格判定値と上下限規格との関係性も図のイメージとしてとらえておけば意外と簡単なものです。
この記事では、計量規準型抜取検査の種類と実施の手順、抜取検査を設計するにあたって理解しておきたい考え方について解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
計量規準型抜取検査とは
計量規準型抜取検査は、とあるロットから抜き取ったサンプルの計量値を取得し、平均値と標準偏差から合否を判定する検査です。
「計量」とは量ることのできるものを意味し、重さや寸法などの項目が該当します。
また、計量と対する用語として「計数」があり、こちらは数えることのできるものとして、不適合品の数などが該当します。
計数規準型抜取検査では、抜き取ったサンプルの不適合品の個数からロットの合否を判定します。
計数型のメリットとしては、個数で合否を判定できることから、考え方や運用がとても単純なことが挙げられます。
例えば、ロットからサンプルを100個抜き取って、不適合品が1個以下なら合格、2個以上なら不合格とすれば、計算も不要で間違えようもないですね。
一方、計量規準型抜取検査のメリットとしては、計数型と比べて検査に必要なサンプル数を減らすことができる点です。
特に、標準偏差が既知の場合、すなわち計量値の分布がすでに分かっている場合には、統計量として意味のある平均値を取得できれば良いので、サンプル数を大幅に減らせます。
ここで一つ注意事項として、平均値と標準偏差を扱う特性上、計量規準型抜取検査は正規分布を仮定できる場合に限るので、その前提を忘れないようにしましょう。
以上のように、計量型と計数型のそれぞれメリットがあるので、特長を把握して状況に応じて適切な方式を使い分けられることが望ましいです。
なお、計数規準型抜取検査については、以下の記事で詳しく解説していますので、合わせてご覧ください。

計量規準型抜取検査の種類
計量規準型抜取検査にはいくつかの種類があり、保証の対象、標準偏差の既知・未知によって次のように分類されます。

保証の対象による分類
ロットの平均値を保証する場合と、ロットの不適合品率を保証する場合に分けられます。

平均値を「保証」ってどういうこと
「保証の対象」というと難しく感じるかもしれませんが、平均値と不適合品率のどちらを規定したいのか、という意味と捉えれば分かりやすいかもしれません。
例えば、たまごの質量を品質特性として検査しているとします。
質量の平均値が60g以上のロットはなるべく合格、55g以下のロットはなるべく不合格にしたい、といったように平均値の指標が明確な場合に、平均値を保証する方式を用います。
一方、不適合品率が0.5%以下の良いロットはなるべく合格、5%以上の悪いロットはなるべく不合格といった指標が明確な場合に、不適合品率を保証する方式を用います。
標準偏差の既知・未知による分類
もう一つの分類として、検査するロットの標準偏差の既知・未知による分け方があります。
標準偏差が既知の場合はJIS Z 9003-1979(計量規準型一回抜取検査:σ既知)、未知の場合はJIS Z 9004-1983(計量規準型一回抜取検査:σ未知)にて詳細が規定されています。
ここで、これから検査する対象のロットの標準偏差なんて既知のはずないじゃないか、という素朴な疑問が思い浮かぶかもしれませんが、厳密にはその通りです。
ただ、これまでに膨大な検査データの蓄積があって、母集団の標準偏差として扱えるほど十分な裏付けのある場合には、過去データから標準偏差を既知とみなすこともできます。
この場合、既に分布のばらつきが分かっていることから、抜き取りのサンプル数を減らすことができます。
一方、標準偏差が未知の場合には、抜き取ったサンプルそのものから標準偏差を求める必要があります。
そのため、既知の場合と比べて、抜き取りサンプル数が多くなる性質があります。
抜取検査そのものの負担は標準偏差が未知の場合のほうが大きいですが、十分なバックデータがなくてもロットの合否を判定できる利点もあります。
平均値を保証する検査の設計と手順
計量規準型抜取検査の特徴と種類が理解できたところで、次は検査を設計するにあたっての考え方を説明します。
なお、平均値の低い方が好ましい場合と高い方が好ましい場合が想定されますが、基本的には同じ考え方ですので、ここでは低い方が好ましい場合を前提として説明します。
まず、平均値を保証する検査について、手順を示すと次のようになります。
- 平均値の指標$m_{0}$と$m_{1}$を設定する
- サンプルサイズ$n$と合格判定値を決める
- ロットからサンプルを採取して特性値を計測する
- 合格・不合格の判定を下す
平均値の指標$m_{0}$と$m_{1}$を設定する
まずは品質特性の指標を明確にします。
平均値の低い場合が好ましいということで、$m_{0}$以下のときは合格にしたいロット、$m_{1}$以上のときは不合格にしたいロットと定義し、$m_{0}$と$m_{1}$の数値を設定します。
サンプルサイズ$n$と合格判定値を決める
JIS Z 9003-1979の付表を用いて、サンプルサイズ$n$と合格判定値を決めるための係数$G_{0}$を求めます。
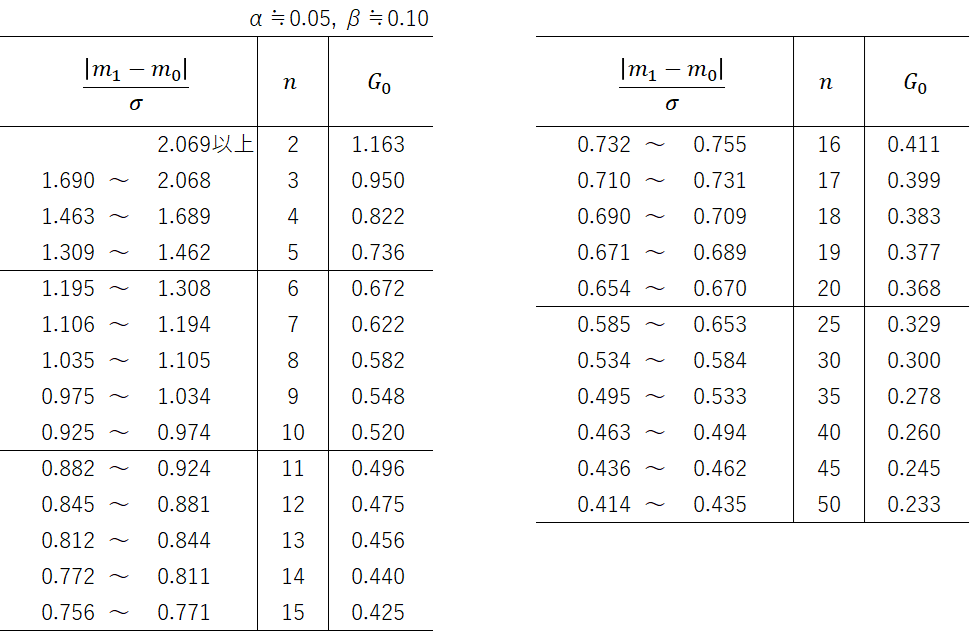
先ほどの$m_{0}$と$m_{1}$の値、ロットの標準偏差$σ$の値から、$n$と$G_{0}$を求めることができます。
表を見ても分かる通り、$(m_{1}-m_{0})/σ$の値の大きい方が、サンプルサイズ$n$が小さくなります。
$m_{1}$と$m_{0}$の差が大きいほどサンプル数が少なくて済むということであり、つまり合格・不合格にしたい指標が離れているほど、容易に判定ができることを意味しています。
あるいは、$σ$の値が小さく分布のばらつきが小さい場合でも、同様に少ないサンプルにすることができます。
ばらつきが小さいほど少ないサンプルでも判定がしやすくなることは、直感的にも理解いただけるかと思います。
ロットからサンプルを採取して特性値を計測する
サンプルを採取して特性値を計測し、得られた計測結果から平均値を求めます。
合格・不合格の判定を下す
合格判定値$\bar{X}_{u}$は次の式から求められます。
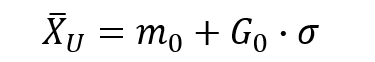
合格判定値$\bar{X}_{u}$とロットから取得した平均値$\bar{x}$を比較して、ロットの合否判定を下します。

計算も単純で意外と簡単だね
不適合品率を保証する検査の設計と手順
品質特性$x$の分布
ロットの不適合品率を保証する場合は、記号や用語が多く登場して混乱しがちなので、まずは良いロットと悪いロットの分布のイメージをつかむところから入りましょう。
以下は品質特性$x$の分布を表すイメージ図です。
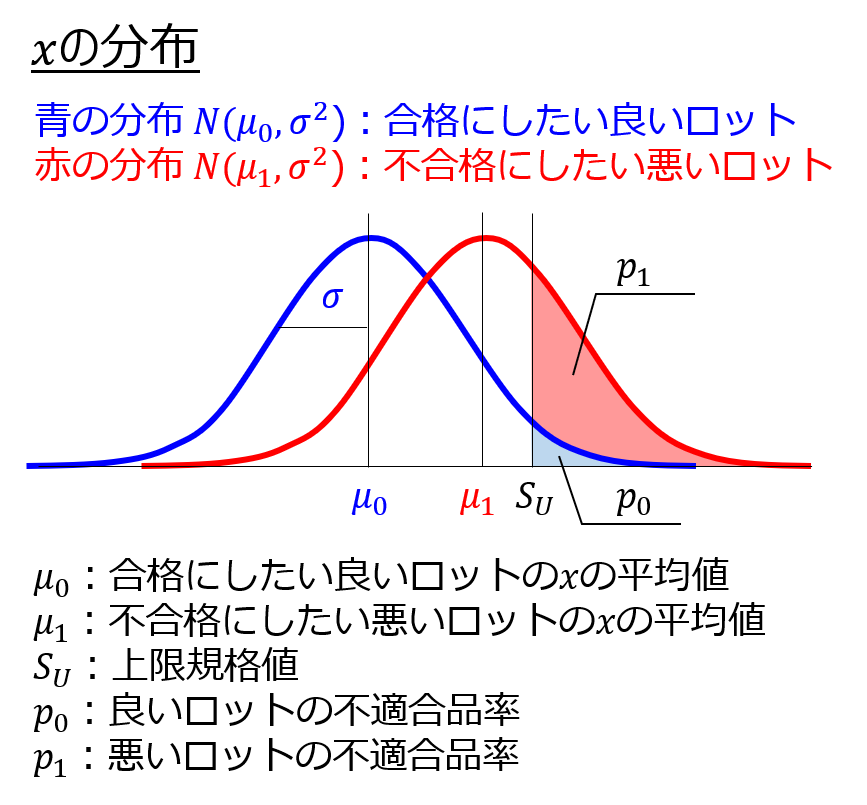
良いロット、悪いロットともに、上限規格値$S_{U}$($U$はupperの略)を超える不適合品が存在し、それぞれの確率を$p_{0}$と$p_{1}$と表記します。
この$p_{0}$と$p_{1}$が保証したい対象の指標となります。
ここで、元々の$x$の分布は単位系がまちまちで確率で議論できないので、標準正規分布の$K_{p}$値で比較できるよう正規化します。
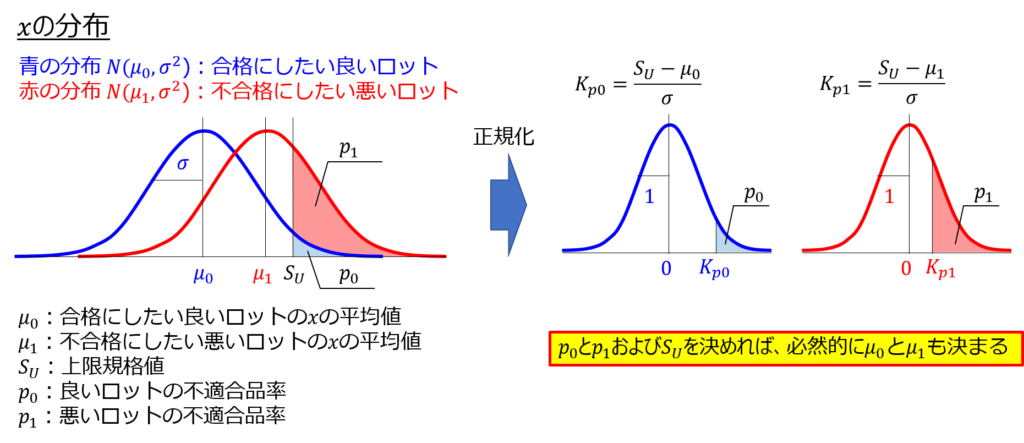
式を見て分かる通り、$p_{0}$と$p_{1}$、$S_{U}$を決めれば、必然的に$μ_{0}$と$μ_{1}$の値も決まります。
すなわち、所望の$p_{0}$と$p_{1}$を保証するためには、良いロットと悪いロットの品質特性の平均値がいくつである必要があるのか、一意的に定まるというわけなのです。
抜取サンプルの平均値の分布
次に抜取サンプルの平均値$\bar{x}$の分布のイメージを見てみましょう。
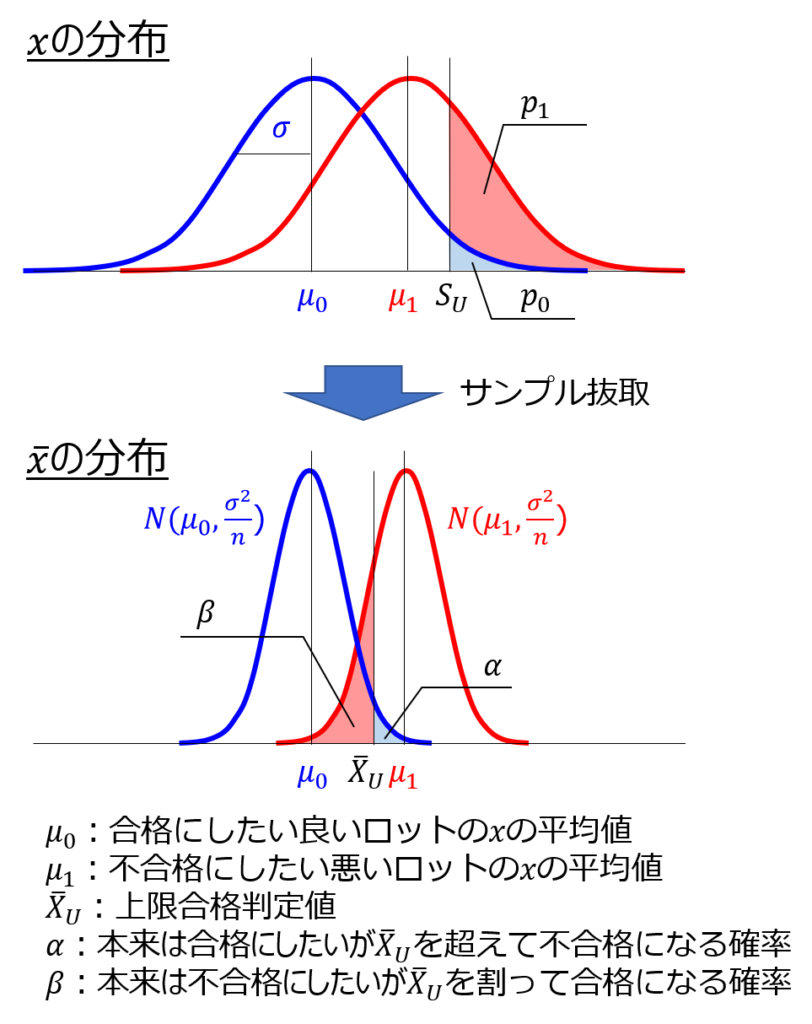
正規分布の定義から、母集団$N(μ_{0},σ^{2})$から抜き取ったサンプルの平均値は$N(μ_{0},σ^{2}/n)$に従います。
ここで、合格判定値$\bar{X}_{u}$を良いロットと悪いロットのピークの間に設定します。
図に示す通り、$α$は生産者危険(見過ぎのリスク≒0.05)、$β$は消費者危険(見落としのリスク≒0.10)として表現できます。
さらに、$\bar{x}$の分布についても正規化してみましょう。
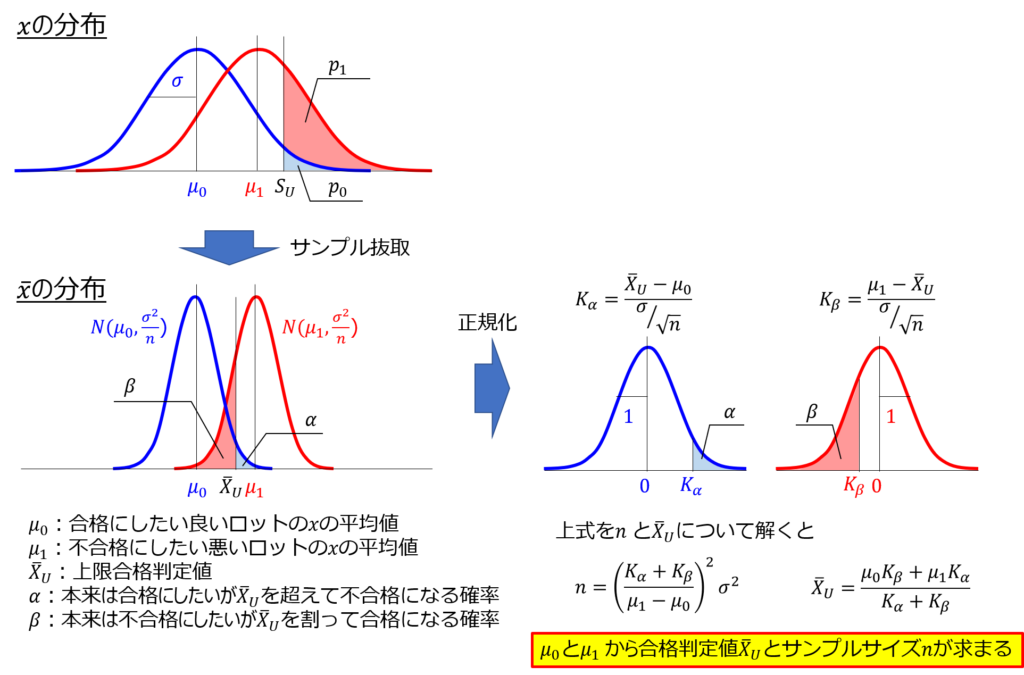
サンプルサイズ$n$と上限合格判定値$\bar{X}_{u}$は、$μ_{0}$と$μ_{1}$が決まれば計算できることが分かります。
ここでお気づきのかたも多いと思いますが、$μ_{0}$と$μ_{1}$は$S_{U}, p_{0}, p_{1}$から決まるので、結局のところ上限規格値と保証したい不適合品率から全てを求めることができるのです。
さて、予備知識を押さえたところで、手順について説明します。
一連の流れを記載すると次のようになります。
標準偏差$σ$が既知の場合と未知の場合で一部の計算方法が異なりますが、基本の流れはほぼ同じです。
- 上限規格値$S_{U}$(または$S_{L}$)を設定する
- 不適合品率の指標$p_{0}$と$p_{1}$を設定する
- サンプルサイズ$n$と合格判定係数$k$を決める
- ロットからサンプルを採取して特性値を計測する
- 合格・不合格の判定を下す
上限規格値$S_{U}$(または$S_{L}$)を設定する
上下限の規格を設定します。
片方の規格のみを対象とする場合には、必ずしも両方を設定する必要はありません。
不適合品率の指標$p_{0}$と$p_{1}$を設定する
保証したい不適合品率$p_{0}$と$p_{1}$を設定します。
先ほどのイメージ図から雰囲気が分かったと思いますが、抜取検査を設計するうえで、この指標を適切に設定するのが最も重要で、かつ最も難しいといっても過言ではありません。
平均値の保証の場合と同じく、$p_{0}$と$p_{1}$の値が近いほど良いロットと悪いロットを分離するのが困難になり、たくさんのサンプルを抜き取る必要が生じます。
一方で、$p_{0}$と$p_{1}$を離しすぎると、サンプルサイズは減らせますが、所望の精度で合否を分離することができません。
そのため、$p_{0}$と$p_{1}$の値は、合否判定の精度、検査費用など総合的に判断して設定する必要があり、試行錯誤して見直しながら運用していくことも検討した方が良いかもしれません。
サンプルサイズ$n$と合格判定係数$k$を決める
$p_{0}$と$p_{1}$を設定したら、次はJIS規格の付表を元にサンプルサイズ$n$と合格判定値を決めます。
合格判定値の計算式は後述しますが、合格判定係数$k$を求めればあとは簡単な計算式で求めることができます。
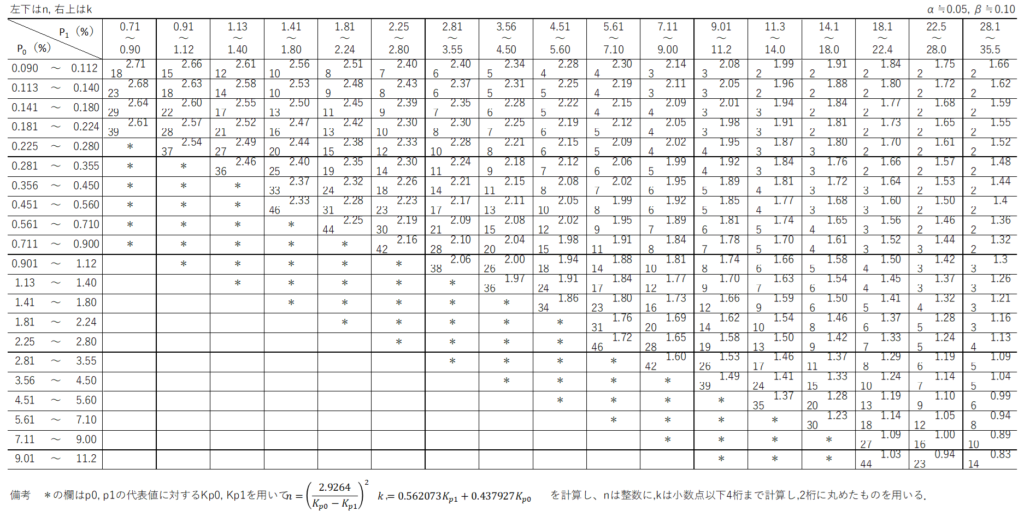
標準偏差が既知の場合はJIS Z 9003-1979の付表を用います。
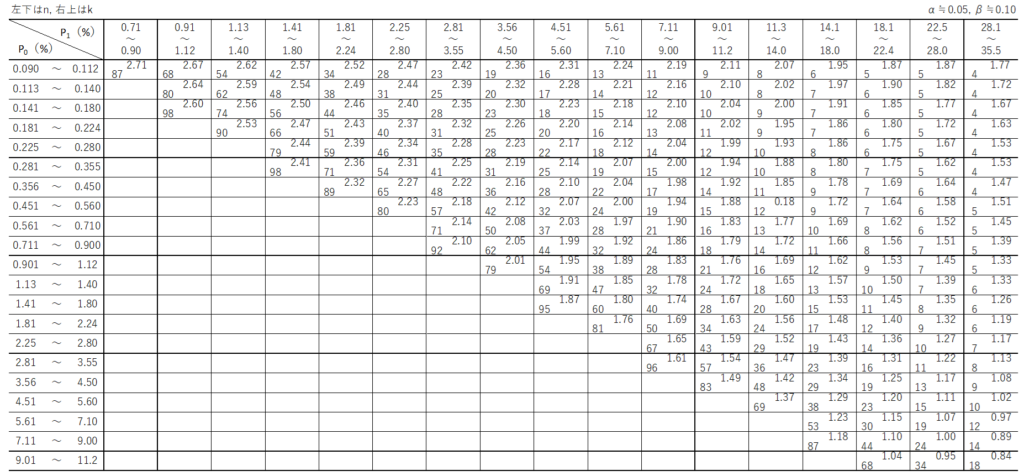
一方、標準偏差が未知の場合はJIS Z 9004-1983の付表を用います。
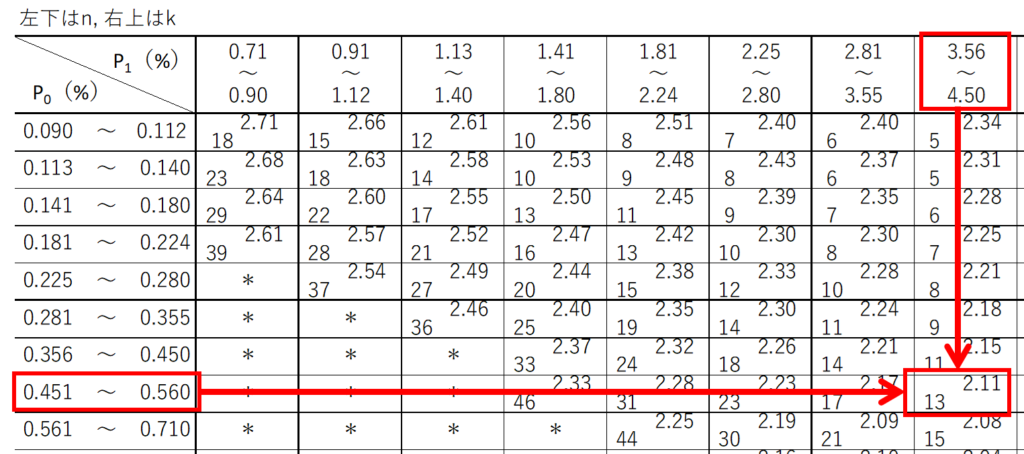
読み取り方は簡単で、設定した$p_{0}$と$p_{1}$に対応するセルの値を読み取るだけです。
例えば、$σ$既知で$p_{0}=0.5$%, $p_{1}=4.0$%の場合、$n=13$, $k=2.11$と読み取ることができます。
上限合格判定値$\bar{X}_{u}$は次の式から計算できます。
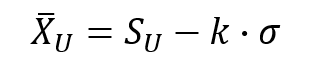
参考までに$k$の定義式の導出方法を記載します。

$α=0.05, β=0.10$の場合、$K_{α}=1.645, K_{β}=1.282$と決まるので、あとは$K_{p0}$と$K_{p1}$を標準正規分布表から読み取れば$k$の値は自力でも計算できます。
JISの付表では、$p_{0}$と$p_{1}$に対応する係数$k$の値があらかじめ記載されたもので、上記の計算を省略できる便利なものです。
ただ、多少の近似を含めている都合上、付表と手計算とでは最小桁が微妙に合わないのでご承知おきください。
なお、$n$に関しても同じく自力でも計算できますが、$σ$と$μ$の値を入れる必要があるので、こちらは付表から読み取る方が楽ちんです。
ロットからサンプルを採取して特性値を計測する
特性値の結果から平均値$\bar{x}$を算出します。
標準偏差が未知の場合には、取得した特性値を元にさらに不偏分散$s$を計算します。
合格・不合格の判定を下す
ロットの平均値$\bar{x}$と$\bar{X}_{u}$を比較して、合否判定を下します。
以上で不適合品率を保証する抜取検査を設計できました。

付表を読み取るだけでなく一回は自分で計算してみよう
JISの付表を用いれば、$p_{0}$と$p_{1}$から$n$と$k$が求められるので、やること自体はとてもシンプルですが、理屈を把握しておかないと応用が全く利きません。
反対に、自分で抜取検査を設計できれば、$n$と$k$の設計だけでなく、規格値の妥当性も判断できるようになるので、一度は基本からやってみることをおススメします。
まとめ
- 計量規準型抜取検査
サンプルの計量値を取得し、平均値と標準偏差から合否を判定する検査
計数規準型と比べてサンプルサイズを減らせる利点がある - 平均値を保証する検査の設計と手順
①:平均値の指標$m_{0}$と$m_{1}$を設定する
②:サンプルサイズ$n$と合格判定値を決める
③:ロットからサンプルを採取して特性値を計測する
④:合格・不合格の判定を下す - 不適合品率を保証する検査の設計と手順
①:上限規格値$S_{U}$(または$S_{L}$)を設定する
②:不適合品率の指標$p_{0}$と$p_{1}$を設定する
③:サンプルサイズ$n$と合格判定係数$k$を決める
④:ロットからサンプルを採取して特性値を計測する
⑤:合格・不合格の判定を下す
最後までご覧いただきありがとうございました。
抜取検査のエッセンスが詰まった本はズバリこれ
QC検定2級対策として、計数規準型抜取検査、計量規準型抜取検査を効率よく学習したい方はこちら
QC検定1級対策として、選別型抜取検査、調整型抜取検査を効率よく学習したい方はこちら




コメント
大変わかりやすかったです。
ちなみに、不良率のところで出てくる不適合品率P0とP1という解釈について、
P0:合格を誤って不合格にする確率なのでAQLの確率と同義
P1:不合格を誤って合格にする確率なのでLQの確率と同義
という理解であっていますか?
製造業で働く者ですが、抜取の設計に携わっており、AQLとLQの考え方と結びつけたいです
当サイトをご活用いただきまして、ありがとうございます。
P0とP1の解釈は、ご理解の通りです。
ありがとうございます!
返信いただけてうれしいです!
中心極限定理とか標準化とか使って読み解けるんだなと理解しました!