「定義の式の記号が多くて良く分からない」
「とにかく例題で設計のしかたのイメージを掴みたい」
「計算や表の読み取り方も順を追って全部教えてほしい」
このような疑問や悩みをお持ちの方に向けた記事です。
この記事では、計量規準型抜取検査の中でも、標準偏差が既知の場合においてロットの不適合品率を保証する検査に関する例題を紹介しています。
参考書などで定義は何となく理解したけれども、実際の使い方が良く分からず行き詰っているかたにとって、順を追って例題の解き方を説明するので参考になればうれしいです。
計量規準型抜取検査の種類や設計の基本的な考え方について、あらためてチェックしておきたい方には、以下の記事で詳しく解説していますので、合わせてご覧ください。

計量規準型抜取検査とは
最初に計量規準型抜取検査の基本的な項目について確認しておきましょう。
計量規準型抜取検査とは、正規分布を仮定できる製品において、とあるロットから抜き取ったサンプルの計量値を取得し、平均値と標準偏差から合否を判定する検査です。
「計量」とは量ることが可能な重さや寸法などの項目を意味し、不適合品数で判定する計数規準型抜取検査と比べて、サンプルサイズを減らすことができるメリットがあります。
主な種類としては、ロットの平均値を保証する方式と、ロットの不適合品率を保証する方式に分かれます。
後者の場合、生産者危険と消費者危険、規格値と判定値など、多くの記号が登場して少し複雑ですが、不適合品率を指標にすることから、汎用的で第三者へ説明しやすい利点もあります。
以降では、ロットの不適合品率を保証する検査において、平均値の低い方が好ましい場合と高い方が好ましい場合に分けて、例題を用いて設計のしかたと解き方を解説していきます。

数式と記号だけじゃ難しいから、図と一緒に理解していこう
例題1(平均値の低い方が好ましい場合)
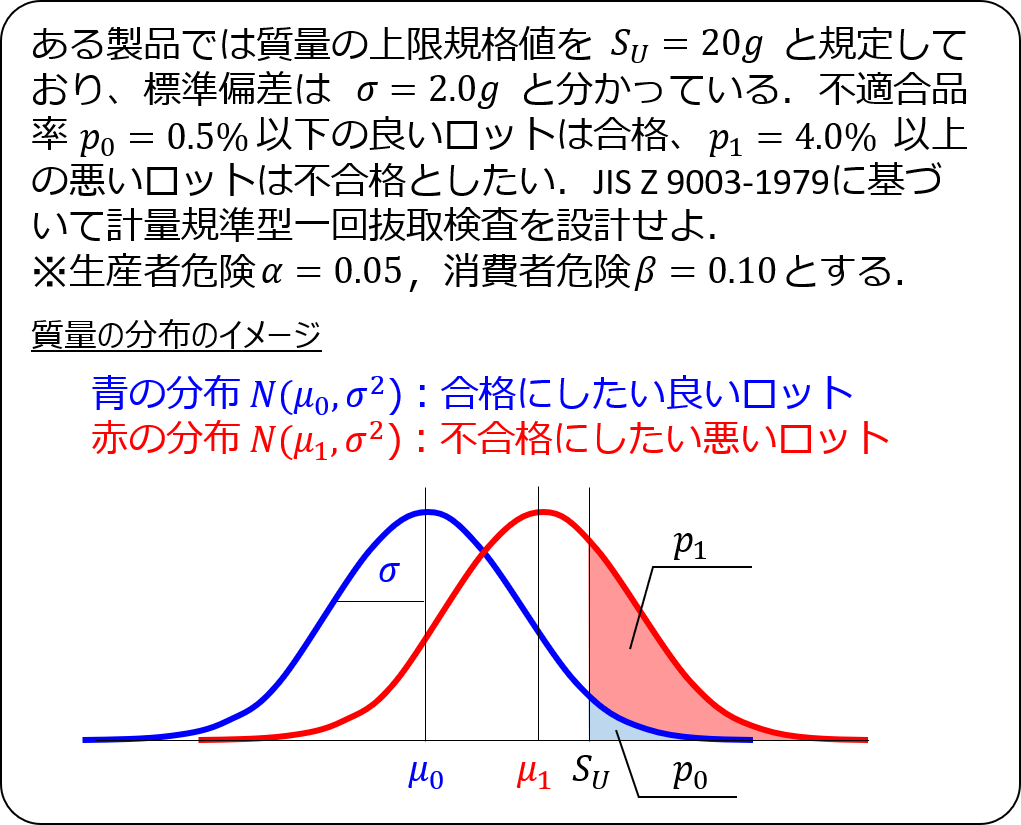
手順①:上限規格値$S_{U}$を設定する
まず抜取検査の前提となる上下限の規格値を設定します。
あらかじめ製品の規格が決まっていて明確な場合は、その値を適用します。
今回の場合は、問題文に与えられた値として、$S_{U}=20$とします。
規格自体がまだ明確ではなくて、抜取検査を設計した結果から妥当な値に見直したい場合でも、ここでは仮の値として$S_{U}$を設定して以降の計算を進めます。
手順②:不適合品率の指標$p_{0}$と$p_{1}$を設定する
保証したい不適合品率の指標を設定します。
平たく言うと、不適合品率が何パーセント以下であれば合格にしたいか、あるいは何パーセント以上なら不合格にしたいか、という意味合いです。
初心者の方にとっては、$p_{0}$と$p_{1}$を一体いくつに設定するのが妥当なのか感触が分からないという悩みもあると思いますが、心配する必要はありません。
一回で最適値を決める必要はなく、$S_{U}$と同様にひとまず仮の値として以降の計算を進め、例えばサンプルサイズが膨大になる場合には$p_{0}$と$p_{1}$の値を見直すなど試行錯誤して決めるのが通常です。
ちなみに、ざっくり言うと、$p_{0}$と$p_{1}$の値を近づけると合否判定が難しい検査になるので、必要なサンプルが多くなり、反対に遠ざけると緩い検査としてサンプルが少なくてすみます。
不適合品率の指標の設定が抜取検査の設計のすべてと言っても過言ではないので、検査の費用や精度など総合的に考慮して適切な値を決めるようにしましょう。
手順③:$μ_{0}$と$μ_{1}$を求める
手順①と②で前提を決めたら、あとは定義の式にもとづいて機械的に計算するのみです。
$μ_{0}$と$μ_{1}$を求めるには、品質特性$x$(今回の例題では質量)の分布を正規化して、$p_{0}$と$p_{1}$を標準正規分布の$K_{p}$値に変換すれば良いのです。
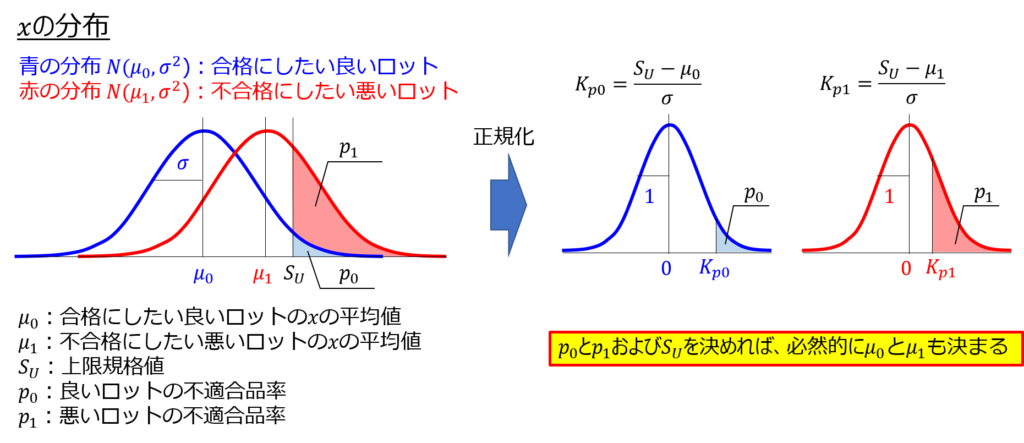
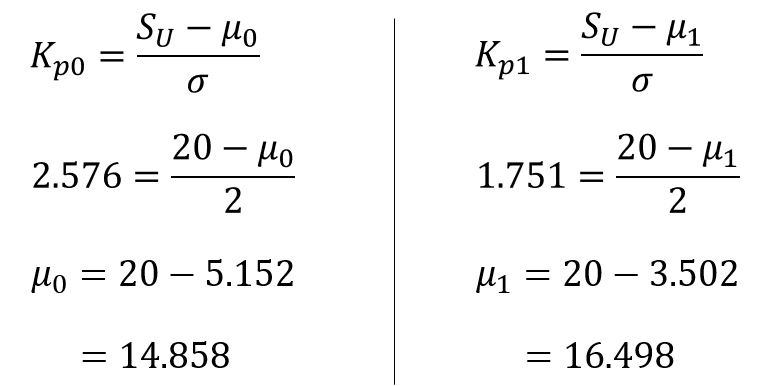
手順④:サンプルサイズ$n$と合格判定係数$k$を決める
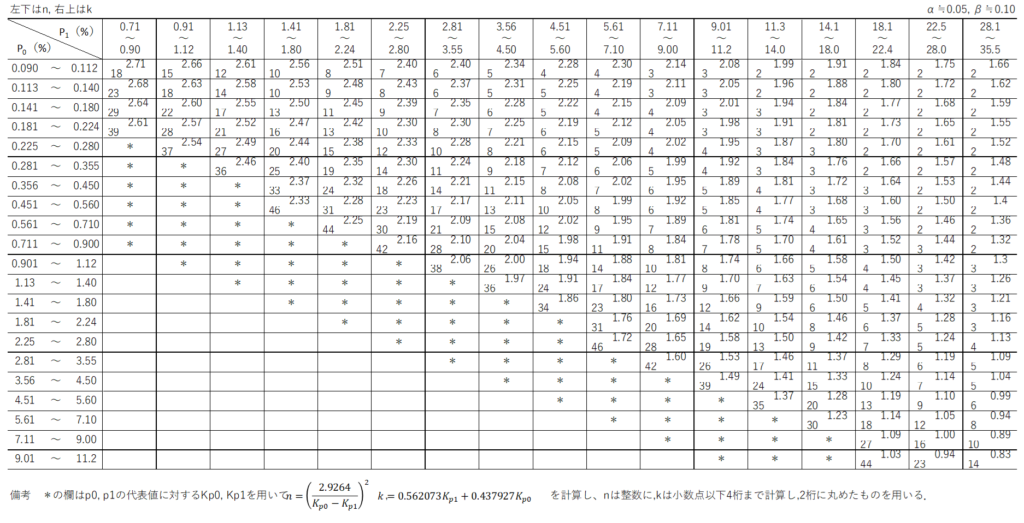
JISの付表を用いて、$p_{0}$と$p_{1}$に対応する$n$と$k$の値を求めます。
行と列に$p_{0}$と$p_{1}$の値が割り振られているので、該当する箇所の交差する値を読み取ります。
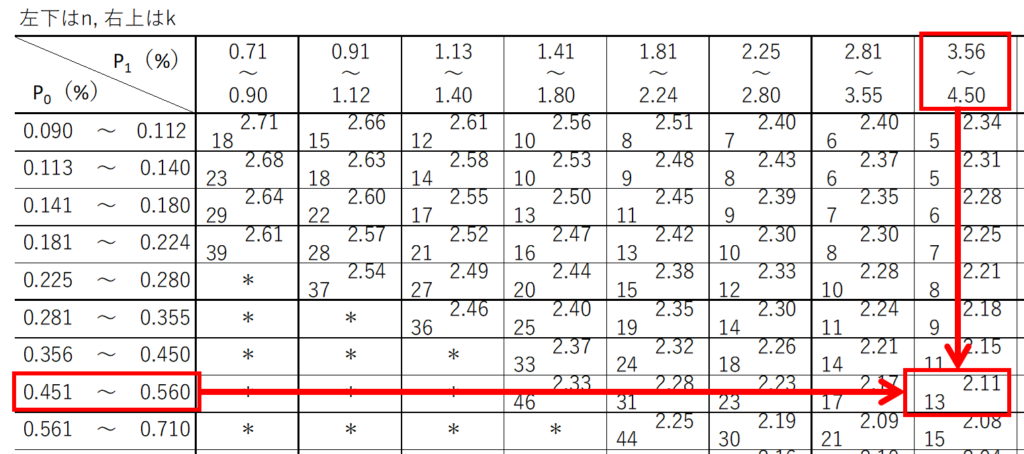
今回の場合、サンプルサイズ$n=13$、合格判定係数$k=2.11$となります。
手順⑤:上限合格判定値$\bar{X}_{U}$を求める
ロットから$n$個のサンプルを抜き取った平均値で合否判定をする場合、品質特性$x$の分布ではなく、品質特性の平均値$\bar{x}$の分布で考える必要があります。
正規分布$N(μ_{0}, σ^{2})$を仮定できるロットから$n$個のサンプルを抜き取って平均値を求めた場合、$\bar{x}$の分布は次のように$N(μ_{0}, σ^{2}/n)$の正規分布に従います。
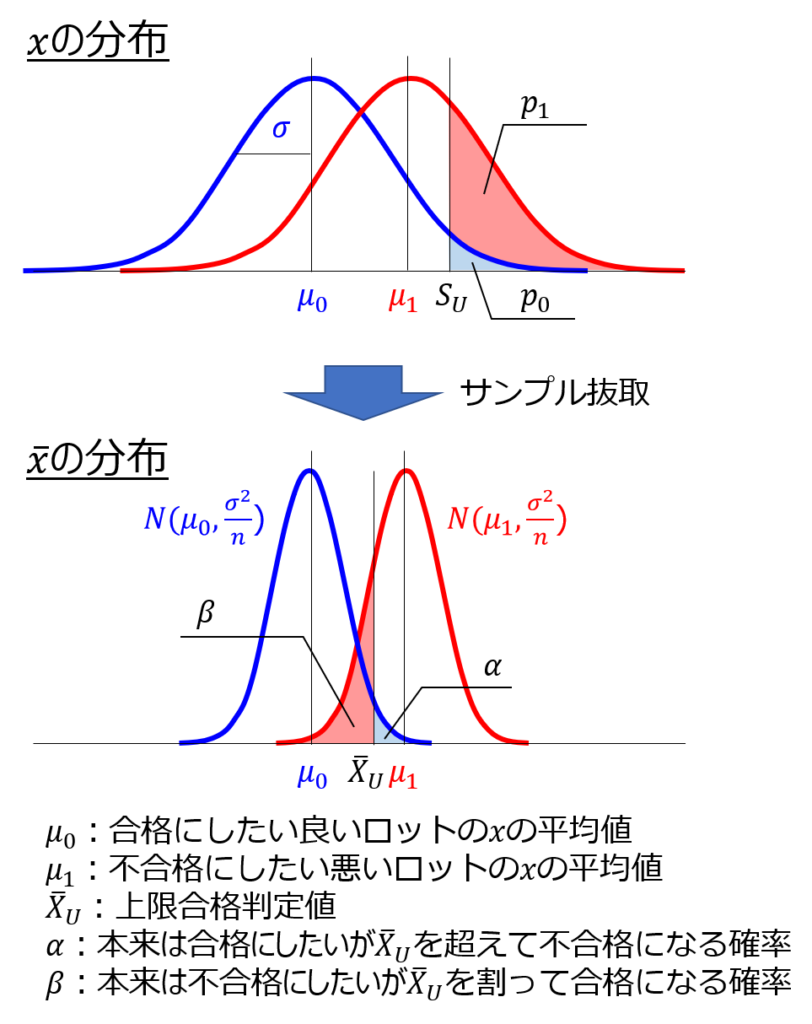
そして、先ほどと同様に標準正規分布の$K_{p}$値で議論できるよう、正規化を行います。
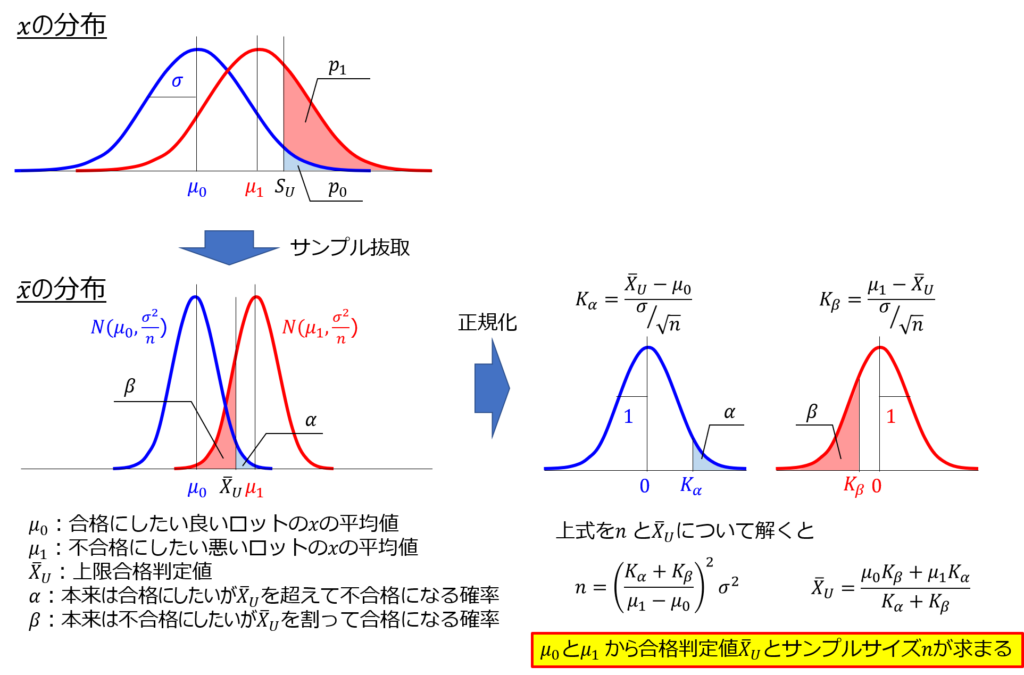
すると、$μ_{0}$と$μ_{1}$、$K_{α}$と$K_{β}$の値から$n$および$\bar{X}_{U}$が求められます。
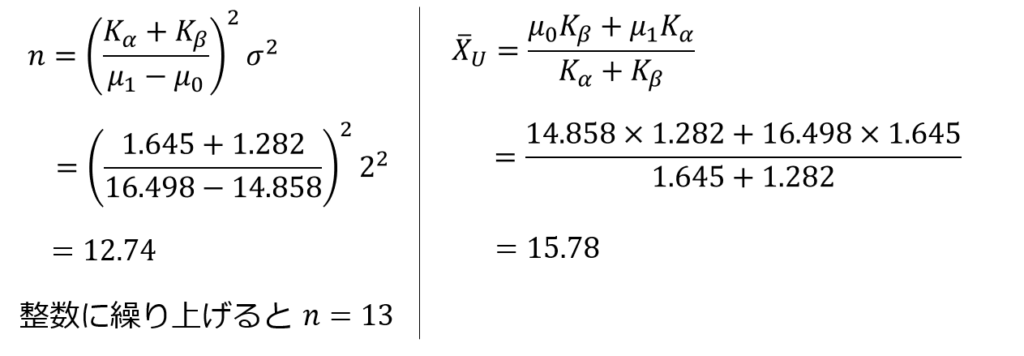
なお、ここで求めた$n$は先ほどのJISの付表から求めた結果と同じです。
また、$\bar{X}_{U}$についても合格判定係数$k$を用いて以下の式で求めることもできます。
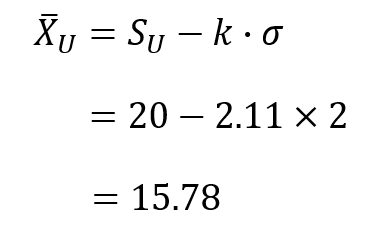
つまり、JISの付表はここで説明した正規化の手順を踏んで得られる計算結果を瞬時に求められる優れものなんです。

kを使えばこんな簡単な式でいいんだね
手順⑥:ロットの合格・不合格の判定を下す
合格判定値が決まれば、あとは実際にサンプルを採取して平均値$\bar{x}$が$\bar{X}_{U}$より小さければ合格、大きければ不合格と判定を下します。
大小の判定だけなので、判断基準が明確で分かりやすいですね。
例題2(平均値の高い方が好ましい場合)
平均値の低い方が好ましい場合と比べて、$μ_{0}$と$μ_{1}$の大小関係が反転するところだけ注意すれば考え方はほぼ同じです。
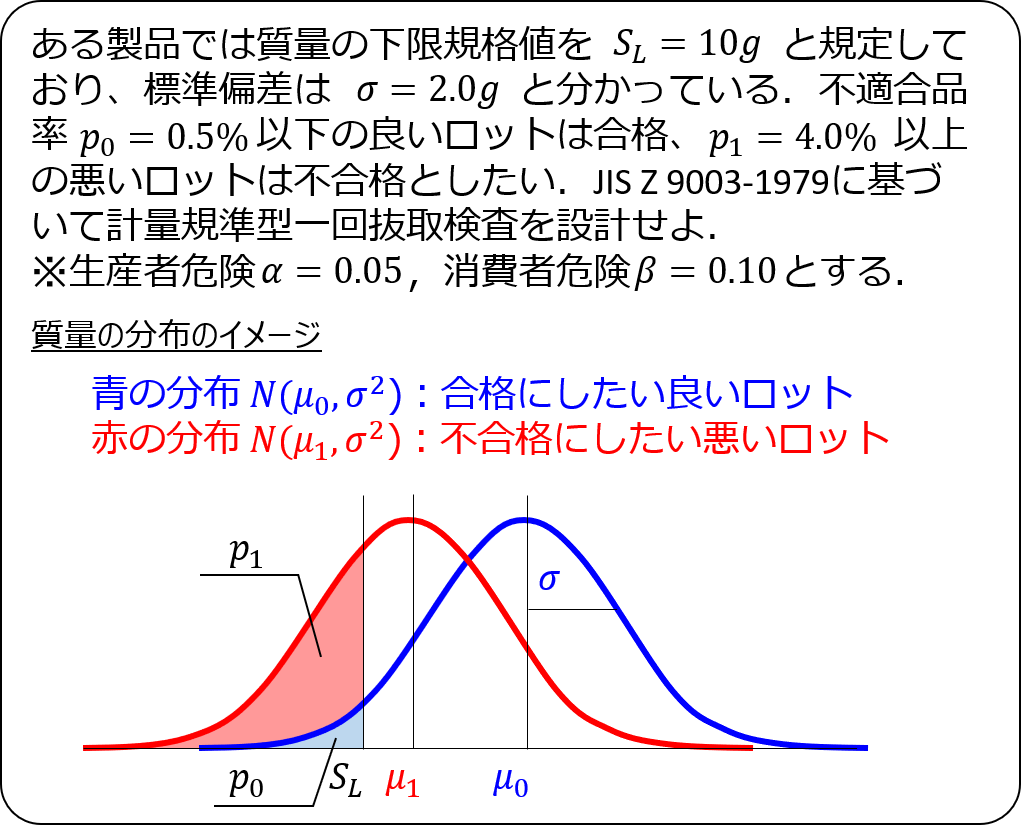
手順①:下限規格値$S_{L}$を設定する
今回の例題では、$S_{L}=10$となります。
手順②:不適合品率の指標$p_{0}$と$p_{1}$を設定する
不適合品率の指標は先ほどと同様、$p_{0}=0.5$%、$p_{1}=4.0$%とします。
手順③:$μ_{0}$と$μ_{1}$を求める
品質特性$x$の分布を正規化すると次のようになります。
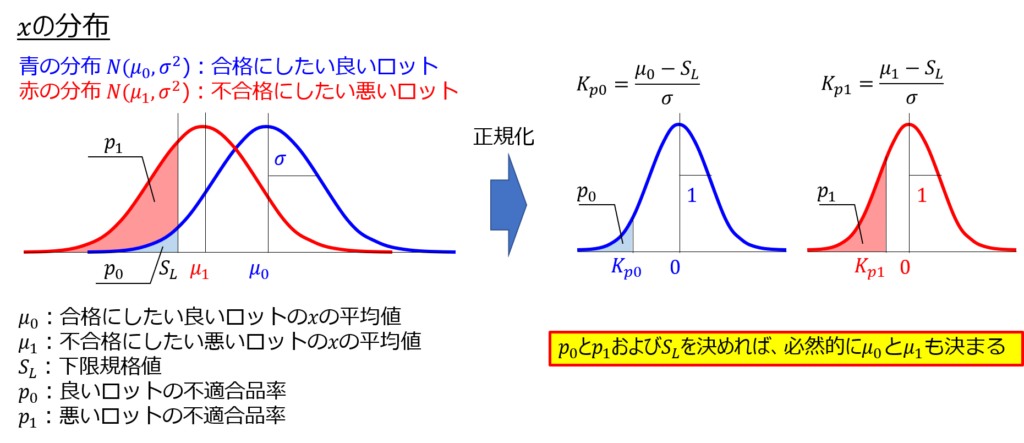
あとは、$μ_{0}$と$μ_{1}$について解けばそれぞれの平均値を求められます。
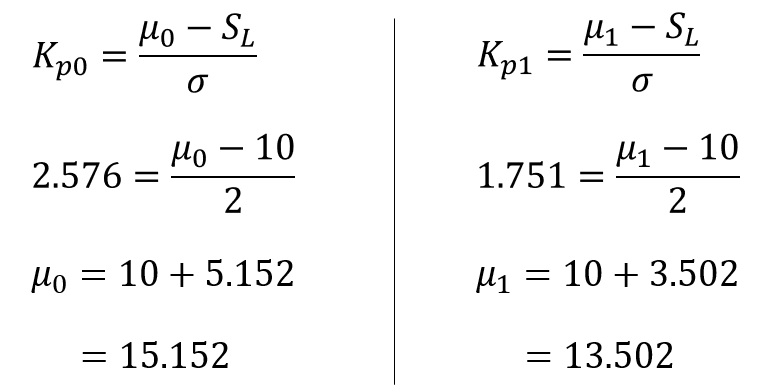
手順④:サンプルサイズ$n$と合格判定係数$k$を決める
サンプルサイズと合格判定係数については、$p_{0}$と$p_{1}$から求まるので、平均値が高いか低いか、どちらが好ましいかに関わらず決まってきます。
先ほどと同様にJISの付表から求めると、サンプルサイズ$n=13$、合格判定係数$k=2.11$となります。
手順⑤:下限合格判定値$\bar{X}_{L}$を求める
品質特性の平均値の分布を表すと次のようになります。
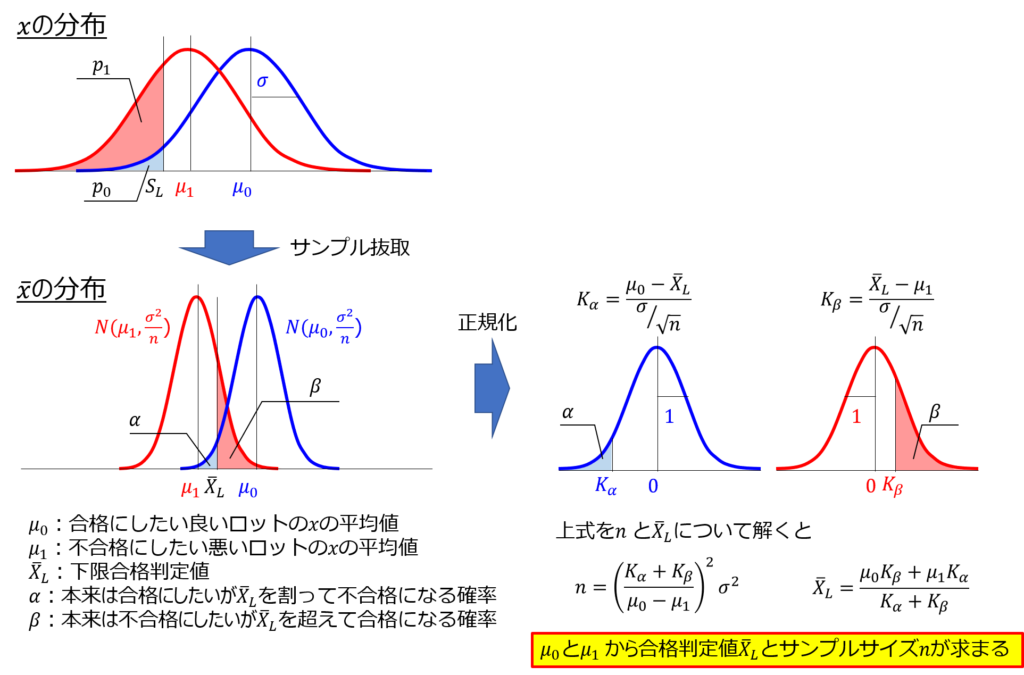
これを解くと、下限合格判定値$\bar{X}_{L}$を求められます。
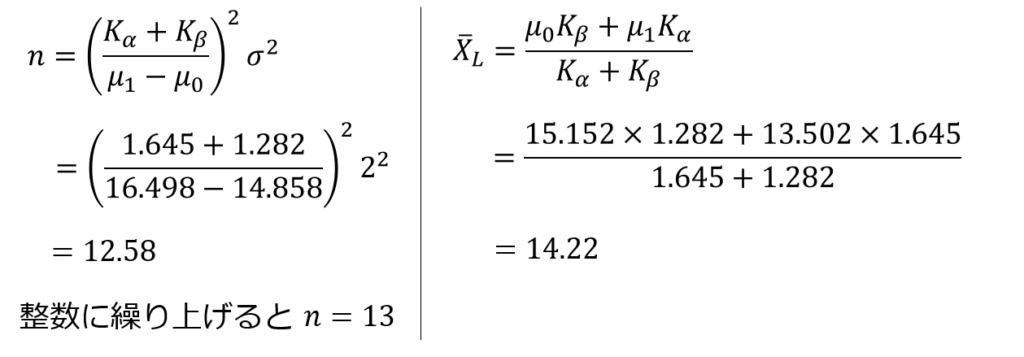
なお、合格判定係数$k$を用いると以下のように求めることもできます。
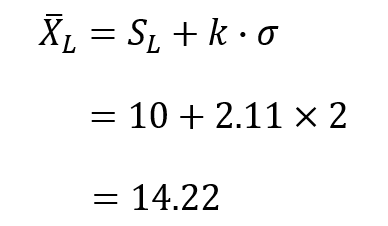
手順⑥:ロットの合格・不合格の判定を下す
合格判定値が決まれば、あとは実際にサンプルを採取して平均値$\bar{x}$が$\bar{X}_{L}$より大きければ合格、小さければ不合格と判定を下します。

あとは試行錯誤して適切な不適合品率を設定しよう
最後までご覧いただきありがとうございました。
抜取検査のエッセンスが詰まった本はズバリこれ
QC検定2級対策として、計数規準型抜取検査、計量規準型抜取検査を効率よく学習したい方はこちら
QC検定1級対策として、選別型抜取検査、調整型抜取検査を効率よく学習したい方はこちら




コメント