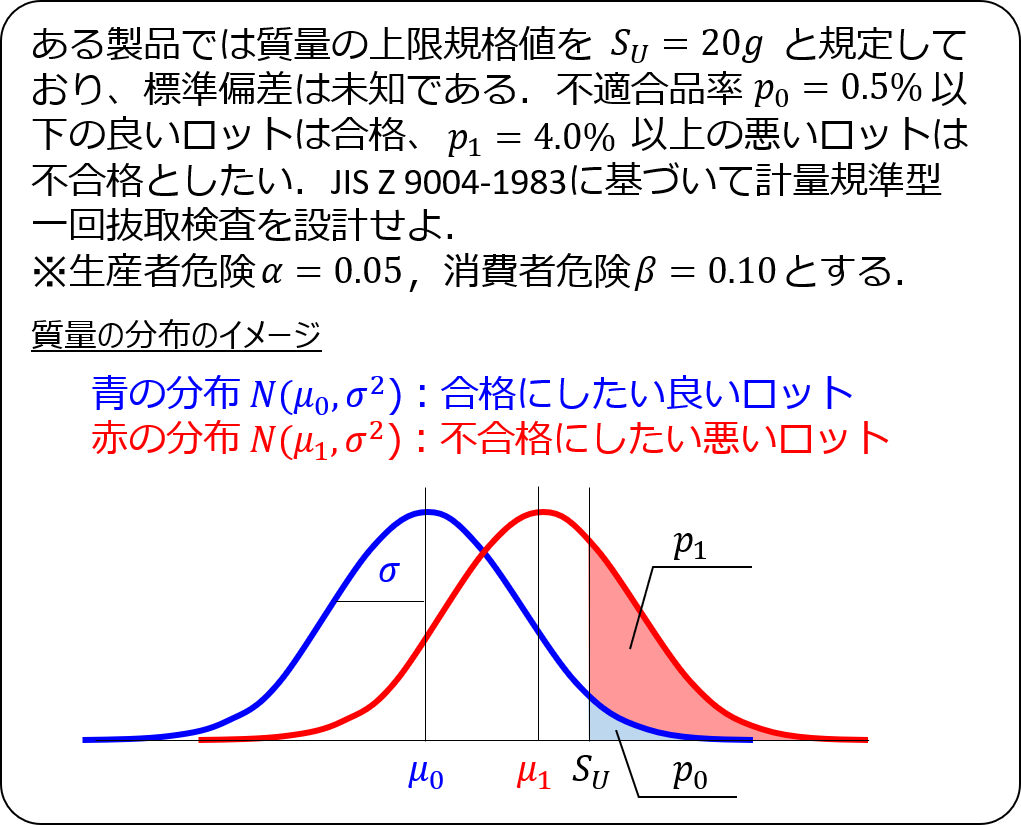
この記事では、計量規準型抜取検査の中でも、標準偏差が未知の場合においてロットの不適合品率を保証する検査に関する例題を紹介しています。
抜取検査の設計の手順としては、標準偏差が既知の場合と未知の場合で大した違いはありません。
ひとつ異なる点としては、未知の場合には抜き取ったサンプルから不偏分散を求める必要があるので、計算の順序が少し変わってくることです。
なお、計量規準型抜取検査の種類や設計の基本的な考え方を知りたいかたは、以下の記事で詳しく解説していますので、ご覧ください。


例題
手順①:上限規格値$S_{U}$を設定する
まず抜取検査の前提となる規格値を設定します。
あらかじめ製品の規格が決まっていて明確な場合は、その値を適用します。
今回の場合は、問題文に与えられた値として、$S_{U}=20$とします。
手順②:不適合品率の指標$p_{0}$と$p_{1}$を設定する
保証したい不適合品率の指標を設定します。
平たく言うと、不適合品率が何パーセント以下であれば合格にしたいか、あるいは何パーセント以上なら不合格にしたいか、という意味合いです。
これも問題文であらかじめ定義していますので、$p_{0}=0.5$、$p_{1}=4.0$と設定します。
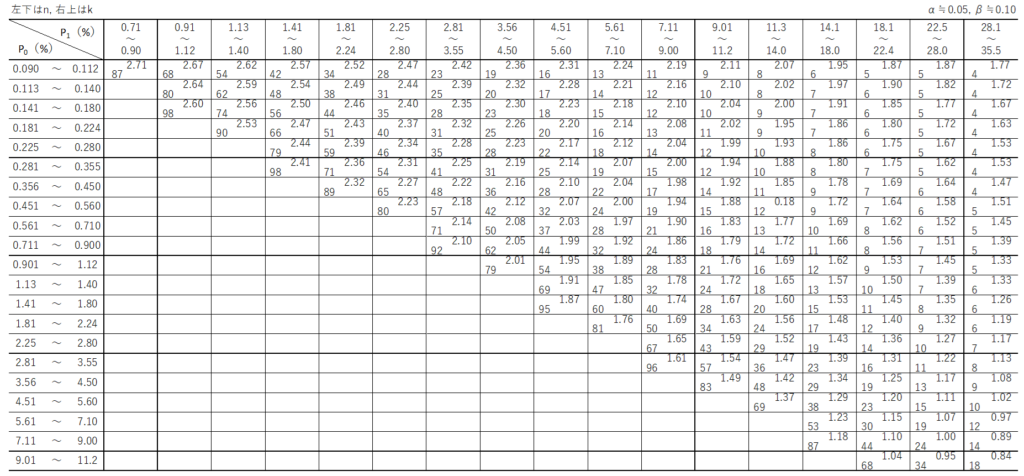
手順③:サンプルサイズ$n$と合格判定係数$k$を決める
JISの付表を用いて、$p_{0}$と$p_{1}$に対応する$n$と$k$の値を求めます。
この付表が、標準偏差が既知の場合と未知の場合で異なるので、取り違えないよう注意が必要です。
標準偏差が未知の場合、抜き取ったサンプルから不偏分散を求める必要があるので、既知の場合と比べて抜き取り数が多くなります。
行と列に$p_{0}$と$p_{1}$の値が割り振られているので、該当する箇所の交差する値を読み取ります。
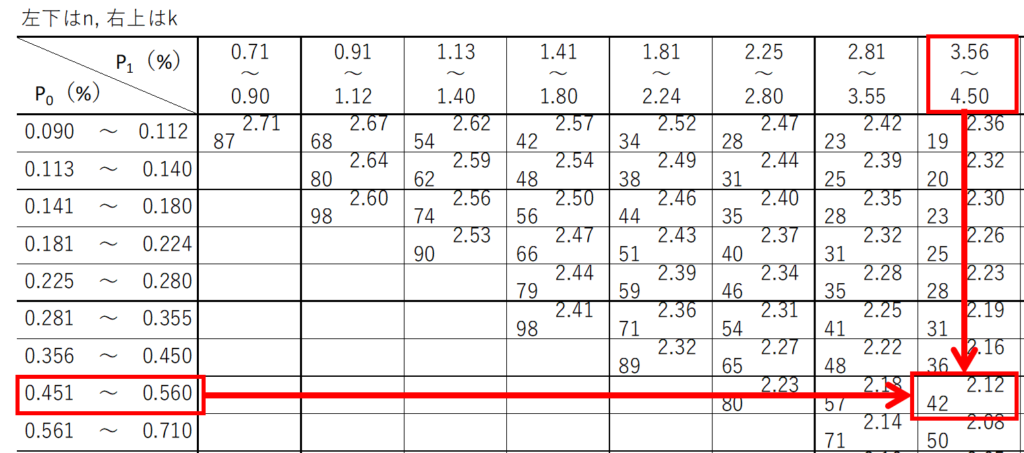
今回の場合、サンプルサイズ$n=42$、合格判定係数$k=2.12$となります。
なお、標準偏差が既知の場合では、$n$と$k$を求める前に$S_{U}$と$σ$の値から$μ_{0}$と$μ_{1}$を求めましたが、未知の場合では抜取検査を行ってからでないと不偏分散$s$が分かりません。
逆に言うと、既知の場合には必要な情報が最初から揃っているので、計算順序の制約が特にないということです。
未知の場合には採取したサンプルから不偏分散を求める必要があるので、そのために必要な$n$と$k$を最初に決めておくのです。
手順④:採取したサンプルから不偏分散を求める
先ほどのサンプルサイズ$n$に従い、サンプルを採取して計量値のデータを取得します。
得られたデータから不偏分散$s$を求めます。
今回の例題ではサンプルの生データと計算は割愛しますが、例えば不偏分散$s=3.0$とします。
手順⑤:上限合格判定値$\bar{X}_{U}$を求める
上限規格値$S_{U}$、合格判定係数$k$、不偏分散$s$の値から$\bar{X}_{U}$を求めます。
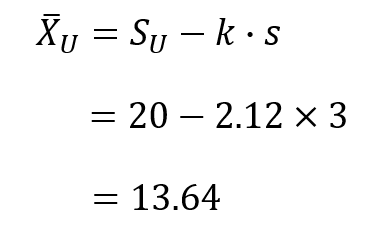
手順⑥:ロットの合格・不合格の判定を下す
合格判定値が決まれば、あとは実際にサンプルを採取して平均値$\bar{x}$が$\bar{X}_{U}$より小さければ合格、大きければ不合格と判定を下します。
最後までご覧いただきありがとうございました。
抜取検査のエッセンスが詰まった本はズバリこれ
QC検定2級対策として、計数規準型抜取検査、計量規準型抜取検査を効率よく学習したい方はこちら
QC検定1級対策として、選別型抜取検査、調整型抜取検査を効率よく学習したい方はこちら




コメント