この記事では、2つの母不適合数の差における統計的検定について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
なお、統計的検定の概念とメリット、登場する用語の意味など、統計的検定(その1)の記事から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

また、この記事では、母不適合数の定義やポアソン分布との関係性についての基本的な説明を省略しています。
あらためて定義から確認したいという方は、合わせて参考にしていただければ幸いです。


2つの母不適合数の差の検定
検定統計量
2つの母不適合数の差の確率分布に関しても、1つの母不適合数と同様に、標準正規分布$N(0,1)$に従います。
標準正規分布では、分布の横軸($Z$値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのNORM.S.DIST関数や標準正規分布表で簡単に求められます。
2つの集団を$A, B$と名付けると、母不適合数の差の検定統計量は以下のように表されます。
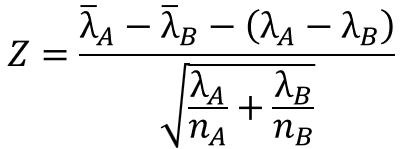
$A$と$B$はそれぞれの集団を意味し、$\bar{λ}_{A}$, $\bar{λ}_{B}$は標本不適合数、$λ_{A}$, $λ_{B}$は母不適合数、$n_{A}$, $n_{B}$はサンプルサイズを表します。
計算式の構造は、1つの母不適合数の場合と同じなので覚えやすいですね。


その1から勉強してきた人は見慣れた形だよね
そして、統計的検定では帰無仮説として母不適合数に差がないことを仮定するので、$λ=λ_{A}=λ_{B}$と置くと、先ほどの式は以下のように変換されます。
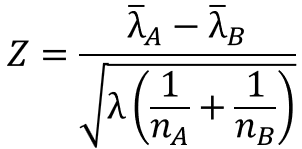
ここで、$λ$は$A$と$B$を合わせた平均不適合数として、以下のように標本データから推定量を定義します。
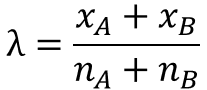
$λ$が単位時間あたりの不適合数で定義されることに対し、$x_{A}$, $x_{B}$は観測したトータルの不良数を意味します。
この式に標本データから得られた不適合数とサンプルサイズを代入することで、検定統計量を求めることができます。
検定の手順
それでは、実際に母不適合数の差の検定をやってみましょう。
とある製品をAラインとBラインの2つの生産ラインで製造しています。過去10年間の不具合発生数を集計した結果、Aラインは12回、Bラインは4回であったとき、1カ月当たりのラインAとBの母不適合数に差があると言えるでしょうか?
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
2つの母不適合数に違いがあることを背理法で証明したいので、帰無仮説を「$H_{0}:λ_{A}=λ_{B}$」、すなわち「2つのラインの不適合数に違いがない」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「2つのラインの不適合数に違いがある」とします。
$H_{0}:λ_{A}=λ_{B}$
$H_{1}:λ_{A}≠λ_{B}$(両側検定)
2.検定統計量を算出する
定義の数式に従い、検定統計量$Z$を求めます。

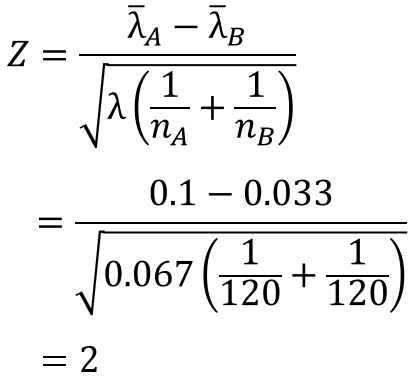
ここで注意が必要なのが、求めたいサンプルサイズに換算した単位当たりの不適合数を算出することです。
今回の場合、標本データのサンプルサイズは$n_{A}=n_{B}=120$(1カ月×120回)です。
3.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
判定の指標には、標準正規分布の$Z$値を用います。
通常、統計的検定では、有意水準$α=0.05$や$α=0.01$を基準として用います。
つまり、本当は帰無仮説が正しいのに、誤って棄却してしまう確率が$α=0.05$の場合は5%、$α=0.01$なら1%となる状態のことです。
エクセルで標準正規分布の累積分布関数の逆関数を表すNORM.S.INV関数を使えば、$α=0.05$における棄却域を以下のように求められます。
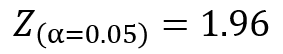
先ほどの検定統計量と比較すると、以下の関係であることが分かります。
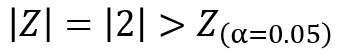
5%の棄却域に入っている状態、つまり有意水準5%で帰無仮説が棄却され、対立仮説が採択されるという結果となります。
4.検定の結論を導く
検定の結果から、今回の結論を出します。
「有意水準5%でラインAとBの不適合数に違いがあると言える」
まとめ
- 2つの母不適合数に関する検定統計量
⇒標準正規分布のZ値を用いる - 検定の手順
⇒仮説を設定する
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント