この記事では、分割表による独立性の検定について記載していますので、参考なればうれしいです。
独立性の検定は、この記事で完結して解説していますが、統計的検定の概念とメリット、登場する用語の意味など、その1から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

分割表とは?
まず、分割表という聞き慣れない言葉から不安を感じるかもしれませんが、百聞は一見に如かず、ということで具体例から示します。
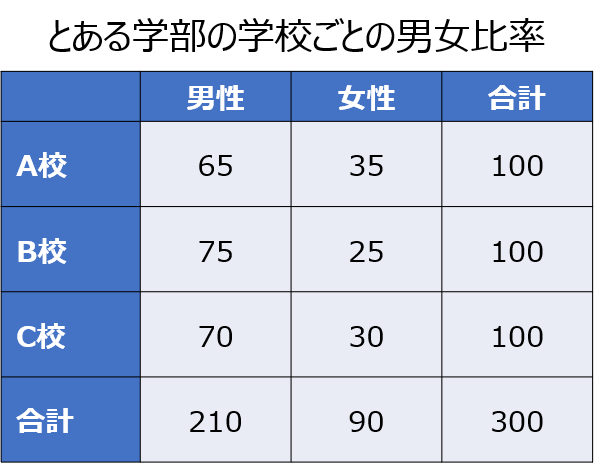
「なんだ、よく見かける二元表じゃないか」と感じた方も多いと思いますが、まさにその通りです。
行と列に変数の項目を取り、これらの交差する箇所に計数値の集計結果を記載したものを分割表(クロス集計表)と呼びます。
m行、n列の分割表のことを「m×n分割表」と表現し、先ほどの例では3×2分割表ということになります。
独立性の検定とは?
次に、独立性の検定について説明します。
分割表において、変数どうしの関連性がないことを「独立」と表現します。
例えば、先ほどの分割表で学校ごとの男女比率に違いがあるかどうか考えてみましょう。

分割表を見て、どの学校も男性比率の方が高いことは何となくわかると思います。
ただ、この微妙な違いが学校ごとの違いの影響があるのか、それとも学校によらずこの学部では共通的に男性比率が高いのか、数字を眺めているだけでは判断が付きません。
これを統計的に定量値で判断するための手段として統計的検定が用いられ、独立性の検定と呼ぶのです。
独立性の検定の手順
検定統計量
独立性の検定では、適合度検定と同じくカイ二乗分布の考え方を使います。
適合度検定の解説記事を既にご覧いただいた方は、「検定の手順」まで読み飛ばしていただいて構いませんが、あらためて軽くおさらいをしておきます。
「カイ」は記号で「$χ$」と表され、以下の数式によって定義されます。
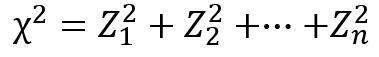
ここで、$Z_{1}~Z_{n}$は標準正規分布に従う互いに独立な確率変数を表します。
標準正規分布とは、正規分布において平均値$μ$を0、標準偏差$σ$を1として基準化したもので、$N(μ,σ^{2})$は$N(0,1)$と表記されます。
この$χ^{2}$が従う確率分布のことをカイ二乗分布と呼び、自由度$n-1$のカイ二乗分布に従うと表現されるのです。
確率変数の二乗和が従う分布なので、すなわち、「ばらつき」「分散」に関わる確率を求める場合に活用され、まさに適合度検定や独立性の検定の目的に合致した手法なのです。
以下の記事も合わせてご覧ください。



検定の手順
先ほどの分割表を用いて、実際に独立性の検定をやってみましょう。

1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
学校ごとの男女比率に違いがあることを背理法で証明したいので、帰無仮説を「$H_{0}$:学校ごとの男女比率に違いはない」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「男女比率に違いがある」とします。
$H_{0}$:男女比率に違いはない(行と列は独立である)
$H_{1}$:男女比率に違いがある(行と列は独立でない)
2.検定統計量を算出する
カイ二乗値の定義に従い、検定統計量を求めます。
まずは、学校ごとの影響がないものとして、男女比率の期待度数を出します。
考え方は単純で、A校からC校の違いをいったん無視して、合計値から理論比率を算出します。
今回の例では21:9となり、つまり100パーセント比率に直すと70:30が期待度数ということになります。
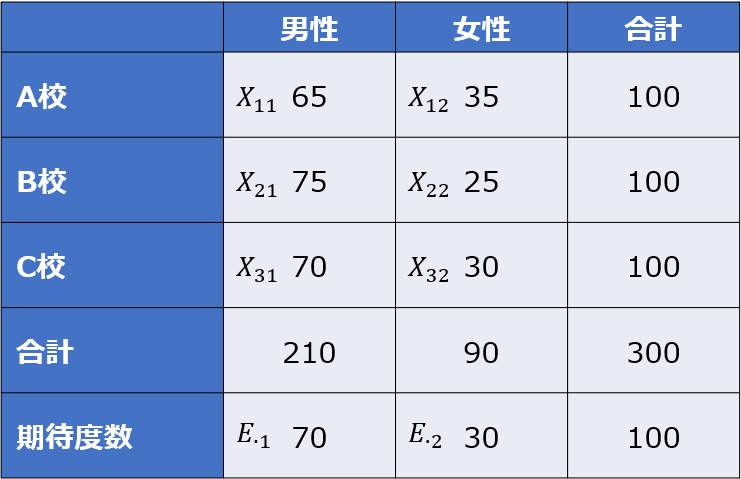
次に、A校からC校の実際の観測値と期待度数とのずれを求め、すべての表の欄のずれ量を合算すると、検定統計量であるカイ二乗値が計算できます。
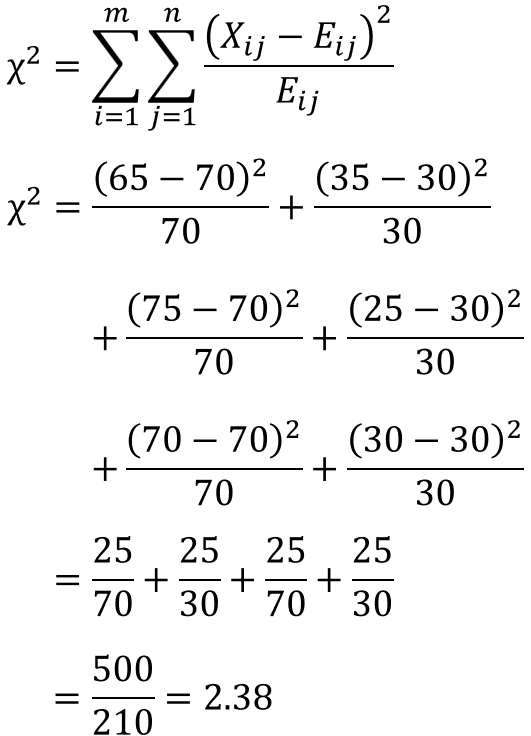
3.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
ここで用いる自由度は、$φ=(m-1)×(n-1)$で求められ、今回の場合は2となります。
判定のしかたは、母分散の検定と同じくカイ二乗表、またはエクセル関数(CHISQ.INV関数)を用いて閾値(しきい値)との大小関係を見ます。
これも適合度検定と同様に、片側検定で上側確率を判定の対象とします。
今回の場合、有意水準$α=0.05$における棄却判定値は次のように読み取ることができます。
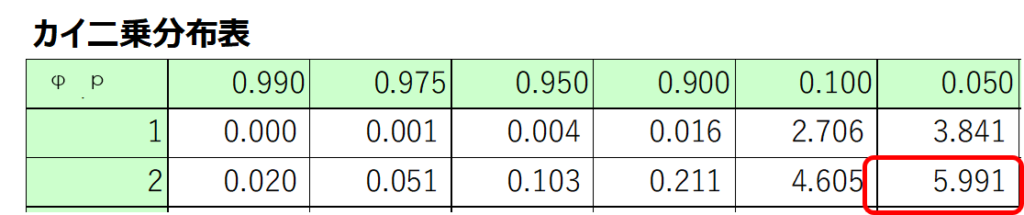

先ほどの検定統計量と比較すると、以下の関係であることが分かります。
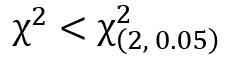
帰無仮説を棄却できず採択されます。
4.検定の結論を導く
検定の結果から、今回の結論を出します。
「学校ごとの男女比率に違いがあるとは言えない」
まとめ
- 分割表(クロス集計表)
⇒行と列に変数の項目を取り、これらの交差する箇所に計数値の集計結果を記載した表 - 独立性の検定
⇒分割表において、変数どうしの関連性がない(独立である)ことを検定統計量で定量的に調べる手法 - 検定の手順
⇒仮説を設定する
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント