この記事では、対応のある2つの正規分布における母平均の差の統計的検定について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
また、対応のある母平均の差の検定は、エクセルのアドインの分析ツールを用いて、簡単に検定統計量やP値を求めることができます。
分析ツールの使い方や計算式の内容についても解説しますので、参考になればうれしいです。
なお、統計的検定の概念とメリット、登場する用語の意味など、統計的検定(その1)の記事から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

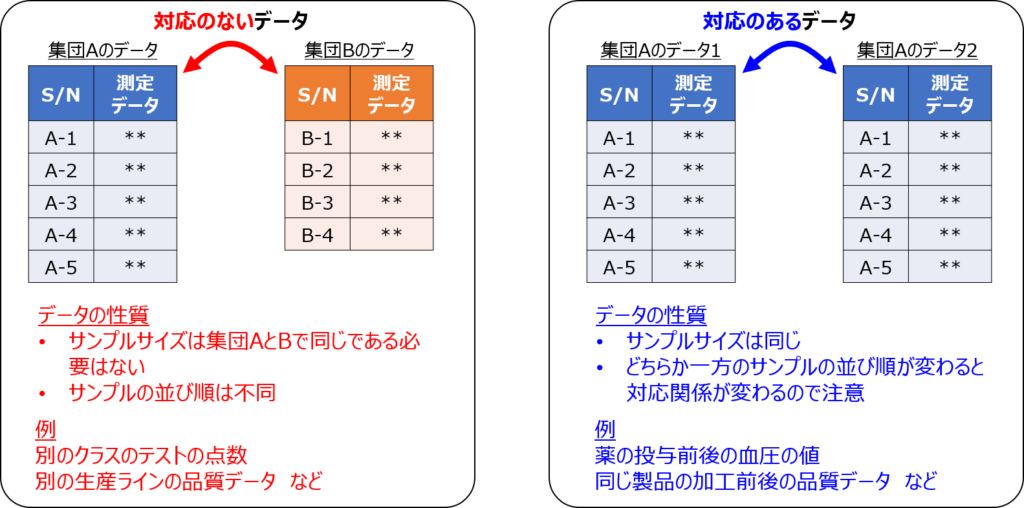
対応のあるデータとは?
2つの母集団のデータに関連がある場合で、例えば、とある病気の患者に薬を投与した際の効果を比較するケースなどに用いられる手法です。
そのため、2つのデータのサンプルサイズは同じであり、また、それぞれの対応関係が入れ替わらないようサンプリング番号の対応も決まっています。

順番がばらばらだと正しく差を取れないから気を付けよう
「対応のないデータ」と間違えやすいので、それぞれの特徴に注意しながら使いこなせるようにしておきましょう。
対応のある母平均の差の検定
検定統計量
対応のあるデータの母平均の差の確率分布は、対応のないデータの場合と同様にt分布に従います。
t分布とは以下の数式により求められる統計量t値が従う確率分布のことです。

$\bar{x}$は標本平均、$μ$は母平均、$s^{2}$は不偏分散、$n$は自由度を表します。
詳しくは別の記事で解説していますので、合わせてご覧ください。

t分布では、分布の横軸(値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのT.DIST関数やt分布表で簡単に求められます。
そして、この値を検定統計量として用いることで、母平均の差に対する検定を行うことができるのです。
検定統計量は、以下の数式で表されます。
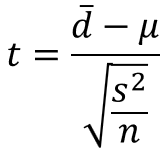
$\bar{d}$は対応するデータの差の平均値、$μ$は母平均の差、$s^{2}$はデータの差の不偏分散、$n$はサンプルサイズを表します。
対応のないデータの場合と異なるのは、それぞれのデータが一対になっているので、「データの差」をパラメータとした統計量を用いることです。
元のデータは2つの集団から構成されますが、最初にデータの差を取って平均値と不偏分散を計算すれば、あとは1つの母平均に関する検定と同じ考え方です。
平均値に関する検定は、その壱の記事で詳しく解説していますので、合わせてご覧ください。

検定の手順
それでは、実際に母平均の差の検定をやってみましょう。
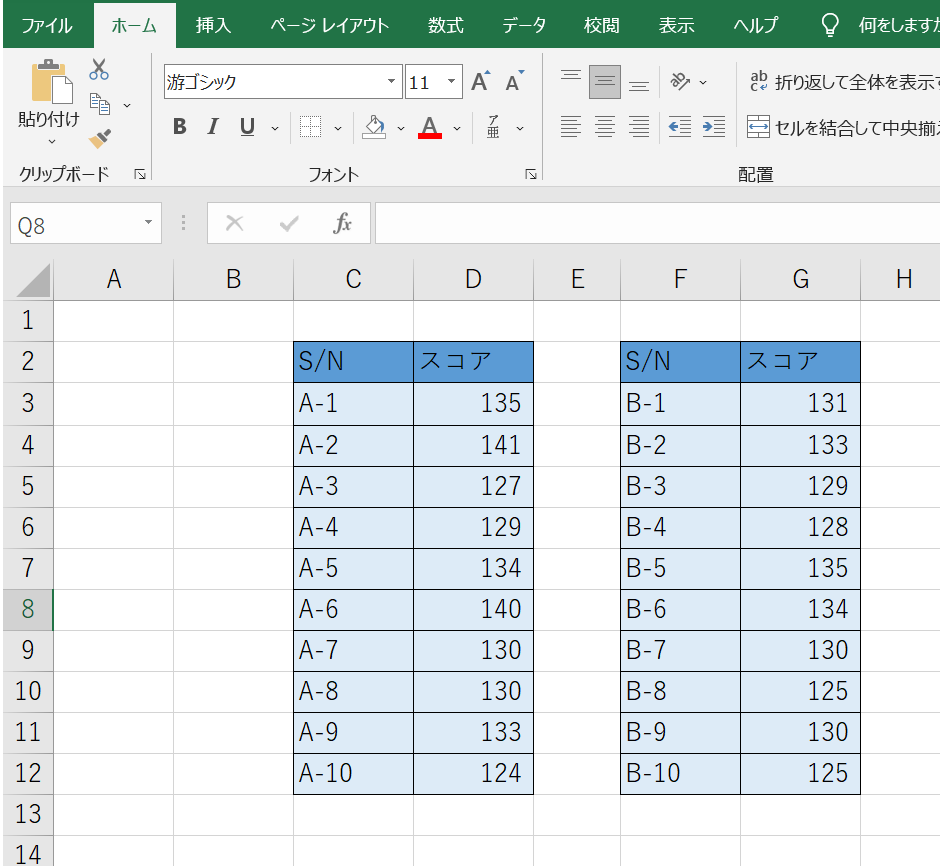
以下は、とある病気の患者に薬を投与したときの検査データの結果です。
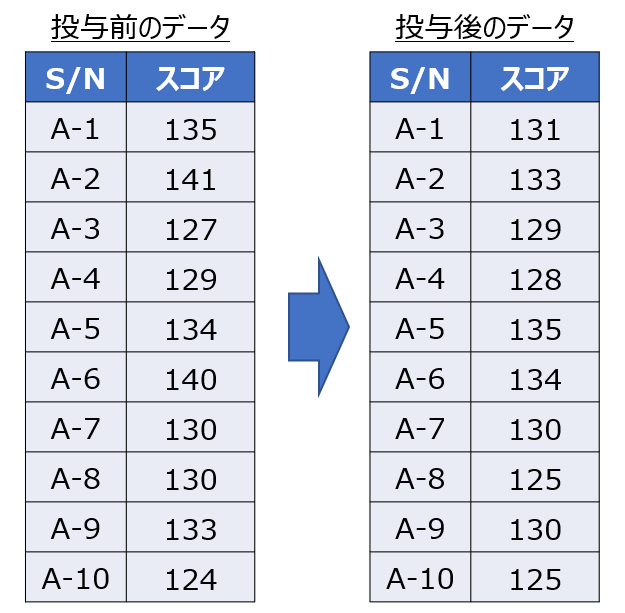
投与前後の分布がそれぞれ正規分布に従うとき、母平均に差があると言えるでしょうか?
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
投与前後の母平均に差があることを背理法で証明したいので、帰無仮説を「$H_{0}:μ=0$」、すなわち「投与前後の母平均に違いがない」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「投与前後の母平均の差は0とは言えない」とします。
$H_{0}:μ=0$
$H_{1}:μ≠0$(両側検定)
対立仮説を「$H_{1}:μ>0$(投与前の母平均の方が小さい)」と設定した場合には、片側検定となるので間違えないように注意しましょう。
2.データの差を求める
2つの集団の対応するデータの差を取ります。
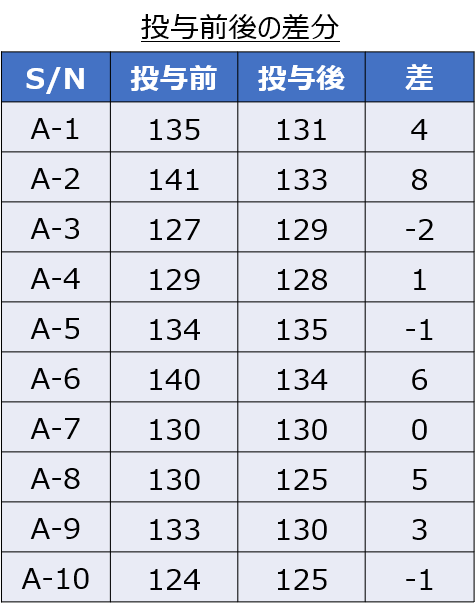
元データを使用するのはここまでで、以降では「データの差」をパラメータに扱います。
3.平均値と不偏分散を求める
先ほど求めたデータの差に対して平均値と不偏分散を求めます。
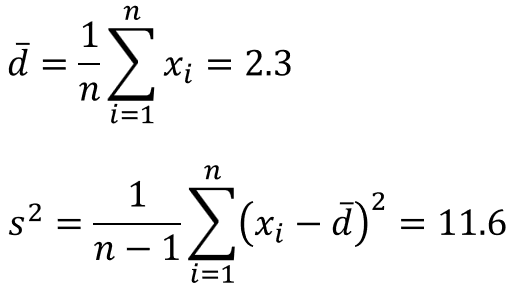
4.検定統計量を算出する
定義の数式に従い、検定統計量$t_{0}$を求めます。
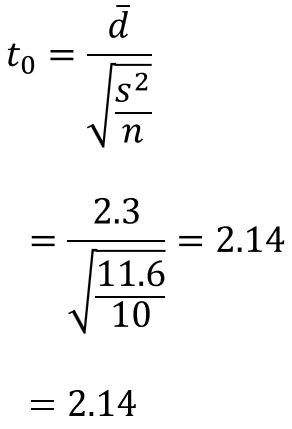
5.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
両側検定の場合、先ほど求めた検定統計量$t_{0}$と有意水準に対応するt値との間に、以下の関係が成り立つと帰無仮説が棄却されます。
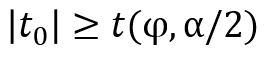
t分布表から自由度9と両側確率0.05におけるt値(2.262)を読み取ります。
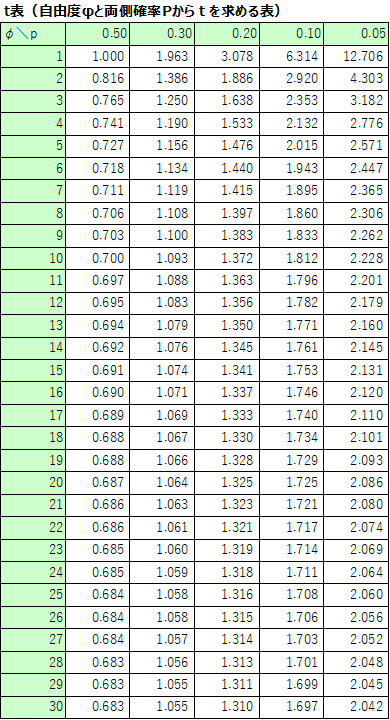
ここで注意が必要なのが、「対応のない母平均の差」とは異なり、自由度はデータの対になる数をサンプルサイズとした場合のことで、今回のケースでは$φ=10-1=9$となります。
ちなみに、エクセルのT.INV.2T関数やT.INV関数を用いてもt値を求めることができます。
T.INV.2T関数とは、t分布の両側確率の逆関数を表すもので、今回の場合、$=T.INV.2T(0.05,9)$と入力すると同じ値が得られます。
また、T.INV関数は下側(左側)確率の逆関数を表すもので、片側検定を行う場合に用いると有効です。
6.検定の結論を導く
検定統計量$t_{0}$の絶対値は、棄却限界値よりも小さく、帰無仮説を棄却することができません。
すなわち、「母平均に違いがあるとは言えない」となります。

両側検定は絶対値で判定するんだったね
エクセルを用いた検定
エクセルの分析ツールを使ってt検定を容易に行うことができます。
分析ツールのアドインの設定のしかた、P値の意味や結果の判定のしかたについては、前章で詳しく解説していますので、ぜひご覧ください。

分析ツールの使い方
まずはツールを起動する前に、検定に用いるデータをエクセルに入力します。
「データ」タブを選択し、「データ分析」をクリックして立ち上げます。

「t検定:一対の標本による平均の検定」を選択して「OK」を押します。
変数1と変数2の入力範囲に対応するデータを選択し、有意水準αを設定します。
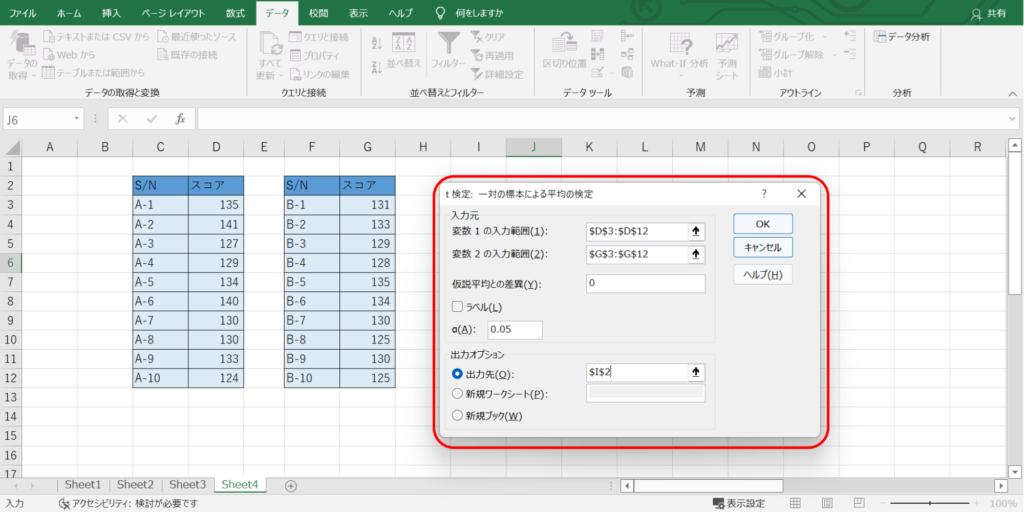
仮説平均との差異については、今回の場合、平均値に差がないことを示したいのでゼロとします。
結果を記載する出力先を設定して、「OK」を押します。
結果の見かたと計算式
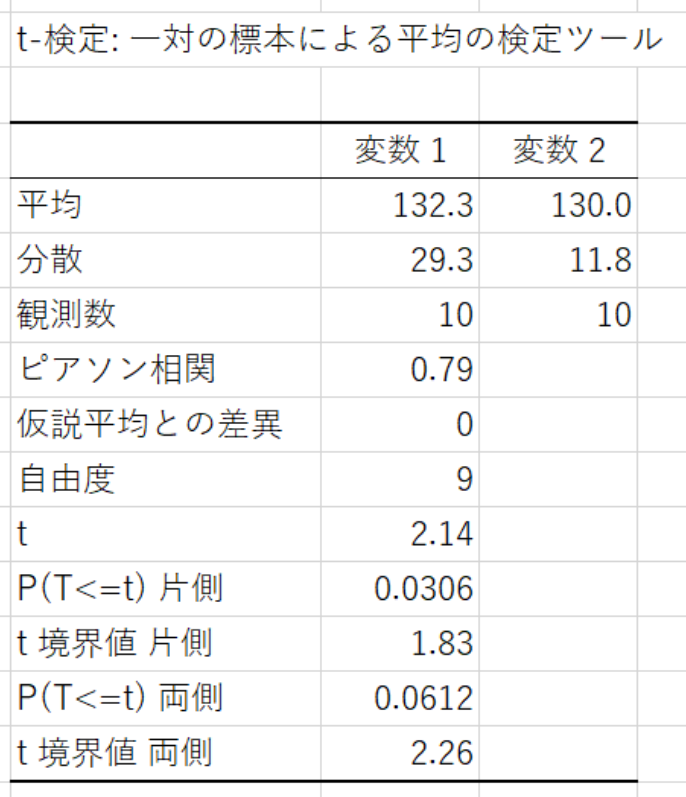
平均:標本データの平均値
分散:標本データの不偏分散
観測数:標本データのサンプルサイズ
ピアソン相関:標本どうしの相関係数
t:標本データから求めた検定統計量
t境界値片側:片側検定において有意水準αとなるt値
t境界値両側:両側検定において有意水準αとなるt値
得られたt値が先ほどの計算結果と合致することが分かりますね。
まとめ
- 対応のある母平均の差に関する検定統計量
⇒t分布のt値を用いる
サンプルサイズは同一、データの並び順に注意 - 検定の手順
⇒仮説を設定する
データの差を求める
平均値と不偏分散を求める
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント