「無相関の検定って何のためにやるの?」
「なぜ相関が無いことを検定するの?」
「検定のやり方について順を追って理解したい」
このような疑問や悩みをお持ちの方に向けた記事です。
相関とか検定とか、単独で登場しても厄介なのに、これらが組み合わさった「無相関の検定」なんて、名前を聞くだけで難しそうなイメージが付きますよね。
この記事では、無相関の検定の目的と考え方、検定統計量の導出のしかたについて、できるだけ難しい数式を使わず、例題を交えて解説しています。
ぜひ最後まで読んで参考にしていただければと思います。
また、YouTubeチャンネルでは、このブログの内容を動画で解説していますので、あわせてご覧いただけると幸いです。
無相関の検定とは?
無相関の検定(無相関検定とも言います)とは、相関係数に意味があるのか統計的に調べる手法のことです。
相関係数とか検定とか統計的とか・・いろんな専門用語が登場して分かりにくいですよね。

いきなりお腹いっぱい
それぞれ基礎知識を理解しておく必要があるので、ひとつずつ説明していきます。
相関係数
まず相関係数について、相関係数とは2つの変数間の直線的な関係の強さを表した指標のことで、以下の式で求めることができます。
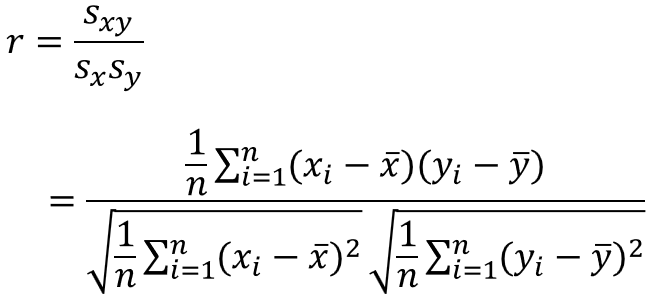
$r$は相関係数、$s_{x}$は$x$の標準偏差、$s_{y}$は$y$の標準偏差、$s_{xy}$は$x$と$y$の共分散を表します。
また、分母と分子を$1/n$で割ると、次のように表すこともできます。
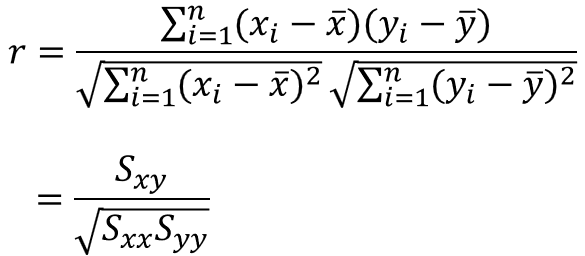
ここで$S_{xx}$は$x$の偏差平方和、$S_{yy}$は$y$の偏差平方和、$S_{xy}$は$x$と$y$の偏差の積です。
標準偏差では小文字の$s$、偏差平方和では大文字の$S$を用いるのが一般的なので、混同しないように意識しておきましょう。
相関係数$r$は、-1~1の範囲を取る無次元の値で、$r$の絶対値が大きいほど変数どうしの関係が強いことを表しています。
詳しくは以下の記事で紹介していますので、合わせてご覧ください。

統計的検定
次に統計的検定について、統計的検定とは母集団に関して立てたとある仮説が成立するか否か、標本データから確率論的に結論を導き出す手法のことです。
ここで仮説というのは、「○○=△△」や「○○>△△」といった数式で表せるものであり、例えば標本平均$\bar{μ}$と母平均$μ_{0}$が等しいか否か調べたい場合には、「$\bar{μ}=μ_{o}$」と設定します。
仮説には、帰無仮説と対立仮説の2種類があります。
帰無仮説とは、無に帰することを期待した仮説という意味で帰無仮説と呼ばれ、$H0$と表記されます。
検定を行う上では、まず最初に帰無仮説を設定するところから始めます。
先ほどの例で挙げた、「$\bar{μ}=μ_{o}$」も帰無仮説に該当します。
一方で対立仮説$H1$とは、検定統計量が一定の範囲内に収まらない(=帰無仮説が棄却された)場合に採択される仮説で、調べたい本来の目的の仮説のことです。
例えば、上記の$H0$に対する対立仮説は、「$\bar{μ}≠μo$」と設定します。
この場合、「標本データと母集団の平均値が等しいとは言えない」ことが対立仮説となります。
なお、検定統計量とは帰無仮説の棄却/採択の判定基準となる指標のことで、標準正規分布やt分布などから検定統計量に対応する発生確率を求めることができます。
詳しくは以下の記事で解説していますので、合わせてご覧ください。

無相関の検定
さて、予備知識を理解できたところで、いよいよ無相関の検定とは何か説明します。
あらためて記載すると、無相関の検定とは相関係数に意味があるのか統計的に調べる手法のことです。
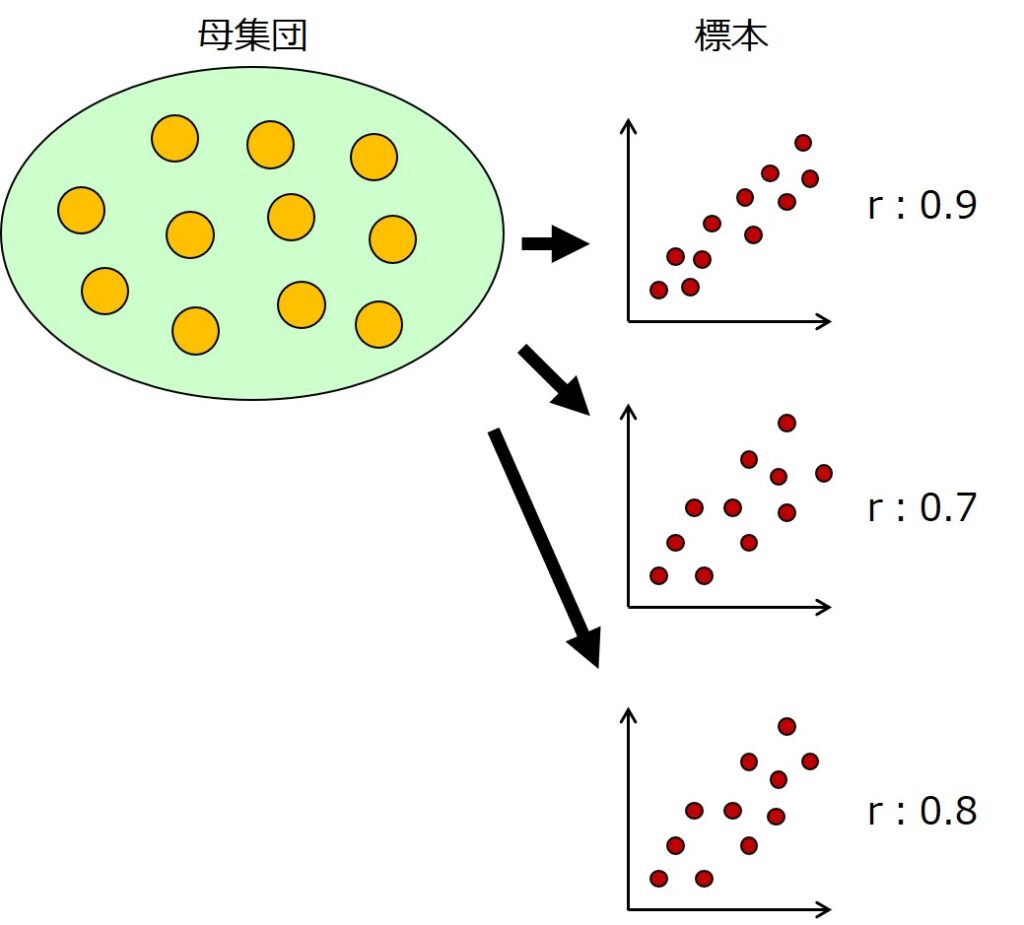
相関係数の検定というとピンとこないかもしれませんが、相関係数を求めるためのデータも母集団からサンプリングした標本であり、どの標本を抜き取るかによって相関係数の値が変わってきます。
例えば、実は母集団には相関がないのに、たまたま抜き取ったサンプルの相関があるように見えることがあります。
しかし、ランダムに抜き取った場合、確率的に最も起こりやすいのは母集団と同じ傾向であり、母集団と異なる傾向のサンプルを抜き取る確率は低いと考えられます。
そのため、統計的検定の考え方を用いて、どのくらい起こりにくい確率のものか定量的に判定しようというものなのです。

基準がはっきりしていると分かりやすいね
目的・メリット
客観的な指標で判定できる
統計的検定により、相関係数の有意性を客観的に判定できることが無相関の検定の一番の目的であり、メリットでもあります。
相関係数は絶対値の大小で以下のように相関の有無を大まかに見ることができます。

しかし、例えば相関係数が0.9と0.8の場合で、信頼性がどの程度変わるのか定量的に捉えることは難しいと思いませんか。
もちろん、信頼度が90%とか80%といったように単純な比例計算に置き換えられるものではありません。
無相関の検定では、相関係数を検定統計量に変換することで、確率としての定量値に表すことができ、直感的な信頼度と結び付けやすくなる効果があります。
データ数の影響を補正できる
相関係数の注意点としては、同じ相関係数の値でもデータ数の大小によって有意性が全く変わってくることです。
例えば、データが5つしかない場合と、100個のデータから相関係数を求めた場合、同じ値でもどちらの信頼性が高いか、感覚的にも理解できますよね。
無相関の検定では、相関係数とデータ数から検定統計量を算出して指標とするので、データ数の違いによる影響を補正して指標に表すことができます。
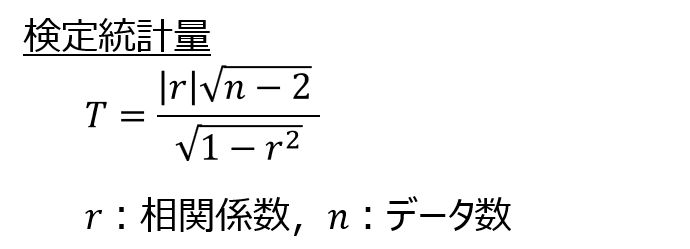
無相関の検定のやり方
それでは、実際に例題を用いて、無相関の検定をやってみましょう。
例題
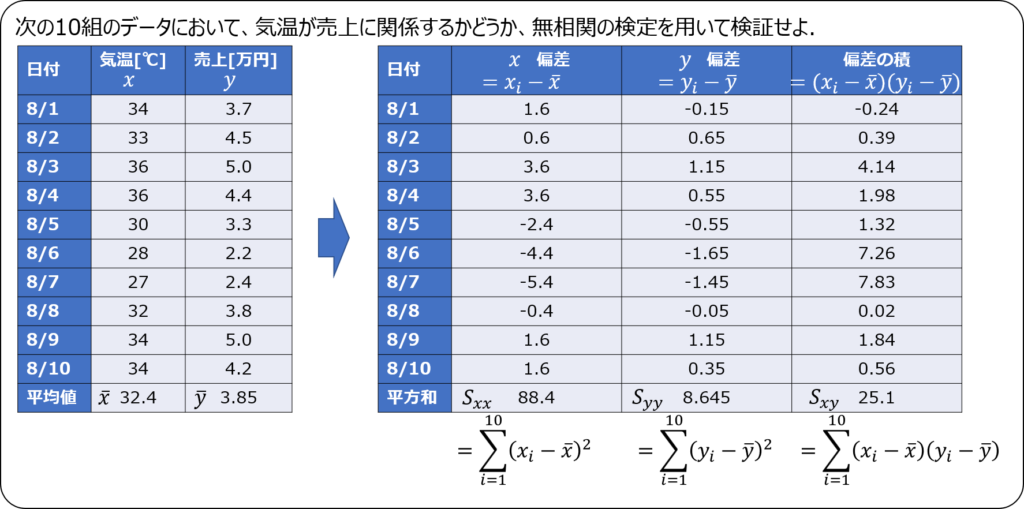
帰無仮説を設定する
まず、帰無仮説を設定します。
無相関の検定では、「母集団の相関係数はゼロである」ことを帰無仮説とします。
ここで疑問に思うのが、相関があることを示したいのに、なぜ相関があることを帰無仮説にせずに、あえて相関係数がゼロであることを仮説にするのか?という点です。
その理由はシンプルで、「相関がある」ことを証明することが非常に困難であるからです。
相関があるというのは、相関係数が0.5場合や0.9の場合といったように、ありとあらゆるケースが想定されます。
これらを帰無仮説にすると、否定するための根拠(反例)を十分に示すことができず、結論にたどり着くことができません。
そのため、相関係数がゼロであることを帰無仮説にすれば、相関係数がゼロとなる確率が限りなく低いことを示すことで、反対に相関がある確率が高いことを証明することができるのです。
このような考え方を「背理法」と呼び、統計的検定では基本的にこの考え方を用いて帰無仮説と対立仮説を設定しているのです。
帰無仮説$H_{0}$:母集団の相関係数はゼロである
対立仮説$H_{1}$:母集団の相関係数はゼロとは言えない
検定統計量を求める
検定の考え方が理解できたところで、検定統計量を以下の式により求めます。
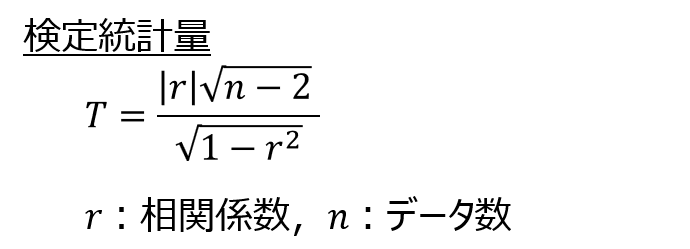
$r$は相関係数を表し、$n$はデータ数を表します。分子の${|r|}$は絶対値を表す記号です。

相関係数とデータ数だけで計算できるので、非常にシンプルですね。
相関係数が高いほど、またデータ数が多いほど検定統計量の値が大きくなり、すなわち確率的に相関係数がゼロである事象が起こりにくいことを意味します。
有意性の有無を判定する
検定統計量が求められたら、最後に有意性の有無をt検定により判定します。
t分布表を用いれば、帰無仮説の棄却/採択の判定値を読み取ることができるので、これと検定統計量の大小関係をチェックします。
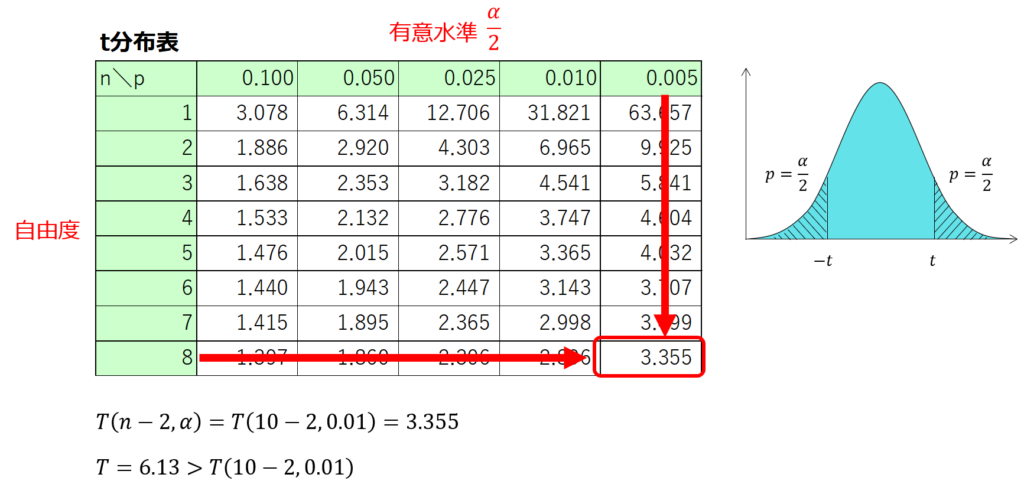
今回の例題の場合、1%の有意水準で相関係数に意味があると判定されました。
なお、t検定については、以下の記事で詳しく解説していますので、合わせてご覧ください。

検定統計量の定義の証明
最後に、無相関の検定における検定統計量の導出のしかたについて説明しておきます。
たびたび登場しますが、検定統計量は以下の式で表されます。
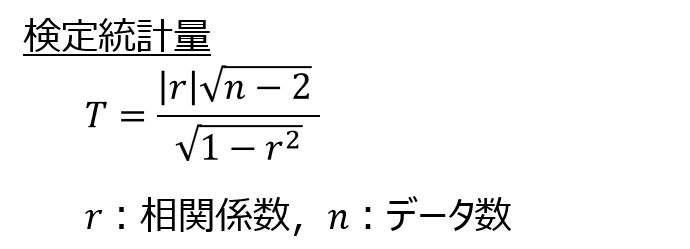
なぜ、このような数式になるのでしょうか。
変数どうしの関係性を分析する際、相関係数として指標に表す他に、要因となる変数から結果となる変数を一つの関係式(回帰式)で表す方法があります。

そして、回帰式の推定精度を図る方法として分散分析が用いられ、以下のように回帰式で説明できる成分と誤差成分の比率から統計的検定のできる指標に表しているのです。
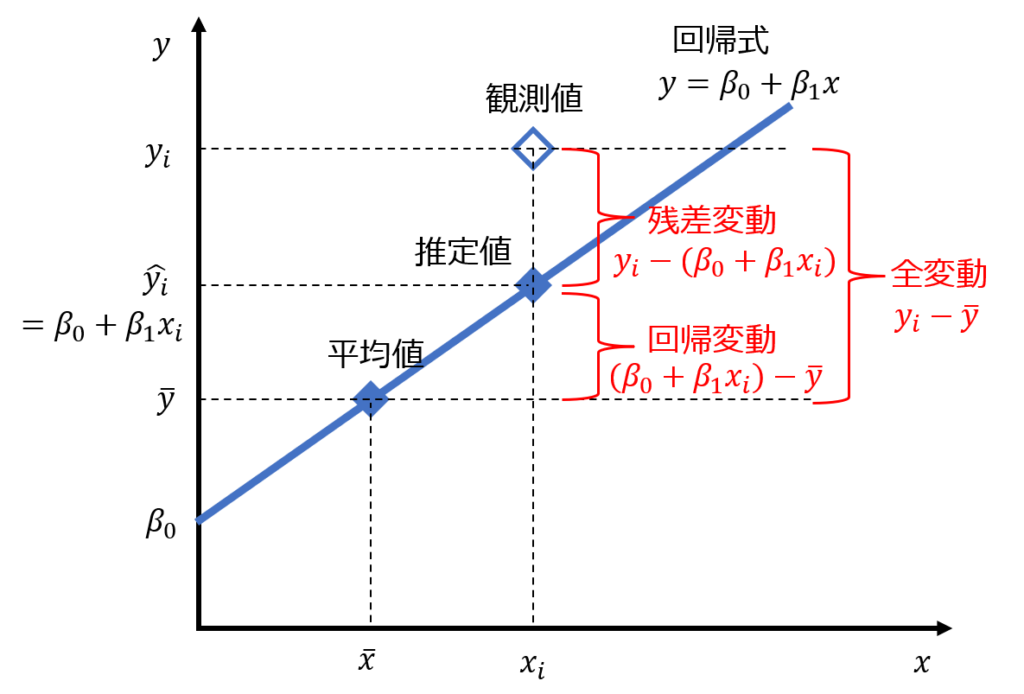
具体的には、回帰変動と残差変動の分散比をF検定で検定しており、無相関の検定でも同様の考え方が当てはめられるのです。
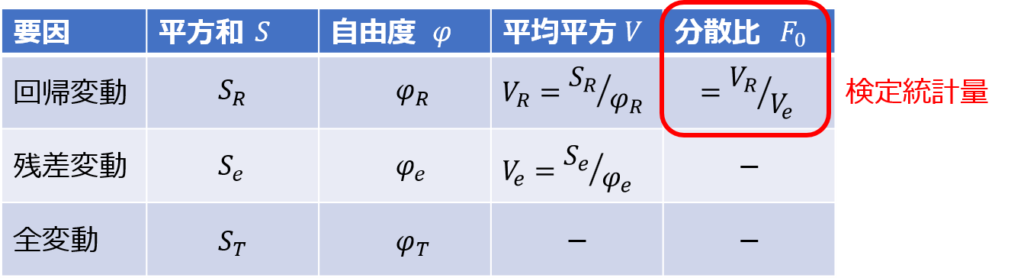
では、回帰分析と同様にF検定で相関係数の有意性が判定できるとして、検定統計量の式の導出に至る過程を以下に示します。

ここで、F分布はt分布の二乗として表される性質を利用すると、さらに以下のように変換することができます。
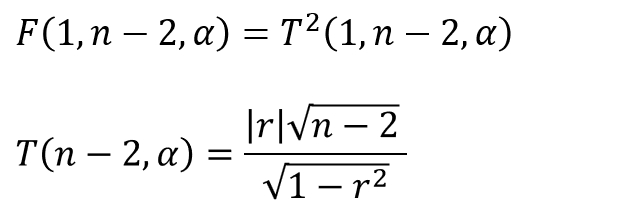
以上により、無相関の検定の検定統計量を分散分析の考え方から導き出すことができました。

元々は分散分析と同じ考え方なんだ

まとめ
- 無相関の検定(無相関検定)
相関係数に意味があるのか統計的に調べる手法のこと - 目的・メリット
・客観的な指標で判定できる
・データ数の影響を補正できる - 無相関の検定のやり方
・帰無仮説を設定する(母集団の相関係数はゼロ)
・検定統計量を求める
・有意性の有無をt検定で判定する
最後までご覧いただきありがとうございました。
まずは相関分析の基本から始めたい方に。
相関分析から単回帰・重回帰分析まで幅広く。
多変量解析マスターを目指すなら。




コメント