「回帰分析って何? 相関分析とどう違うの?」
「回帰式の求め方について手順を踏んで理解したい」
「分散分析表の作り方がさっぱり分からない」
このような疑問や悩みをお持ちの方に向けた記事です。
回帰分析や分散分析って、言葉を聞くだけで難しそうで、敬遠したくなりますよね。
しかし、いずれも計算自体は特に難しいものでもなく、回帰分析の目的や定義の式をきちんと理解しておけば、心配する必要はありません。
この記事では、回帰分析の目的とメリット、単回帰分析の回帰式の求め方、分散分析の考え方について、手順を追って解説しています。
ぜひ、最後まで読んで参考にしていただければと思います。
回帰分析とは?
回帰分析とは、要因となる変数と結果となる変数の関係性を明らかにし、両者の変数を一つの関係式に表す統計的手法のことです。
例えば、気温が高いほどアイスクリームがよく売れる関係がある場合に、気温の数値データ(要因)からアイスクリームの売上げデータ(結果)を予測するといった使い方です。
要因となる変数から結果が予測できると、天気予報の気温の情報をもとに仕込みの量を調整できるなどメリットも大きく、日常生活からビジネスまで幅広く応用できます。
回帰分析では、$y=ax+b$といった数式で表されるように、$x$の値から$y$を推定することを目的としており、入力値である$x$を説明変数、出力値である$y$を目的変数と呼びます。
説明変数は必ずしも1つである必要はなく、2つ以上の変数で構成することも可能です。
説明変数が1つの場合を単回帰分析、2つ以上の場合を重回帰分析と呼び、重回帰分析は多次元の変数を取り扱う多変量解析の一種と言えるのです。

まずは単回帰分析からマスターしよう
目的・メリット
説明変数から目的変数を予測する
まず、回帰分析の一番の目的は、目的変数(結果)を予測できることと言えるでしょう。
先ほどのアイスクリームの事例でも挙げたように、とある変数から結果を推定できることは非常にメリットが大きく、労力・時間・お金など多くの要素を節約して効率化できます。
特に、回帰式に表すことで、実際に取得したデータ以外の点についても連続的に推定値を計算でき、説明変数の任意の値に対応する結果の推定値を得ることができます。
関係の強さを定量的に表す
説明変数と目的変数の関係の強さを相関係数や寄与率(決定係数)として定量的に表すことで、客観的な指標として扱うことができます。
例えば、A地点とB地点の気温に対して、どちらがよりアイスクリームの売上げと強い関係性があるのか検証したい場合など、相関係数を見ることで容易に比較できます。
関係式の有意性を統計的に判断できる
説明変数と目的変数のデータから得られた回帰式は、推定の精度が高くないと意味がありません。
後ほど詳しく説明しますが、分散分析では回帰式の有意性の検証を統計的に行うもので、F分布を用いて精度の高さを機械的に判断することができます。
相関分析との違い
回帰分析と似た言葉として、相関分析という手法があります。
相関分析とは、要因どうし、または要因(原因)と特性(結果)の関係性を統計的かつ定量的に分析する手法のことです。
相関分析の特徴としては、主に以下の3つが挙げられます。
・変数どうしの因果関係は仮定しない
・取り扱う変数は2つで、一対一で比較する
・変数どうしの直線的な関係の強さを調べる
回帰分析では説明変数と目的変数の関係のように因果関係を仮定しますが、相関分析では必ずしも因果関係がある必要はなく、単に要因どうしの関係性を見ることも含まれます。
また、回帰分析では重回帰分析のように多くの変数を扱うことができますが、相関分析では変数2つに対して一対一で直線的な関係性を見ることに限られます。
次のように、それぞれの特徴を対比して覚えておくとわかりやすいと思います。


単回帰分析の回帰式の求め方
回帰係数の定義
ここまで、回帰分析の定義について説明しましたが、以降では実際に例題を用いて回帰式を求めてみましょう。
まず用語の定義として、以下の式で表される回帰式における係数$β_{0}$と$β_{1}$を回帰係数と呼び、グラフの傾きにあたる要素を$β_{1}$、縦軸と交差する切片の値を$β_{0}$と表記します。

単回帰分析の場合、説明変数が一つで二次元のグラフに表現できるため、回帰式のイメージが付きやすいですね。
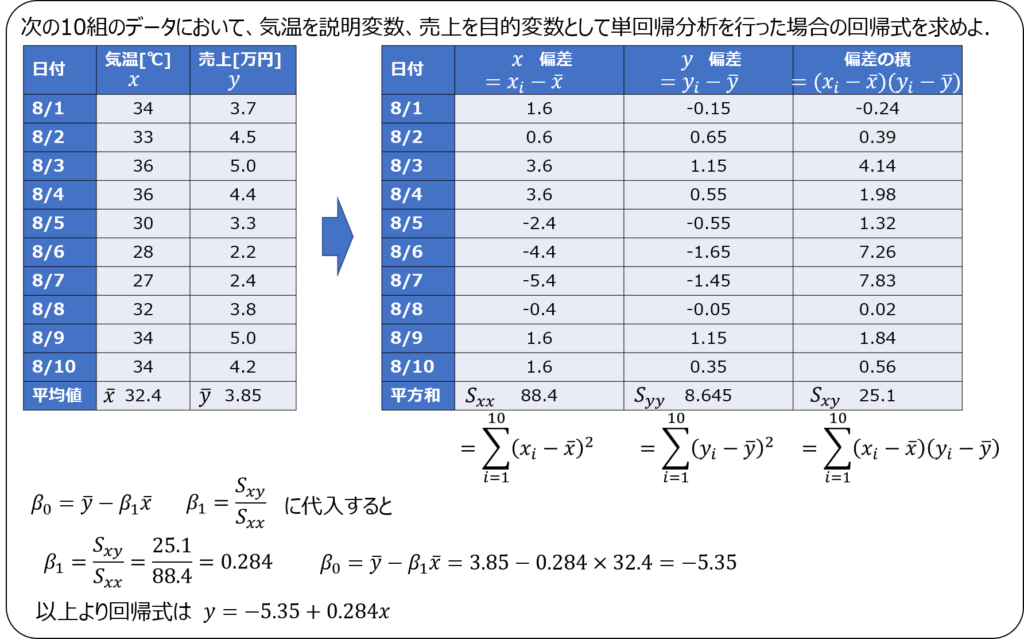
ここで、$β_{0}$と$β_{1}$は以下の式で計算することができます。


偏差の積と平方和を求めれば、あとは簡単だね
定義の式の証明
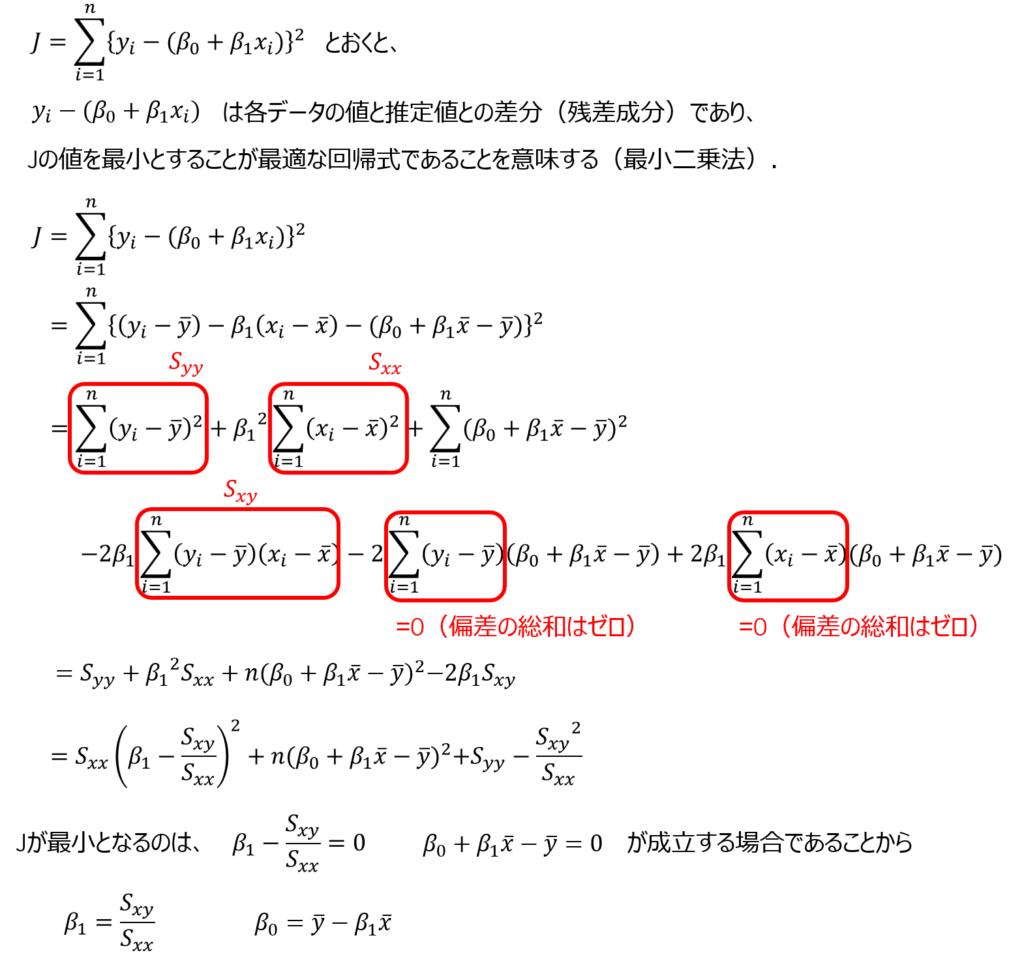
上記の通り、$β_{0}$と$β_{1}$の計算式は非常にシンプルで覚えやすいものですが、なぜこのような形になるのか、定義の式を導出してみました。
少し複雑ですが、興味のあるかたは、いちど目を通してみてください。
例題
分散分析とは?
目的
さて、回帰式の導出まで無事にたどり着けたところで、これで単回帰分析がお終いではありません。
得られた回帰式が意味のある精度であるものか、検証が必要なのです。
例えば、次の2つのデータの回帰式を得たとします。
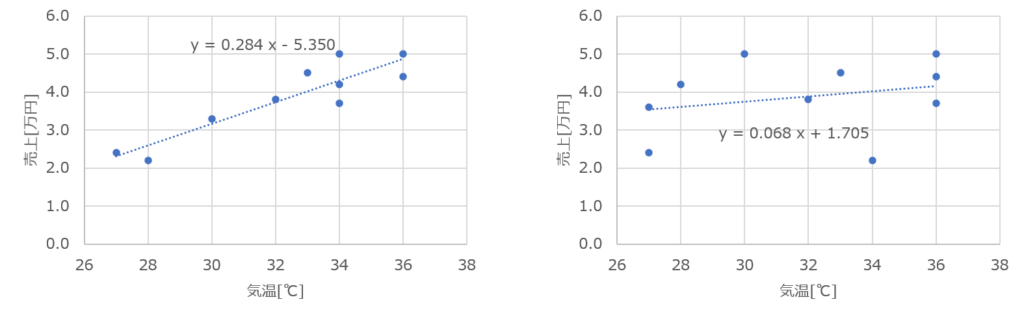
どちらの回帰式の推定精度が高そうか、グラフから直感的に判断できますよね。
このように、グラフに表現できれば視覚的に理解できますが、重回帰分析のように説明変数が2つ以上あると、グラフ以外の手段で回帰式の精度を検証しなければなりません。
分散分析とは、回帰式の有意性を統計的に検証するための手法で、回帰分析の一環として、必ず回帰式の導出とセットで確認することを意識しておきましょう。
考え方
分散分析では、回帰変動と残差変動の分散比を見ることで、回帰式の精度を検証することができます。
全変動:実際のデータと全体の平均値との差
回帰変動:回帰式から得られた推定値と全体の平均値との差
残差変動:実際のデータと回帰式から得られた推定値との差
全変動=回帰変動+残差変動
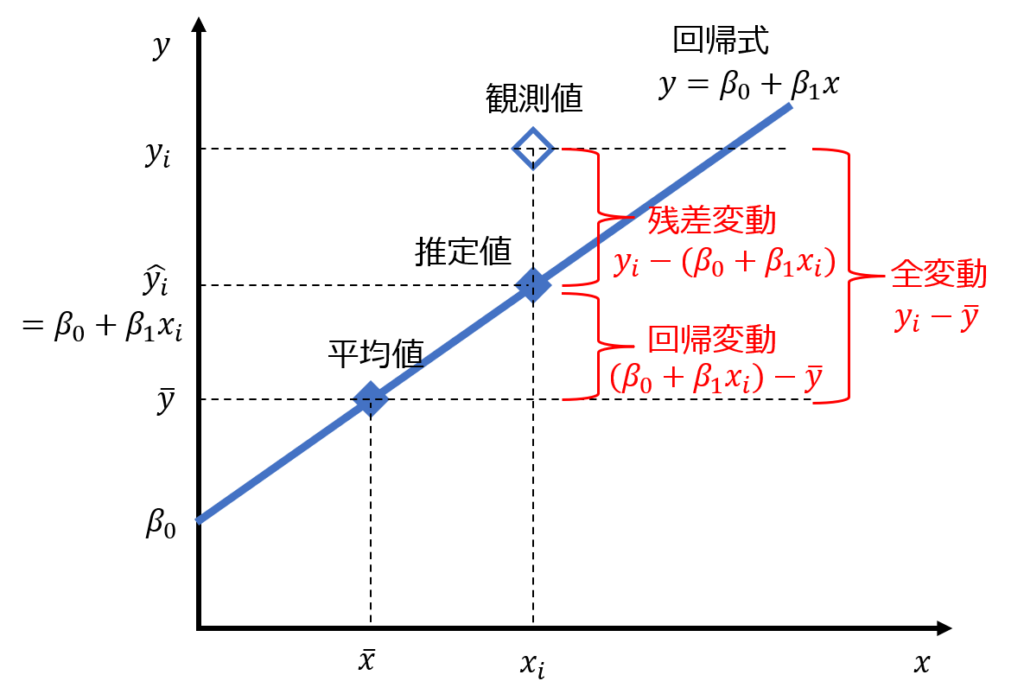
回帰変動とは回帰式で説明可能な変動の成分、残差変動とは説明ができない成分のことで、回帰変動の割合が高いほど回帰式の精度が高いことを意味します。
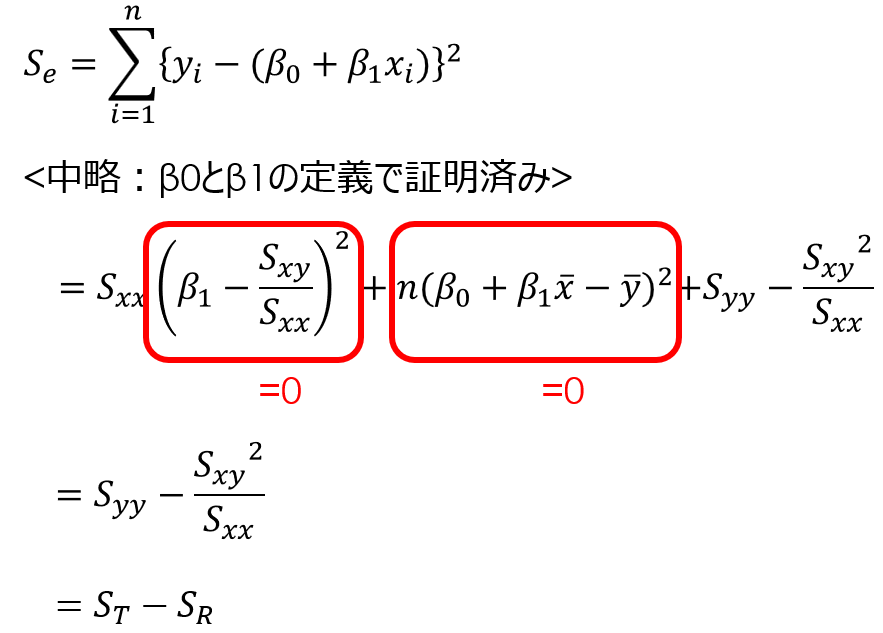
ここで、残差変動の式に注目すると、先ほどの回帰係数の証明の式で登場した残差成分と同じ形であることが分かります。
回帰係数の証明の式で残差変動を二乗にしたのは、単なる総和をとってしまうとプラスとマイナスで誤差がキャンセルされてしまうためです。
そのため、分散分析でも残差変動の二乗の総和を小さくすることが指標として適切であり、同じように回帰変動や全変動についても二乗の和で判定します。

平方和がゼロになるのは、全ての残差がゼロの時だからね
全変動の平方和$S_{T}$、回帰変動の平方和$S_{R}$は以下の式で定義されます。

また、$S_{T}$、$S_{R}$、$S_{e}$(残差変動の平方和)には、以下の関係式が成り立ちます。
$S_{T}=S_{R}+S_{e}$
少し不思議な感じがしますが、単純に足し合わせても、全変動=回帰変動+残差変動となりますが、平方和どうしも同じ関係が成り立つのです。
なお、分散分析では各変動の平方和をそのまま判定指標に用いると、サンプルサイズの違いのよる影響を受けるため、適切ではありません。
そこで、それぞれの変動を自由度で割って「分散」を計算し、分散の比率(分散比)を検定統計量とすることで、標準化して有意性を判別できるようになるのです。
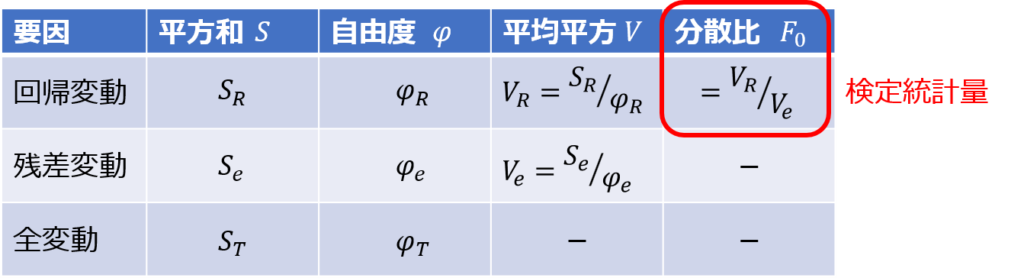
分散比の検定には、F分布を用います。
F分布とF検定については、以下の記事で詳しく解説していますので、合わせてご覧ください。


分散分析の手順
先ほどの例題のデータを用いて、分散分析表を実際に作ってみましょう。
各変動の平方和を求める
回帰変動$S_{R}$、残差変動$S_{e}$、全変動$S_{T}$について、それぞれ平方和を求めます。
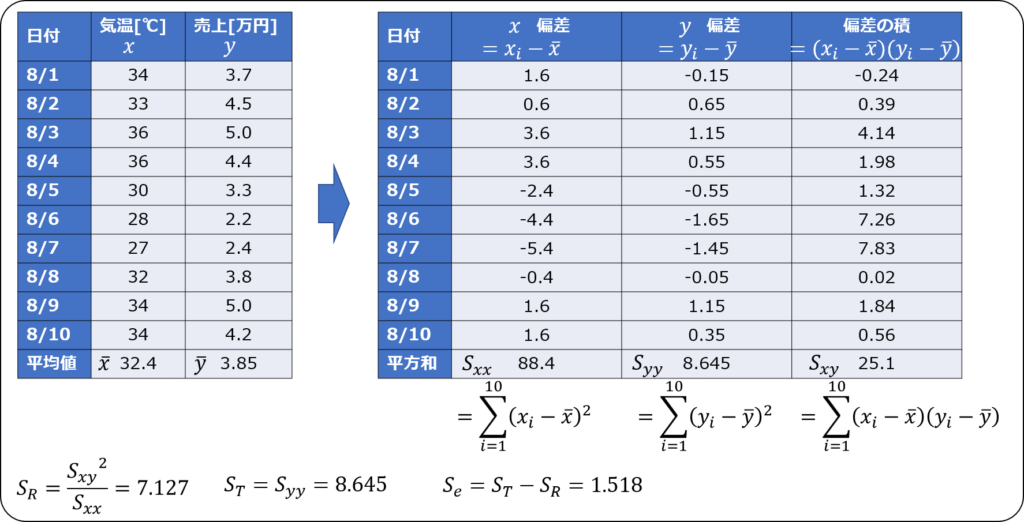
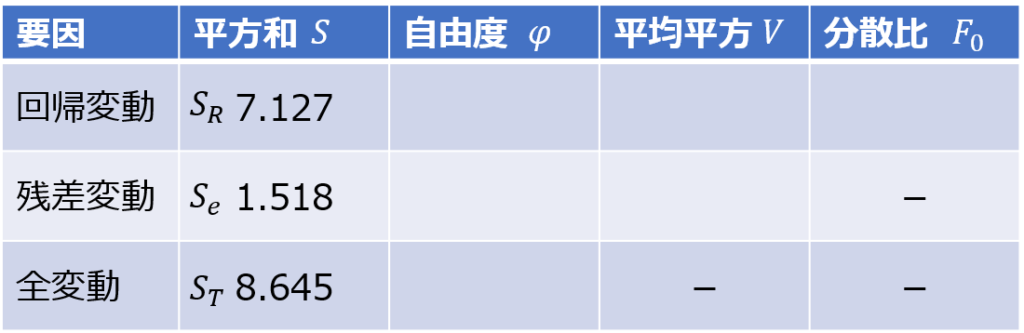
自由度を入れる
分散分析表に各成分の自由度を入れます。
全変動の自由度:(データ数)-1
回帰変動の自由度:(説明変数の数)
残差変動の自由度:(全変動の自由度)-(回帰変動の自由度)
分散を計算する
各変動の値を自由度で割って、それぞれの分散を求めます。
分散比を求める
回帰変動の分散を残差変動の分散で割って、分散比を求めます。
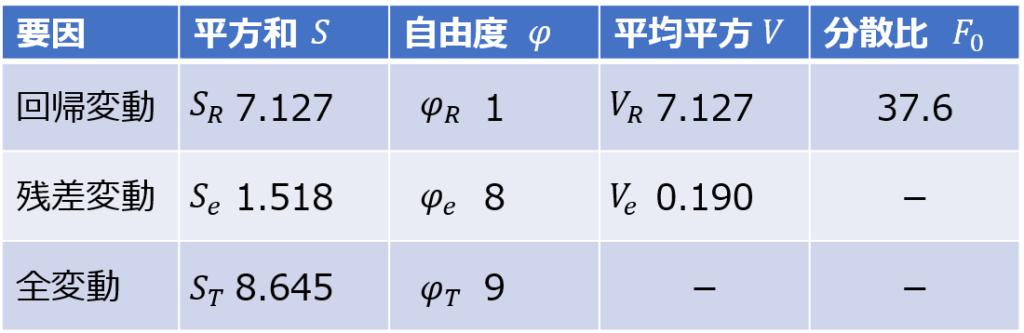
F分布で有意性を検定する
得られた分散比を検定統計量として、F分布の有意性を検定します。
回帰変動の自由度を第一自由度、残差変動を第二自由度として、F分布表から棄却域となる判定値を読み取ります。
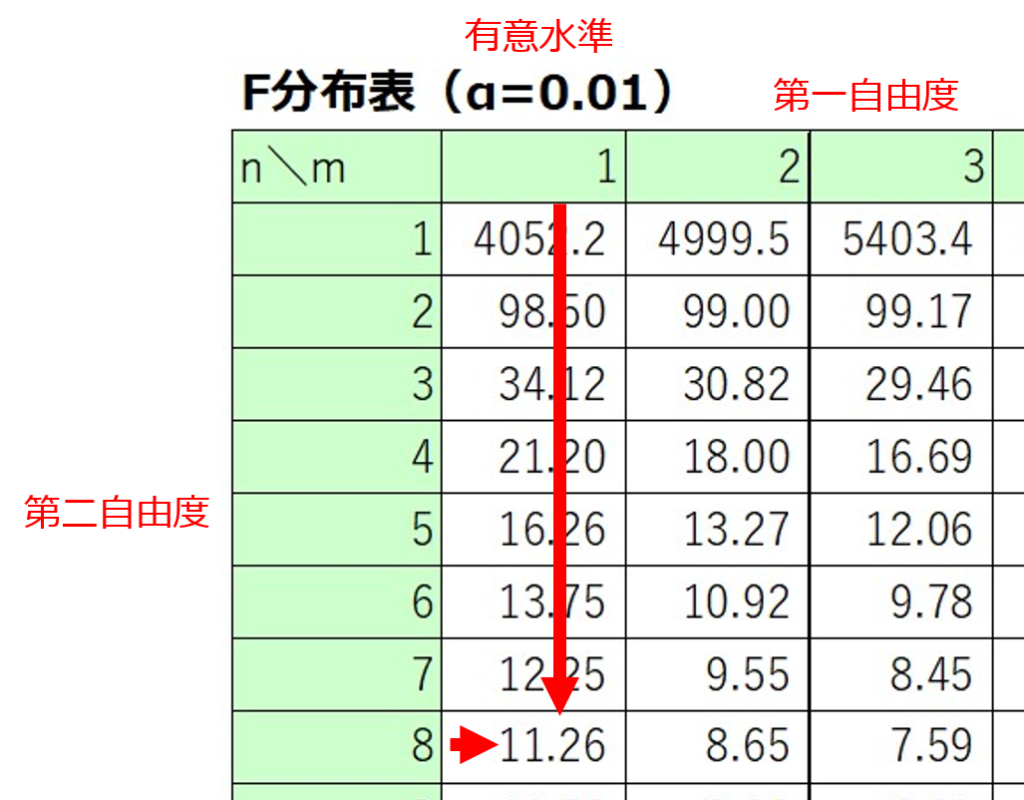
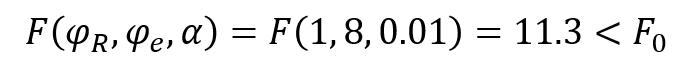
今回の例では、検定統計量である分散比が1%の判定値を超えているので、1%有意水準で回帰式に意味があるという結果になりました。
まとめ
- 回帰分析
要因となる変数と結果となる変数の関係性を明らかにし、両者の変数を一つの関係式に表す統計的手法 - 目的・メリット
・説明変数から目的変数を予測する
・関係の強さを定量的に表す
・関係式の有意性を統計的に判断できる - 分散分析
回帰式の有意性を統計的に検証するための手法 - 分散分析の手順
・回帰変動、残差変動の平方和を求める
・平方和を自由度で割って分散を求める
・回帰変動の分散を残差変動の分散で割った分散比を求める
・分散比を検定統計量として、F分布で有意性を検定する
最後までご覧いただきありがとうございました。
まずは相関分析の基本から始めたい方に。
相関分析から単回帰・重回帰分析まで幅広く。
多変量解析マスターを目指すなら。




コメント