「相関分析って何? 回帰分析と何が違うの?」
「エクセルでの相関係数の求め方を知りたい」
「相関分析を行う上での注意点は?」
このような疑問や悩みをお持ちの方に向けた記事です。
相関というと何となく関係性があることかな?くらいのイメージを持った方も多いかもしれませんが、「相関分析」と表現すると急にむずかしそうな雰囲気が漂います。
ただ、実際にやっていることはシンプルで、いちど基本から覚えてしまえば、勝手に苦手意識を持つ必要はありません。
この記事では、相関分析の目的と実践する上での注意点、相関係数と寄与率の定義、エクセルを用いた相関係数の求め方3つについて紹介します。
ぜひ、最後まで読んで参考にしていただけると幸いです。
相関分析とは?
相関分析とは、要因どうし、または要因(原因)と特性(結果)の関係性を統計的かつ定量的に分析する手法のことで、日常生活やビジネスまで幅広く活用される考え方です。
例えば、A地点とB地点の気温の関係性を調べることも相関分析の一つです。
日ごとに両地点の気温データを取得し、A地点の気温の高い日はB地点でも高い関係が見られれば、正の相関関係があるといった表現をします。
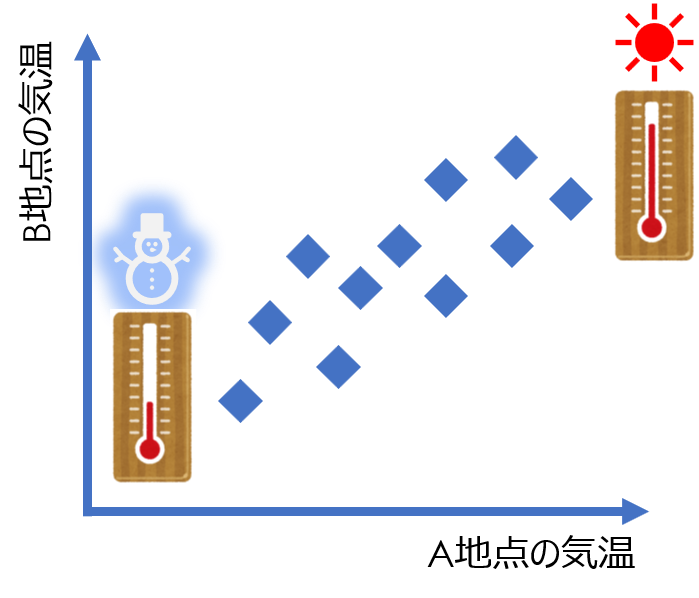

関係性を調べることは身近な例も多いね
相関分析の特徴としては、主に以下の3つが挙げられます。
- 変数どうしの因果関係は仮定しない
- 取り扱う変数は2つで、一対一で比較する
- 変数どうしの直線的な関係の強さを調べる
変数どうしの因果関係は仮定しない
相関分析では、比較する変数どうしの因果関係は問いません。
例えば、気温が高いからアイスクリームが良く売れる場合などは、2つの変数間に原因と結果の関係性があり、2つの変数が逆になると因果関係が成立しなくなります。
一方、A地点とB地点の気温は、それぞれ地理的に大きく離れた箇所であれば、どちらかの気温がもう片方に影響を受けることは考えにくく、因果関係はありません。
このような場合においても関係性の有無を調べることは相関分析に該当し、後に説明する回帰分析と異なる特徴の一つなので、覚えておきましょう。
取り扱う変数は2つで、一対一で比較する
相関分析で取り扱う変数は2つが原則です。
例えば、A地点、B地点、C地点の気温の関係性を見たい場合には、A vs B、B vs C、C vs Aといったように、それぞれ一対一で関係の強さを示します。
相関行列のように、多くの変数を一度に取り扱う場合においても、相関係数の値ひとつずつに着目すれば、一対一での関係を表しており、結局は変数が2つの場合と同じです。
変数どうしの直線的な関係の強さを調べる
ここまで、「関係の強さ」と表現しているのは、あくまで変数間に直線的な関係があるか否かです。
一方の変数が大きくなった際にもう一方も同じ動きをして大きくなると正の相関、もう一方の変数が逆の動きをして小さくなると負の相関となります。
また、相関関係は散布図にプロットした点が一直線に重なった場合が最も強く、つまり直線的な関係の強さのことを表しています。
仮に、散布図の分布形状から曲線的な関係が強く見られたとしても、相関分析では関係の強さを表すことができませんので、注意しておきましょう。
目的・メリット
関係性を見つける
大量のデータを扱う場合、情報量が多すぎて、反対にデータが数字の羅列にしか見えなくなってしまうことがあります。
これでは、せっかく苦労して取得したデータも十分に活かされません。
最初から相関行列を作成して、それぞれの要因(パラメータ)の相関係数を一挙に計算し、数値で判断する方法もありますが、これには統計学の豊富な知識と経験が必要です。
まずは、関係性の強そうな主要なパラメータを絞り込む目的で、散布図にするだけでも視覚的に関係有無の大まかな傾向を掴むことができます。
関係の強さを定量的に表す
相関分析のもう一つの目的は、関係性の強さを数値で表現することです。
関係が強い、弱いといっても、どの程度で解釈するかは、人それぞれの感覚に依存します。
このような認識の食い違いをなくすため、相関係数や寄与率といった統計的な指標を用います。
後述しますが、いまやエクセルを使えば、変数間の相関係数を一瞬で求めることができるので、データを定量的に分析することを心がけましょう。
回帰分析との違い
相関分析と似た言葉として、回帰分析というものがあります。
回帰分析では、$y=ax+b$といった数式で表されるように、$x$の値から$y$を推定することを目的としており、入力値である$x$を説明変数、出力値である$y$を目的変数と呼びます。
先ほどの相関分析と対比すると、回帰分析の特徴は次のようになります。

回帰分析では、説明変数と目的変数の間に因果関係を仮定し、その仮定が有意なものか否か、分散分析表とF検定で統計量を用いて検証します。
また、説明変数は必ずしも1つである必要はなく、2つ以上の変数で構成することも可能です。
説明変数が1つの場合を単回帰分析、2つ以上の場合を重回帰分析と呼び、重回帰分析は多次元の変数を取り扱う多変量解析の一種と言えるのです。
このように、相関分析と回帰分析は取り扱うデータの種類は似ていますが、目的や変数の性質が異なるので、セットで覚えておきましょう。

似て非なるものなり
相関分析のやり方
それでは、具体的な相関分析のやり方として、2つの手法を紹介します。
散布図から傾向を読み取る
ひとつめは、関係性を調べたい2つの変数を縦軸と横軸に取って散布図にし、プロットした点の分布から傾向を読み取る方法です。
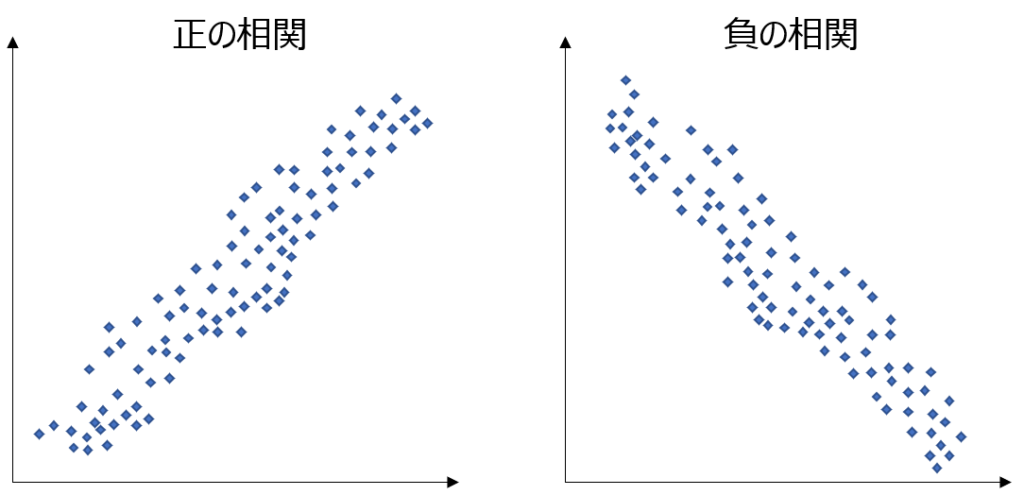
シンプルかつ手間もかからないやり方ですが、グラフにして視覚的に表すことで、大まかな傾向を瞬時に捉えることができます。
また、異常点などの外れ値や、データの偏りを見つけ出すことも容易で、視覚的に表現することの強みと言えます。
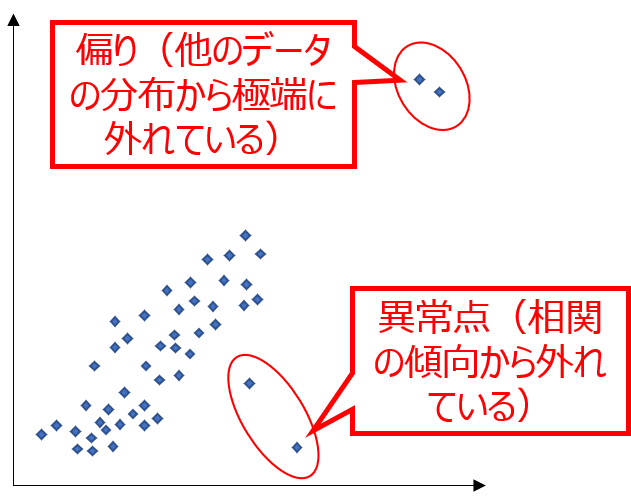
エクセルでの散布図の書き方は次の通り。
データを行列に整理してセルに入力する
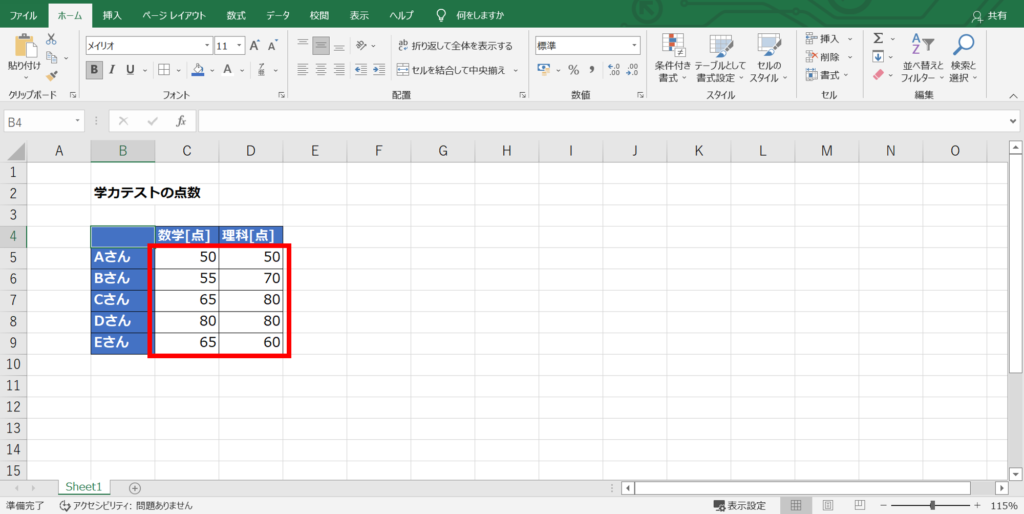
データ範囲を選択して「挿入」⇒「グラフ」から散布図を選択する
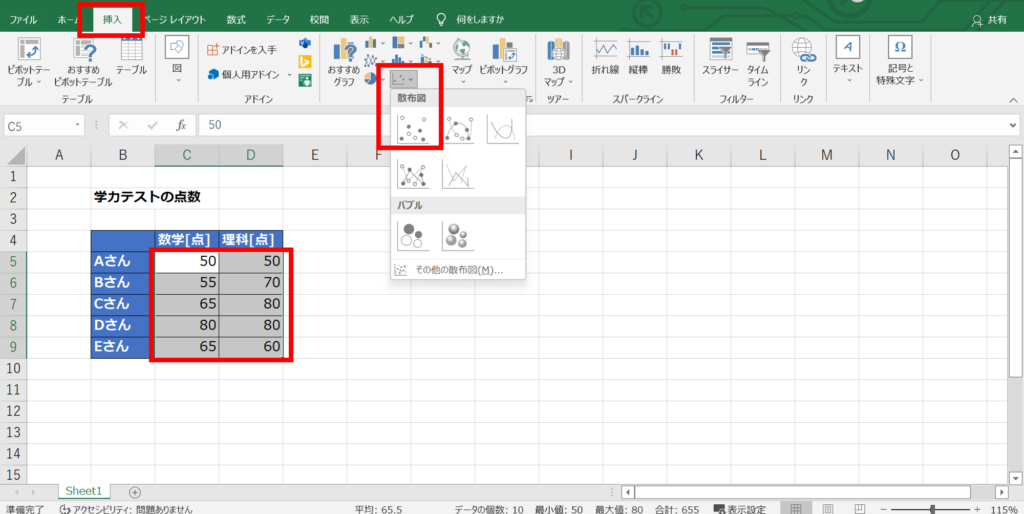
データ範囲が意図した通りにならない場合は、グラフを右クリックしてデータ範囲を手動で修正する。
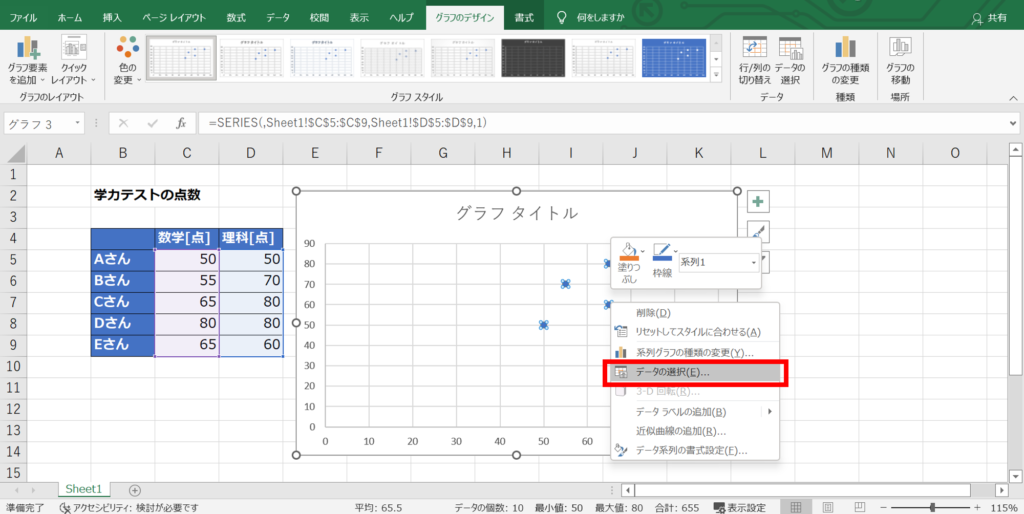
相関係数で定量的に表す
もう一つは、相関係数として2つの変数間の関係の強さを統計量として表すことです。
散布図では判断できない微妙な違いや大小関係の順位付けをしたい場合など、定量的に数値で表すことのできる相関係数はとても便利です。
また、相関係数を二乗した値を寄与率(決定係数)と呼び、データの全情報のうち、回帰式で説明が可能な情報量の比率を表します。
回帰分析でも活用する指標ですので、定義と計算方法は必ず押さえておきましょう。
相関係数と寄与率の定義
相関係数とは、2つの変数間の直線的な関係の強さを表した指標のことで、以下の式で求めることができます。
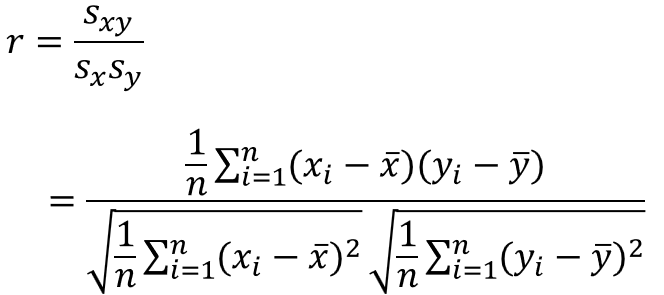
$r$は相関係数、$s_{x}$は$x$の標準偏差、$s_{y}$は$y$の標準偏差、$s_{xy}$は$x$と$y$の共分散を表します。
また、分母と分子を$1/n$で割ると、次のように表すこともできます。
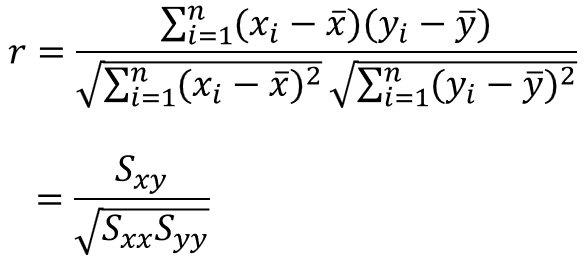
ここで$S_{xx}$は$x$の偏差平方和、$S_{yy}$は$y$の偏差平方和、$S_{xy}$は$x$と$y$の偏差の積です。
標準偏差では小文字の$s$、偏差平方和では大文字の$S$を用いるのが一般的なので、混同しないように意識しておきましょう。
相関係数$r$は、-1~1の範囲を取る無次元の値です。
では、相関係数が1というのは、どのような場合を表すのでしょうか。
先ほどの数式で$r=1$と置くと、以下のように変換できます。
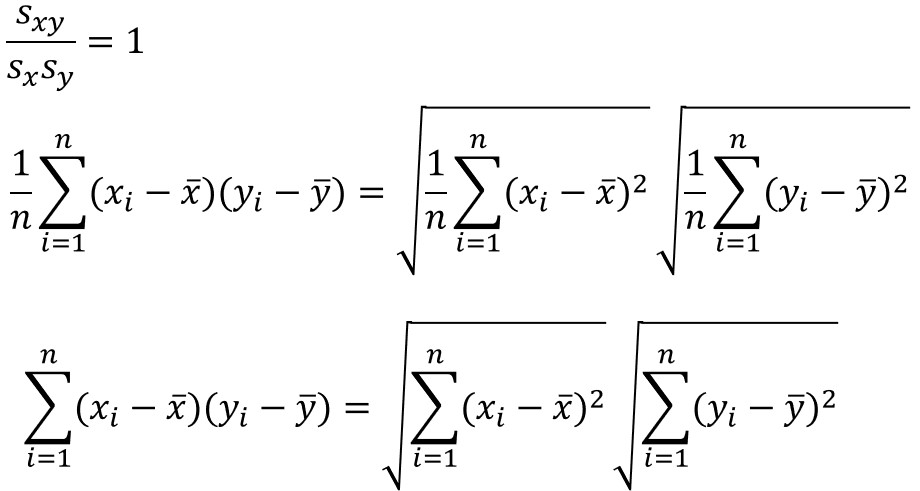
この数式は、コーシー・シュワルツの不等式を用いれば、意味を理解することができます。
コーシー・シュワルツの不等式とは、以下の関係が成り立つ性質を表したものです。

相関係数の式に置き換えると、等号成立条件は以下のように表されます。
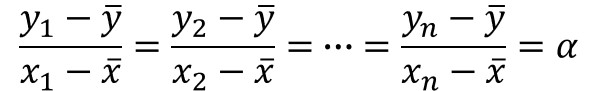
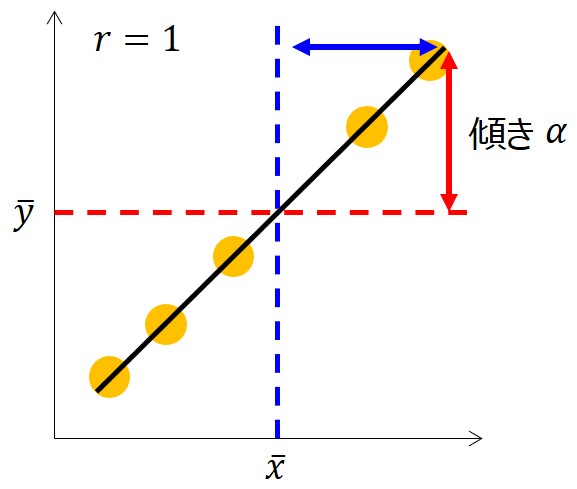
$\bar{x}$、$\bar{y}$を原点にシフトした座標系を$\acute{x}$、 $\acute{y}$とすると $\acute{y}= α\acute{x}$と表すことができ、すなわち、$\bar{x}$、$\bar{y}$を原点に全てのデータが一直線に並んだ状態のことを意味します。
また、相関係数の値と関係性の強さの対応は次のように表現されます。
値の大よその目安として覚えておくと便利です。

なお、共分散の意味やエクセルを使った求め方については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

寄与率(決定係数)$R^{2}$は、以下の定義の式で表されます。

残差変動は、実際のデータと回帰式から得られた推定値との差を表します。
また全変動は、実際のデータと全体の平均値との差を表します。
つまり、残差変動を全変動で割った値というのは、回帰式で得られた誤差成分の比率の大きさを意味しており、誤差の比率が0に近いほど回帰式の精度が良いことを表しています。
なお、数式の導出は回帰分析の記事で詳しく説明しますが、寄与率は相関係数の二乗と同じ式に変換できます。
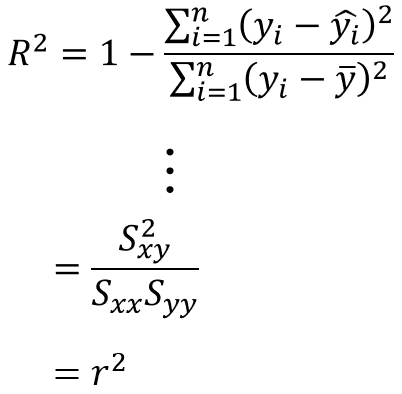
エクセルを使った相関係数の求め方
相関分析のやり方、相関係数の定義が分かったところで、実際にエクセルを使って相関係数を求めてみましょう。
エクセルでは次に示す3つの方法で相関係数を求めることができます。
- 散布図から近似曲線を引く方法
- CORREL関数を使う方法
- アドインを使う方法
散布図から近似曲線を引く方法
データをプロットした散布図に近似曲線を追加することで、グラフ上に近似曲線の数式を出力することができます。
やり方は簡単で、プロットした点の付近にマウスのカーソルを近づけて右クリックすると、次のように「近似曲線の追加」というメニューが表示されます。
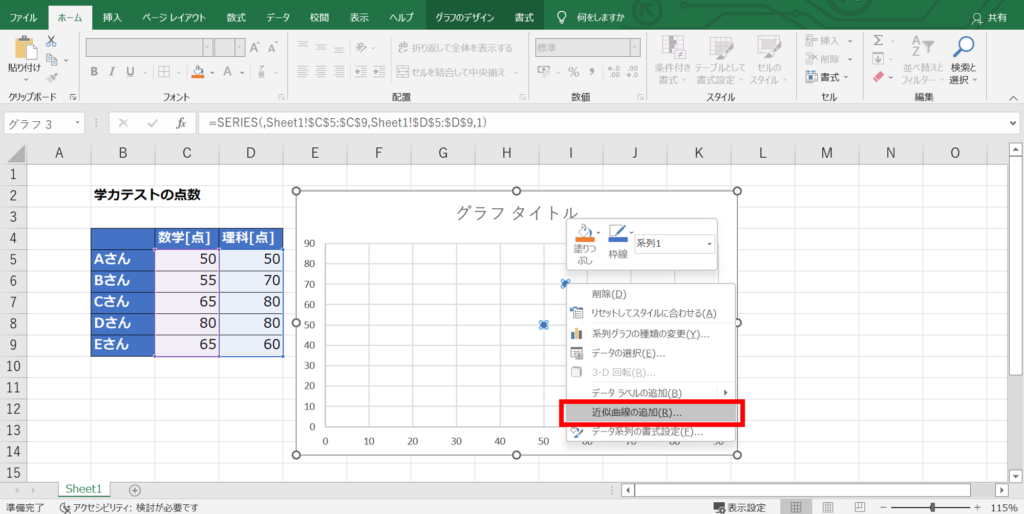
ここで「線形近似」を選択し、「グラフにR-2乗値を表示する」にチェックを入れるとグラフ上に決定係数が表示されます。
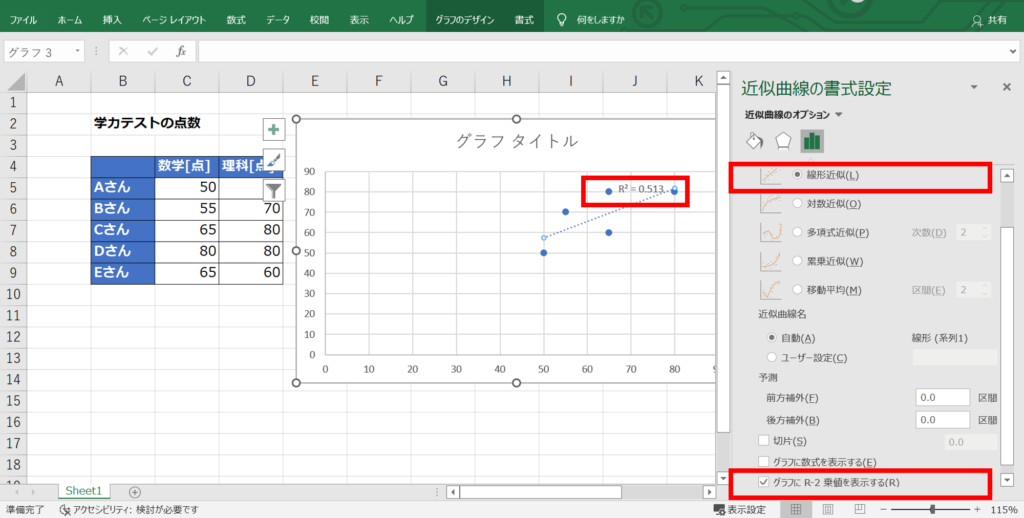
あとは、この平方根を計算すると、相関係数を求めることができます。
CORREL関数を使う方法
次に、関数を用いる方法です。
相関係数を求める際には、CORREL関数を用います。
「数式」⇒「その他の関数」⇒「統計」からCORREL関数を選択するか、セルに直接関数の名前を入力し、相関係数を求めたい2変数のデータを配列1と配列2に入力します。
これは相関行列を求めたい場合など、行と列の参照セルを変えて計算する際に有効で、ぜひ覚えておきたい関数の一つです。
アドインを使う方法
最後にアドイン機能を使う方法です。
アドイン機能が有効になっていない場合は、以下の画面でチェックボックスを入れると有効化できます。
「ファイル」⇒「その他」⇒「オプション」
「アドイン」⇒「分析ツール」にチェックを入れてOKを押す。
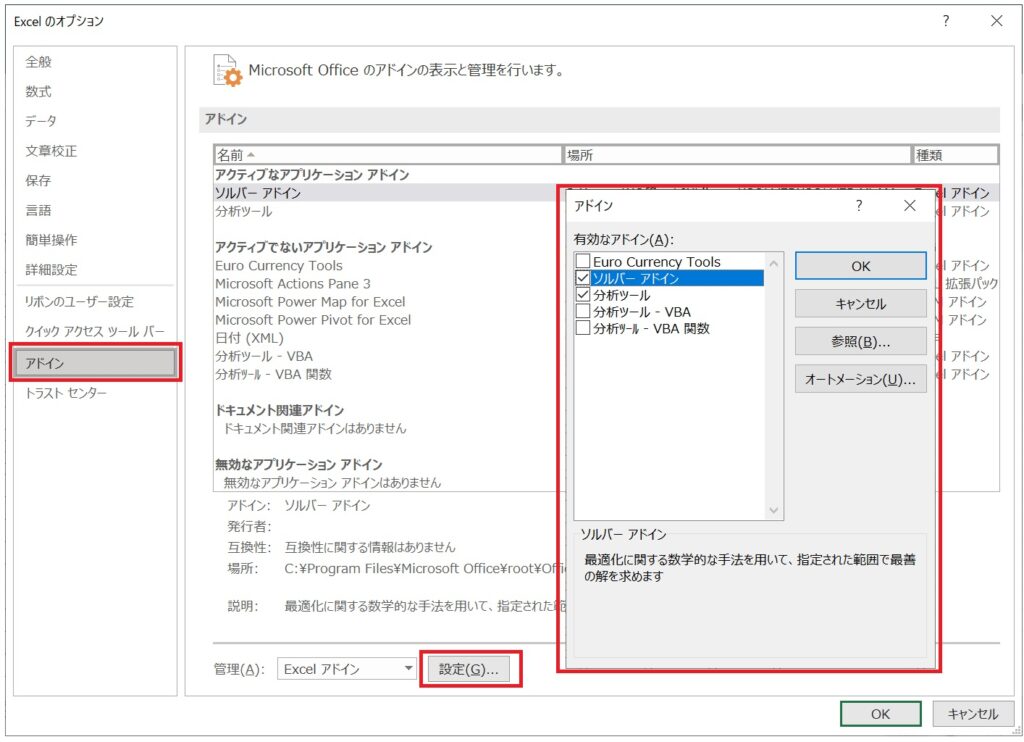
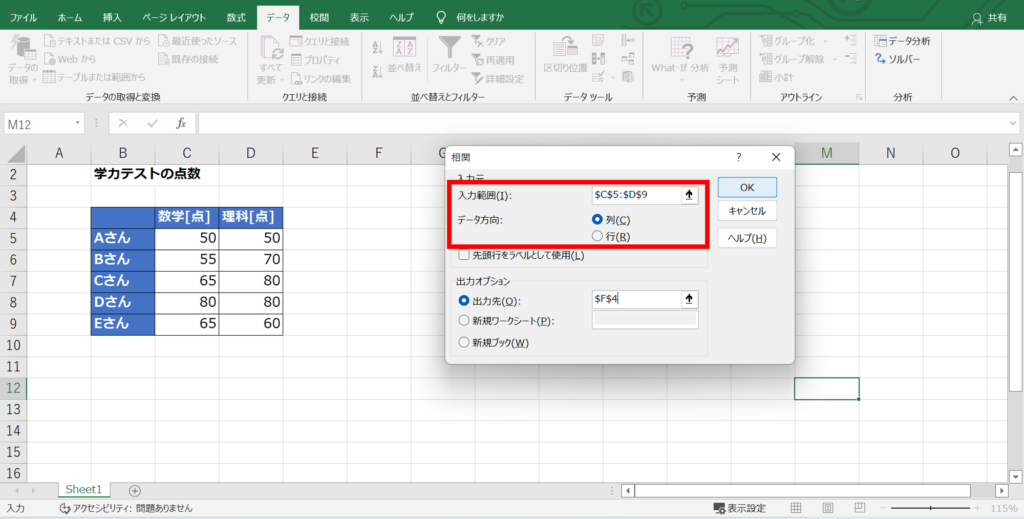
手順としては、「データ」⇒「データ分析」を選択し、「相関」メニューを開きます。
あとは、入力範囲にデータを選択し、データの並び方向として行または列を選択すれば、相関行列を出力することができます。
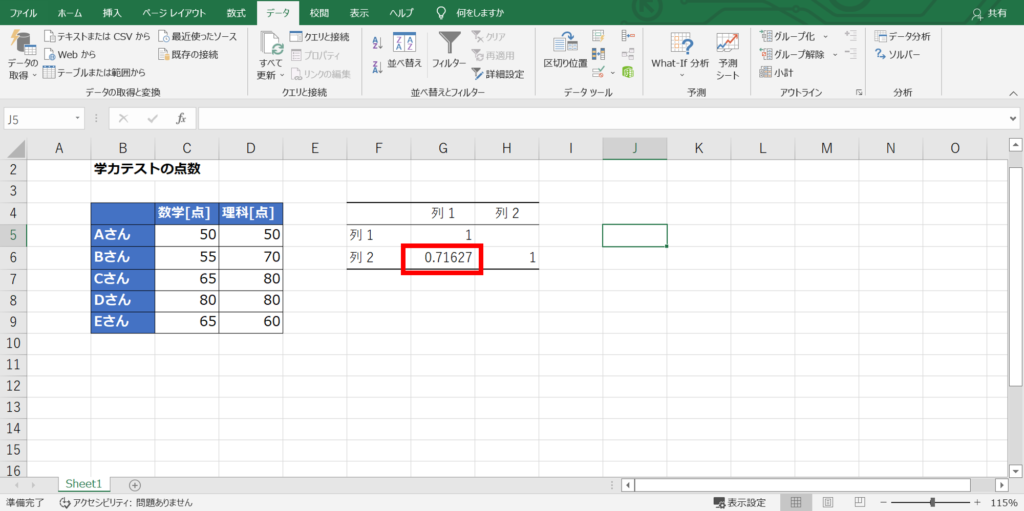
今回の場合、変数が2つの相関行列なので、列1と列2の交差する箇所が求めたい相関係数となります。

場面に応じて選べるように全部覚えておこう
相関分析を行う上での注意点
- 異常点はないか
- 疑似相関がないか
- 層別の必要性はないか
- 外挿は適切か
異常点はないか
次のような異常点が見られる場合は、データが正しく取得できていない、もしくは何らかの前提条件が異なるなど単純比較に適していないデータである可能性が高いです。
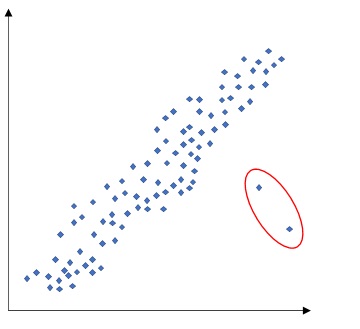
このようなプロットが見られた場合には、データの素性を精査して、必要に応じて除外するなどの処置を取りましょう。
疑似相関がないか
疑似相関(見かけ上の相関、偽相関)とは、実際には因果関係がないのに、別の見えていない要因によって、関連性があるように見える状態です。
よく例に挙げられるのが、「足の大きさと算数のテストの点数」といった関係です。
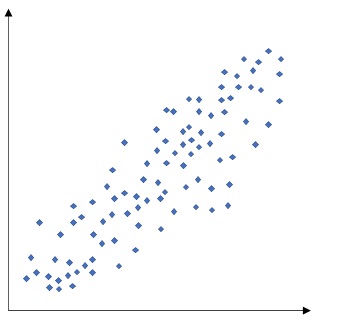
一見、正の相関に見えますが、「足の大きさ」と「テストの点数」に因果関係があるわけではなく、「学年」という要因が抜けているのです。
この散布図を学年で層別してみましょう。
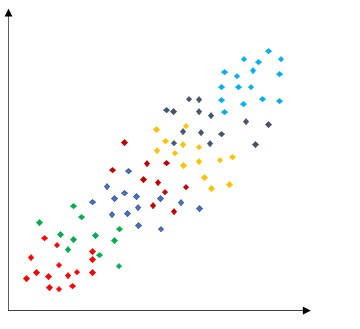
学年ごとに偏りがあり、同じ学年どうしで見てみると全く相関関係はありません。
このように、見えていない要因(潜伏変数)はないか、因果関係がきちんと説明できるか、ということに注意する必要があります。
層別の必要性はないか
上記でも説明した通り、複数の要素に分類(層別)すると、相関を見いだせる場合があります。
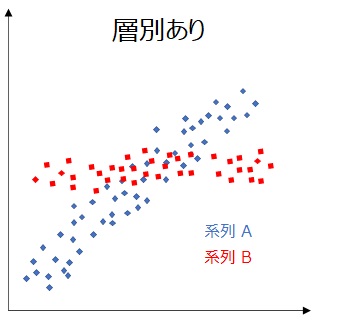
製造業での事例としては、作業者、装置、材料ロット、作業方法などの4Mの要素に着目して分類すると、関係性が見えてくることがあります。
4Mとは、Man(人)、Machine(機械)、Material(材料)、Method(方法)のことで、例えば、特定の装置や作業者で相関が出るような場合は、なんらかの異常や特徴が潜んでいるのかもしれません。
外挿は適切か
外挿とは、範囲外の結果を推定して求めることを表します。
例えば、以下の例では集計データは左下に集中していますが、この状態で近似曲線を引いて範囲外の結果を算出するようなイメージです。
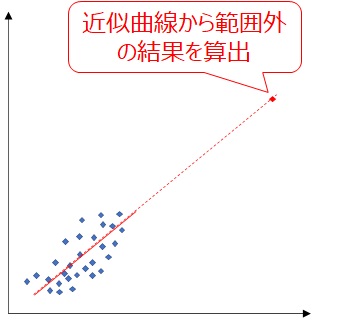
ここで、以下に注意が必要です。
①:集計データの範囲が狭い場合
②:近似曲線の相関精度が低い場合
③:離れすぎた点を外挿で求める場合
外挿する場合、近似曲線の誤差が比例して影響するので、不適切でないか確認しながら実施しましょう。
まとめ
- 相関分析
要因どうし、または要因(原因)と特性(結果)の関係性を統計的かつ定量的に分析する手法のこと。以下の3つの特徴がある。
・変数どうしの因果関係は仮定しない
・取り扱う変数は2つで、一対一で比較する
・変数どうしの直線的な関係の強さを調べる - 目的・メリット
・関係性を見つける
・関係の強さを定量的に表す - 回帰分析との違い
・回帰分析では因果関係を仮定する
・説明変数は2つ以上でも可 - 相関分析のやり方
・散布図から傾向を読み取る方法
・相関係数で定量的に表す方法 - エクセルを使った相関係数の求め方
・散布図から近似曲線を引く方法
・CORREL関数を使う方法
・アドインを使う方法 - 相関分析を行う上での注意点
・異常点はないか
・疑似相関がないか
・層別の必要性はないか
・外挿は適切か
最後までご覧いただきありがとうございました。
まずは相関分析の基本から始めたい方に。
相関分析から単回帰・重回帰分析まで幅広く。
多変量解析マスターを目指すなら。




コメント