「OC曲線から何が分かるの?」
「どのように読めば良いのか分からない」
「自分で計算してOC曲線を作りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
OC曲線(Operating Characteristic Curve)は抜取検査を行う際に、サンプルサイズや合格判定個数の妥当性、ロットの合否判定の見誤りリスクを調べる上で用いられるグラフです。
しかし、ふだん聞きなれない名前から敬遠しがちになり、一体何が分かるのか、そもそもOC曲線をどのように読めば良いのか、お困りではありませんか。
実は、OC曲線は難しい計算も要らず、読み取り方もとても簡単なもので、基本的な項目を一度覚えてしまえば、さまざまな応用にも対応できます。
この記事では、OC曲線の読み取り方と作り方、確率計算の方法、エクセル関数を用いてOC曲線を作成する方法について、初心者のかたにも分かるよう詳しく解説しています。
ぜひ最後まで読んで参考にしていただければ幸いです。
また、YouTubeチャンネルでは、このブログの内容を動画で解説していますので、あわせてご覧いただけると幸いです。
OC曲線とは?
OC曲線は検査特性曲線とも呼ばれ、抜取検査を行う際に、サンプルサイズや合格判定個数の妥当性、ロットの合否判定の見誤りリスクを数値化する上で活躍するグラフです。
抜取検査は、全数検査と比べて検査にかかるコストを抑制でき、さらに破壊試験も適用できる利点があります。
その一方で、確率計算に基づいてロットの合格/不合格を判定する性質から、本来は不合格とすべき品質の悪いロットを合格と判定して出荷してしまう見逃しリスクが伴います。
また反対に、本来は合格とすべきロットを不合格にして出荷を取りやめるケースもあり、この場合は生産者側のリスクとして織り込んでおかねばなりません。
では、具体的にどの程度の割合で判定を見誤るリスクがあるのかというと、ここで登場するのがOC曲線です。

リスクの大きさは定量的に考えよう
とあるロットからサンプルを抜き取って、不適合品の個数でロットの合否を判定する検査を計数規準型抜取検査と呼びます。
一方、サンプルから計量値を測定して平均値や標準偏差を求め、合格判定値と数値で比較する検査のことを計量規準型抜取検査と呼びます。
計数規準型抜取検査では、サンプルサイズや合格判定個数によって見誤るリスクの大きさが変わるので、妥当な検査規準を設計する上で重要な役割を担っています。
以降で記載する抜取検査は、計数規準型抜取検査のこととして、まずは、OC曲線の構成と読み取り方から解説していきます。
OC曲線の読み方
OC曲線のグラフの構成
早速、OC曲線の代表例を用いて、グラフの構成を見てみましょう。
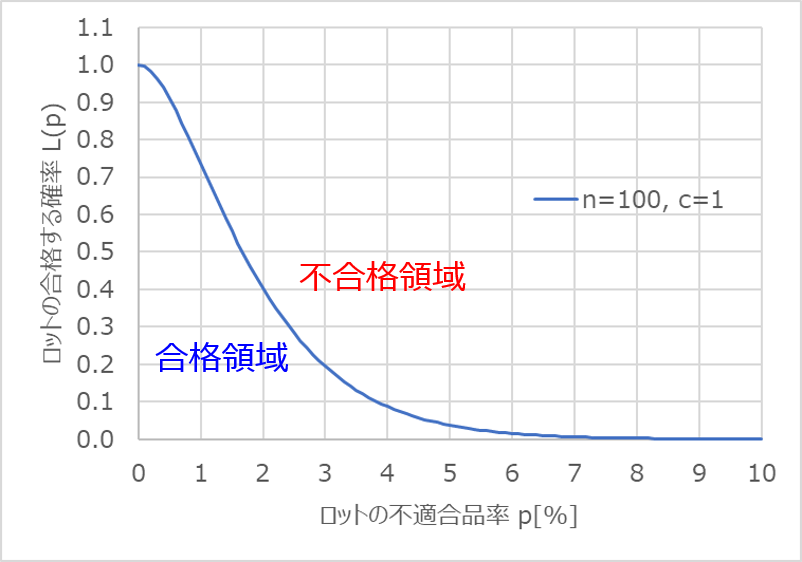
横軸にはロットの不適合品率$p$(不良率)をパーセント表記で、縦軸にはそのロットが合格と判定される確率$L(p)$を取ります。
計算のしかたは後述しますが、$p$に対応する$L(p)$の値を求め、各点をプロットするとOC曲線が得られます。
サンプルサイズや合格判定個数によって、多少はカーブの形状が変わったり、左右にシフトしたりしますが、$p=0$で$L(p)=1.0$となり、途中で変曲点を持つ形状は共通しています。
$n$はサンプルサイズ、$c$は合格判定個数を表します。
つまり、ロットから$n$個のサンプルを抜き取って、不適合品(不良品)の個数が$c$個以下であればそのロットは合格、$c+1$個以上であれば不合格と判定します。
ロットが合格となる確率
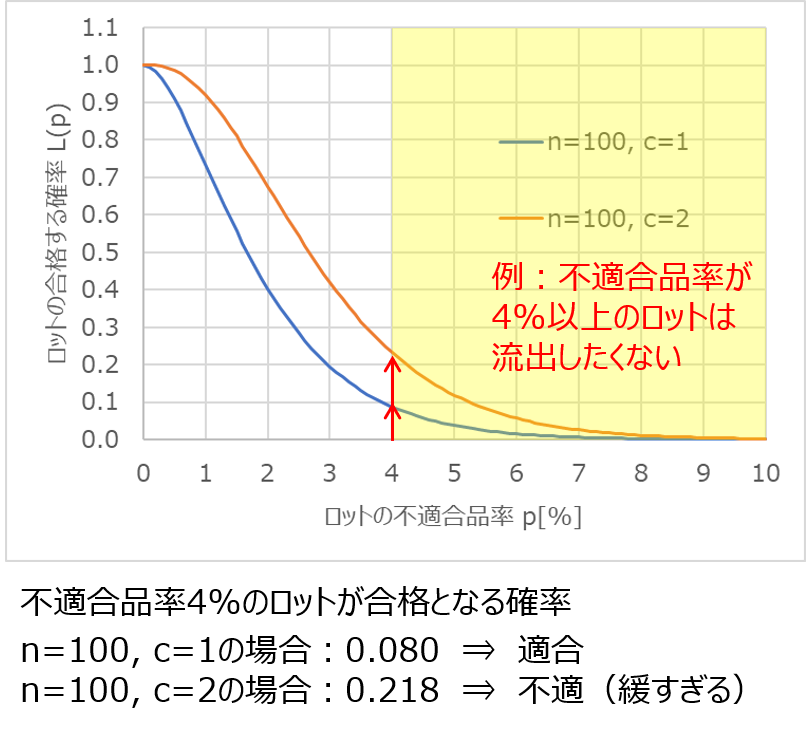
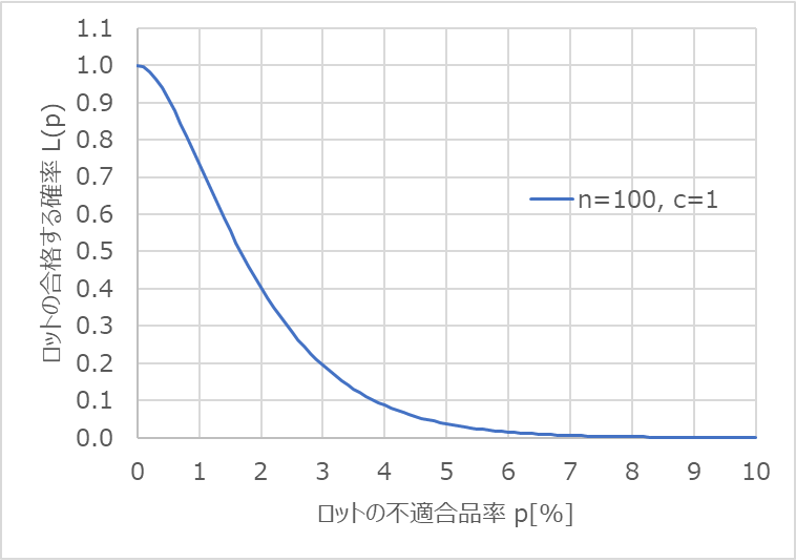
以下は、$n=100$、$c=1$のOC曲線です。
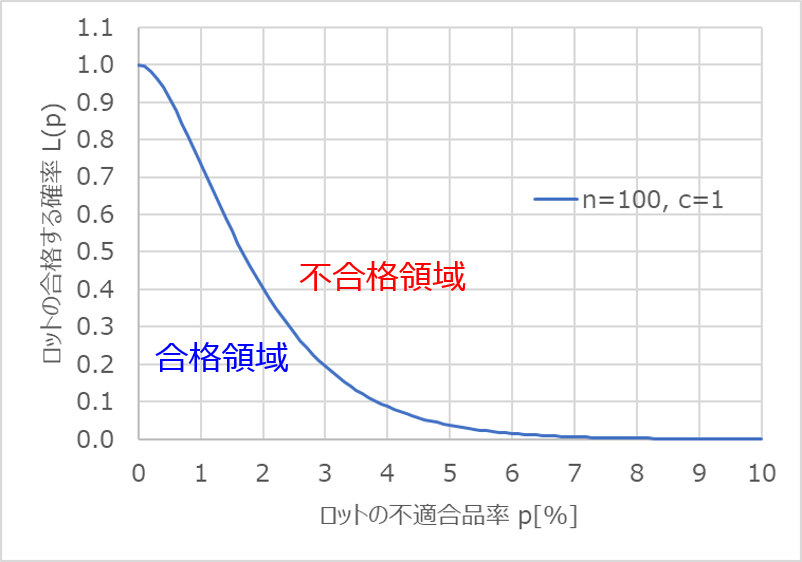
例えば$p=1$%、つまり100個に1個の割合で不適合品が出るロットに着目すると、この時の$L(p)$の値は0.736と読み取れます。
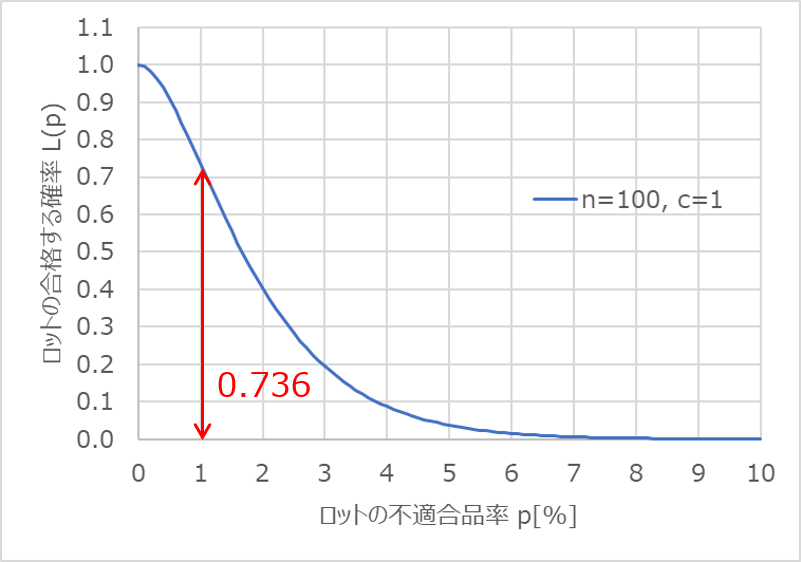
すなわち、不適合品率1%のロットにおいて、100個の抜取検査を行い、不適合品が1個以下であれば合格とする場合、このロットが合格する確率は0.736(73.6%)というわけです。
ここで、消費者危険について考えてみましょう。
消費者危険とは、本来は不合格とすべき悪いロットを合格と判定して出荷してしまう「見逃しリスク」のことを意味し、第2種の誤りとも呼ばれます。
通常、消費者危険をいくつに設定するか、あらかじめ客先が決まっている場合には合意を得てから抜取検査のサンプルサイズと合格判定個数を決めることも多くあります。
消費者危険は$β$の記号で表され、一般的に0.10(10%)と設定するケースが多いです。
ここで、$L(p)=0.1$となる$p$の値を読み取ると、約3.9%となります。
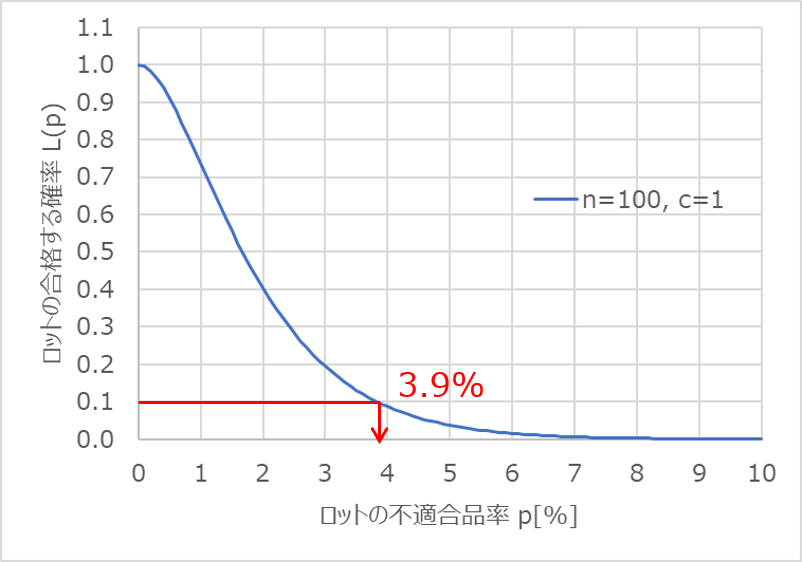
つまり、ロットの不適合品率が3.9%以上であれば、100個に1個の抜取検査で誤って悪いロットを出荷してしまう確率$β$を0.1(10%)以下に抑えられるということです。
元々のロットの不適合品率の値が大きいほど、抜取検査での見逃しリスクが減るのは直感的にも理解いただけると思います。
なお、抜取検査を設計する順序としては、消費者危険$β$を0.1以下にするための不適合品率の下限値$p1$をあらかじめ設定し、これを満足する$n$と$c$の値を決める流れになります。
ロットが不合格となる確率
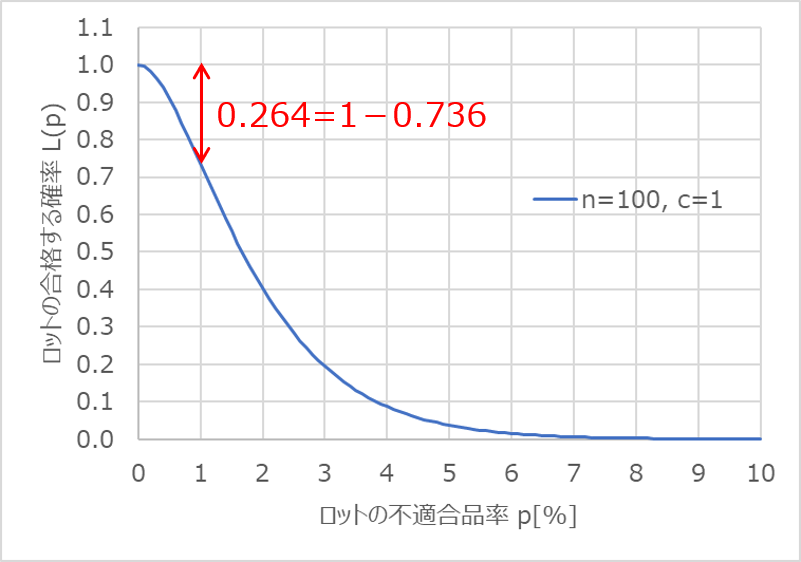
続いて、ロットが不合格となる確率を見てみましょう。
考え方は単純で、合格する確率の反対が不合格となる確率です。
先ほどのOC曲線を例にすると、$p=1$%における$L(p)$の値は0.736ですので、反対に不合格となる確率は0.264(26.4%)となります。
誤って不合格としてしまう場合には、今度は生産者側が損をすることになります。
生産者危険とは、本来は合格とすべき良いロットを不合格と判定して出荷を取りやめる「見過ぎリスク」を意味し、第1種の誤りとも呼ばれます。
生産者危険は$α$の記号で表され、一般的に0.05(5%)と設定するケースが多いです。
ここで、$L(p)=0.95$となる$p$の値を読み取ると、約0.4%となります。
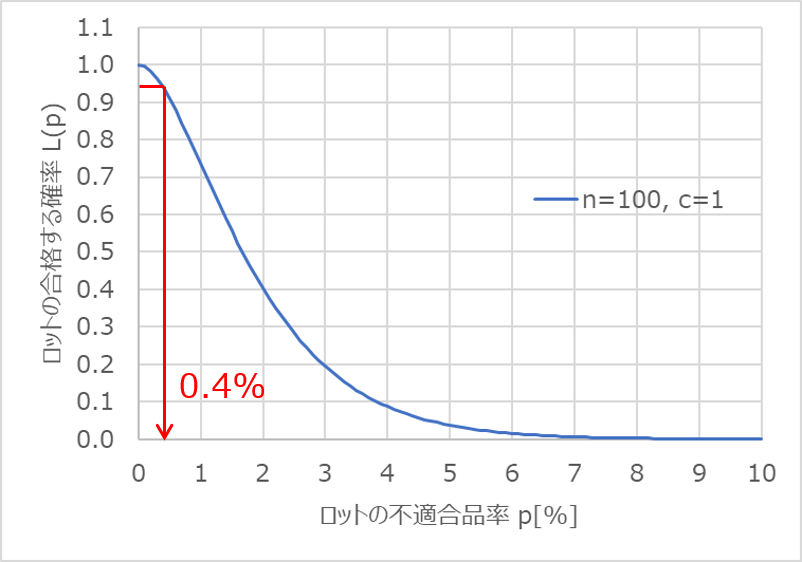
つまり、ロットの不適合品率が0.4%以下であれば、100個に1個の抜取検査で誤って良いロットを廃却してしまう確率$α$を0.05(5%)以下に抑えられるということです。
なお、消費者危険と同様に、生産者危険$α$に関しても不適合品率の上限値$p0$をあらかじめ設定してから、$n$と$c$の値を決めます。
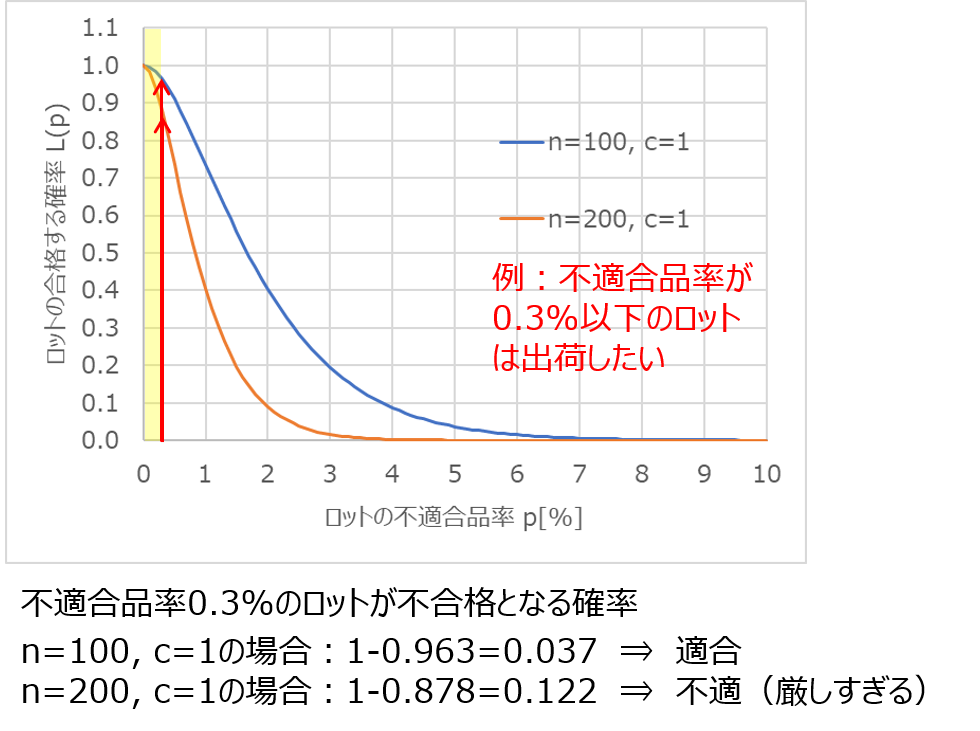
そのため、生産者危険と消費者危険の両方のバランスが取れる$n$と$c$の値を決める必要があるのです。
計数規準型抜取検査ではJIS規格で対応表が掲載されており、これを用いると簡単に$n$と$c$の値を決めることができます。
対応表の読み取り方は、個別の記事で解説していますので、合わせてご覧ください。

OC曲線の作り方
ここまででOC曲線の読み取り方が理解できたところで、次は自分でOC曲線を作ってみましょう。
先ほども説明した通り、抜取検査の設計手順としては次のようになります。
- 客先と合意の上で$α$と$β$を決める
- $α$と$β$の目標値に対応する不適合品率の上限値$p0$と下限値$p1$を設定する
- JIS規格の対応表を用いて、$α, β, p0, p1$に対応する$n$と$c$の値を決める
サンプルサイズ$n$と合格判定個数$c$が決まると、あとはロットの不適合品率$p$に対応するロットが合格する確率$L(p)$を計算します。
計算のしかたには、次の3つの方法があります。
それぞれ計算結果の違いと合わせて比べてみましょう。
二項分布から求める方法
母集団からサンプルを取って、合格/不合格を判定すると言えば、真っ先に思い当たるのが二項分布ではないでしょうか。
名前は聞いたことのある方が多いと思いますが、確率$p$で起こる事象に対して、$n$個の集団から$k$個を抜き取る場合、以下の式で発生確率を求められます。
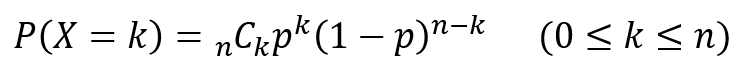
これを抜取検査に当てはめると、数式の$k$を合格判定個数$c$に置き換えることになります。
ここで注意が必要なのが、二項分布は「復元」を前提としたサンプリングであることです。
復元とは、一度抜き取ったものを元の集団に戻すことを意味し、反対に戻さない場合を非復元と呼びます。
実際の抜取検査ではサンプリングは非復元であるため、厳密には二項分布ではなく、後ほど説明する超幾何分布を用いるのが正しいです。
ただし、母集団の数$N$に対するサンプルサイズ$n$の比が十分に大きい場合、具体的には$N/n$が10以上の場合、超幾何分布は二項分布に近似できるのです。
二項分布と比べて、超幾何分布は計算が非常に複雑になるので、近似できる場合には二項分布を用いると良いでしょう。
今回の事例では、サンプルサイズ$n=100$、合格判定個数$c=1$であり、例えば$p=1$%における$L(p)$の値は次のように求められます。
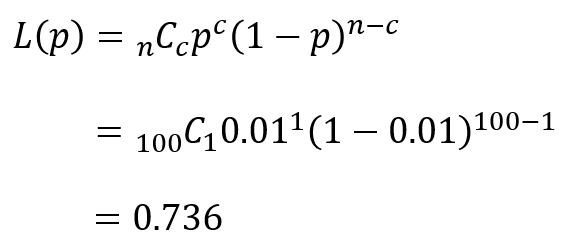
同様にいくつかの$p$の値に対して$L(p)$を求め、プロットした点をつなげば、OC曲線を描くことができます。
なお、二項分布に関しては以下の記事で詳しく解説していますので、合わせてご覧ください。

超幾何分布から求める方法
超幾何分布は「非復元」を前提とした確率分布で、次の式から発生確率を求められます。
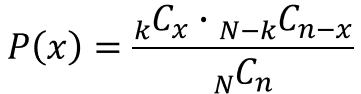
$N$は母集団の数、$k$は母集団のうち片方の群(例えば不適合品)の数、$n$はサンプルサイズ、$x$は$n$個のサンプルの中に含まれる片方の群(不適合品)の数を表します。
今回、$N$を1000個、$k$を10個(不適合品率1%)とします。
サンプルサイズ$n$は100個、$x$は合格判定個数$c$のことで1個になります。
先ほどの式に当てはめて計算すると、次のようになります。
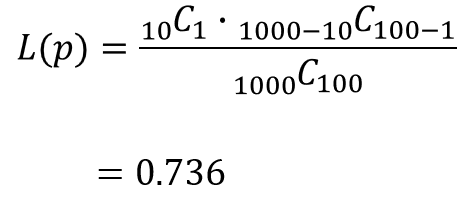
二項分布の結果と比べると、小数点3桁まで同じであり、二項分布でも十分に精度のある計算ができていることが分かります。
ちなみに、ここではエクセルを用いてHYPGEOM.DIST関数を用いて計算しましたが、これを電卓でやろうとすると途方もない労力がかかります。
そのため、真っ向から超幾何分布で計算するのではなく、できるだけ二項分布で近似する方が望ましいのです。

確かに1000C100って、どうやって計算するんだ?
なお、超幾何分布に関しては以下の記事で詳しく解説していますので、合わせてご覧ください。

累積確率曲線から求める方法
3つ目の手法としては、累積確率曲線(ソーンダイク-芳賀曲線)を用いて値を読み取るというものです。
累積確率とは、その名の通り確率を累積したもので、例えば合格判定個数をゼロから$c$まで累積した確率を曲線にしたものも累積確率曲線の一つです。
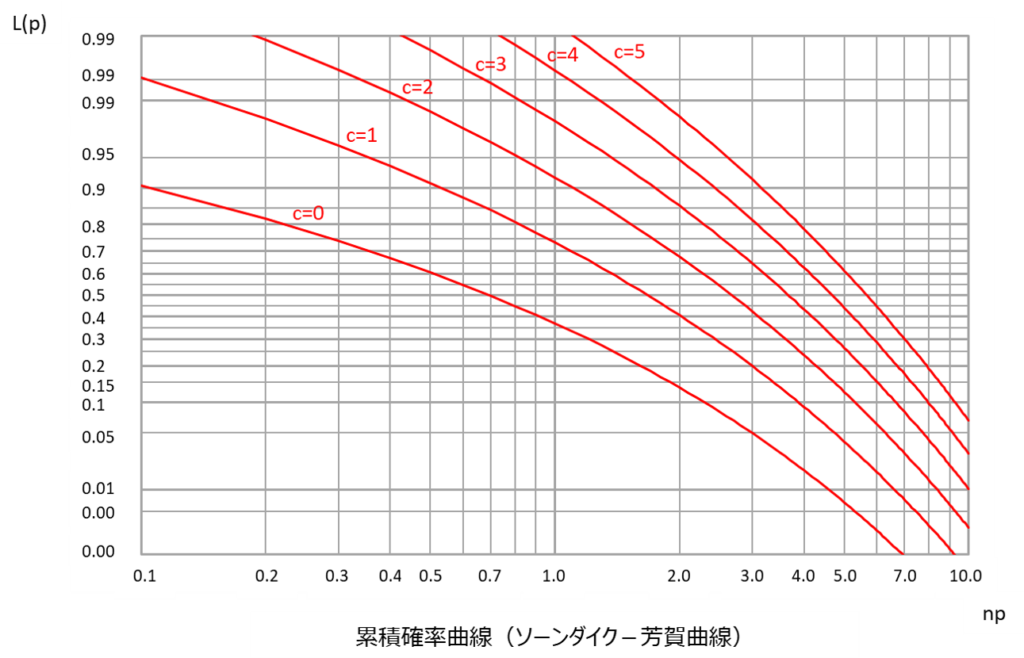
横軸には$n$と$p$を掛け算した$np$を取り、縦軸には$L(p)$を取ります。
そして、$c$の値ごとに系列を分けた曲線が描かれています。
つまり、あらかじめ合格判定個数ごとに求められた発生確率が曲線としてプロットされており、単に$np$の値に該当する$L(p)$を読み取れば良いという便利なものなのです。
先ほどの例でいうと、$np$の値は1(100×0.01)となり、この時の$L(p)$の値は0.736となります。
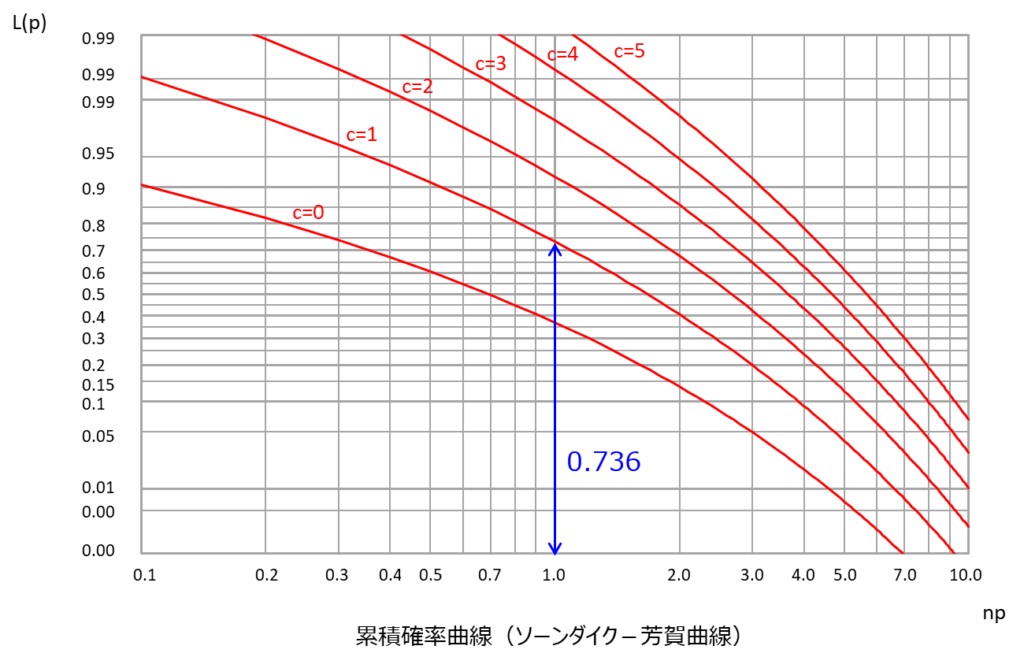
まさに、二項分布、超幾何分布で求めた答えとぴったり合致しますね。
なお、ソーンダイク-芳賀曲線はポアソン分布を元に確率を計算しています。
ポアソン分布は以下の式で定義される確率分布で、$λ=np$、$k=c$と置き換えると、$c$の値ごとに発生確率を求めることができます。
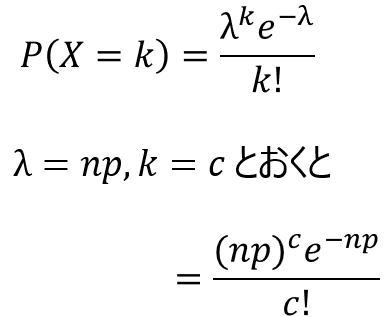
そして、$k$に対して$0~c$までを累積すれば、累積確率$L(p)$を求めることができるのです。
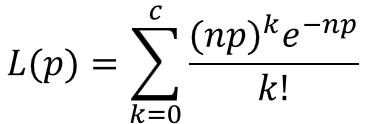
なお、二項分布において、$n$が十分大きく、$p$が十分小さい場合($np≦5$)、すなわち発生する事象が稀なものとみなせる場合において、ポアソン分布に近似できる関係性があります。
抜取検査における不適合率も稀な事象に該当し、二項分布の計算をポアソン分布で近似して行っているわけです。
ポアソン分布については、以下の記事で詳しく解説していますので、合わせてご覧ください。

ここまで、二項分布、超幾何分布、ポアソン分布のそれぞれの求め方で結果を比較しましたが、結局どの手法で計算してもほとんど違いがないことが分かっていただけたと思います。
ソーンダイク-芳賀曲線が手元に準備できる場合は、単純にグラフを読み取るだけなので最も手軽ですが、ない場合は二項分布を用いて計算するのが良いでしょう。
エクセルでの作り方
さて、計算方法まで理解できたところで、あとはグラフにするだけです。
エクセルを使う場合には、二項分布の計算も含めて便利な関数があるので、手軽にOC曲線を作成することができます。
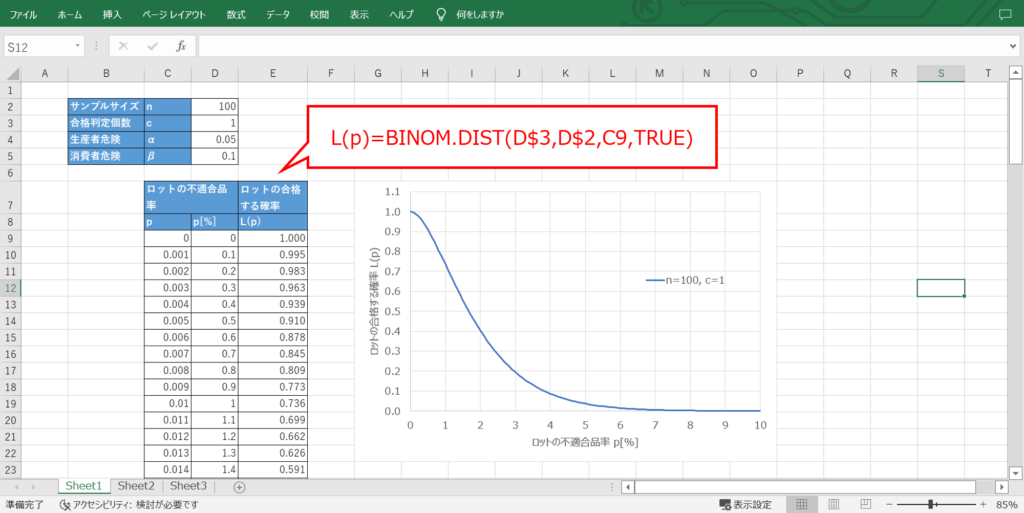
二項分布の確率を返す関数として、BINOM.DIST関数があります。
二項分布は英語でbinomial distributionと呼ぶので、BINOMはこれの頭文字を取ったものです。
使い方は簡単で、次の4つの変数を指定するだけです。
①:成功数(c)
②:試行回数(n)
③:成功率(p)
④:関数形式(TRUE or FALSE)
④の関数形式については、確率質量関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを使うので、今回の場合はTRUEを用います。
この関数を用いて、$p$の値ごとに発生確率を計算すれば、あとはデータ範囲を指定してグラフにすると完成です。
OC曲線の変化をシミュレーション
エクセルを用いるメリットとして、$n, c, p$の変数の値を変えたときの再計算が瞬時にできることです。
例えば、合格判定個数を緩くしたらOC曲線がどう変化するのか、$n$と$c$の比率は同じでサンプルサイズを増やしたらどうなるのか、簡単に見積ることができます。
品質管理検定(QC検定)でも頻出の問題なので、ぜひ一度ご自身で試してみてください。
合格判定個数cの値を変えた場合
次のグラフは、$c$を1~3まで変えたときのOC曲線です。
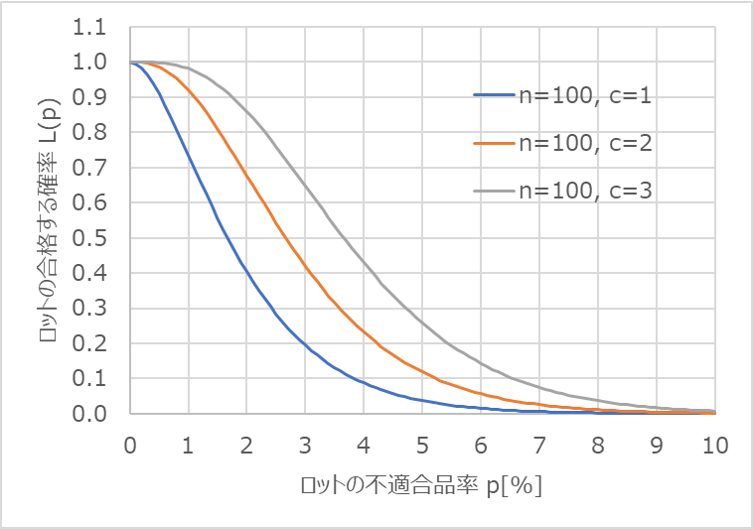
合格判定個数$c$が増えるにつれて、グラフが右側にシフトしていることが分かります。
$c$を増やすというのは判定を緩くすると同義で、すなわち生産者危険や消費者危険も今までと同じレベルを維持するのに、不適合品率が従来よりも高くなって良いことを意味します。
nとcの比率は同じでサンプルサイズを増やした場合
次のグラフは、$n$と$c$の比率を固定して、サンプルサイズを増やした場合のOC曲線です。
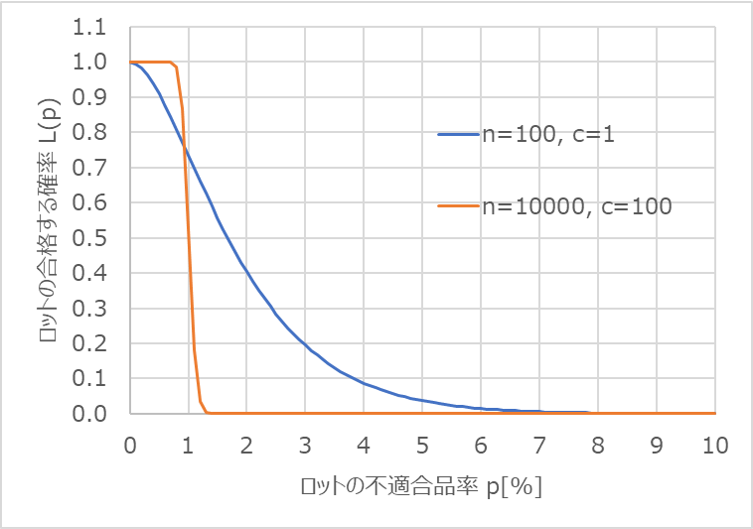
なだらかであった曲線が急峻になり、変曲点を境に左側は確率が高く、右側は確率が低く変化しています。
この時の生産者危険($α=0.05$)と消費者危険($β=0.10$)に対応する$p0$と$p1$の限界値を求めると次のようになります。
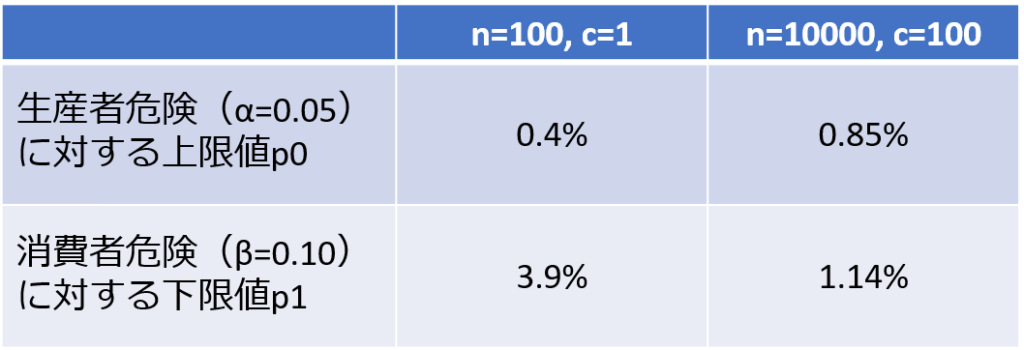
サンプルサイズを増やしたことで、$p0$の上限値は0.85%、$p1$の下限値は1.14%となり、それぞれ変曲点の確率$p$に近づいたことが分かります。
これは、ロットの合否を分類する判定の精度が高くなっていることを意味します。
サンプルサイズを大きくして母集団から抜き取る数を増やしているので、精度が上がるのは納得できることですね。

検査が厳しくなるのか緩くなるのか、感覚と一緒に覚えておこう
なお、ロットの合否を100%間違いなく分類できる場合、OC曲線は以下のようになります。
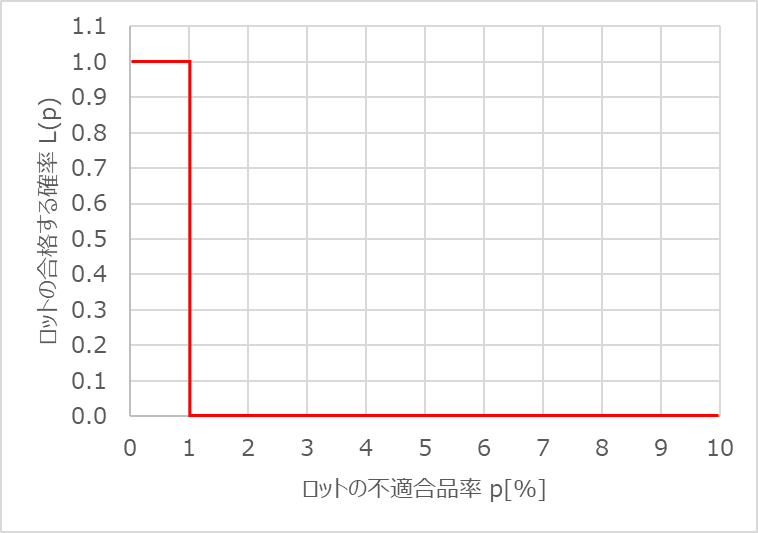
不適合品の確率1%を境に合格率100%から0%に変化しています。
この1%という境界の値は、母集団の不適合品率のことであり、合否を誤りなく確実に判定できる全数検査のことを表しているのです。
まとめ
- OC曲線(検査特性曲線)
サンプルサイズや合格判定個数の妥当性、ロットの合否判定の見誤りリスクを調べるための確率グラフ
横軸:ロットの不適合品率$p$(不良率)
縦軸:合格と判定される確率$L(p)$ - 消費者危険
本来は不合格とすべき悪いロットを合格と判定して出荷してしまう「見逃しリスク」のことで、第2種の誤りとも呼ぶ - 生産者危険
本来は合格とすべき良いロットを不合格と判定して出荷を取りやめる「見過ぎリスク」のことで、第1種の誤りとも呼ぶ - $L(p)$の確率の計算方法
二項分布を用いて計算する方法
超幾何分布を用いて計算する方法
ソーンダイク-芳賀曲線(ポアソン分布)を読み取る方法 - エクセルで計算する方法
二項分布の確率を返すBINOM.DIST関数を用いる - パラメータを変えた場合のOC曲線の変化
①:合格判定個数$c$の値を変えた場合
⇒$c$を減らす(厳しくする)と左側、増やす(緩くする)と右側にシフト
②:$n$と$c$の比率固定でサンプルサイズを増やした場合
⇒変曲点を基点に傾きが急峻になる(合否判定の精度が上がる)
最後までご覧いただきありがとうございました。
抜取検査のエッセンスが詰まった本はズバリこれ
QC検定2級対策として、計数規準型抜取検査、計量規準型抜取検査を効率よく学習したい方はこちら
QC検定1級対策として、選別型抜取検査、調整型抜取検査を効率よく学習したい方はこちら




コメント