「超幾何分布ってどのような分布なの?」
「期待値と分散の計算の仕方を知りたい」
「エクセルでグラフ化したい」
このような疑問や悩みをお持ちの方に向けた記事です。
超幾何分布とは、2つの性質で構成される集団から非復元でサンプルを採取した場合において、対象とする性質のものがいくつあるかという確率を表す離散型の確率分布です。
例えば、赤玉と白玉が入った袋から非復元で△△個の玉を取り出す場合に、取り出したサンプルのうち赤玉が○○個となる確率が超幾何分布に該当します。
ちなみに、非復元とは、一度採取したサンプルを元の集団に戻さないことを意味します。
この記事では、超幾何分布の定義、二項分布との関係、期待値と分散の導出の仕方、エクセルでグラフ化する手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
超幾何分布とは?
例えば、袋の中にN個の玉が入っていて、そのうち赤玉がk個、白玉がN-k個入っているとします。
この袋からn個の玉を取り出した場合に赤玉がx個とすると、その確率は以下の超幾何分布の数式に従います。
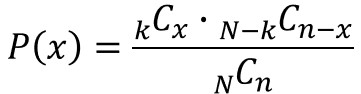
分母の項は、N個からn個を取り出す場合の通り数を表します。
分子の項は、k個の赤玉からx個を取り出す通り数、及びN-k個の白玉からn-x個を取り出す通り数を掛け合わせたもので、すなわち赤玉がx個となる全通り数を意味します。

意味が分かれば数式も覚えやすいね
超幾何分布における確率変数Xは、個数や回数を表す変数であり、1個、2個・・と数えることのできる計数値です。
そのため、例えば1から2の間の小数点以下の変数は取らない、離散的な変化をする性質の確率分布となっています。
このような離散型の確率分布が示す確率のことを確率質量関数と呼び、P(X=k)として表されます。
離散型確率分布や確率質量関数ついては、別の記事で詳しく解説していますので、合わせて参考にしていただければと思います。

二項分布との関係
超幾何分布と性質の近い分布として、二項分布があります。
二項分布とは、成功か失敗のいずれかで表される試行(ベルヌーイ試行)を何回も繰り返した場合における成功回数の分布を表し、以下の数式で定義されます。
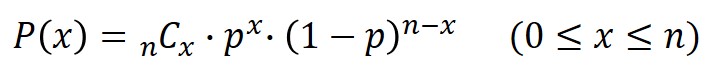
pは成功確率、kは成功回数、nは試行回数を表します。
2つの性質で分類される点や、その試行を何度も繰り返す点など、何となく似ているように思いませんか?
実は両者は似て非なるもので、二項分布が常に発生確率が一定となる「復元の抽出」であることに対し、超幾何分布では抽出するごとに確率が変化する「非復元の抽出」となることが特徴です。
先ほどの赤玉と白玉の例を挙げると、最初の一個を取り出す際の赤玉の出る確率は、k/Nとなりますが、二つ目を取り出す際は最初の一個を差し引いて考えなければなりません。
そして、これを一つずつ考えていると、通り数が膨大になって理解が追い付かなくなるので、超幾何分布の数式に当てはめて機械的に確率を求めるというわけなのです。
ちなみに、超幾何分布の数式においてNを無限大にすると、二項分布の式に収束します。
以下に導出の過程を記載しますので、興味のある方は見てみてください。


Nが十分大きいってことは「復元」と同じ意味なんだね

期待値と分散の導出
超幾何分布における期待値E(X)と分散V(X)は、以下の数式で求めることができます。
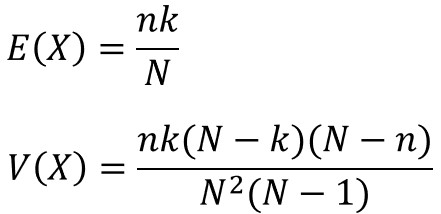
少し難しいですが、導出過程に興味のある方は参考にどうぞ。




二項分布の期待値npと同じになるんだね
なお、E(X)とV(X)の意味、V(X)の導出の過程については、別の記事で解説していますので、合わせてご覧ください。

エクセルでのグラフの書き方
エクセルでの超幾何分布の確率の求め方、グラフの書き方を紹介します。
HYPGEOM.DIST関数を用いれば、確率質量関数を計算することができます。
何とも複雑な文字列で覚えにくそうですが、超幾何の英語hyper geometricの略と、分布distributionの略を繋げた名前が関数名になっています。
使い方は簡単で、次の5つの変数を指定するだけです。
①:標本の成功数(x)
②:標本数(n)
③:母集団の成功数(k)
④:母集団の大きさ(N)
⑤:関数形式(TRUE or FALSE)
ここでは成功数と表現されていますが、赤玉や白玉のように2つの性質に分類されるものを成功と失敗と置き換えて考えてください。
⑤の関数形式については、確率質量関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
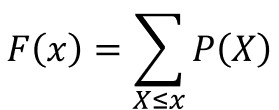
例えば、N=100、k=40、n=20として、確率質量関数P(x)を求めると以下のようになります。
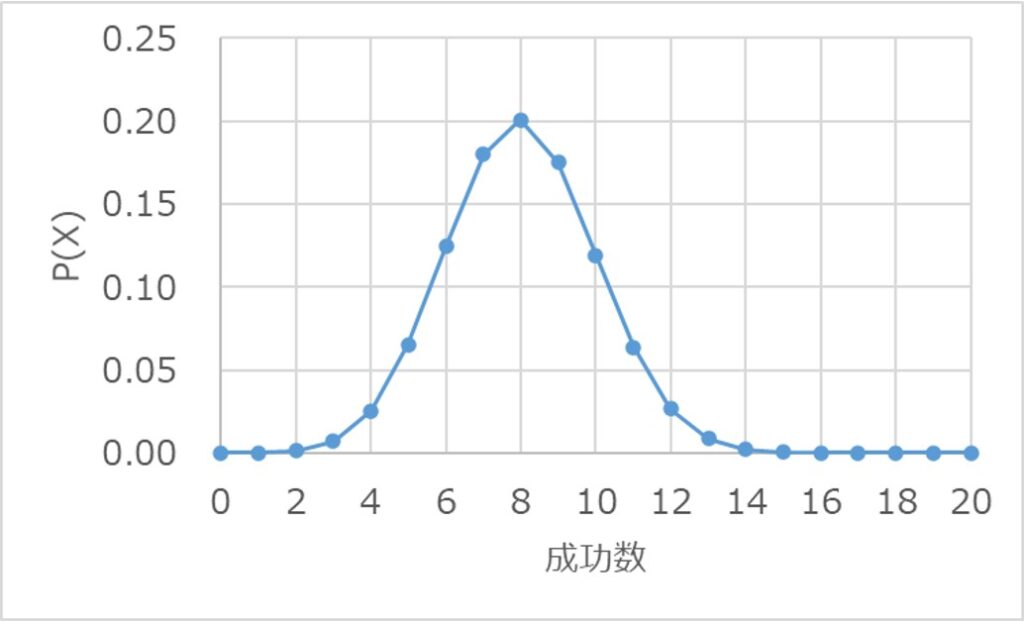
また、同様に累積分布関数F(x)を求めると以下になります。
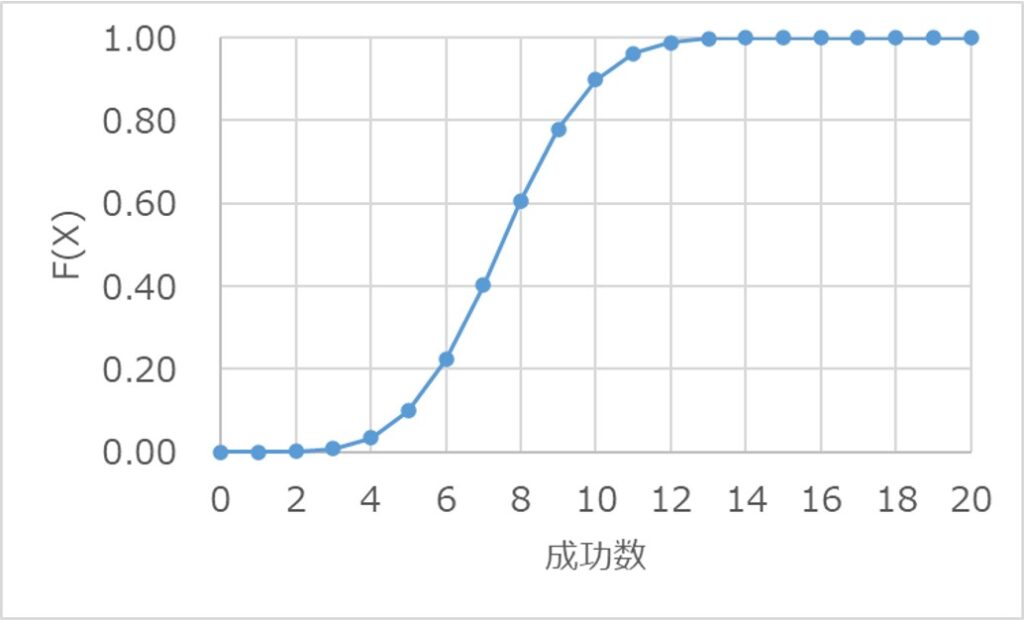
累積分布関数は、確率変数xの値が大きくなるにつれて、1に収束することが見て取れます。
これは、確率の合計値が1になることを表しており、この性質がグラフからも分かります。

例題
まとめ
- 超幾何分布
⇒2つの性質で構成される集団から非復元でサンプルを採取した場合において、対象とする性質のものがいくつあるかという確率を表す離散型の確率分布 - 二項分布との違い
⇒二項分布:常に発生確率が一定となる「復元の抽出」
⇒超幾何分布:抽出するごとに確率が変化する「非復元の抽出」
⇒超幾何分布において、Nを無限大に取ると二項分布になる - 期待値
⇒nk/N - 分散
⇒nk(N-k)(N-n)/N2(N-1) - エクセルでの求め方
⇒HYPGEOM.DIST関数で、確率質量関数と累積分布関数を計算できる
袋から赤玉、白玉を取り出す単純な行為ですが、取り出した玉を戻さないという「非復元」の前提を加えるだけで、確率が一定でなくなり、一挙に考え方が難しくなります。
このような場合においても超幾何分布の計算方法を理解しておけば、エクセルで簡単に求めることができるので、ぜひ使えるようにしておきましょう。
最後まで読んでいただき、ありがとうございました。
この記事で紹介した超幾何分布は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。







コメント