この記事では、1つの母分散に関する統計的検定について記載していますので、参考なればうれしいです。
母分散の検定は、この記事で完結して解説していますが、統計的検定の概念とメリット、登場する用語の意味など、統計的検定(その1)の記事から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

カイ二乗分布とは?
定義
母分散の検定を行うには、カイ二乗分布を使います。
まず、早速登場した「カイ二乗分布」という用語、名前を聞くだけで敬遠したくなりますよね・・。
検定を行うのに細かい数式を覚える必要はないので、ここではカイ二乗分布の概念だけ覚えておいてください。
「カイ」は記号で「$χ$」と表され、以下の数式によって定義されます。
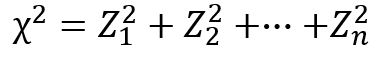
ここで、$Z_{1}~Z_{n}$は標準正規分布に従う互いに独立な確率変数を表します。
標準正規分布とは、正規分布において平均値$μ$を0、標準偏差$σ$を1として基準化したもので、$N(μ,σ^{2})$は$N(0,1)$と表記されます。
この$χ^{2}$が従う確率分布のことをカイ二乗分布と呼び、自由度$n-1$のカイ二乗分布に従うと表現されるのです。
確率変数の二乗和が従う分布なので、すなわち、「ばらつき」「分散」に関わる確率を求める場合に活用されます。
母分散の検定のほかに、独立性の検定や適合度の検定など、同じく分散を扱う検定にも用いられます。
カイ二乗分布のグラフの特徴
カイ二乗分布のグラフは左右対称ではなく、右側に裾広がりの形状を示します。
以下のグラフは、自由度の違いによる確率密度関数の形状の違いを表したものです。
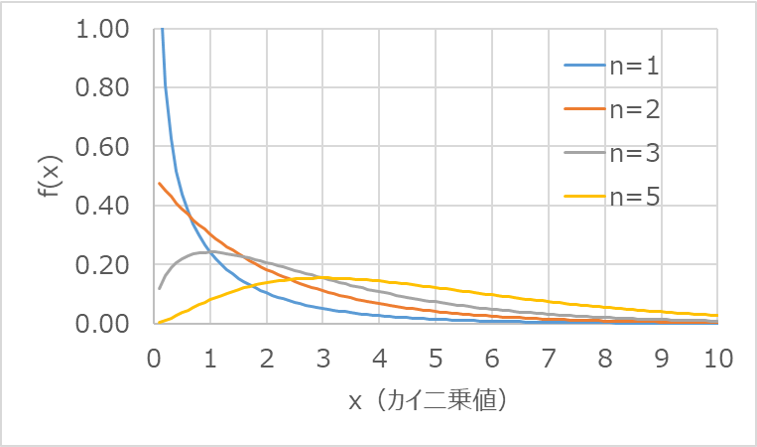
いずれも、右側に広がった分布を示していることが分かります。
二乗和を扱う統計量の分布なので、特に自由度が小さい場合に偏った形状が顕著に表れます。
ここまで説明したカイ二乗分布について、以下の記事で期待値や分散、エクセルでのグラフの書き方を詳しく解説していますので、合わせてご覧ください。

また統計的検定では、区間推定と似た考え方を用いており、検定統計量の計算式も区間推定で登場した式と近いものが多いので、検定と推定はセットで覚えておくとよいです。
母分散の区間推定については、以下の記事で詳しく解説していますので、合わせてご覧いただければと思います。

母分散の検定
早速、具体的な題材を用いて、実際にやってみましょう。
とある工場で作る加工部品に関して、強度のばらつきの大きいことが問題になっており、製造工程を改善してばらつきを抑える対処を施しました。母分散が5より小さければ、この改善策を恒久的に採用したいと思います。改善後の試作品20個の不偏分散が2.6であったとき、この製品の強度ばらつきは目標値よりも小さくなったと言えるでしょうか?
検定統計量
カイ二乗分布では、分布の横軸(カイ二乗値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのCHISQ.DIST関数やカイ二乗分布表で簡単に求められます。
そして、このカイ二乗値を検定統計量として用いることで、母分散に対する検定を行うことができるのです。
検定統計量の計算式は、以下のように表されます。
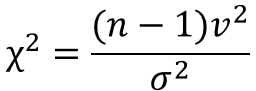
$σ^{2}$は母分散、$v^{2}$は不偏分散、$n$はサンプルサイズを表します。
ちなみに、偏差平方和$S$(平均値との差の二乗和)を自由度$n-1$で割ると不偏分散になるので、先ほどの式は次のように表現することもできます。
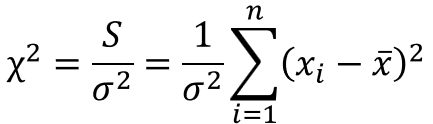
カイ二乗分布の定義の式(二乗和)に近い形となり、この統計量がカイ二乗分布に従うことのイメージが掴みやすくなったのではないかと思います。

計算式はシンプルで分かりやすいね
検定の手順
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
改善後の分散が小さくなったことを背理法で証明したいので、帰無仮説を「$H_{0}:σ^{2}=σ_{o}^{2}$」、すなわち「改善前と母分散に違いがない」と設定します。
ここで、$σ^{2}$は標本データから得られた不偏分散、$σ_{o}^{2}$は母分散を表します。
また、対立仮説は本来の目的である証明したい仮説として、「改善後の分散は改善前よりも小さくなった」とします。
$H_{0}:σ^{2}=σ_{o}^{2}$
$H_{1}:σ^{2}<σ_{o}^{2}$(片側検定)
今回の対立仮説では、$σ^{2}$が$σ_{o}^{2}$よりも大きくなる場合は調べたい対象ではないので、片側検定となります。
対立仮説を「$H_{1}:σ^{2}≠σ_{o}^{2}$(改善前後で分散に差がある)」と設定した場合には、両側検定となるので間違えないように注意しましょう。
2.検定統計量を算出する
先ほどの数式に従い、検定統計量を求めます。
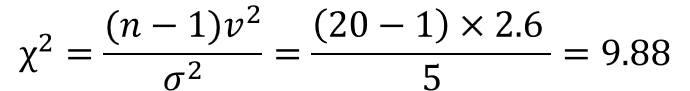
3.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
判定の指標には、カイ二乗値を用います。
通常、統計的検定では、有意水準$α=0.05$や$α=0.01$を基準として用います。
標準正規分布やt分布と違って注意が必要なのは、カイ二乗分布は横軸0を中心とした左右対称の確率分布ではないことです。
つまり、標本分散が母分散より大きいことを調べる場合に用いる上側確率のカイ二乗値と、小さいことを調べる場合の下側確率のカイ二乗値は、同じではないのです。
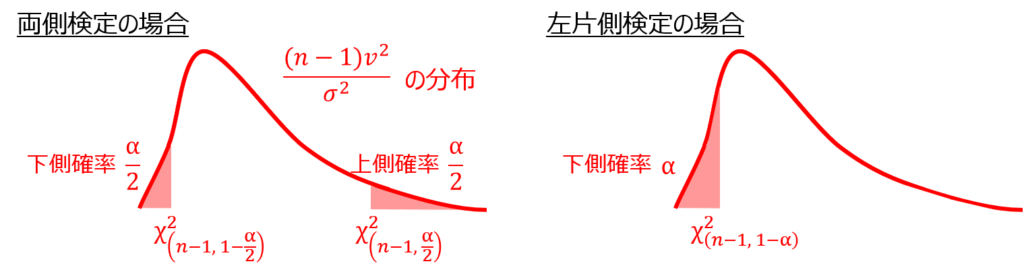
そのため、両側検定の場合には、上側確率と下側確率のそれぞれの棄却域のカイ二乗値を求める必要があります。
今回の場合は、標本分散が母分散より小さくなったことを調べる片側検定なので、下側5%、1%に該当するカイ二乗値を求めます。

上側と下側は間違えやすいから常に意識しよう
サンプルサイズ$n=20$なので、自由度$φ=19$となり、カイ二乗分布表から$φ=19$、確率$p=0.05$及び$p=0.01$となる値を読み取ります。
なお、カイ二乗分布表では上側確率に対応する確率$p$が与えられており、例えば下側5%確率を求める場合には、$1-p=0.95$と置き換えてカイ二乗値を読み取ります。
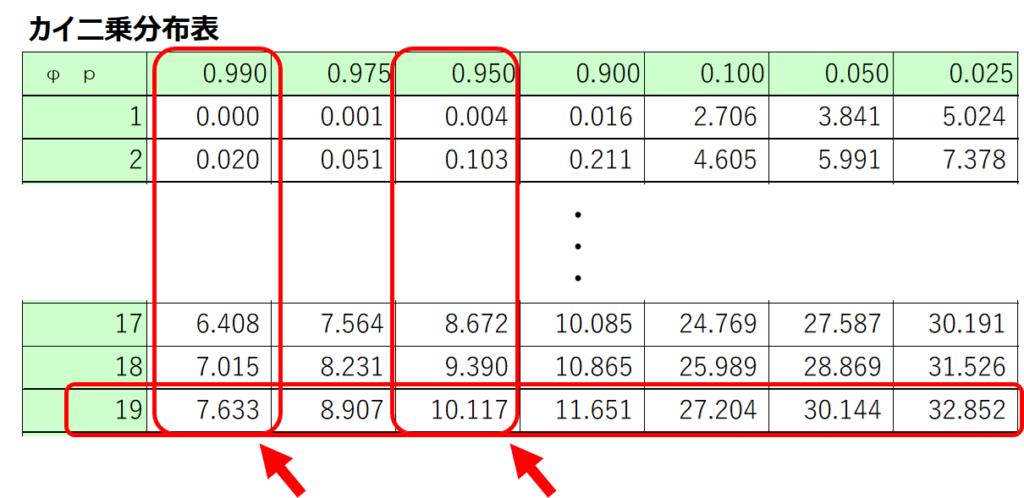
また、エクセルの場合には、カイ二乗分布の累積分布関数の逆関数を表すCHISQ.INV関数で左側確率(下側確率)、CHISQ.INV.RT関数で右側確率(上側確率)をそれぞれ求められます。

先ほどの検定統計量と比較すると、以下の関係であることが分かります。
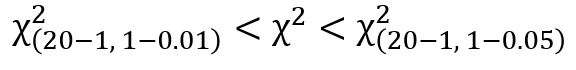
1%の棄却域には入っていないが、5%の棄却域には入っている状態、つまり有意水準5%で帰無仮説が棄却され、対立仮説が採択されるという結果となります。
4.検定の結論を導く
検定の結果から、今回の結論を出します。
「有意水準5%で改善後の分散は小さくなったと言える」
まとめ
- 1つの母分散に関する検定統計量
⇒標本の不偏分散と母分散から求めたカイ二乗値を用いる - 検定の手順
⇒仮説を設定する
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント