この記事では、適合度検定について記載していますので、参考なればうれしいです。
適合度検定は、この記事で完結して解説していますが、統計的検定の概念とメリット、登場する用語の意味など、その1から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

適合度検定とは?
まず「適合度」とは、ある観測値の構成比率の理論値があらかじめ分かっている場合において、実際に観測した値と理論値との合致する度合いのことを意味します。
文章だけでは少々理解しにくいので、具体例から紹介します。
例えば、サイコロの目の出る確率が均等であったとして、どの目の出る確率も理論値は1/6となります。
そして、実際にサイコロを何度も振ってみると、当然ながら理論値(期待度数)にぴったりと合うわけではなく、出る目の回数にズレのあることが分かります。
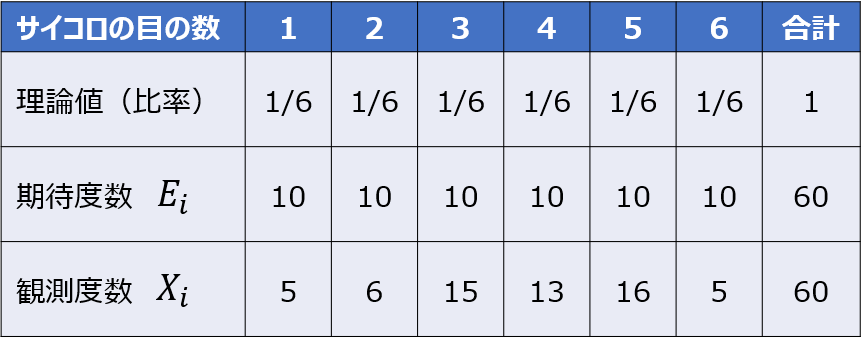
このようにサイコロの目の出る確率の理論値と実際の観測値の合致する度合いについて、検定統計量を用いて定量的に検定する、というのが適合度検定の考え方なのです。
適合度検定の手順
検定統計量
適合度検定ではカイ二乗分布の考え方を使います。
「統計的検定を習得する」シリーズを最初からご覧いただいた方は、その参の母分散の検定でカイ二乗分布は馴染みがあると思いますが、軽くおさらいをしておきます。
「カイ」は記号で「$χ$」と表され、以下の数式によって定義されます。
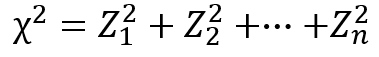
ここで、$Z_{1}~Z_{n}$は標準正規分布に従う互いに独立な確率変数を表します。
標準正規分布とは、正規分布において平均値$μ$を0、標準偏差$σ$を1として基準化したもので、$N(μ,σ^{2})$は$N(0,1)$と表記されます。
この$χ^{2}$が従う確率分布のことをカイ二乗分布と呼び、自由度$n-1$のカイ二乗分布に従うと表現されるのです。
確率変数の二乗和が従う分布なので、すなわち、「ばらつき」「分散」に関わる確率を求める場合に活用されます。
適合度検定は理論値に対する観測値の合致する度合いを調べるもので、逆に言うと観測値のズレの程度を扱う検定であり、まさに「ばらつき」を検証するカイ二乗検定の出番なのです。
なお、カイ二乗分布や母分散の検定から詳しく見たいかたは、以下の記事で紹介しています。


検定の手順
先ほどのサイコロの例を用いて、出る目に偏りがあるかどうか調べてみましょう。
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
出る目に偏りがあることを背理法で証明したいので、帰無仮説を「$H_{0}:p=1/6$」、すなわち「どの目も出る確率は同じ」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「出る目に偏りがある(すべて1/6とは限らない)」とします。
$H_{0}:p=1/6$
$ H_{1}:p≠1/6$
2.検定統計量を算出する
カイ二乗値の定義に従い、検定統計量を求めます。
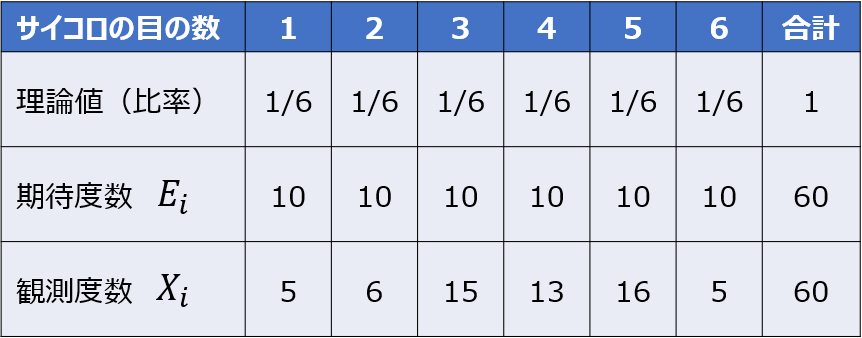
まずは、各目の出る回数の期待度数(理論値)を出します。
今回の例では、合計60回なので、仮に均等に出るとしたら10回ずつとなるはずです。
そして、次の表のように各目の理論値からのずれを求め、すべての目のずれ量を合算すると、検定統計量であるカイ二乗値が計算できます。
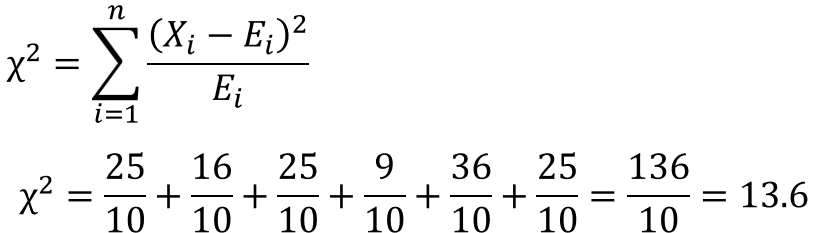
3.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
ここで用いる自由度は要素数から1を引いたものにあたるので、今回の場合は5(=6-1)となります。
判定のしかたは、母分散の検定と同じくカイ二乗表、またはエクセル関数(CHISQ.INV関数)を用いて閾値(しきい値)との大小関係を見ます。
ひとつ、適合度検定の特徴としては、理論値からのズレの程度を判定するので下側確率を見る必要はなく、上側確率を見る片側検定となることです。
今回の場合、有意水準$α=0.05$における棄却判定値は次のように読み取ることができます。
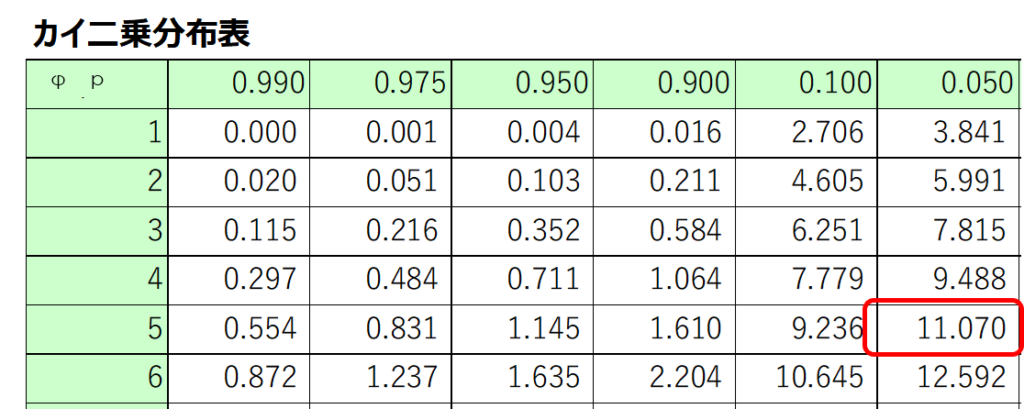

先ほどの検定統計量と比較すると、以下の関係であることが分かります。
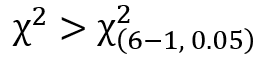
有意水準5%で帰無仮説が棄却され、対立仮説が採択される結果となります。
4.検定の結論を導く
検定の結果から、今回の結論を出します。
「サイコロの出る目に偏りがある」
まとめ
- 適合度検定
⇒ある観測値の構成比率の理論値が既知の場合において、実際に観測した値との合致する度合いを検定統計量で定量的に調べる手法 - 検定の手順
⇒仮説を設定する
検定統計量を算出する
帰無仮説の棄却/採択を判定する(上側確率の片側検定)
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント