この記事では、対応のない2つの正規分布における母平均の差の統計的検定について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
また、対応のない母平均の差の検定は、エクセルのアドインの分析ツールを用いて、簡単に検定統計量やP値を求めることができます。
分析ツールの使い方や計算式の内容についても解説しますので、参考になればうれしいです。
なお、統計的検定の概念とメリット、登場する用語の意味など、統計的検定(その1)の記事から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

対応のないデータとは?
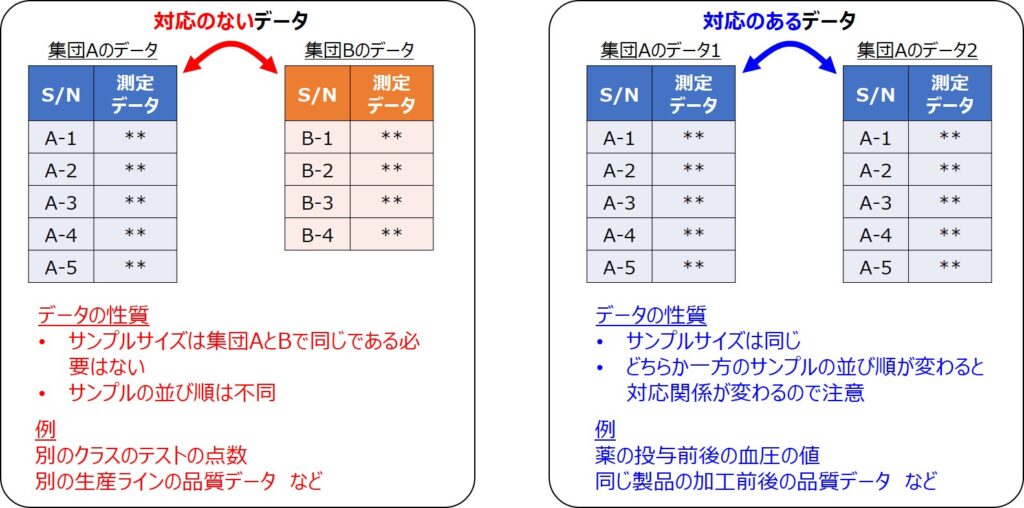
「対応のないデータ」というのは、2つの母集団における個々のデータに関連がない場合のことを表します。
例えば、2つの生産ラインで作った製品の強度の差を比較したい場合をイメージしてみましょう。
ラインAとラインBの製品からいくつかを抜き取り、破壊試験でそれぞれの強度データを取得したとします。
2つの生産ラインのデータは互いに独立な関係にあるため、サンプルサイズが同じである必要はなく、サンプリング番号を入れ替えても問題はありません。
このような性質のデータにおいて、それぞれの母平均にどの程度の差があるのか、t分布を用いて統計的検定を行うことができます。
対応のあるデータとの違い
一方で「対応のあるデータ」とは、2つの母集団のデータに関連がある場合で、例えば、とある病気の患者に薬を投与した際の効果を比較するケースなどに用いられる手法です。
そのため、2つのデータのサンプルサイズは同じであり、また、それぞれの対応関係が入れ替わらないようサンプリング番号の対応も決まっています。
「平均値の差」を求める手法としては両者は似ていますが、扱うデータの性質や計算方法が異なるので、目的にあったものを上手く使い分けできるようにしておきましょう。

名前は似てるけど検定の計算のしかたは全然違うから注意しよう
対応のない母平均の差の検定
前提条件
はじめに注意点として、今回紹介する統計的検定の前提条件を2つ説明しておきます。
①:2つの母集団は正規分布に従う
比較したい2つの母集団は正規分布に従う前提となります。
正規分布に従わない場合にはノンパラメトリック手法と呼ばれ、今回説明する検定統計量の計算式は適用できないので注意が必要です。
②:2つの母集団の分散は等しい(等分散)
母集団の分散が等しい前提での計算式となります。
等分散を仮定しないデータを扱う場合には、ウェルチ(Welch)のt検定を用いるので、取得したデータに対してあらかじめ等分散の検定でどちらを使うのか確認が必要です。
検定統計量
対応のないデータの母平均の差の確率分布は、t分布に従います。
t分布とは以下の数式により求められる統計量t値が従う確率分布のことです。
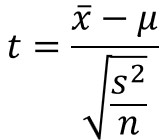
$\bar{x}$は標本平均、$μ$は母平均、$s^{2}$は不偏分散、$n$は自由度を表します。
詳しくは別の記事で解説していますので、合わせてご覧ください。

t分布では、分布の横軸(値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのT.DIST関数やt分布表で簡単に求められます。
そして、この値を検定統計量として用いることで、母平均の差に対する検定を行うことができるのです。
検定統計量は、以下の数式で表されます。
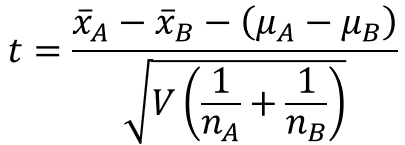
$\bar{x}_{A}$, $\bar{x}_{B}$はそれぞれの標本平均、$μ_{A}$, $μ_{B}$は母平均、$n_{A}$, $n_{B}$はサンプルサイズを表します。
また、$V$は共通分散を表し、以下の計算式で求められます。
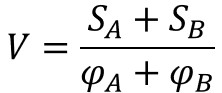
$S_{A}$, $S_{B}$は各標本の偏差平方和、$φ_{A}$, $φ_{B}$はそれぞれの自由度で$φ_{A}=n_{A}-1$, $φ_{B}=n_{B}-1$で求められます。
つまり、共通分散とは2つの標本を合わせたときの不偏分散のようなイメージとも言えます。
なお、統計的検定では、区間推定と似た考え方を用いており、検定統計量の計算式も区間推定で登場した式と近いものが多いので、検定と推定はセットで覚えておくとよいです。
対応のない母分散の差の区間推定については、以下の記事で詳しく解説していますので、合わせてご覧いただければと思います。

検定の手順
それでは、実際に母平均の差の検定をやってみましょう。
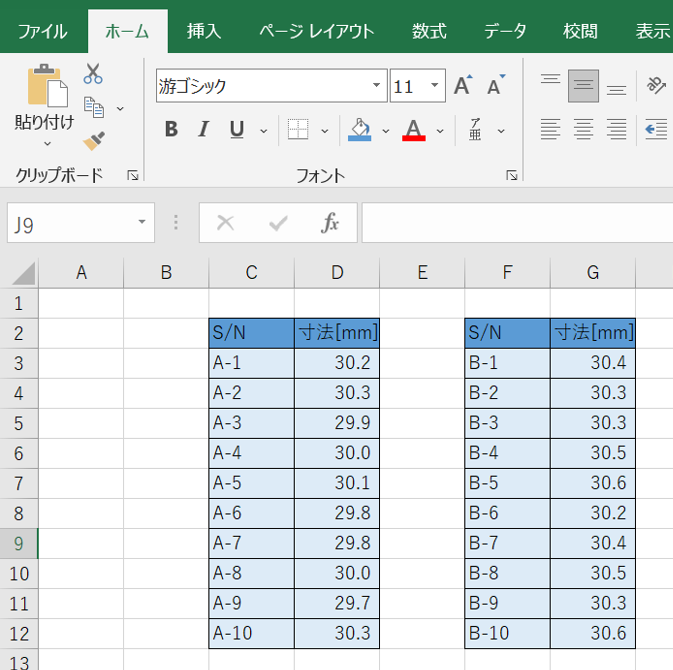
以下は、とある製品Aと製品Bを無作為に抽出し、寸法を測定した結果です。
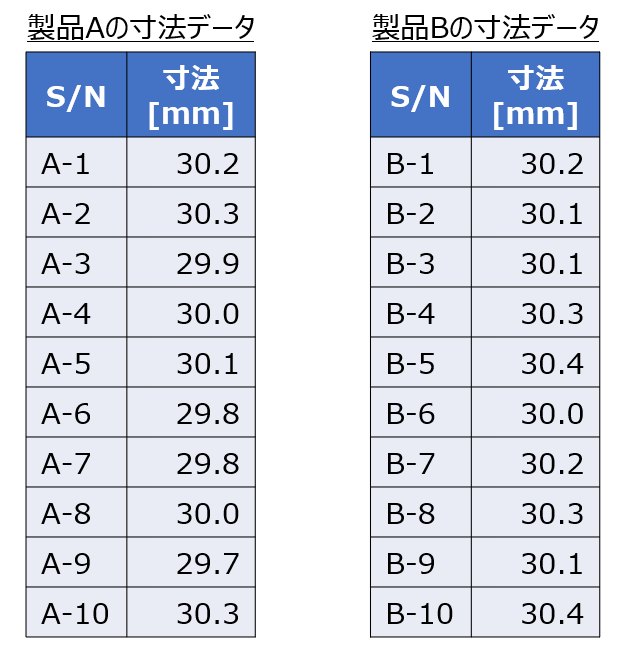
この製品Aと製品Bの寸法の分布が正規分布に従い、かつ等分散であるとするとき、母平均に差があると言えるでしょうか?
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
製品Aと製品Bの母平均に差があることを背理法で証明したいので、帰無仮説を「$H_{0}:μ_{A}=μ_{B}$」、すなわち「製品Aと製品Bの母平均に違いがない」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「製品Aと製品Bの母平均に違いがある」とします。
$H_{0}:μ_{A}=μ_{B}$
$H_{1}:μ_{A}≠μ_{B}$(両側検定)
対立仮説を「$H_{1}:μ_{A}>μ_{B}$(製品Aよりも製品Bの母平均の方が小さい)」と設定した場合には、片側検定となるので間違えないように注意しましょう。
2.共通分散を求める
次に、以下の計算式で共通分散を求めます。
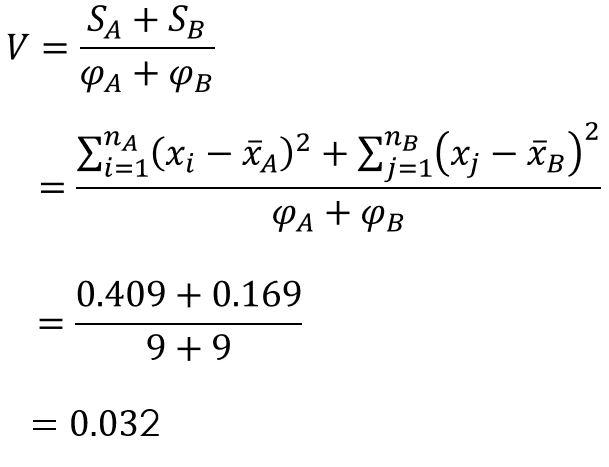
$S_{A}$、$S_{B}$は各標本の偏差平方和、$φ_{A}$、$φ_{B}$はそれぞれの自由度で$φ_{A}=n_{A}-1$、$φ_{B}=n_{B}-1$で求められます。
エクセルを用いる場合、偏差平方和はDEVSQ関数を使えば元データを指定するだけで簡単に計算することができます。
3.検定統計量を算出する
定義の数式に従い、検定統計量$t_{0}$を求めます。
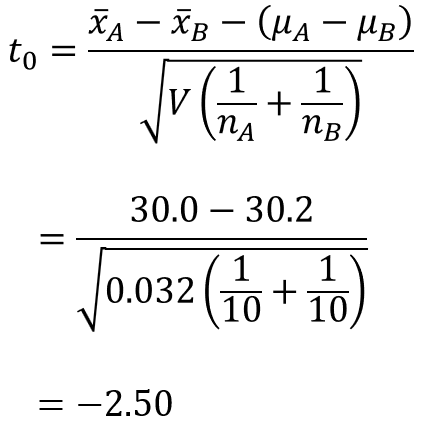
4.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
両側検定の場合、先ほど求めた検定統計量$t_{0}$と有意水準に対応するt値との間に、以下の関係が成り立つと帰無仮説が棄却されます。
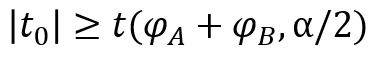
t分布表から自由度18と両側確率0.05におけるt値(2.101)を読み取ります。
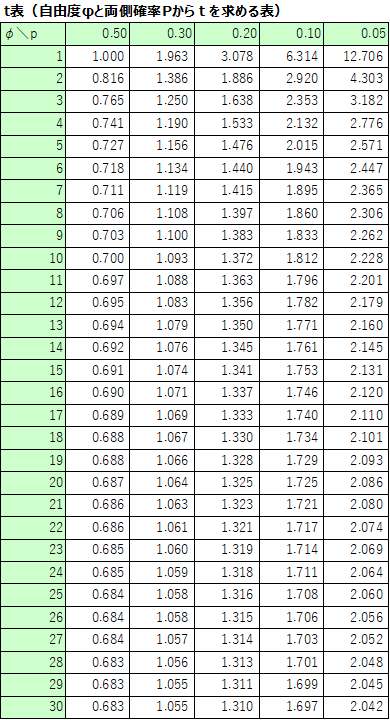
ちなみに、エクセルのT.INV.2T関数やT.INV関数を用いてもt値を求めることができます。
T.INV.2T関数とは、t分布の両側確率の逆関数を表すもので、今回の場合、=T.INV.2T(0.05,18)と入力すると同じ値が得られます。
また、T.INV関数は下側(左側)確率の逆関数を表すもので、片側検定を行う場合に用いると有効です。
5.検定の結論を導く
検定統計量$t_{0}$の絶対値が棄却限界値よりも大きく、帰無仮説が棄却されて対立仮説が採択されます。
つまり「有意水準5%で母平均に違いがあると言える」となります。
エクセルを用いた検定
エクセルにはデータ分析のツールが備わっており、ヒストグラムや回帰分析、統計的検定を手軽に行う機能があります。

便利な機能だから覚えておこう
アドインの設定
エクセルをインストールした初期状態ではアドインが無効になっているので、まず使いたい分析ツールのアドインを有効にします。
「ファイル」>「その他」>「オプション」からExcelのオプションを立ち上げ、「アドイン」のタブを選択します。
「設定」をクリックすると、有効なアドインが表示されるので、「分析ツール」のチェックボックスを入れて「OK」を押します。
すると、このように「アクティブなアプリケーション ドメイン」に分析ツールが追加されます。
分析ツールの使い方
アドインの設定ができたところで、実際に分析ツールを使ってみましょう。
まずはツールを起動する前に、検定に用いるデータをエクセルに入力します。
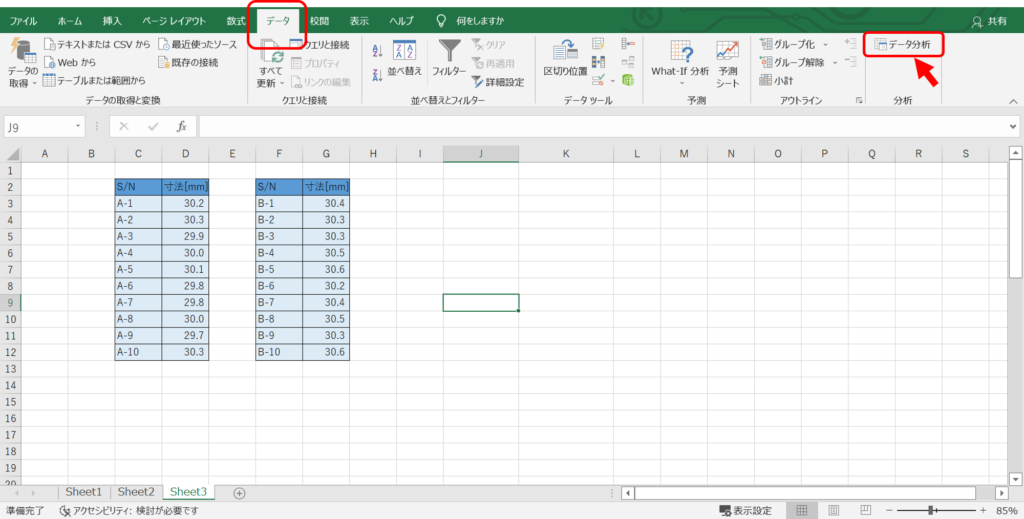
「データ」タブを選択し、「データ分析」をクリックして立ち上げます。
「t検定:等分散を仮定した2標本による検定」を選択して「OK」を押します。
変数1と変数2の入力範囲に対応するデータを選択し、有意水準αを設定します。
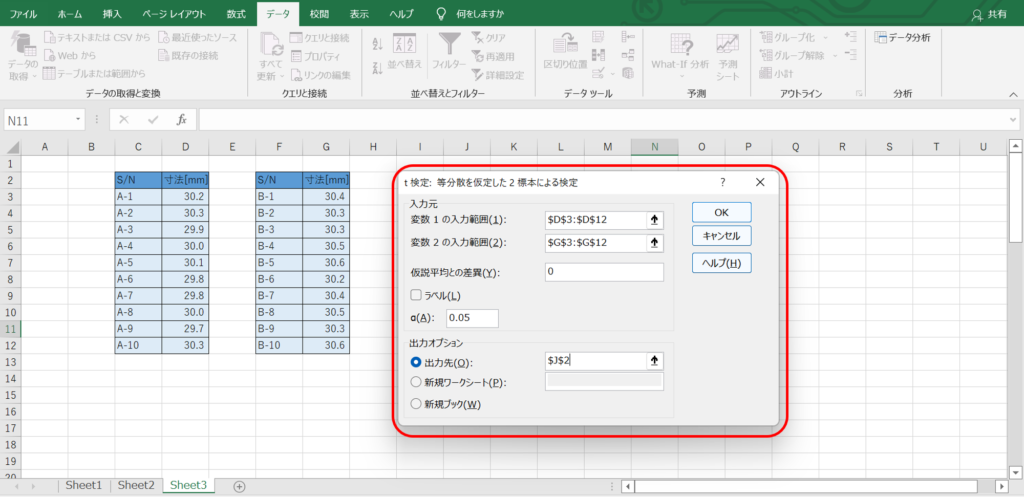
仮説平均との差異については、今回の場合、平均値に差がないことを示したいのでゼロとします。
結果を記載する出力先を設定して、「OK」を押します。
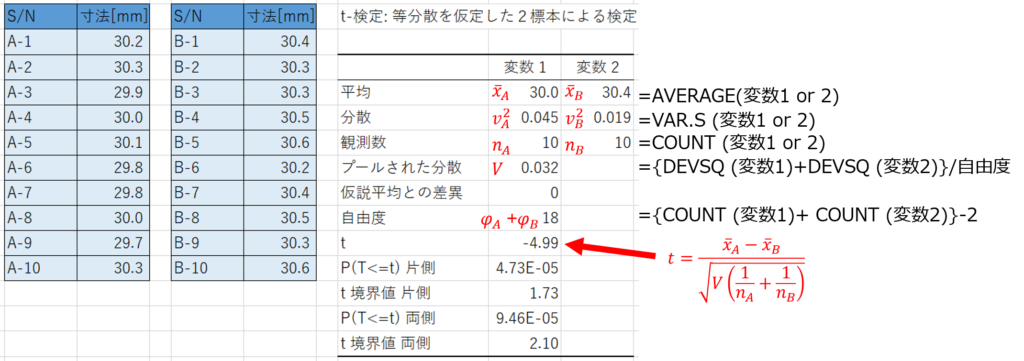
結果の見かたと計算式
たったこれだけの操作で、自分で複雑な計算をすることなく、簡単にt検定を行うことができるのですが、初見では結果を読み解くことが少し難解です。
手軽に検定できるメリットは大きいですが、用語や計算結果の意味を正しく理解していないと、解釈を誤る可能性があるので注意が必要です。
ひとつずつ見ていきましょう。
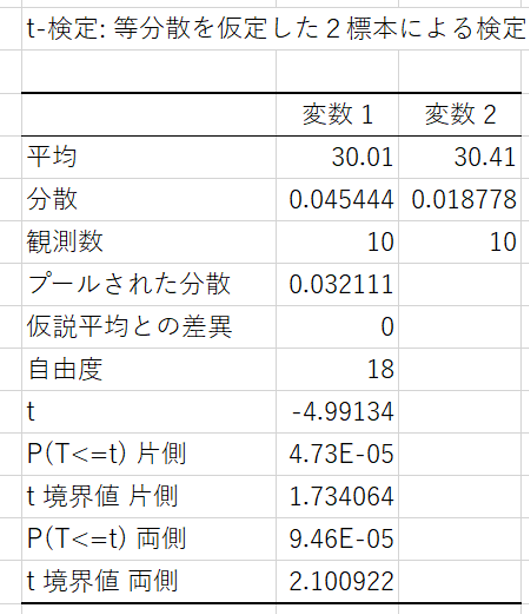
平均:標本データの平均値
分散:標本データの不偏分散
観測数:標本データのサンプルサイズ
プールされた分散:共通分散
t:標本データから求めた検定統計量
t境界値片側:片側検定において有意水準αとなるt値
t境界値両側:両側検定において有意水準αとなるt値
つまり、帰無仮説の棄却/採択を判断するには、「t」と「t境界値片側(または両側)」を比べれば良いのです。
t境界値よりも検定統計量tの絶対値の方が大きい場合、確率的には稀な事象を表しますので、母平均の差がない可能性が極めて低いことを意味します。
また、「P」は確率(Probability)を表す統計量であり、標本データから求めた検定統計量「t」の値に該当する確率を意味しています。
P値が有意水準α以下(例えば0.05や0.01以下)であれば帰無仮説は棄却されることになります。
つまり、P値さえ見ておけば、棄却/採択を瞬時に判断できるのですが、単に0.05以下であればよいと覚えるのではなく、意味を理解しておきましょう。
ここまで説明した用語について、エクセル関数で計算式を表すと以下のようになります。
まとめ
- 対応のない母平均の差に関する検定統計量
⇒t分布のt値を用いる
ただし、母集団は正規分布に従うこと、等分散であることが前提条件 - 検定の手順
⇒仮説を設定する
共通分散を求める
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント