「共分散って、どういう意味?」
「定義だけではイメージが掴めない」
「公式とエクセルでの計算手順を知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
共分散とは、2種類のデータの関係の強さを表す指標のことです。
「相関がある」とか「相関がない」といった表現は、標本調査の中で一度は耳にしたことがある方も多いと思います。
共分散は、相関(関係)のありなしを表す基本的な指標であり、統計データを取り扱う上での知っておくべき基礎知識の一つです。
この記事では、共分散の定義と計算例、散布図を用いた共分散の概念、相関係数との関係、エクセルでの求め方について解説しています。
初心者の方にもわかりやすいよう、できるだけ手順を踏んで説明しますので、ぜひ最後まで読んで参考にしていただければと思います。
共分散とは?
定義
共分散とは、2種類のデータの関係の強さを表す指標のことで、2変数の偏差の積を平均することで求められます。
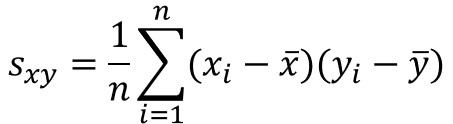
$n$はデータの総数、$x_{i}$と $y_{i}$は個々のデータ、$\bar{x}$と $\bar{y}$は平均値を表します。
$s_{xy}$と表記する他に、共分散の英語を意味するCovarianceの頭文字を取って$Cov(x,y)$と表現することもあります。
2種類のデータから関係の強さを調査したい場合、取得した元のデータを眺めていても、何も得られません。
関係の強さを数値化して定量的に示すことが必要で、その指標の一つとして共分散が用いられるのです。
後ほど詳しく説明しますが、エクセルを用いれば、共分散や相関係数は関数一つで簡単に求めることができます。
しかし、計算式の意味や導出の過程をきちんと理解していないと、単に数値が計算結果として得られるだけで、結果の妥当性を判断することもできません。
そのため、以降では具体例を示しながら、共分散のイメージを感覚的に捉えられるよう、順を追って解説していきます。
計算例

数式だけ見てもイメージが掴めない・・
「共分散は、2変数の偏差の積を平均」と定義を示されても感覚的に理解しにくいと思うので、さっそく具体例を用いて説明します。
そもそも、「偏差」って何?といった疑問もあると思いますので、具体例の中で説明していきます。
例えば、とあるクラスで実施した数学と理科のテストの点数を題材に挙げます。
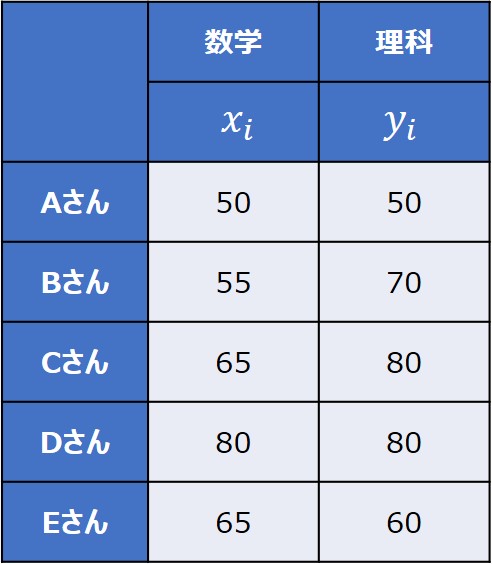
それでは、実際に共分散を求めていきましょう。
1.$x$と$y$の平均値を求める
まずは、2変数それぞれの平均値を求めます。
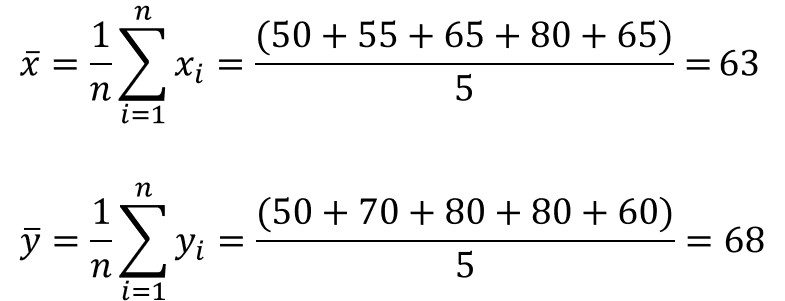
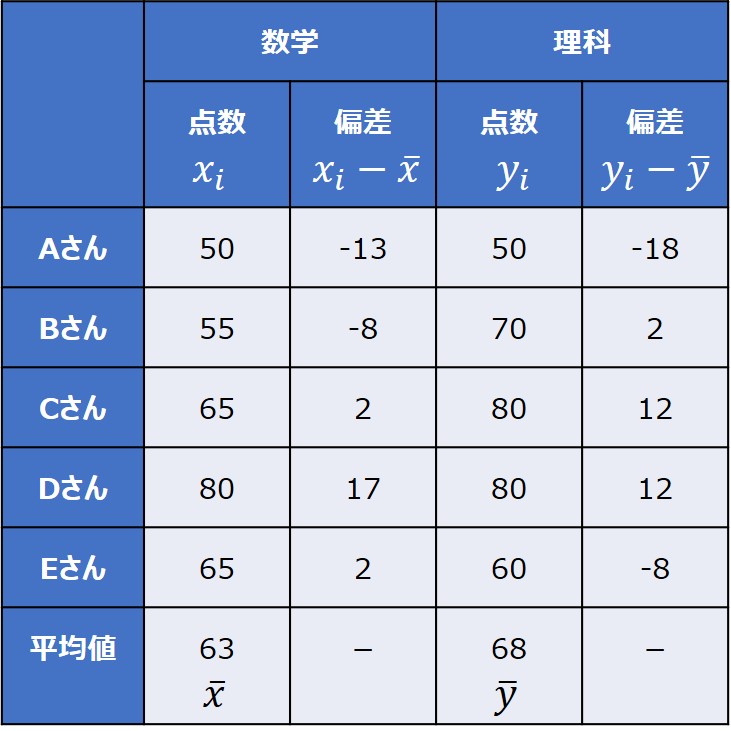
横軸に数学の点数、縦軸に理科の点数を取った散布図に、2変数の平均値を記載すると以下のようになります。
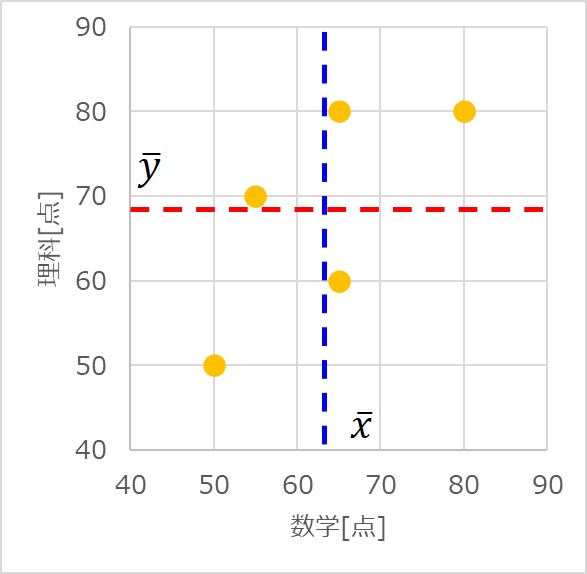
青点線が数学の平均点の線($x=63$)、赤点線が理科の平均点の線($y=68$)となります。
2.各データの偏差を求める
「偏差」とは、データの偏りのことを意味し、つまり平均との乖離の程度を表します。
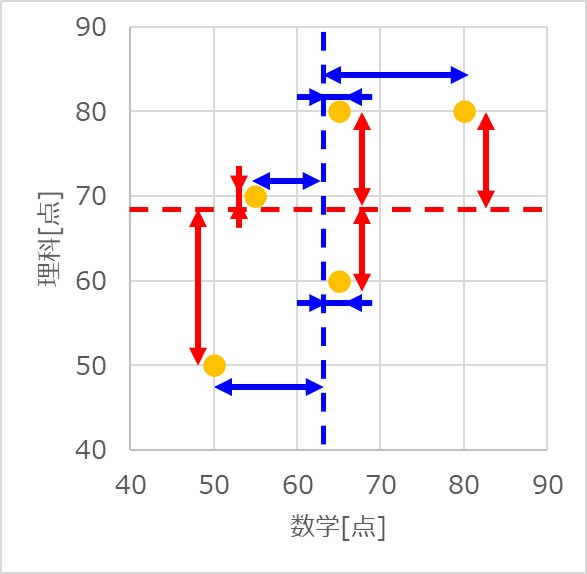
計算の仕方は簡単で、$x$と$y$それぞれの変数に対し、個別データから平均点を引いたものが偏差になります。
散布図のイメージで表すと以下の通りで、平均点との差分をそれぞれのデータに対して求めていくことになります。
3.偏差の積の平均を求める
すべてのデータに対して偏差が計算できたら、最後に偏差の積の平均、つまり共分散を計算します。
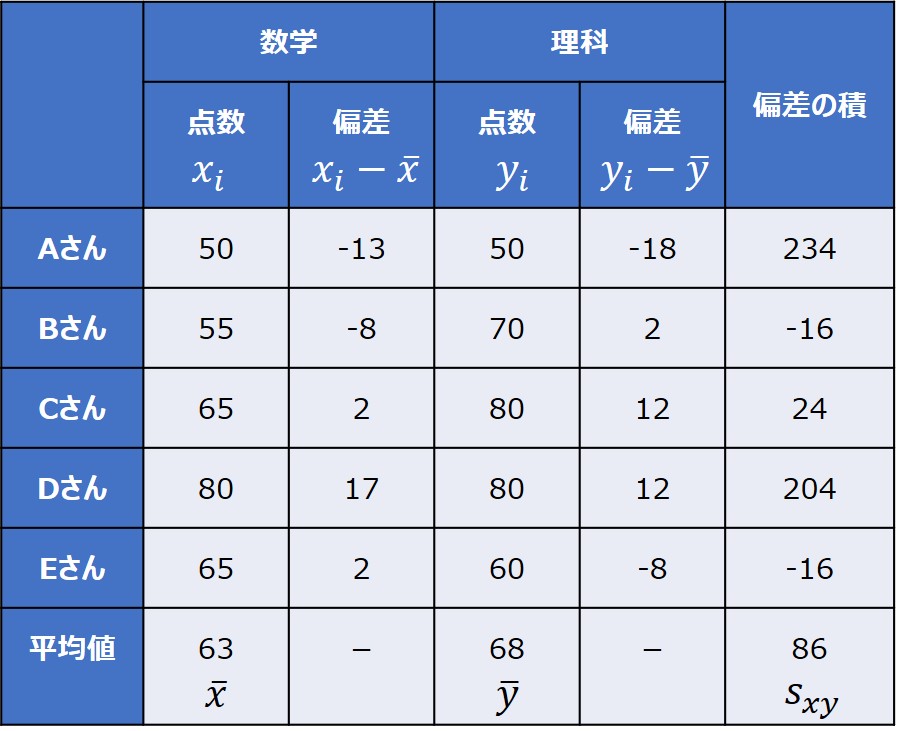
今回の事例では、共分散の値は$ s_{xy}=86$と求めることができました。
共分散を視覚的に捉える
偏差の積とは?

もう少し見た目で理解できないかなぁ
偏差の積というのは、次のように平均点のデータと各データを対角の点に取った長方形の面積を求めるイメージに近いです。
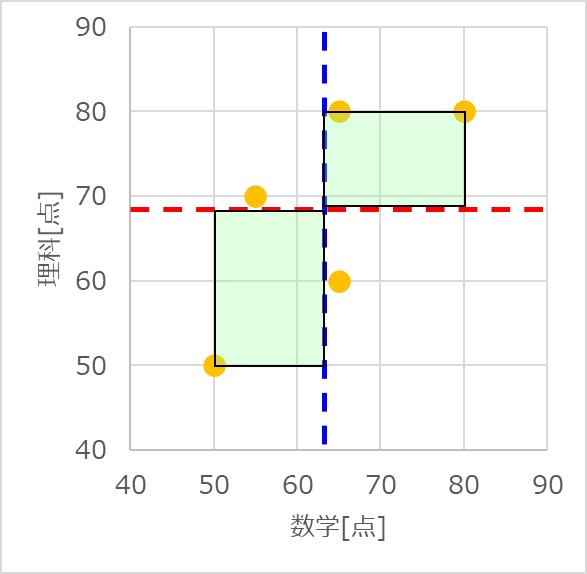
そして、平均値の点を原点として見たときに、$x$も$y$も大きい場合はプラス、$x$と$y$いずれか一方が大きい場合はマイナス、どちらも小さい場合はプラスになります。
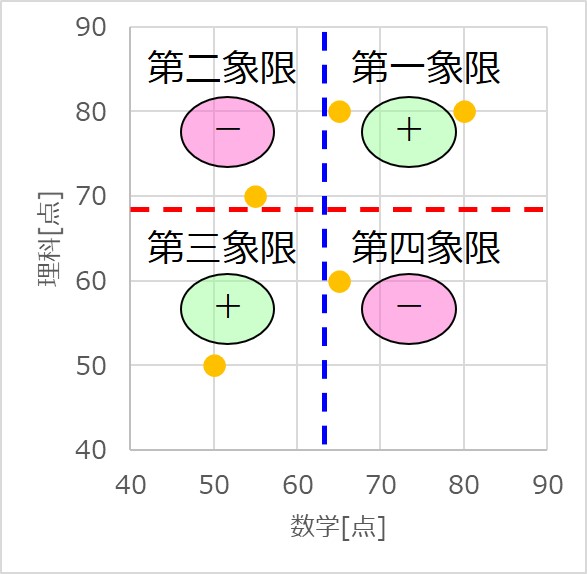
つまり、第一、第三象限ではプラス、第二、第四象限ではマイナスになるということです。
積の平均値とは?
積の平均を求めるということは、全体的な分布としてマイナス象限に偏っているのか、プラスに偏っているのか、あるいは平均するとゼロに近いのか、傾向を掴むことにつながります。
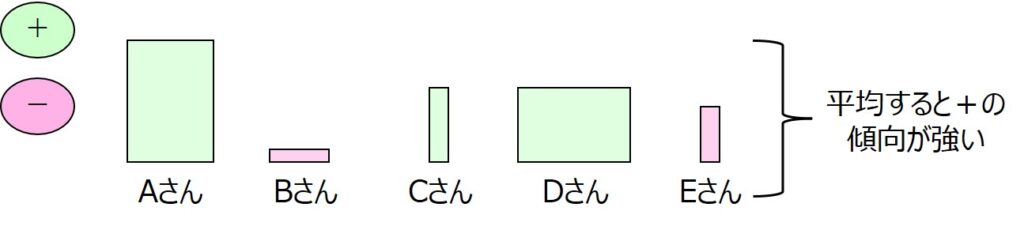
例えば、プラス側に偏った結果となる場合は、以下のように全体として第一、第三象限にプロットが多くなるはずです。
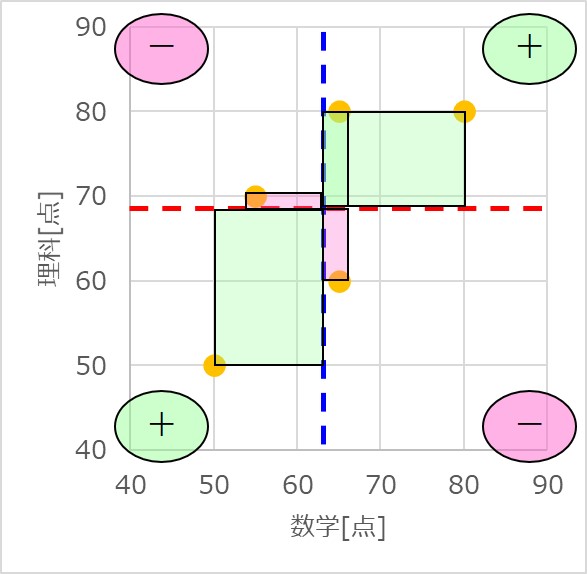
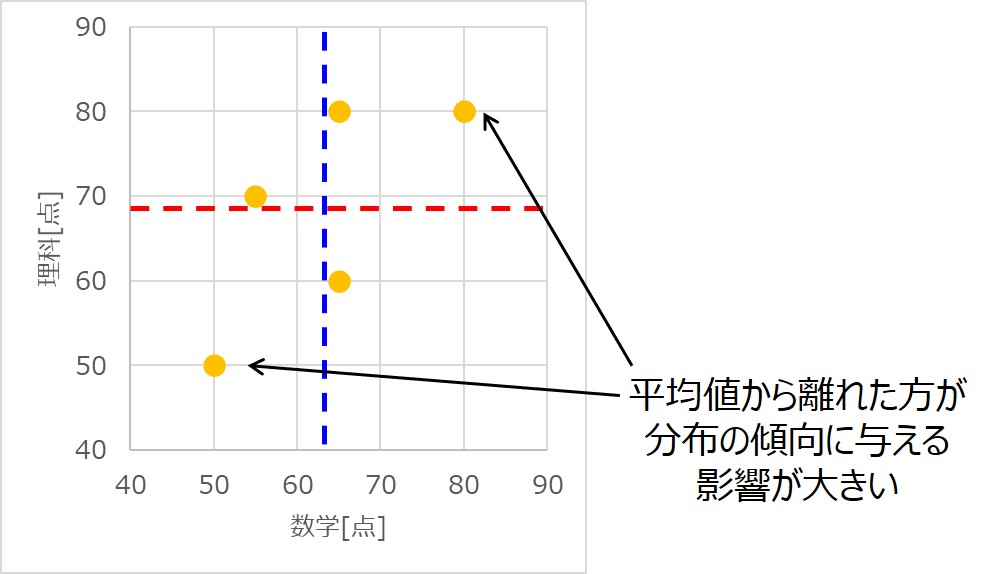
さらには、とある一点のデータが平均値から大きく離れている場合には、共分散の値に大きく影響を及ぼします。
これは、狭い範囲に密集したデータよりも、広いレンジで分布したデータの方が全体の分布に与える影響が大きいことを意味しているのです。
共分散と相関係数
相関係数とは?
共分散は2種類のデータの関係の強さを表す指標ですが、これと似た意味の指標として相関係数があり、以下の数式で定義されます。
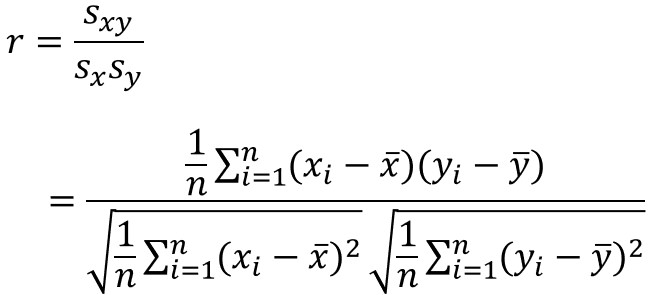
$r$は相関係数、$s_{x}$は$x$の標準偏差、$s_{y}$は$y$の標準偏差を表します。
共分散は偏差の積の平均値で定義されるので、単位は元データの単位の二乗となり、つまり先ほどの具体例で言うと、[点数の二乗]となります。
例えば、データの形式が長さや重さの場合、当然単位は変わりますし、100点満点と10点満点のテストでも共分散の値は大きく変わってきます。
これでは、関係の強さを同じ基準で比較することができません。
そこで、共分散を標準化して単位を無次元化した指標として相関係数が用いられ、-1~1の値として表現されるのです。
相関係数が1となる場合
では、相関係数が1というのは、どのような場合を表すのでしょうか。
先ほどの数式で$r=1$と置くと、以下のように変換できます。
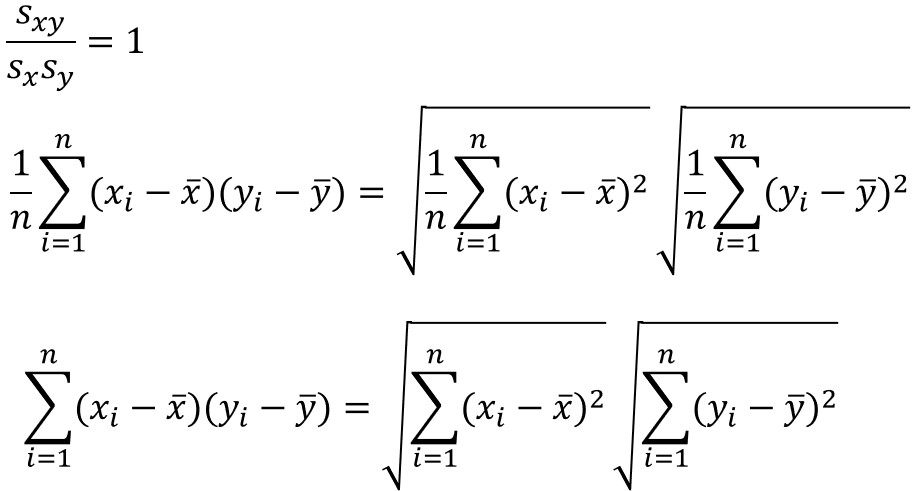
この数式は、コーシー・シュワルツの不等式を用いれば、意味を理解することができます。
コーシー・シュワルツの不等式とは、以下の関係が成り立つ性質を表したものです。

相関係数の式に置き換えると、等号成立条件は以下のように表されます。
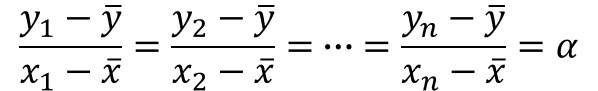
$\bar{x}$、 $\bar{y}$を原点にシフトした座標系を$\acute{x}$、 $\acute{y}$とすると $\acute{y}= α\acute{x}$と表すことができ、すなわち、 $\bar{x}$、 $\bar{y}$ を原点に全てのデータが一直線に並んだ状態のことを意味します。
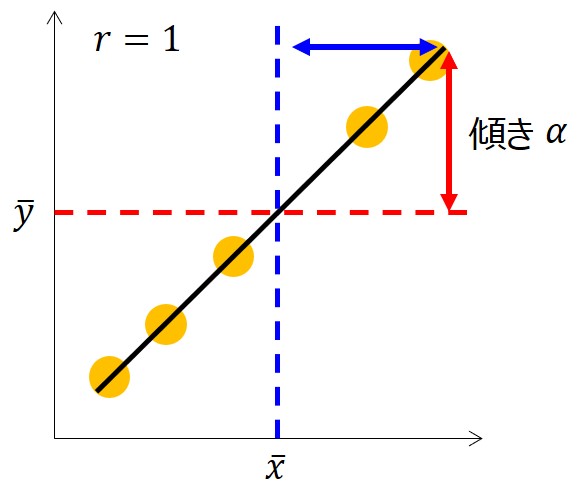
相関係数がマイナス1になるのも同様で、 $\acute{y}= α\acute{x}$において$α$の値がマイナス(右下がり)になる状態のことを意味しています。
このように考えれば、相関係数$r$が-1~1の範囲を取る指標であることが、イメージとして理解できますね。

共分散も相関係数も散布図で見れば分かりやすいね
共分散の公式
共分散の値は、最初に説明した定義の式の他に、以下の数式でも求めることができます。
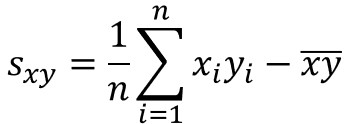
この式において$y=x$と置くと、分散の公式と同じになります。
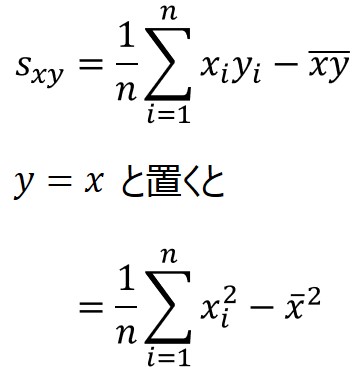
ちなみに、分散の公式は以下の変換により求められます。
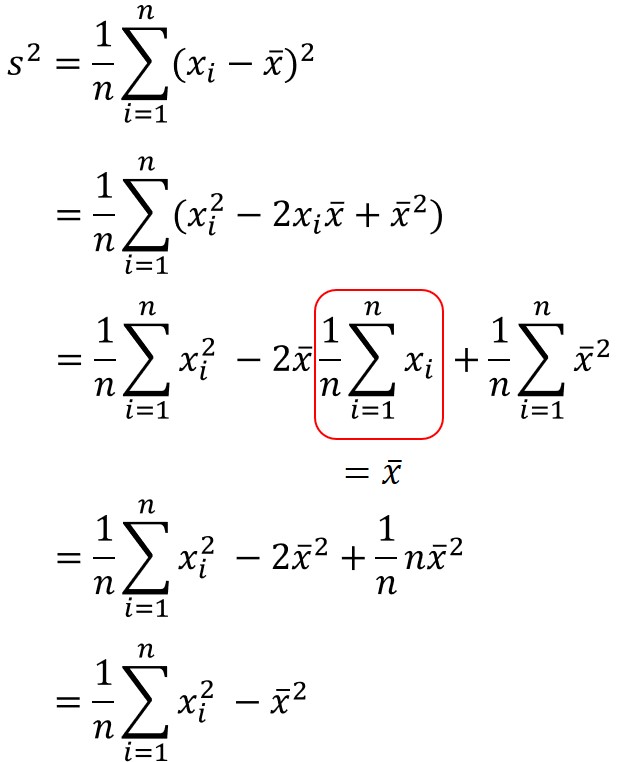
つまり、共分散の公式は分散の定義の式をより一般化したものと解釈すると良いでしょう。
共分散の公式を用いて、先ほどの具体例の共分散を求めると以下のようになります。
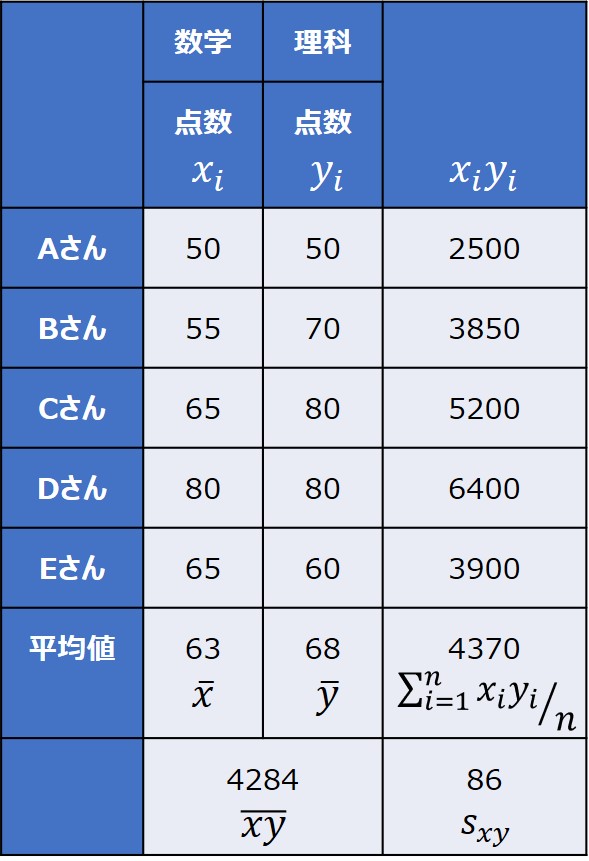
同じ値が得られましたね。
なお、共分散の公式は以下のように表記されることもあります。
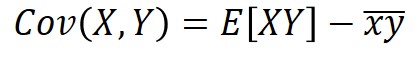
$E(X)$は$X$の期待値を意味します。
確率分布における期待値というのは、平均値のことを表すので、同じことを別の記号で表現しているだけです。
確率分布の期待値に関しては、別の記事で紹介していますので、合わせてご覧ください。

エクセルでの求め方
エクセルで共分散を求める場合には、COVARIANCE.P関数を用いると簡単に計算できます。
COVARIANCEとは共分散を英語で表記したもので、2変数の元データの配列を指定するだけで計算できます。
COVARIANCEの後ろのPは母集団の共分散を求める場合に使う関数で、標本の共分散(不偏共分散)を求める場合には、COVARIANCE.S関数を用います。
不偏分散は標本調査の不確かさを含めた統計量となるので、データの大きさ$n$の影響を受けて母集団の共分散よりも大きい値となります。
ちなみに、相関係数を求める場合には、CORREL関数で2変数の配列を指定すれば計算できます。

まとめ
- 共分散
⇒2種類のデータの関係の強さを表す指標のことで、2変数の偏差の積の平均値 - 相関係数
⇒共分散を標準化して単位を無次元化した指標、-1~1の値を取る - エクセルでの共分散の求め方
⇒母集団の共分散:COVARIANCE.P関数
不偏共分散:COVARIANCE.S関数
相関係数:CORREL関数
共分散も相関係数もエクセルを用いれば簡単に計算できますが、きちんと定義を知った上で使いこなすことが重要です。
四則演算で電卓でも計算できるので、ぜひ一度、定義を振り返って実践してみてはいかがでしょうか。





コメント