この記事では、対応のない2つの正規分布における母平均の差の信頼区間の計算方法、計算式の構成について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
対応のないデータの母平均の差の信頼区間は、この記事で完結して解説していますが、標本調査の考え方など、区間推定(その1)の記事から段階を追って説明しています。
さまざまな区間推定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

対応のないデータとは?
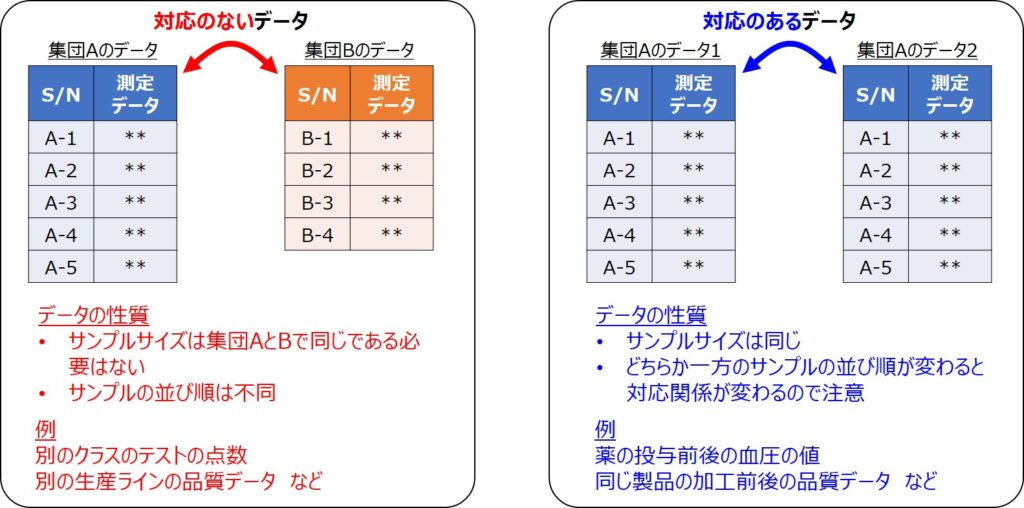
「対応のないデータ」というのは、2つの母集団における個々のデータに関連がない場合のことを表します。

何だかピンと来ないなぁ
例えば、2つの生産ラインで作った製品の強度の差を比較したい場合をイメージしてみましょう。
ラインAとラインBの製品からいくつかを抜き取り、破壊試験でそれぞれの強度データを取得したとします。
2つの生産ラインのデータは互いに独立な関係にあるため、サンプルサイズが同じである必要はなく、サンプリング番号を入れ替えても問題はありません。
このような性質のデータにおいて、それぞれの母平均にどの程度の差があるのか、t分布を用いて信頼区間を求めることができます。
対応のあるデータとの違い
一方で「対応のあるデータ」とは、2つの母集団のデータに関連がある場合で、例えば、とある病気の患者に薬を投与した際の効果を比較するケースなどに用いられる手法です。
そのため、2つのデータのサンプルサイズは同じであり、また、それぞれの対応関係が入れ替わらないようサンプリング番号の対応も決まっています。
「平均値の差」を求める手法としては両者は似ていますが、扱うデータの性質や計算方法が異なるので、目的にあったものを上手く使い分けできるようにしておきましょう。
母平均の差の信頼区間の求め方
前提条件
はじめに注意点として、今回紹介する区間推定の前提条件を2つ説明しておきます。
①:2つの母集団は正規分布に従う
比較したい2つの母集団は正規分布に従う前提での区間推定となります。
正規分布に従わない場合にはノンパラメトリック手法と呼ばれ、今回説明する区間推定の計算式は適用できないので注意が必要です。
②:2つの母集団の分散は等しい(等分散)
母集団の分散が等しい前提での計算式となります。
等分散を仮定しないデータを扱う場合には、ウェルチ(Welch)のt検定を用いるので、取得したデータに対してあらかじめ等分散の検定でどちらを使うのか確認が必要です。
信頼区間の計算式
対応のないデータの母平均の差の確率分布は、t分布に従います。
t分布とは以下の数式により求められる統計量t値が従う確率分布のことです。
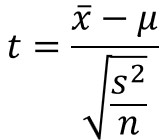
$\bar{x}$は標本平均、$μ$は母平均、$s^{2}$は不偏分散、$n$はサンプルサイズを表します。
詳しくは別の記事で解説していますので、合わせてご覧ください。

t分布では、分布の横軸(値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのT.DIST関数やt分布表で簡単に求められます。
そして、この値を係数として用いることで、信頼度○○%の信頼区間の幅を計算することができるのです。
母平均の差の95%信頼区間は、以下の数式で表されます。
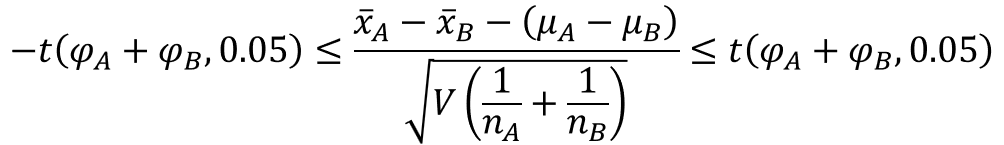
$\bar{x}_{A}$, $\bar{x}_{B}$はそれぞれの標本平均、$μ_{A}$, $μ_{B}$は母平均、$n_{A}$, $n_{B}$はサンプルサイズを表します。
また、$V$は共通分散を表し、以下の計算式で求められます。
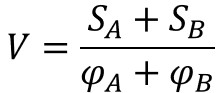
$S_{A}$, $S_{B}$は各標本の偏差平方和、$φ_{A}$, $φ_{B}$はそれぞれの自由度で$φ_{A}=n_{A}-1$, $φ_{B}=n_{B}-1$で求められます。
つまり、共通分散とは2つの標本を合わせたときの不偏分散のようなイメージとも言えます。

結局まとめて考えればいいってことだね
計算の手順
それでは、実際に母平均の差の区間推定をやってみましょう。
以下は、とある製品Aと製品Bを無作為に抽出し、寸法を測定した結果です。
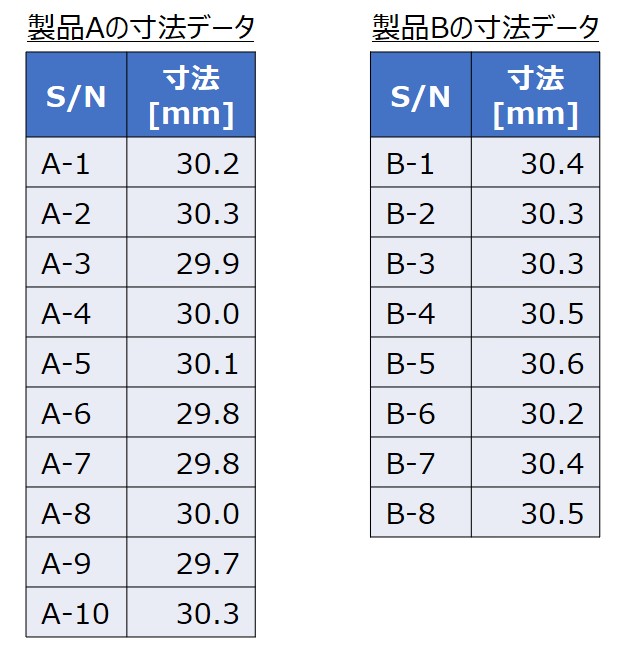
この製品Aと製品Bの寸法の分布が正規分布に従い、かつ等分散であるとするとき、母平均の差の95%信頼区間はいくらとなるでしょうか?
1.標本平均を求める
まず、2つのサンプルデータに対する標本平均を計算します。
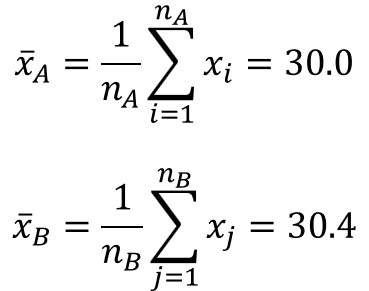
2.共通分散を求める
次に、以下の計算式で共通分散を求めます。
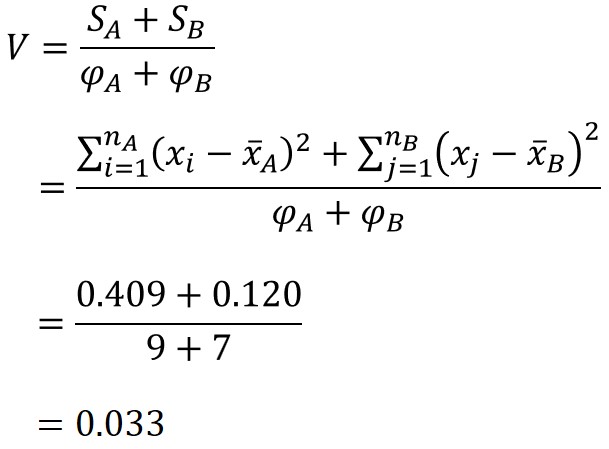
$S_{A}$, $S_{B}$は各標本の偏差平方和、$φ_{A}$, $φ_{B}$はそれぞれの自由度で$φ_{A}=n_{A}-1$, $φ_{B}=n_{B}-1$で求められます。
エクセルを用いる場合、平方和はDEVSQ関数を使えば元データを指定するだけで簡単に計算することができます。
3.t値を求める
自由度と信頼度に対応するt値を求めます。
この自由度とは、2つのサンプルデータの自由度を合算したもので、今回の場合では$φ_{A}=9$, $φ_{B}=7$なので、$φ=16$となります。
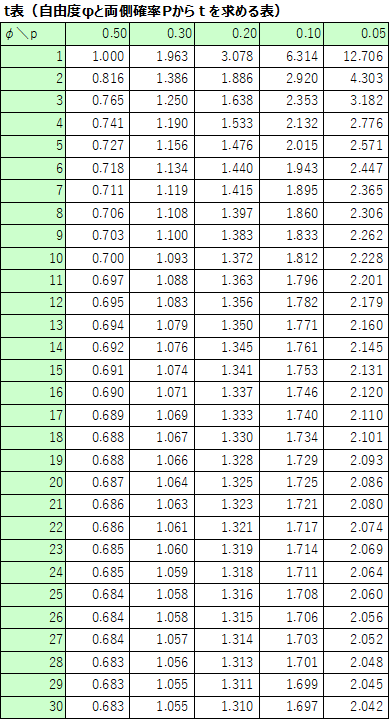
また、信頼度に対応するt値をt分布表(t表)から読み取ります。
t表とは、横軸に確率$p$、縦軸に自由度$φ$を取って、マトリックスの交差する箇所に対応するt値が記載されている表です。
t分布表で表す確率$p$は、t値に対する両側確率を意味します。
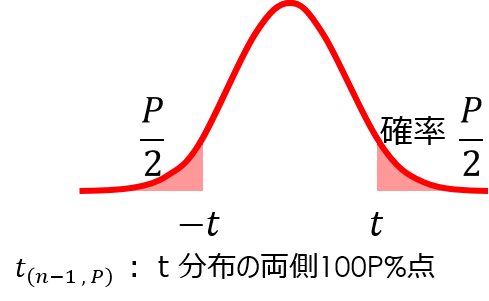
今回の場合、求めたい信頼区間は95%(0.95)となるので、自由度$φ=16$の両側確率に対応するt値を読み取ると、$t=2.120$と求めることができました。
4.信頼区間を計算する
母平均の差の信頼区間の式に信頼度95%のt値を入れると、以下の不等式が成立します。
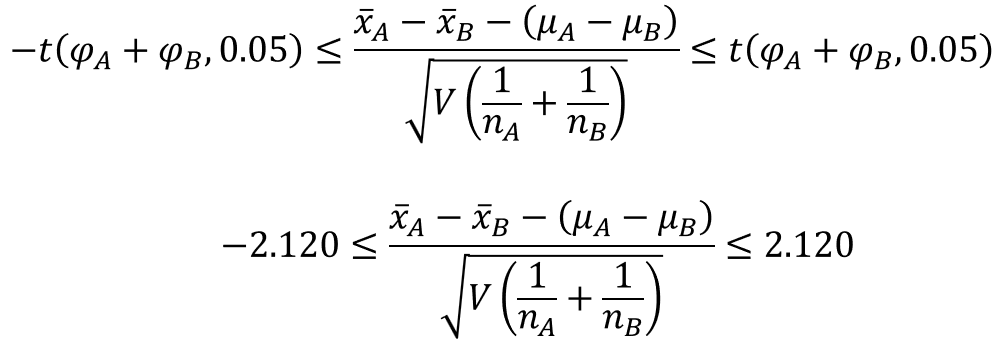
そして、これを母平均の差$(μ_{A}-μ_{B})$に対して変換すると以下のようになります。
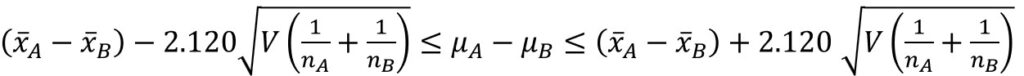
あとは、標本平均、共通分散、サンプルサイズを代入すると、母平均の差の信頼区間は以下のように求めることができました。
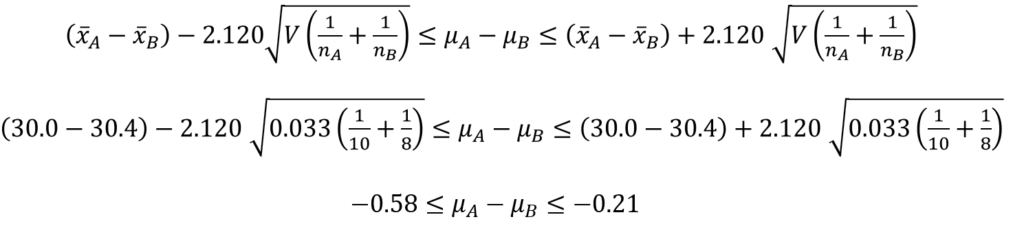
まとめ
- 母平均の差の信頼区間の求め方
⇒t分布のt値を用いる
ただし、母集団は正規分布に従うこと、等分散であることが前提条件 - 計算の手順
⇒標本平均を求める
共通分散を求める
信頼度に対応するt値を求める
母平均の差の推定値を計算する
最後まで読んでいただき、ありがとうございました。




コメント