「区間推定って何だかむずかしそう」
「母平均の信頼区間の計算式を知りたい」
「分散既知とか未知って、どう関係するの?」
このような疑問や悩みをお持ちの方に向けた記事です。
母平均の信頼区間を求める場合、母分散が既知の場合には標準正規分布、未知の場合にはt分布を使う方法に分かれます。
この記事では、それぞれの方法に対する母平均の信頼区間の計算方法、計算式の構成について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
区間推定って難しそうなイメージで、何だか取りつきにくいという方にとって、実践に移すための参考になればうれしいです。
標本平均の分布の考え方
母集団から標本をサンプリングして平均値を求める場合、必ず母集団の真の値に対してズレ(標本誤差)が生じます。

母集団の真の値を求めるには、集団の個体を全て調べる全数調査を行うしかないのですが、これには膨大な労力と時間を費やすことになります。
そもそも、ピタリと合った真の値が必要なケースは、普段の仕事や日常生活でそれほど多く出くわすでしょうか?
例えば、母集団の平均値は○○%の確率で□□~△△の範囲に収まる、といった推定値で情報としては十分であることが多いのではないでしょうか。

「だいたい」で分かれば十分なことも多いもんね
このように費用対効果を踏まえて、標本調査から母集団の平均値を推定する(予想する)事例は多くあり、例えばテレビの視聴率の調査や工場の抜取検査などが挙げられます。
そして、平均値を理論的かつ定量的に推定するにあたって、確率分布の考え方が活用されるのです。
統計学では「母平均が○○%の確率で□□~△△の範囲に収まる」と表現しますが、○○%を信頼度、□□~△△の範囲のことを信頼区間と呼びます。
また、標本から母集団を推定することを区間推定と呼び、以下のような概念になります。
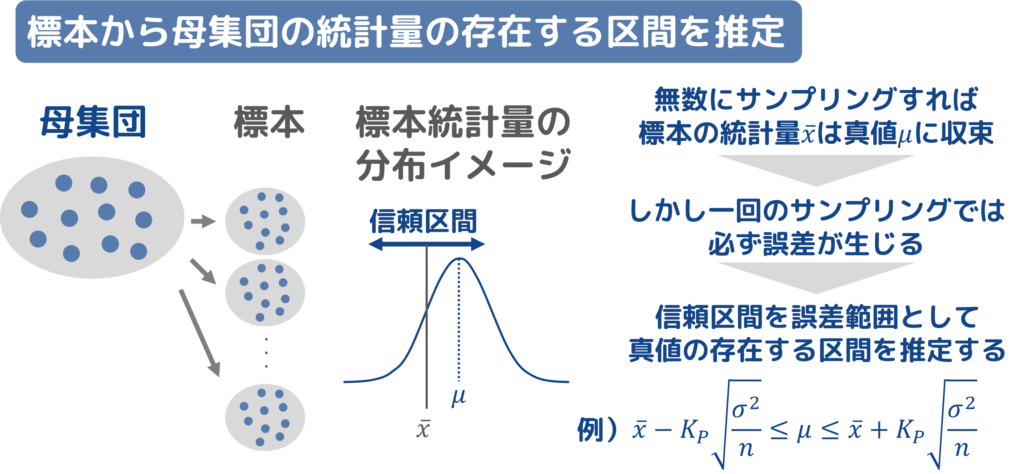
以降では、標本調査から母集団の平均値の信頼区間を求めるにあたって、母分散(母集団の分散)が既知の場合と未知の場合、2つに分けて計算手順と計算式を解説していきます。
母分散が既知の場合
信頼区間の計算式
母分散が既知の場合、標本平均の分布は標準正規分布$N(0,1)$に従います。
標準正規分布とは、正規分布を標準化したもので、標本平均から母平均を差し引いて中心値をゼロに補正し、さらに標準偏差で割って単位を無次元化する処理のことを表します。
詳しくは別の記事で紹介していますので、合わせてご覧ください。

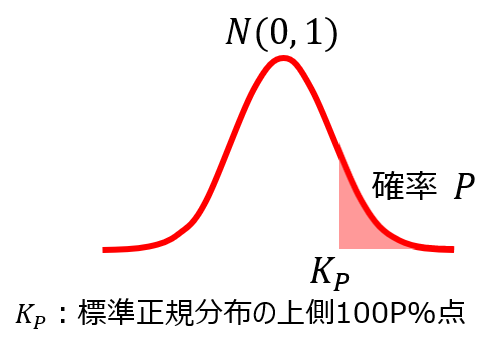
標準正規分布では、分布の横軸($Z$値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのNORM.S.DIST関数や標準正規分布表で簡単に求められます。
そして、この$Z$値を係数として用いることで、信頼区間の幅を計算することができるのです。
信頼度95%における母平均の信頼区間の計算式は、以下のように表されます。
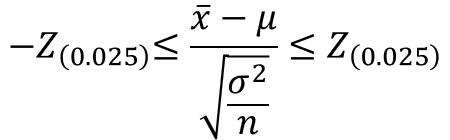
$μ$は母平均、$\bar{x}$は標本平均、$σ^{2}$は母分散、$n$はサンプルサイズを表します。
$Z$は標準正規分布の$Z$値を意味し、例えば信頼度95%の場合、$Z(0.025)=1.96$となります。
計算の手順
それでは、実際に母平均の区間推定をやってみましょう。
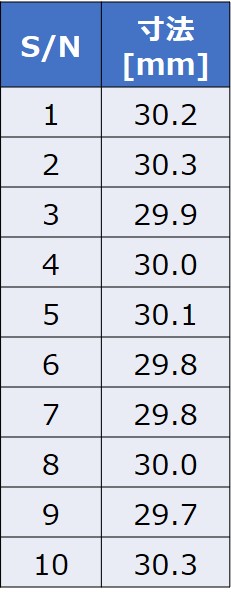
以下は、とある製品を無作為に10個抽出し、寸法を測定した結果です。
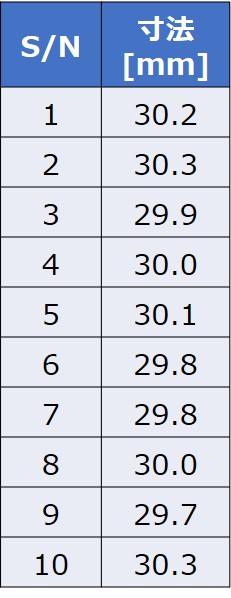
母分散が$σ^{2}=0.04$と分かっており、この製品の寸法の分布が正規分布に従うとするとき、母平均の95%信頼区間はいくらとなるでしょうか?
1.標本平均を求める
まず、抽出した標本(サンプル)の平均を算出します。
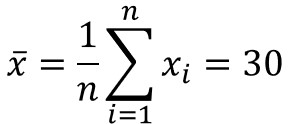
2.標本平均の標準化の式を使う
次に以下の式により、標本平均を標準化します。
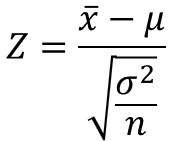
そして、次に示す標準正規分布表を用いて、信頼度に対応する$Z$値(表の符号でいうKp値)を求め、上式を$μ$について解くと信頼区間の境界値が得られます。
3.$Z$値を求める
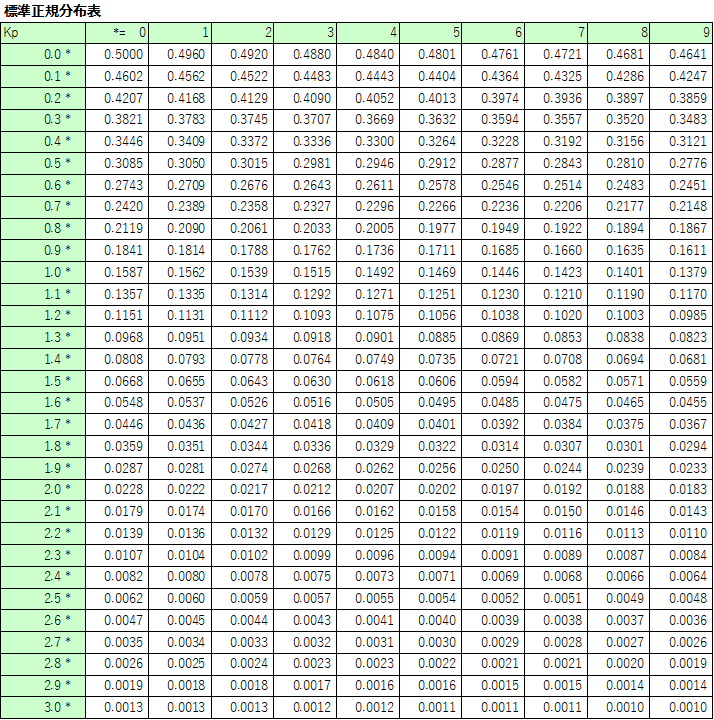
標準正規分布表を次に示します。
標準正規分布表では、Kp値に対し、小数点一桁までを縦軸、二桁目を横軸に表し、マトリックスの交差する箇所に対応する確率が記載されています。
今回の場合、求めたい信頼度は95%(0.95)となるので、確率Pが0.025(片側で2.5%)となるKp値を読み取ると1.96となります。
4.信頼区間を計算する
先ほどの式に信頼度95%の$Z$値を入れると、以下の不等式が成立します。
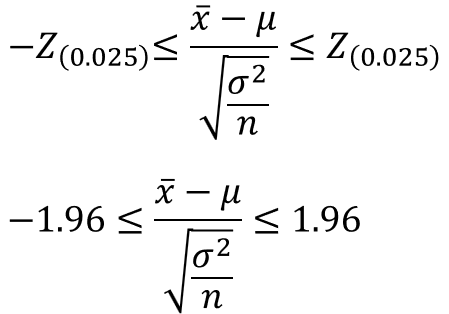
そして、これを$μ$に対して変換すると、次のようになります。
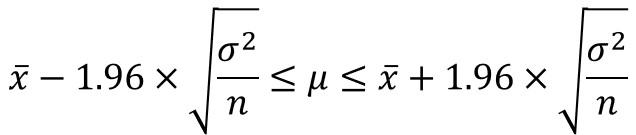
あとは、標本平均、母分散、サンプルサイズを代入すると、母平均の信頼区間を求めることができます。
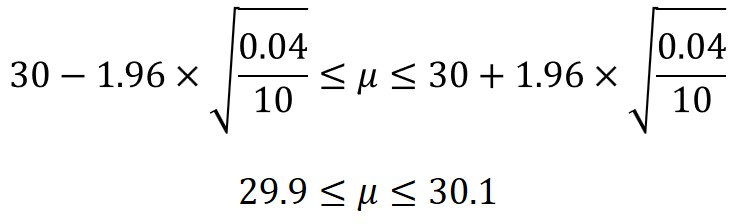

標本平均を中心に均等な範囲になるんだね
母分散が未知の場合
信頼区間の計算式
母分散が未知の場合、標本平均の分布はt分布に従います。
t分布とは以下の数式により求められる統計量t値が従う確率分布のことで、先ほどの標準正規分布の統計量と似ていますが、不偏分散を扱う点が異なります。
詳しくは以下の記事で解説していますので、合わせてご覧ください。

不偏分散とは、母分散が未知のときに標本データから求められる分散のことです。
標本分散と不偏分散は、それぞれ以下の式で計算できます。
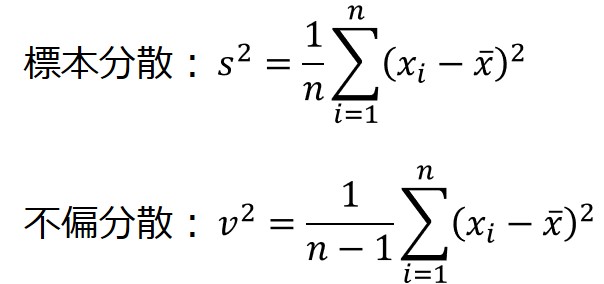
標本分散は、母集団の全データを測定できない性質上、どうしても母分散よりも、ばらつきを小さく見積もってしまう特性があり、不偏分散は、これを補正するためにサンプルサイズの係数をかけたものです。
不偏分散を用いることで、母分散が未知の場合でも母平均を推定することができるのです。
現実には、母平均が分からないのに母分散が分かっているケースはほとんどないので、こちらのケースの区間推定を用いる方が実用的と思います。
計算の手順
それでは、先ほどと同じ例題を使って、実際に区間推定をやってみましょう。
この製品の寸法の分布が正規分布に従うとするとき、母平均の95%信頼区間はいくらとなるでしょうか?
1.標本平均と不偏分散を求める
それぞれ、以下のように求められます。
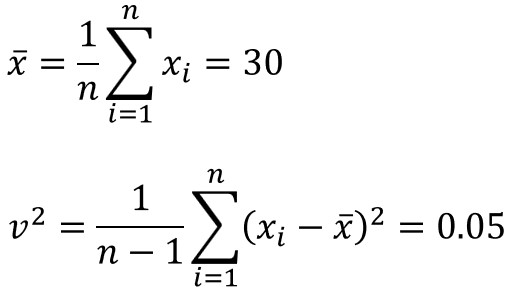
2.統計量tの式を使う
母分散未知の場合は、以下の統計量tを使います。
基本的な式の構成は、母分散既知の場合と同じなので覚えやすいですね。
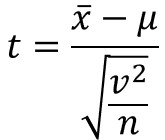
この統計量がt分布に従います。
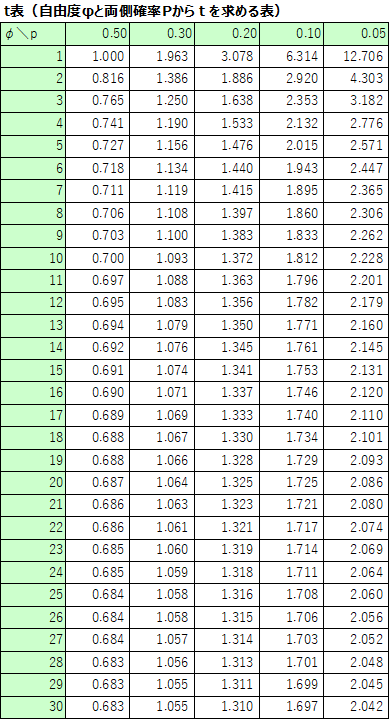
3.t分布表からt値を求める
t分布表とは、横軸に確率$p$、縦軸に自由度$φ$を取って、マトリックスの交差する箇所に対応するt値が記載されている表です。
t分布表で表す確率$p$は、t値に対する両側確率を意味します。
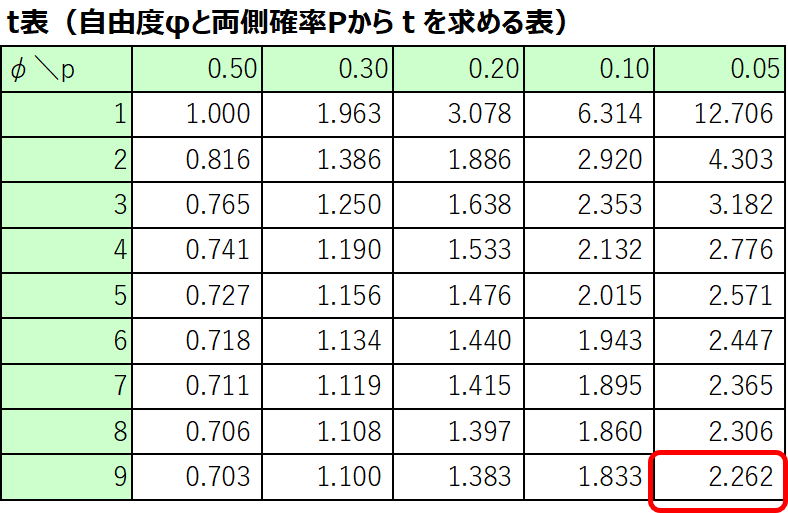
今回の場合、求めたい信頼度は95%(0.95)となるので、確率0.05に対応するt値を読み取ると、$t=2.262$と求めることができました。
4.信頼区間を計算する
母分散既知の場合と同じように、統計量tに対して以下の不等式が成立します。
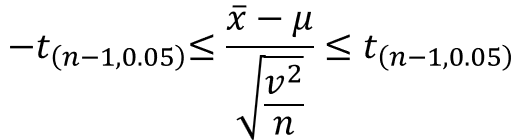
そして、これにtを代入して$μ$に対して変換すると、次のようになります。
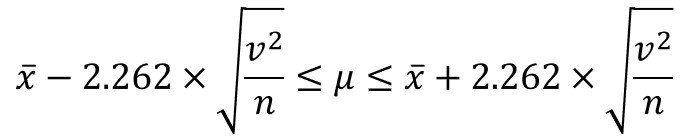
あとは、標本平均、不偏分散、サンプルサイズを代入すると、母平均の信頼区間を求めることができます。
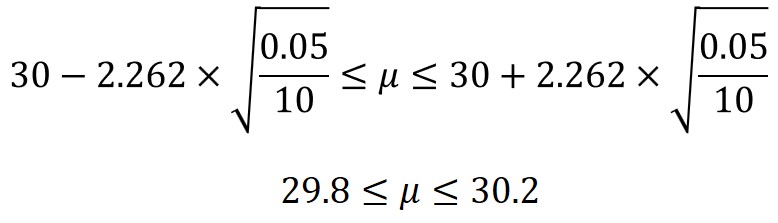
ここまでの計算結果を見てお気づきかもしれませんが、母分散が既知の場合よりも、母分散未知の方が信頼区間の幅が広い(推定の精度が低い)ことが分かります。
これは、不偏分散そのものが母分散を推定した値であるため、すでに不確かさが含まれていることを意味しているのです。

しっかり特徴を覚えておこう
中心極限定理との関係
中心極限定理とは、平均値$μ$、分散$σ^{2}$の確率分布から$n$個を抽出する際、標本平均$\bar{x}$は$n$が十分大きい場合において、 正規分布$N(μ,σ^{2}/n)$に従うという定理です。

つまり、サンプルサイズが無限大の場合、標本平均は母平均に収束することを表しています。
先ほどの区間推定の式からも分かる通り、サンプルサイズ $n$が無限大の場合、信頼区間の幅はゼロに近づくので、中心極限定理の定義の意味が分かっていただけると思います。
まとめ
- 母平均の信頼区間の求め方
⇒母分散既知:標準正規分布のZ値を用いる
母分散未知:t分布のt値を用いる - 計算の手順
⇒①:標本平均、不偏分散(母分散未知)を求める
②:統計量(Z値、t値)の式を使う
③:信頼度に対応する統計量を求める
④:母平均の推定値を計算する
母平均の推定は、区間推定の最も基本的なものの一つですので、しっかりと使えるようにしておきましょう。
最後までご覧いただきまして、ありがとうございました。




コメント