この記事では、分散比の信頼区間の計算方法、計算式の構成について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
分散比の信頼区間は、この記事で完結して解説していますが、標本調査の考え方など、区間推定(その1)の記事から段階を追って説明しています。
さまざまな区間推定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

F分布とは?
定義
分散比の信頼区間を求めるには、F分布を使います。
「F分布って聞いたことない」
「数式がむずかしすぎてサッパリ・・」
「聞いたことあるけど、何のために使うの?」
このような悩みや疑問をお持ちの方でも、心配する必要はありません。
F分布の「F」は統計学者フィッシャーに由来するもので、まさに母分散の比の区間推定や検定、分散分析を行うために用いられます。
確率密度関数は非常に複雑ですが、全く覚える必要はありません。
ほとんどの方にとっては、区間推定や検定に用いる統計量「F」の定義の式のみ覚えればよく、その式の構成も非常にシンプルです。
まずは概念だけ覚えておけば十分ですので、できるだけ簡単に順を追って説明しておきます。
F分布で用いるF値は以下の数式で定義されます。
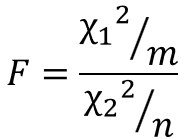
$χ^{2}$はカイ二乗値、$m$は第一自由度、$n$は第二自由度を表します。
まず、F分布を学習する前の予備知識として、カイ二乗分布を理解しておく必要がありますので、合わせてご覧ください。

カイ二乗分布は、標準正規分布を基にした確率変数の二乗和が従う確率分布です。
F分布とは、そのカイ二乗分布に従う2つの確率変数の二乗和をそれぞれの自由度で割って比で表したF値が従う確率分布のことを意味します。
何だか関係性が複雑な感じですが、F分布の元である2つのカイ二乗分布は、それぞれ正規分布に従うというのは、すなわち、2つの正規分布の分散の比を扱う場合にF分布を用いるということです。
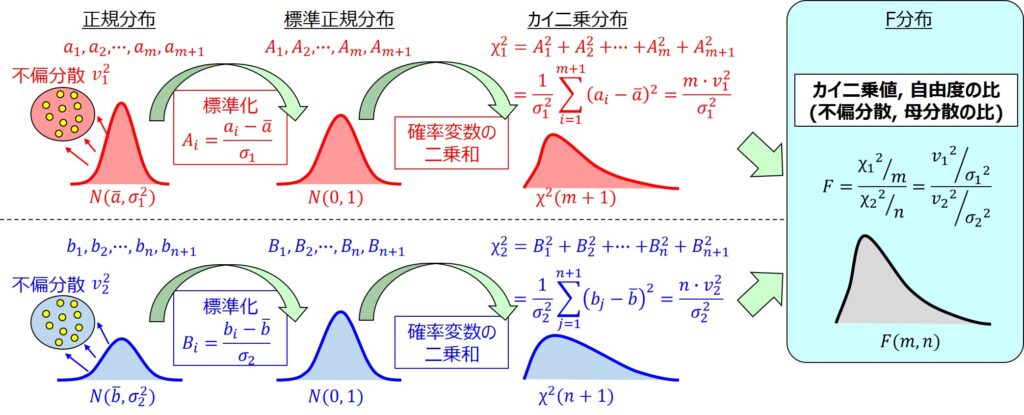

それぞれの分布とセットで繋がりを覚えておこう
F分布については、以下の記事で詳しく解説していますので、合わせてご覧ください。

F分布の特徴
区間推定や検定に使える便利な性質を紹介しておきます。
確率変数$X$が自由度$(m, n)$のF分布に従うとき、確率変数の逆数$1/X$は自由度$(n, m)$のF分布に従います。
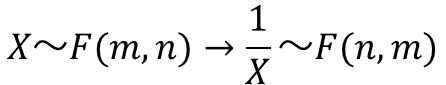
これは後ほど説明するF分布表を用いて上側(右側)確率を求める際に活用できる性質です。
F分布表では、一般的に5%や1%の上側確率に該当するF値が記載されています。
しかし、逆に95%や99%に該当する確率を求めたい場合には、これらの表から値をそのまま読み取るだけではいけません。
このような場合に上記の性質を用いれば、自由度を入れ替えて確率変数の逆数を取ることで、下側確率に変換できるのです。
分散比の信頼区間の求め方
信頼区間の計算式
F分布では、2つのカイ二乗分布の自由度と信頼度を設定すれば、全体の何%を占めているのか対応する確率が決まっており、エクセルのF.DIST関数やF分布表で簡単に求められます。
そして、このF値を係数として用いることで、信頼度○○%の信頼区間の幅を計算することができるのです。
分散比の95%信頼区間の計算式は、以下のように表されます。
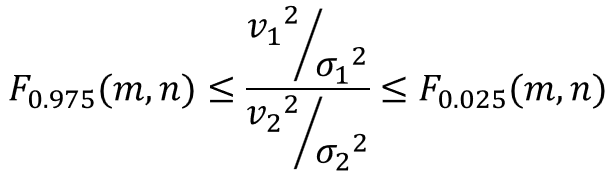
$σ_{1}^{2}$、$σ_{2}^{2}$は母分散、$v_{1}^{2}$、$v_{2}^{2}$は不偏分散、$m$は第一自由度、$n$は第二自由度を表します。
$F$はF値を意味し、例えば$m=9$、$n=9$、信頼度95%とした場合、$F_{0.025}(9, 9)=4.03$となります。
最終的には、この式を$σ_{1}^{2}$と$σ_{2}^{2}$の比率として不偏分散を移項し、母比率の信頼区間の比率を算出します。
この式をイメージで表すと以下のようになります。
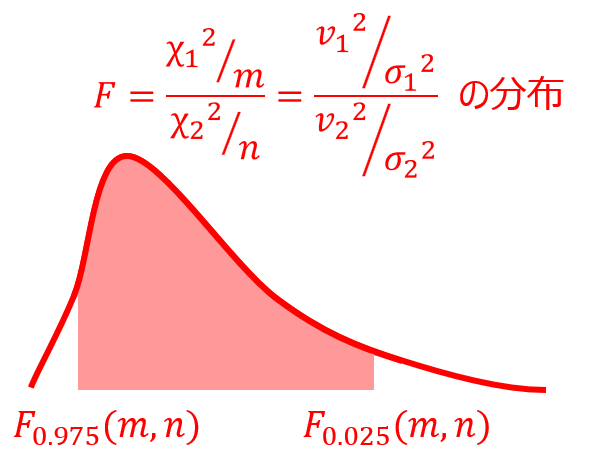
計算の手順
それでは、実際に分散比の区間推定をやってみましょう。
以下は、とある製品Aと製品Bを無作為に10個ずつ抽出し、寸法を測定した結果です。
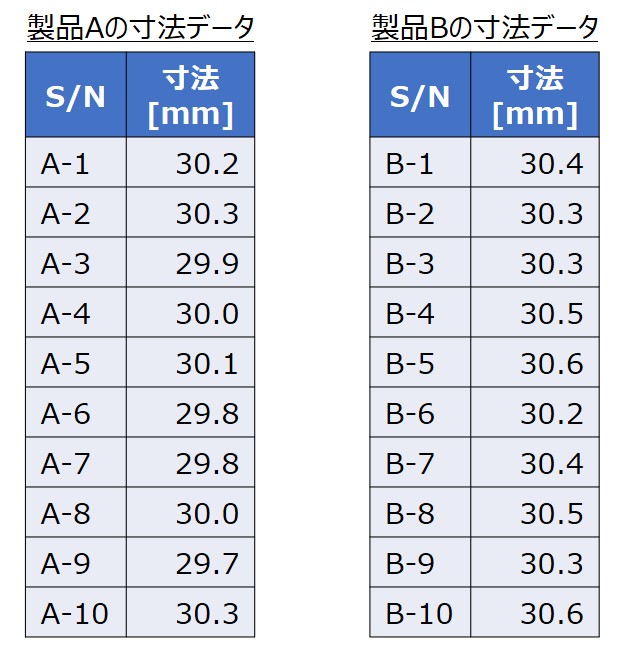
この製品Aと製品Bの寸法の分布が正規分布に従うとするとき、母分散の比の95%信頼区間はいくらとなるでしょうか?
1.不偏分散を求める
まずは標本のデータから不偏分散を計算します。
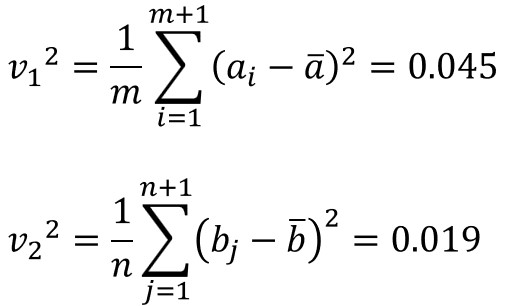
不偏分散と標本分散をうろ覚えの場合はこちらも参考にどうぞ。

2.F値を求める
次に信頼度に相当するF値をF分布表から求めます。
F分布表とは、横軸に第一自由度$m$、縦軸に第二自由度$n$を取って、マトリックスの交差する箇所に対応するF値が記載されている表です。
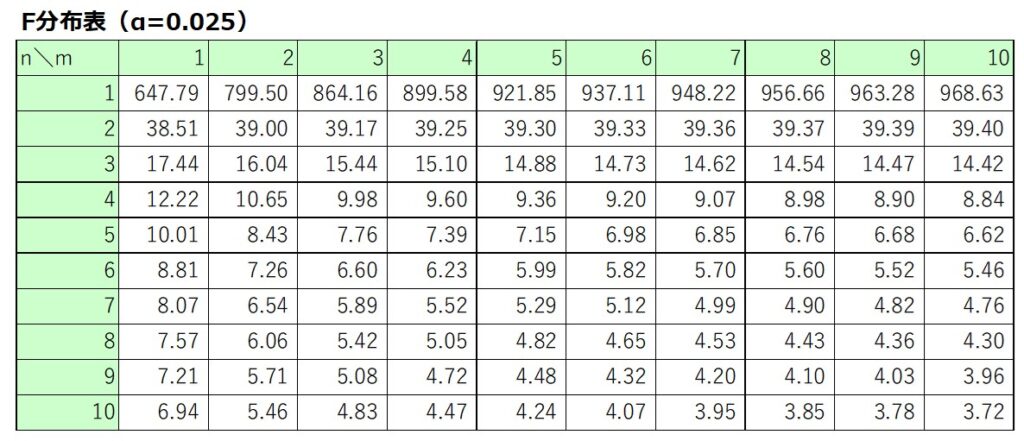
上側(右側)確率$α$の値によって対応するF値は異なるため、一般的に$α=0.05$、$0.025$、$0.01$に該当するF分布表が与えられています。
上側確率とは以下のようなイメージで、F値がとある値よりも大きくなる確率のことを表します。
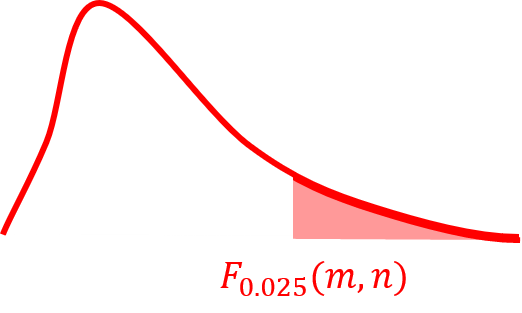
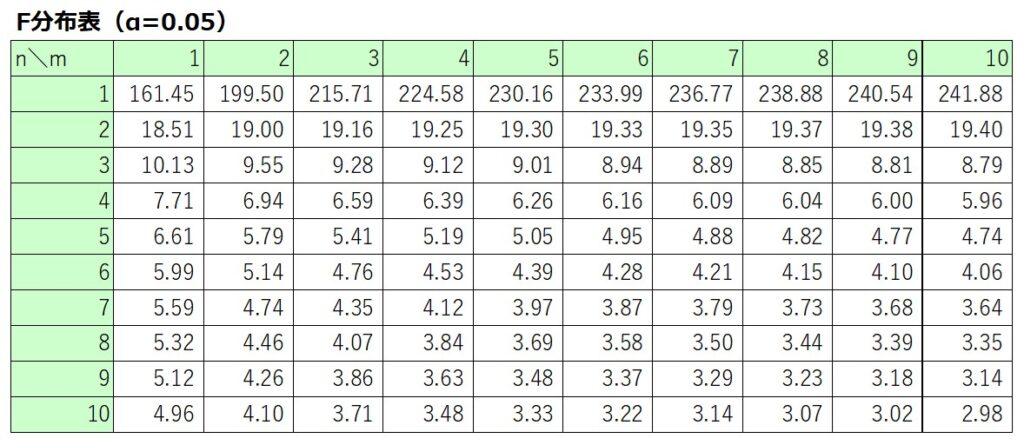
今回の区間推定では信頼度95%とすると、以下に示す片側2.5%のF分布表を用います。
そして、信頼度95%の上側確率にあたる第一自由度$m=9$、第二自由度$n=9$のF値は、$F_{0.025}(m, n)=4.03$と読み取ることができます。
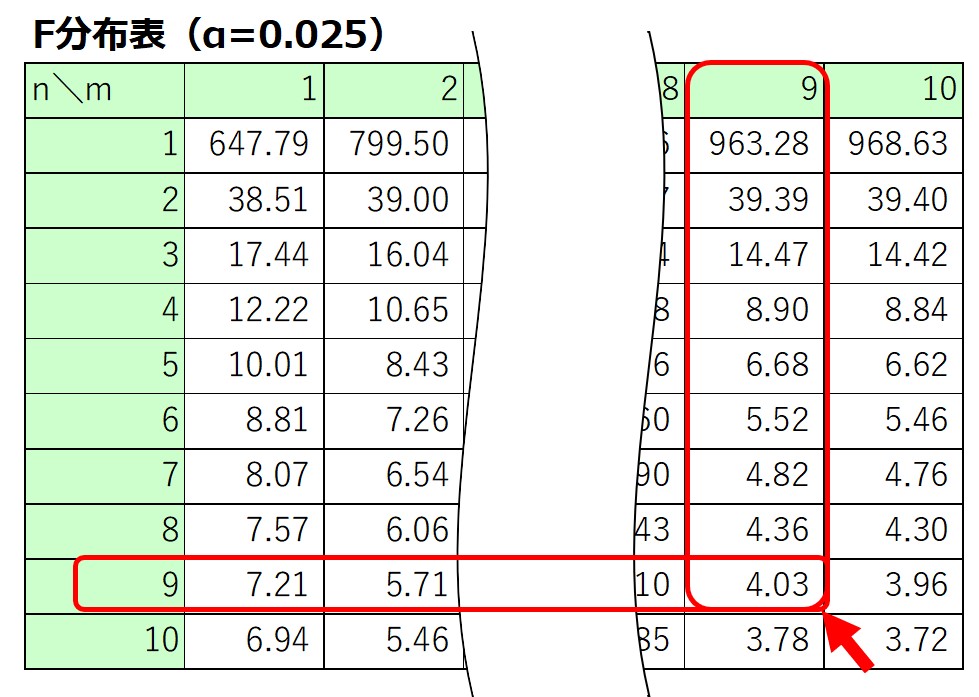
また、下側確率のF値は、$F_{0.975}(m, n)$ですが、先ほどのF分布表に該当する確率がありません。
ここで、先ほど説明した逆数のF分布の性質を活用するのです。
逆数の性質に当てはめると以下のように変換できます。
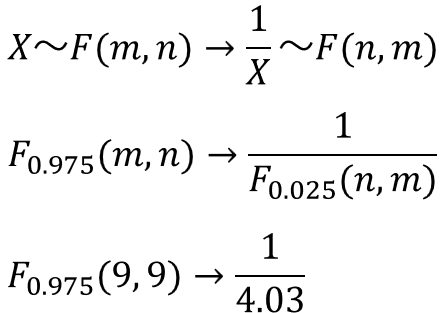
つまり、4.03の逆数ということで、$F_{0.975}(m, n)=1/F_{0.025}(n, m)=0.248$と簡単に求めることができました。

2つの分布の比率だから逆数を取ればいいんだね
ちなみに、エクセルではF.INV.RT関数を用いることで、対応するF値を求められます。
F.INV.RT関数とは、F分布の上側確率の逆関数を表し、今回の事例の場合、$=F.INV.RT(0.975, 9, 9)=0.248$と信頼度と自由度を設定するだけで同じ結果が得られます。
3.信頼区間を計算する
区間推定の定義の式に信頼区間95%のF値を入れると、以下の不等式が成立します。
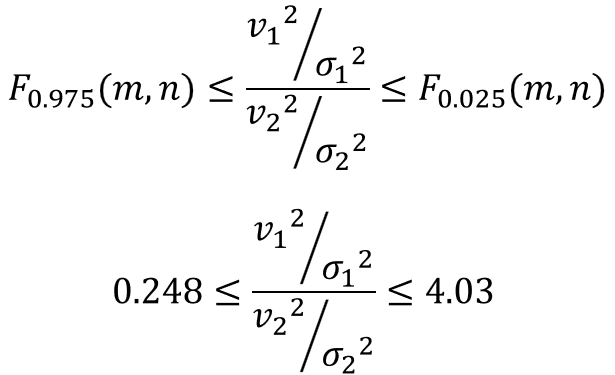
そして、これを$σ_{2}^{2}/σ_{1}^{2}$に対して変換すると、次のようになります。
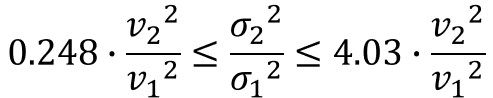
あとは、不偏分散の計算結果を代入すると、母分散の比の信頼区間を求めることができます。
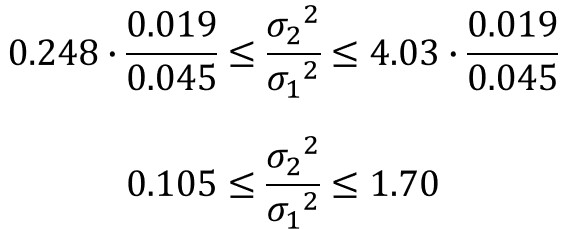
まとめ
- 母分散の比の信頼区間の求め方
⇒F分布を用いる - 計算の手順
⇒①:不偏分散を求める
②:信頼度に対応するF値を求める
③:分散比の推定値を計算する
最後まで読んでいただき、ありがとうございました。




コメント