仮説検定の考え方、帰無仮説・対立仮説を基礎から理解しよう　～統計的検定（その1）～

「統計的検定って何だかむずかしそう」
「登場する専門用語が多くてサッパリ・・」
「どのような手順と考え方で検定するの？」

このような疑問や悩みをお持ちの方に向けた記事です。

統計的検定とは、母集団に関して立てたとある仮説が成立するか否か、背理法の考え方を用いて標本データから確率論的に結論を導き出す手法のことです。

標本調査を行う中で、検定という言葉を一度は耳にしたことのある方も多いかもしれませんが、聞きなれない専門用語ばかりで一から勉強する気力がなくなりますよね。

この記事では、統計的検定の概念とメリット、登場する用語の意味、検定の大まかな手順について解説しますので、皆さんの参考になればうれしいです。

統計的検定とは？

定義

まずは、統計的検定の定義を確認してみましょう。

統計的検定：統計学で、母集団から抽出した標本が、母集団全体を説明する統計的仮説を支持するかを判定すること。実際に観測された標本が、ある仮説に従う母数または確率分布をもつ母集団から抽出される確率を求め、有意水準と比較して仮説の当否を判断する。統計的仮説検定。検定。

引用元：デジタル大辞泉（小学館）

さっそく難解な用語がたくさん登場して、この段階で諦めてしまいそうですね・・。

簡略化すると、母集団に関して立てたとある仮説が成立するか否か、標本データから確率論的に結論を導き出すということです。

「仮説」というと、推理小説に登場するような「犯人は○○に違いない！」といったものが思い浮かんだかもしれません。

本質的な意味は同じですが、ここで言う仮説は「統計的仮説」で、例えば「$\bar{μ}＝μ_{o}, \bar{μ}＞μ_{o}$」といった数式で表現されます。

基本的な考え方

統計的検定の概念について、実際の題材の例を交えて少し噛み砕いて捉えてみましょう。

※具体的な数値を入れての計算方法は個別の記事であらためて解説しますので、ここでは題材の例だけ挙げて説明します。

まず、検定を行う動機として、工程改善後の製品の強度が高くなったことを示したい、という目的が挙げられます。

しかしこの時、母集団の全ての個体、すなわち全ての製品に対して強度データを取ることは現実的な運用ではありません。

そもそも、強度測定のような破壊試験では全数調査を行うことができず、標本調査の結果から母集団の状態を推定するしかないのです。

そこで、母集団に対して一つの仮説、今回のケースでは「改善後の強度の平均値は$μ_{o}$である（改善前後で製品の強度は同じ）」という仮説を立てます。

この仮説に対して、標本調査の結果から算出した指標（検定統計量）が確率的に通常起こり得る範囲なのか、稀な事象なのか、比較することで効果の有無を判定するのです。

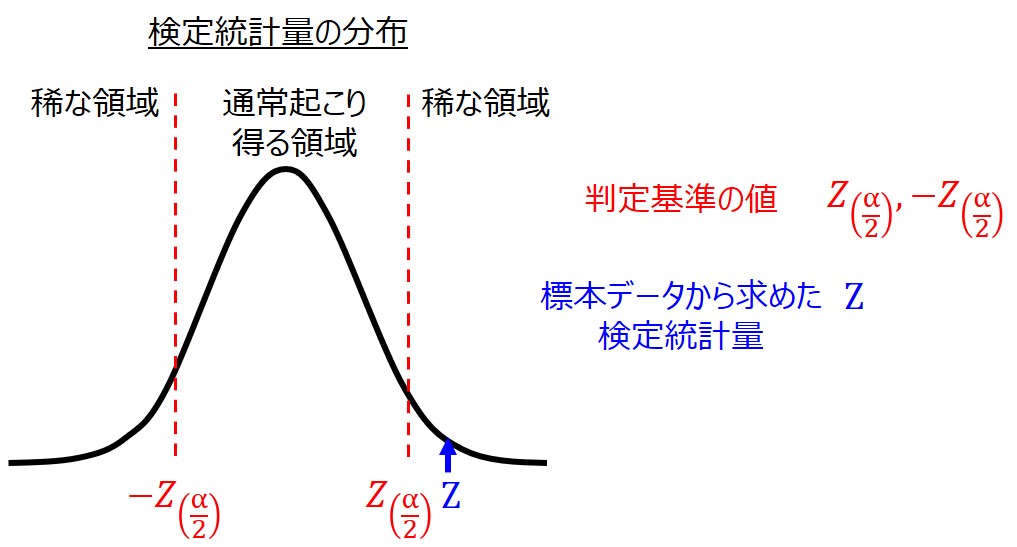
例えば、改善後の平均値が$μ_{o}$となる事象が頻繁に起こり得るのであれば、改善したとは言えないと判断します。

反対に$μ_{o}$となるのが稀な事象なのであれば、改善後の標本データは改善前の母集団と同じではない、つまり工程改善の効果があったと判断できるわけです。

検定の確からしさ

確率の世界では、基本的に絶対という表現は用いられません。

先ほどの例で言うと、改善後の強度が改善前の平均値$μ_{o}$と同じになる確率は極めて低かったとしても、絶対に起こり得ないとは言い切れません。

しかし、完璧な結論を求めていては、先ほどにも述べたように全数調査をする他にないのです。

そのため、統計的検定では「確からしさ」の概念と合わせて考える必要があり、一般的には、信頼度95%、または99%が用いられます。

例えば、信頼度99%の場合、99%の確率で平均値の差の有無を正しく判定できたと解釈します。

逆に言うと、本当は差がないのに差があると判断してしまう場合など、1%の確率で間違った結論にたどり着くリスクがあるということで、この性質をきちんと理解しておきましょう。

仮説の表現のしかた

ここで、仮説の表現のしかたについて触れておきます。

元々、平均値に差があることを示したいのに、なぜ「平均値が同じ」ことを仮説にするのか、わざわざ回りくどい言い方をするのか、疑問に思うかもしれません。

これには背理法と呼ばれる証明方法を用いています。

背理法とは、証明したい命題に対して、いったん命題が正しくないと仮定し、その場合に矛盾が生じることを導き出すことで命題が成り立つことを証明する手法です。

統計的検定において「矛盾」とは、頻繁に起こり得る事象ではない（＝稀な事象である）ことを意味します。

なぜ背理法を用いる必要があるのかというと、「平均値に差があることを証明する」ことが非常に難しいからです。

「証明する」ためには、結局のところ全てを調べるしかなく、標本調査の目的から考えて本末転倒になってしまいます。

それでは、「平均値に差がないと仮定した場合の矛盾を証明する」場合ならどうでしょうか？

矛盾を証明する場合、反例を見つければよく、例えば、標本調査の結果がその反例であることを示せば、仮説を否定することができます。

そのため、標本調査の結果から、平均値が同じとは言えないことを導き出すことが、統計的検定で期待している結論になるのです。

検定を行うメリット

統計的検定を行うことのメリットを3つ紹介します。

１．標本から全体を推測できる

これまでにも述べたように、母集団に関する仮説の真否を誤りなく調べるためには、集団の個体を全て調べる全数調査を行うしかなく、膨大な労力と時間を費やすことになります。

しかし、そもそも寸分の狂いもない絶対的な検定が必要なケースは、普段の仕事や日常生活でそれほど多く出くわすでしょうか？

95%または99%の確率で仮説の真否を判断できれば十分なことも多く、このように費用対効果を踏まえて、効率的な判断を下すために統計的検定が用いられるのです。

２．定量的な基準で判定できる

統計的検定では、標本データをもとに算出した検定統計量を基準に母集団との差の有無を判断します。

検定統計量は基本的に平均や分散などの統計量をもとに決められた計算式で算出され、あらかじめ検定統計量の値に対応する発生確率が決まっています。

そのため、個人の主観やその時々によって判定基準が変わることはなく、常に客観的で定量的な判定を下せることがメリットと言えます。

３．目標値を明確にできる

検定の結果、○○%の確率で母集団と差異がある、または同じとは言えないといった結論が得られます。

これを単なる言語的な結論と捉えることもできますが、例えば平均値や分散をいくつにすれば期待した結論を導き出せるか、今後の改善活動の目標値を見つけることにも活用できます。

検定に登場する用語

統計的検定を行うにあたり、登場する用語の意味を説明します。

いずれも、用語の定義を正しく理解できていないと、間違った数値を引用したり、異なる結論にたどり着いたりする可能性もあるので、注意が必要です。

帰無仮説，対立仮説

帰無仮説：統計学の仮説検定において、その当否が検定される仮説。通常、否定されることを前提として立てられ、この仮説が棄却されると対立仮説が成立する。

引用元：デジタル大辞泉（小学館）

つまり、無に帰することを期待した仮説という意味で帰無仮説と呼ばれ、$H_{0}$と表記されます。

検定を行う上では、まず最初に帰無仮説を設定するところから始めます。

例えば、標本データ$\bar{μ}$と母集団$μ_{o}$の平均値が等しいと仮定する場合、「$H_{0}：\bar{μ}=μ_{o}$」を帰無仮説に設定します。

一方で対立仮説$H_{1}$とは、検定統計量が一定の範囲内に収まらない（＝帰無仮説が棄却された）場合に採択されるもので、調べたい本来の目的の仮説のことです。

例えば、上記の$H_{0}$に対する対立仮説は、「$H_{1}：\bar{μ}≠μ_{o}$」と設定します。

この場合、「標本データと母集団の平均値が等しいとは言えない」ことが対立仮説となります。

また、対立仮説は上記の一通りに決まるわけではなく、「$H_{1}：\bar{μ}<μ_{o}$」と設定する場合もあります。

この場合、「標本データの平均値は母平均よりも小さい」ことを表し、例えば不良率の改善など低減効果を期待した検定を行うケースで用いられます。

もちろん、今回の題材で紹介した強度データのように「$H_{1}：\bar{μ}>μ_{o}$」と設定するケースもあり、目的に応じて適切な対立仮説を設定するようにしましょう。

検定統計量

検定統計量とは、帰無仮説の棄却/採択の判定基準となる指標のことで、標準正規分布やｔ分布などから検定統計量に対応する発生確率を求めることができます。

例えば、母分散が既知の場合、以下に示す検定統計量$z$は標準正規分布$N(0,1)$に従います。

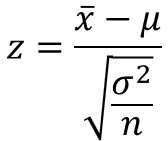
$\bar{x}$は標本の平均値、$μ$は母平均、$σ^{2}$は母分散、$n$はサンプルサイズを表します。

つまり、これらの値を代入して$z$を求めることで、対応する発生確率に変換することができるのです。

第一種の誤り，有意水準

第一種の誤りは、あわて者の誤りとも呼ばれ、本当は誤りでないのに誤りと誤判定してしまうことです。

工程管理や抜取検査でも良く用いられる考え方ですが、統計的検定の場合では、本当は帰無仮説が正しいのに、誤って棄却してしまうことを意味します。

第一種の誤りにあたる確率は$α$と表記され、この$α$の値のことを有意水準と呼びます。

第二種の誤り，検出力

第二種の誤りは、ぼんやり者の誤りとも呼ばれ、本当は誤りであることを見逃して正しいものと誤判定してしまうことです。

統計的検定では、本当は帰無仮説が誤りで棄却すべきところを、見逃して帰無仮説を採択してしまうことを意味します。

第二種の誤りにあたる確率は$β$と表記されます。

このとき、$1-β$は帰無仮説の誤りを見逃さずに正しく棄却できる確率を表し、この$1-β$の値のことを検出力と呼びます。

両側検定

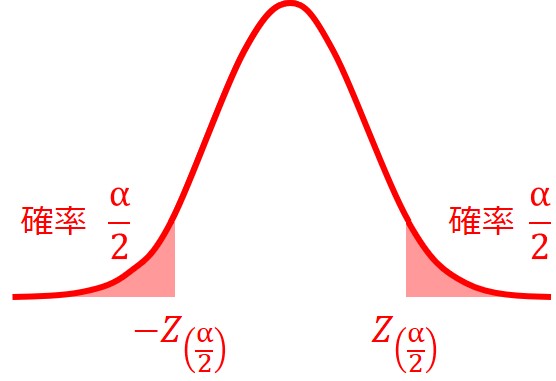
両側検定とは、確率分布の両側に棄却域を設ける考え方の検定です。

標本から求めた検定統計量が、分布に対して大き過ぎても小さ過ぎても帰無仮説が棄却されます。

両側検定の場合、例えば「$H_{0}$：平均値が等しい」という帰無仮説に対し、「$H_{1}$：平均値は等しくない（差がある）」という対立仮説になります。

大きい場合も小さい場合も含めて「等しくない」という意味で、有意水準$α$は$α/2$ずつ両サイドに分かれて棄却域が設けられます。

片側検定

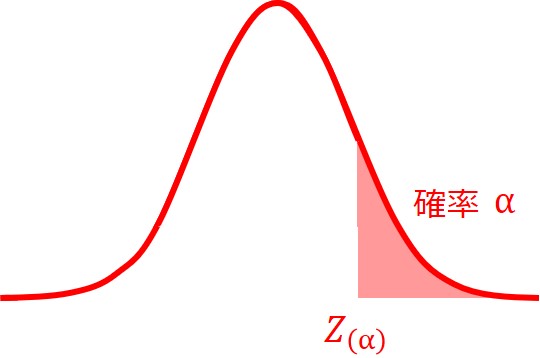
確率分布の片側に棄却域を設ける考え方の検定です。

片側検定では、分布に対して大き過ぎる、または小さ過ぎるといったように、どちらか片方に対する検定を行います。

そのため、対立仮説は「$H_{1}$：平均値は大きくなったと言える」といったように、両側検定と設定のしかたが異なるので、間違えないようにしましょう。

また、有意水準$α$は片側のみに当てはめられて棄却域が設けられます。

そのため、有意水準が同じ95%の場合でも、両側2.5%ずつなのか、片側のみ5%なのかによって、検定統計量の判定値が変わるので注意が必要です。

P値

Probability（確率）の頭文字が名前の由来となっており、検定統計量がその値となる場合の確率を表します。

例えば、自由度10のｔ分布に従う検定統計量ｔ=1.812とすると、片側検定におけるP値は0.05となります。

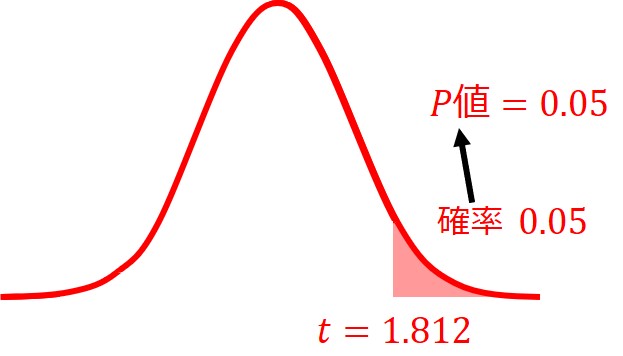
しかし、同じｔ=1.812の値でも、両側検定のP値は0.1となります。

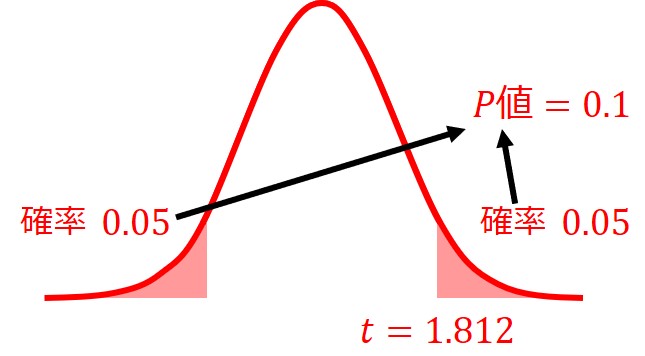
このP値は、ｔ分布表から大よその値を読み取ることもできますが、ｔ分布表は自由度と確率に対応したｔ値の表なので、P=0.05や0.1のような区切りの良い点以外は正確な数値を求められません。

しかし、エクセルであれば、片側検定ならT.DIST.RT関数、両側検定ならT.DIST.2T関数を使ってP値を簡単に求めることができるので、ぜひ覚えておきましょう。

検定の手順

ここまで検定の考え方や用語について説明しましたが、最後に検定の手順を整理しておきます。

具体的な数値の計算については、エクセルの分析ツールを用いれば、必要な統計量の計算を一瞬で行うことができます。

計算手順に関しては、分析ツールの使い方と合わせて個別の記事で解説しますので、合わせてご覧ください。

１．仮説を設定する

帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。

帰無仮説には、棄却されることを期待した、本来調べたい効果と反対の事象を設定します。

対立仮説には、本来調べたい事象の仮説を設定します。

両側検定と片側検定の違いに注意して、差異があることを示したいのか、大きい（または小さい）ことを示したいのか、目的に沿った適切な仮説を設定しましょう。

２．検定統計量を算出する

標本調査の結果から、検定統計量を計算します。

母分散が既知の場合、未知の場合、平均値に関する検定や不適合比率に関する検定など、さまざまな分類がありますので、目的に合った検定統計量を求めましょう。

３．帰無仮説の棄却/採択を判定する

検定統計量に対応する確率の値から、帰無仮説$H_{0}$の棄却（$H_{1}$の採択）または$H_{0}$の採択を判定します。

信頼度は95%、または99%を基準として用いることが多く、すなわち有意水準$α$は$α=0.05$または$α=0.01$を判定基準とします。

４．検定の結論を導く

判定結果から、検定の結論を導き出します。

元々の検定の目的に立ち返り、「平均値に差があるとは言えない」、または「有意水準○○%で平均値に差があると言える」といった結論を出します。

$α=0.01$の場合は、「高度に有意」と表現することもあります。

まとめ

• 統計的検定
  ⇒母集団に関して立てたとある仮説が成立するか否か、背理法の考え方を用いて標本データから確率論的に結論を導き出す検定のこと
• 検定を行うメリット
  ⇒標本から全体を推測できる
  　定量的な基準で判定できる
  　目標値を明確にできる
• 検定に登場する用語
  ⇒帰無仮説、対立仮説
  　検定統計量
  　第一種の誤り、有意水準
  　第二種の誤り、検出力
  　両側検定、片側検定
  　P値
• 検定の手順
  ⇒１．仮説を設定する
  　２．検定統計量を算出する
  　３．帰無仮説の棄却/採択を判定する
  　４．検定の結論を導く

最後まで読んでいただき、ありがとうございました。