「条件付きとはどういうものか?」
「とにかく色んな例題でイメージを掴みたい」
「乗法定理との違い、見分け方を知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
条件付き確率とは、事象Aが起きたもとで、事象Bが起きる確率のことを表します。
日常生活では単一の事象で片づけられる確率論ばかりではなく、2つあるいはそれ以上の事象が複合的に起こるケースが多くあります。
この記事では、条件付き確率の意味と公式、乗法定理の公式と見分け方について、日常的な題材の例を交えて解説しています。
「条件付き」と堅苦しく表現すると身構えがちですが、むずかしい計算は不要です。
解き方のコツを掴めるよう、できるだけ例題と図解を交えて記載しましたので、ぜひ最後まで読んで参考にしていただければと思います。
条件付き確率とは?
条件付き確率とは、事象Aが起きたもとで事象Bが起きる確率のことで、$P(B\mid{A})$または$P_{A}(B)$と記載されます。
条件付き確率の公式は以下のようになります。
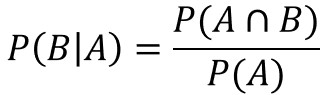
$P(A\bigcap{B})$は事象AとBがともに起きる確率、$P(A)$は事象Aが起こる確率を表します。
ベン図で表現するとイメージが掴みやすいと思います。
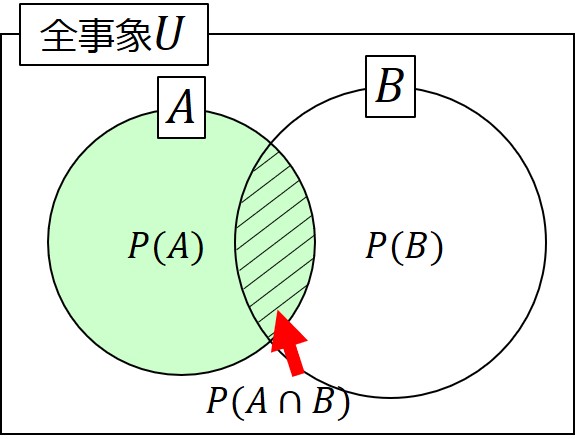
条件付き確率で登場するのは、色付きの領域$P(A)$とハッチングの領域$P(A\bigcap{B})$で示す確率です。

図で見ると意外とシンプルなんだ
例題
さて、条件付き確率の定義と概念が分かったところで、これでバッチリ完璧に使いこなせそう、という方は少ないのではないでしょうか。
私自身も定義や公式だけでは全くイメージが掴めず、事象Aと事象Bっていったい何?といった漠然とした疑問が残り、はっきりと理解できたとは言えない状態でした。
やはり、実際の具体例でみないと、理解が進みませんね。
代表的な例題をいくつか紹介します。
直感的なイメージと合わない答えも多く、パラドックスの感覚がとても面白いので、いっしょに考えながら見ていきましょう。
例題1:男の子?女の子?
男女の生まれる比率が等しく$\frac{1}{2}$であるとします。Aさんには二人の子供がいます。そのうち一人は男の子であると知りました。さて、もう一人の子供が男の子である確率はいくつでしょうか?
まず直感でどのような確率を思い浮かべたでしょうか?
男の子の生まれる確率は$\frac{1}{2}$だから、$\frac{1}{2}$に決まってるでしょ?と思った方・・私もそうです。
一人の性別が分かったところで、もう一人の性別を決める要因にはならないし、$\frac{1}{2}$以外考えられない、という感覚でした。
しかし実は、答えは$\frac{1}{3}$になります。
なぜ、このような結果になるのか、解説していきます。
解説
基本に立ち返って、全通りのパターンを考えてみると分かりやすくなります。
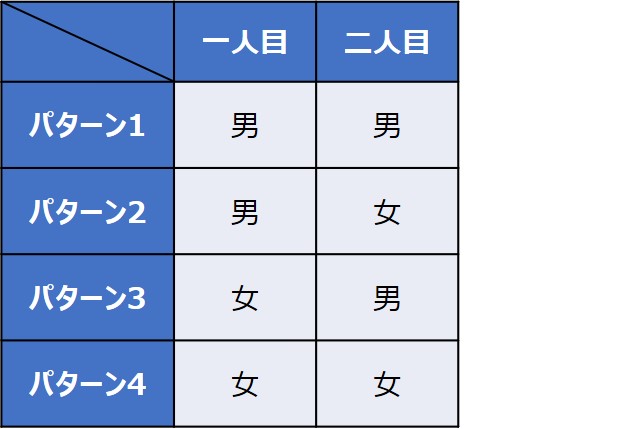
どの組み合わせも等しく$\frac{1}{4}$になります。
ここで、子供のうちの一人が男の子となる組み合わせは3パターンあります。
すると、その3つのうち、もう一人の子供が男の子である組み合わせは、1パターンのみということになります。
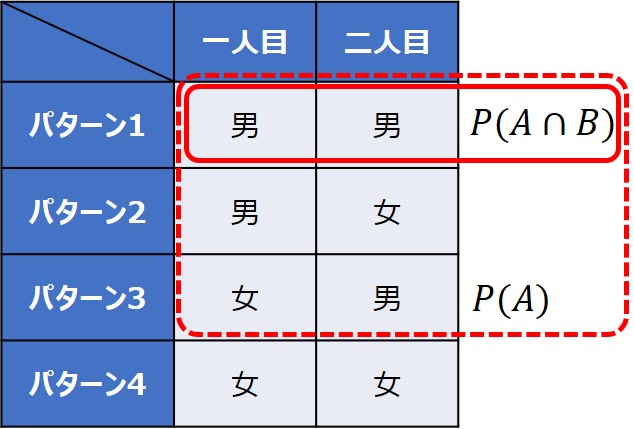
つまり、「子供の一人が男」という前提付きの条件下では、組み合わせ数は3パターンに絞られ、その中で「もう一人が男」になるのは1つとなり、$\frac{1}{3}$という結果になるのです。
これを条件付き確率の公式で求めてみましょう。
$P(B\mid{A})$:子供の一人が男の子という条件下で、もう一人も男である確率
$P(A\bigcap{B})$:二人とも男の子である確率
$P(A)$:少なくとも一人は男の子である確率
これを解くと以下の通り、同じ結果が得られます。
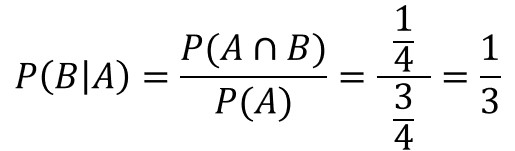
例題2:陽性になる確率は?
1万人に1人の割合で罹患する病気があったとします。この病気の陽性/陰性を判定する検査において、誤判定する割合が1%とします。Aさんが陽性と判定されたとき、本当に病気にかかっている確率はいくつでしょうか?
先ほどと同じように、まず直感で考えてみましょう。
誤判定率が1%ということは、病気でないのに陽性と判定される確率が1%ということです。
「陽性と判定されたということは、その逆で99%だ」と考えた方・・よくある誤りです(同じくまた私も引っかかりました)。
これには、1万人に1人の割合で病気にかかるという条件が抜けているのです。
解説
組み合わせを表にしてみましょう。
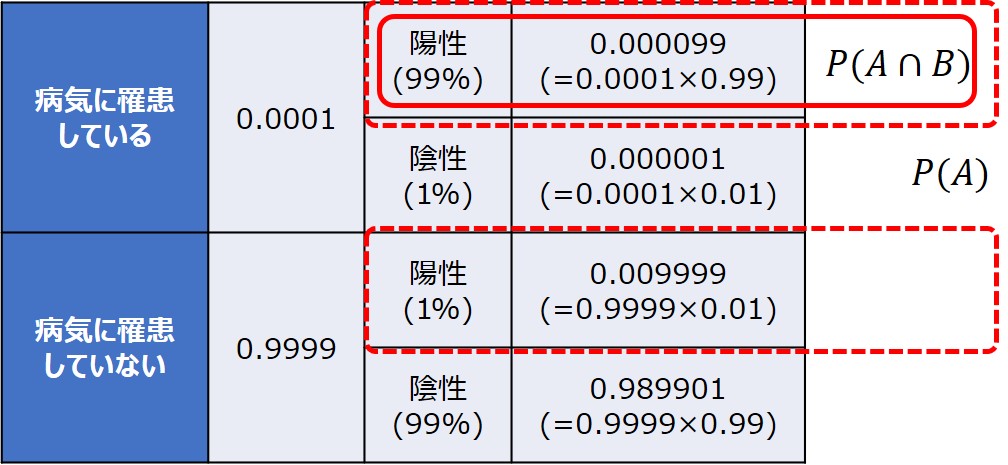
$P(A\bigcap{B})$:陽性かつ病気に罹患する確率
$P(A)$:陽性になる確率
$P(A\bigcap{B})$は、$0.0001×0.99=0.000099$となります。
$P(A)$は、実際に病気であって正しく陽性と判定される場合と、実際には病気でないのに誤って陽性と判定される場合があります。
これを計算すると以下のようになります。
$P(A)=0.0001×0.99+0.9999×0.01$
$=0.010098$
つまり、$P(B\mid{A})$( 陽性と判定されたときに病気である確率 )は以下の通り。
$P(B\mid{A})=0.000099÷0.010098$
$=0.0098$
答えは$0.98$%なのです。
陽性と判定されたのに、実際に病気である確率が$0.98$%というのは感覚と合わない気がしますが、そもそも病気になる確率が低いことを考えると、真実はこの程度ということです。
例題3:サイコロ
さて、ここからは、試験問題などでよく登場する題材を紹介します。
出る目が均等な確率のサイコロを2回振り、最初に出た目が3であったとします。この時、2回振った目の合計が7以上となる確率はいくつでしょうか?
解説
$P(A\bigcap{B})$:最初の目が3、かつ目の合計が7以上の確率
$P(A)$:最初に出た目が3である確率
$P(A)=\frac{1}{6}$と簡単に求められます。
$P(A\bigcap{B})$に当てはまるのは、(3,4)(3,5)(3,6)の3通りです。
出る目の通り数は全部で36ですから、$P(A\bigcap{B})=\frac{3}{36}=\frac{1}{12}$となります。
すなわち、以下となります。
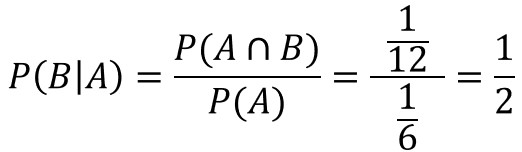
例題4:袋に入った2色の玉
袋の中に赤玉と白玉が5つずつ入っていて、玉を元に戻さないで次の玉を取り出すことを3回実施したとします。2回目と3回目に取り出したのが赤玉と分かっているとき、1回目に取り出した玉も赤玉である確率はいくつでしょうか?
解説
この問題は、条件付き確率が当てはまることを見落としがちな例です。
というのも、2回目と3回目に取り出す玉は、時系列では1回目より後の話なので、一見、1回目に出る玉の色に影響を及ぼさないように思うからです。
しかし、例えば赤玉と白玉が5個ずつではなくて、赤玉が2個、白が8個だとしたらどうでしょう。
2回目と3回目が赤と決まっていたら、必然的に1回目は白になります。
つまり、1回目が赤の確率はゼロで、決して独立した事象の確率$\frac{2}{8}$ではありません。
このことから、時系列が前後していても、条件付き確率の考え方が当てはまることを意識して覚えておきましょう。
さて、話を戻すと、以下の確率を求めることになります。
$P(A\bigcap{B})$:1回目から3回目が全て赤玉の確率
$P(A)$:2回目と3回目が赤玉である確率
$P(A\bigcap{B})=\frac{5}{10} × \frac{4}{9} × \frac{3}{8}= \frac{1}{12}$
$P(A)=(赤・赤・赤)+(白・赤・赤)$
$= \frac{5}{10} × \frac{4}{9} × \frac{3}{8} + \frac{5}{10} × \frac{5}{9} × \frac{4}{8} $
$= \frac{1}{12} + \frac{5}{36} = \frac{2}{9}$
すなわち、以下となります。
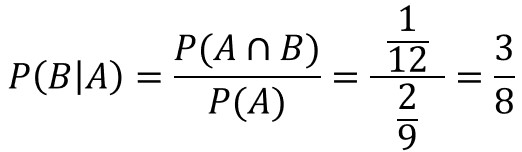
乗法定理とは?
公式と見分け方
乗法定理は、条件付き確率の式を変換したもので、以下の通り定義されます。
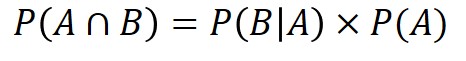
式の見た目の通り、「事象Aと事象Bが同時に起こる確率」を求めたい場合に使う定理です。
試験問題などで、条件付き確率の公式を使うのか、乗法定理の公式を使うのか、混乱してしまうことがあると思います。
ここで焦らず、問題文に注目してみてください。
条件付き確率では、「・・・であるとき、・・・となる確率」という表現や意味が含まれているはずです。
先ほどの例題を振り返ってみても、この文脈に合致していると思います。
これに対し、乗法定理では「・・・と・・・が同時に起こる確率」となっています。
問題文をサラッと読むと見落としがちですが、意識して読めばどちらの公式を使えば良いのか簡単に判別できるので、その後が非常に考えやすくなります。
例題5:袋に入った2色の玉
袋の中に赤玉と白玉が5つずつ入っていて、玉を元に戻さないで玉を2個取り出すとします。どちらも赤玉となる確率はいくつでしょうか?
解説
$P(A)$:1回目が赤玉である確率
$P(B\mid{A})$:1回目に赤玉が出た後に2回目に赤玉が出る確率
2回目の玉を引く時点では、残り9個、赤玉4個であることから
$P(B\mid{A})=\frac{4}{9}$
すなわち、以下となります。
$P(A\bigcap{B})=\frac{5}{10}× \frac{4}{9}= \frac{2}{9}$

どっちの公式もバッチリだね
まとめ
- 条件付き確率
⇒事象Aが起きたもとで、事象Bが起きる確率のこと
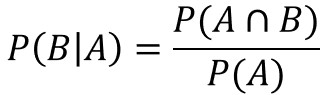
- 乗法定理
⇒条件付き確率の式を変換したもの
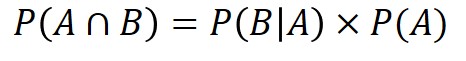
- 見分け方
⇒条件付き確率「・・・であるとき、・・・となる確率」
乗法定理「・・・と・・・が同時に起こる確率」
直感とずれた結果に驚いた方も多かったのではないでしょうか。
丸暗記しておけば良しという訳ではありませんが、条件付き確率や乗法定理の公式は、こういった感覚とのずれに惑わされないための有効なツールです。
ぜひ、身近な題材で試してみてください。





コメント