「モンティ・ホール問題って聞いたことない」
「どんな確率の知識が役に立つの?」
「感覚的に理解するポイントを教えてほしい」
このような疑問や悩みをお持ちの方に向けた記事です。
モンティ・ホール問題とは、実際にアメリカのテレビ番組で行われた景品当てゲームの問題のことです。
問題そのものは中学生にも理解できる簡単なものですが、直感と答えが合わないパラドックスの感覚が面白く、数学者でも間違えるくらいの問題として有名になりました。
この記事では、モンティ・ホール問題の紹介、条件付き確率やベイズの定理との関係性、感覚的に理解するためのポイントについて解説しています。
誰かに紹介したくなるような面白い問題なので、自分だったらどれを選ぶか、ご自身の直感と照らし合わせながら、いっしょに考えてみてください。
モンティ・ホール問題とは?
問題
モンティ・ホール問題とは、実際にアメリカのテレビ番組で行われた景品当てゲームの問題のことで、番組の司会者モンティ・ホール氏が名前の由来となっています。
実際に取り上げられた問題は次の通りです。
あなたの前に3つのドアがあります。1つのドアの先は景品(車)、残り2つのドアの先にはハズレ(ヤギ)が待っています。
この中から、まずあなたが1つのドアを選びます。
そして、あなたが選んだドアを開ける前に、司会者が残り2つのドアからハズレの方を選んで開けます。
さて、あなたは最初に選んだドアをそのまま開けますか? それとも、残り1つのドアを選び直しますか?
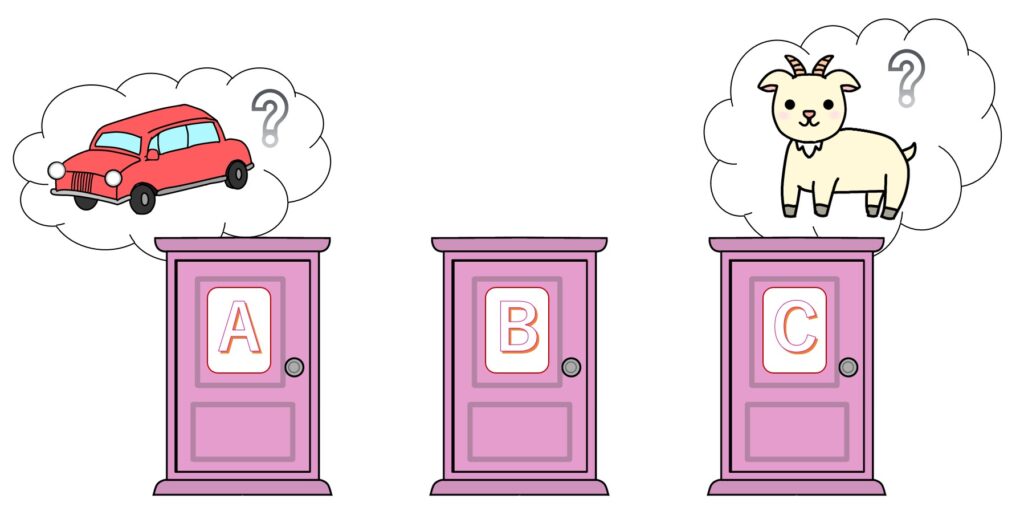
日常生活のどこにでもあるような問題で、問題の内容そのものも大変シンプルで分かりやすいものですね。
しかし、こんな単純な問題が数学者を巻き込んで、全米を震撼させるような話題になってしまうのです。
答え
さて、問題文を見て、どのような直感が働いたでしょうか?
ドアは残り2個・・片方が当たりで、もう片方がハズレだから、どちらも$\frac{1}{2}$で変えても変えなくても同じ!
・・と思った方も多いのではないでしょうか。
先に答えを言うと、実は、ドアを変えなかった場合に景品が当たる確率は$\frac{1}{3}$、ドアを変えた場合の確率は$\frac{2}{3}$となり、何と2倍もの違いがあるというのです。

あれっ、同じじゃないの?
私は、この事実を感覚的に理解して受け入れるのに、かなり時間がかかりました。
上にも述べたように、変えなくても同じじゃないかというイメージに支配されてしまい、どうしてもパラドックスの感覚から抜け出せなくなっていたのです。
解説
それでは、なぜ2倍の違いがある結果になるのか、解説していきます。
まず、最初にあなたがドアを選んだ時点、この状態ではランダムなので当たる確率は$\frac{1}{3}$です。
ここで、仮に、あなたが「A」のドアを選んだとしましょう。
すると、司会者は「B」「C」のいずれかを開けることになります。
もう少し具体的に考えるために、場合分けをしてみます。
①:Cが当たりの場合
あなたが最初に選んだドアAはハズレです。
そして、司会者は残ったB、Cのうちハズレの方を開けてくれるので、司会者はBのドアを開けることになります。
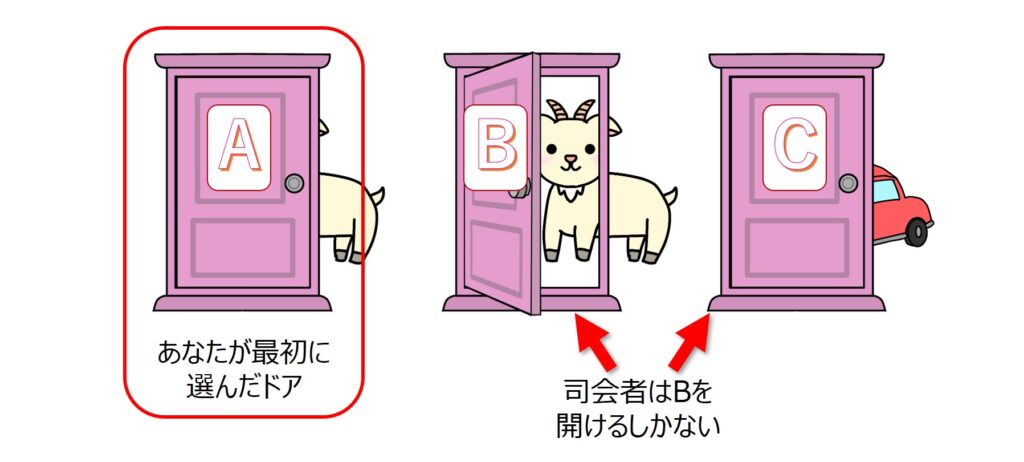
つまり、「ドアを選び直したら当たる」と言えます。
②:Bが当たりの場合
先ほどと同じように、「ドアを選び直したら当たる」と言えます。
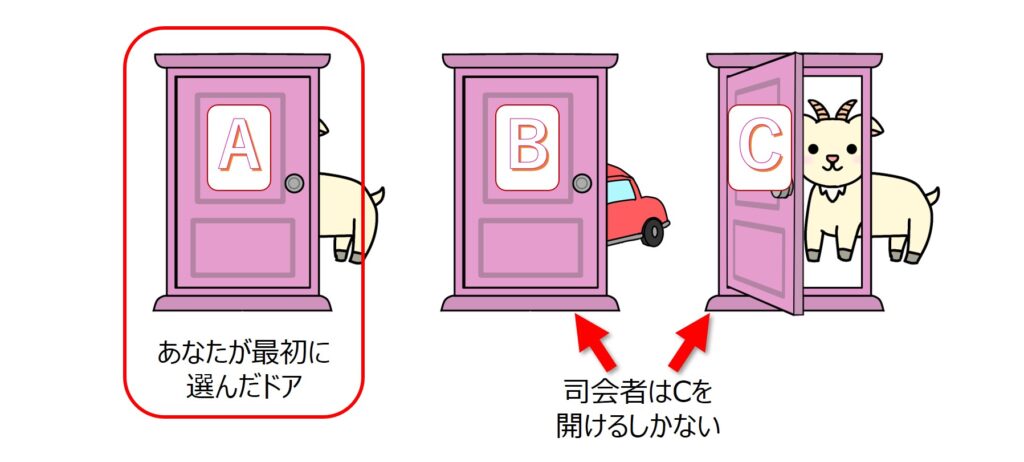
③:Aが当たりの場合
残りBとCのドアはどちらもハズレなので、司会者はどちらを開ける可能性もあります。
しかし、司会者がどちらを選んだにせよ、あなたがドアを選び直すとハズレが待っています。
つまり、「最初のドアから変えなければ当たる」と言えます。
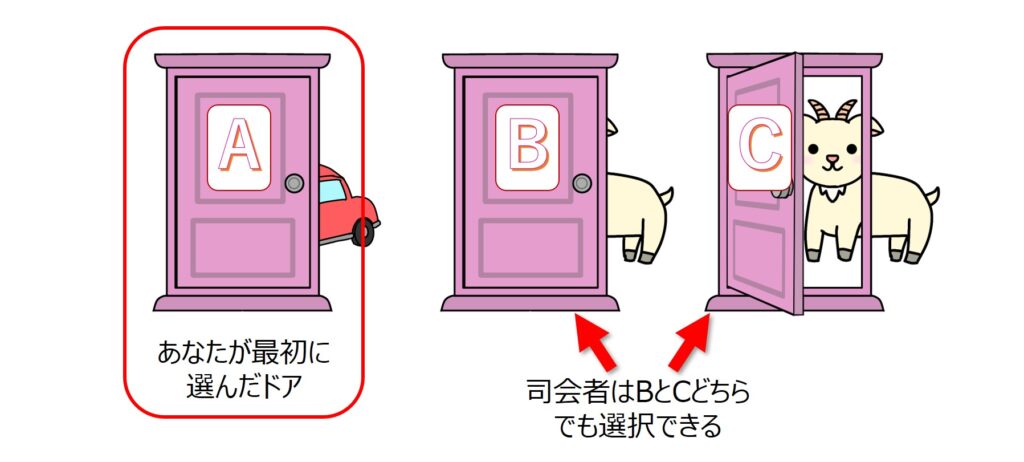
整理すると、次のようになります。
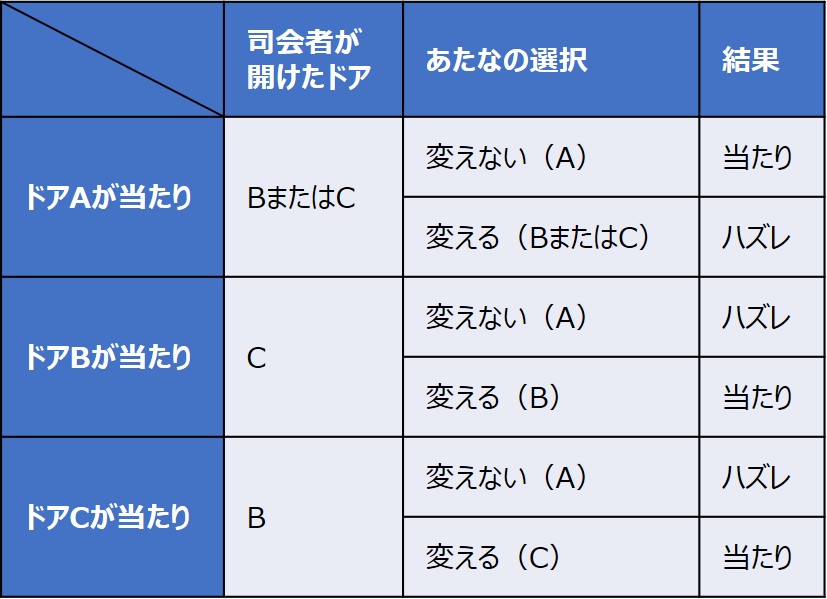
表を見て分かることは、「最初に当たりを選んだ場合、ドアを選び直すとハズレ」 「最初にハズレを選んだ場合、選び直すと当たり」という関係性です。
最初にハズレを選ぶ確率は$\frac{2}{3}$なので、選び直した方がお得という結論になるのです。

うっかり変えないところだったよ
確率の公式から求める
条件付き確率
条件付き確率とは、事象Aが起きたもとで、事象Bが起きる確率のことで、$P(B\mid{A})$または$P_{A}(B)$と記載されます。
詳しくは、こちらの記事で解説していますので、定義や公式をあらためて確認したい方はご覧ください。

モンティ・ホール問題を条件付き確率に当てはめて考えてみましょう。
まず、あなたが選ぶドアをAとして固定します。
そして、ドアAが当たる事象を大文字A(B、Cも同様)、司会者がドアAを開ける事象を小文字a(b、cも同様)と置くことにします。
すると、各パターンの確率をマトリックスに表すと以下のようになります。
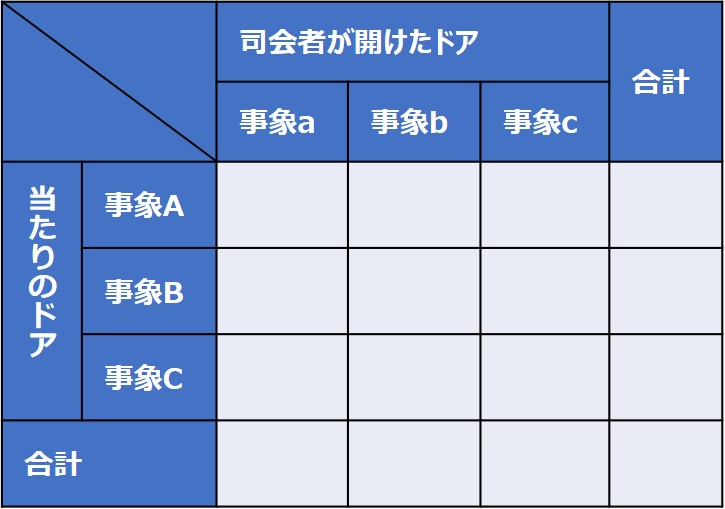
この表の確率を埋めていきましょう。
まず、事象A~Cの確率(それぞれのドアが当たる確率)は均等となるので、全て$\frac{1}{3}$となります。
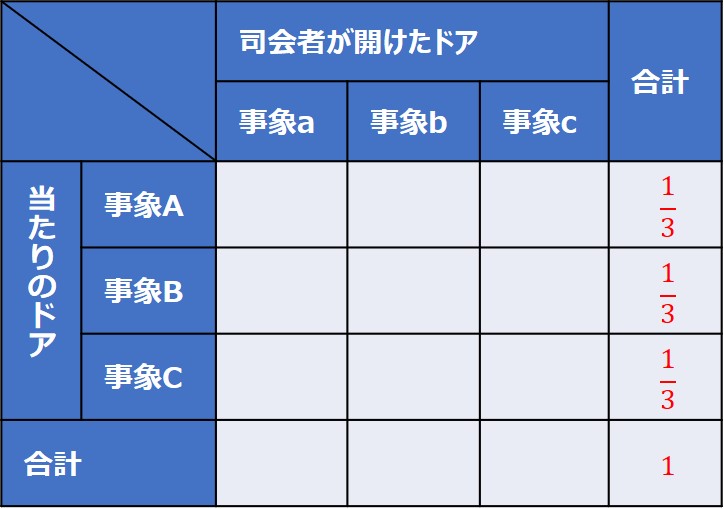
次に、事象a(司会者がドアAを開ける)の確率に着目すると、あなたがドアAを選んでいる段階で同時に起きることはないので、全てゼロになります。
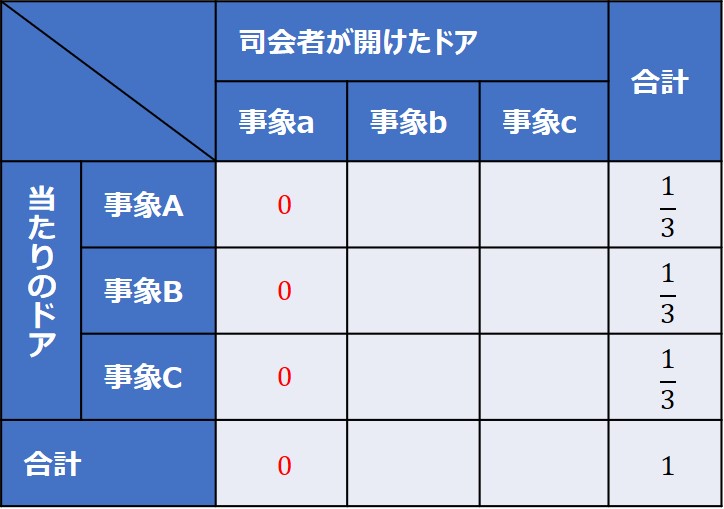
また、少し見方を変えて、事象Bまたは事象C(ドアBまたはCが当たり)の確率に着目すると、先ほども説明したように司会者が選ぶドアは一択となり、他はゼロとなります。
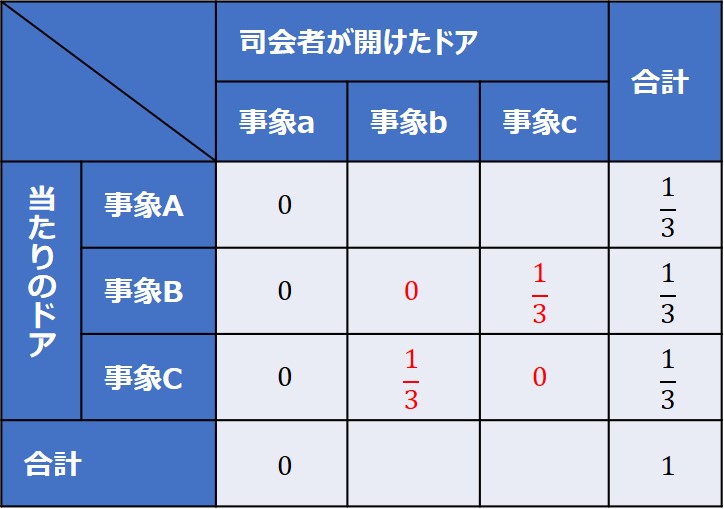
事象Aの場合は、司会者はBまたはCのドアを開けるので、事象bと事象cが均等な確率になります。
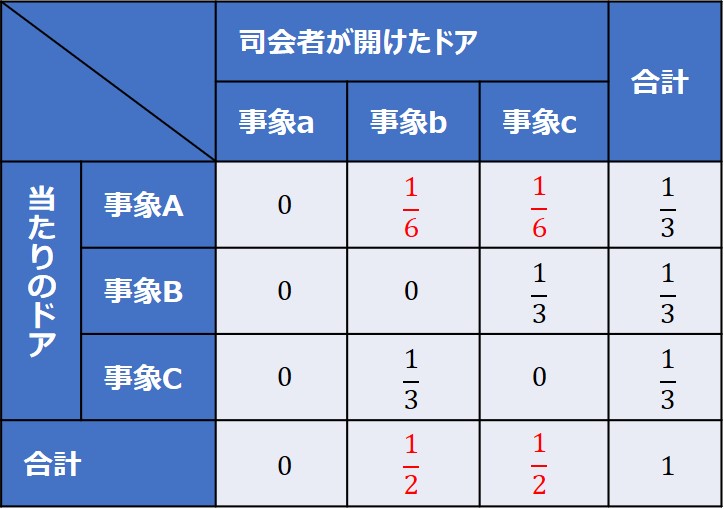
マトリックスをすべて埋めると、このようになりました。
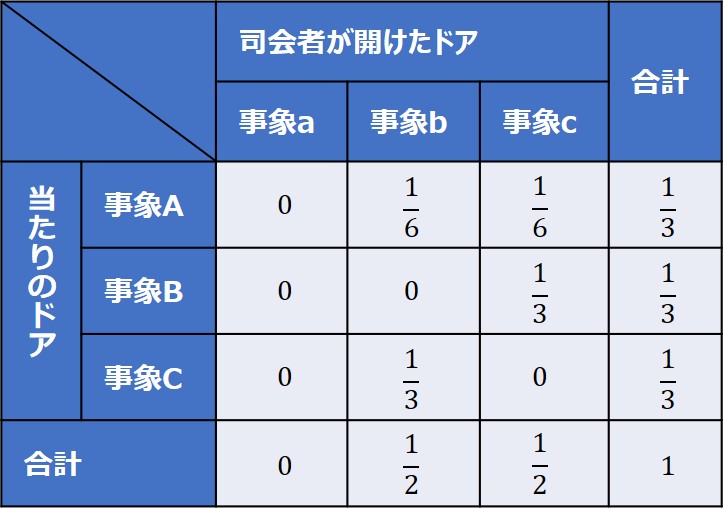
さて、あなたがドアAを選んでいる場合に、司会者が例えばBのドアを開けた(事象b)としましょう。
条件付き確率の公式によると、この時にドアAが当たる確率は$\frac{1}{6}$ ÷ $\frac{1}{2}$ = $\frac{1}{3}$、ドアCが当たる確率は $\frac{1}{3}$ ÷ $\frac{1}{2}$ = $\frac{2}{3}$となります。
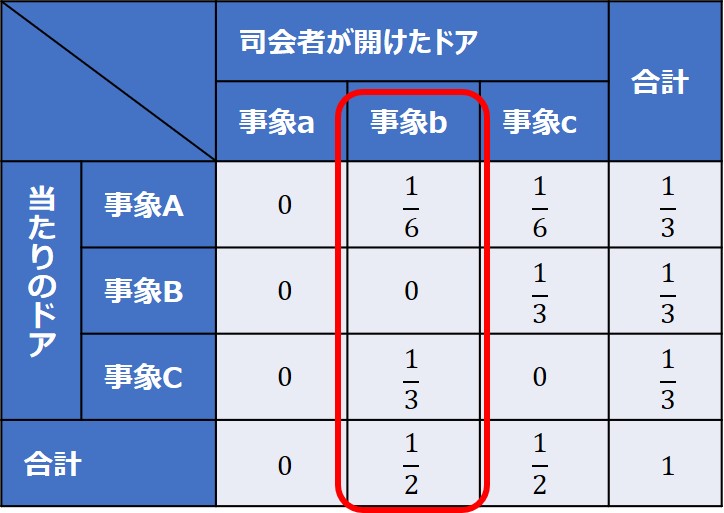
つまり、ドアを選び直した方が良いという結果が、計算からも求められることが分かりましたね。
ベイズの定理
ベイズの定理とは、因果関係の成り立つ条件付き確率において、$P(結果|原因)$, $P(原因)$, $P(結果)$の3つの確率から、$P(原因|結果)$を求めるために用いられる関係式のことです。

直接的に求めにくい確率に対し、因果関係を入れ替えて求めやすい確率から間接的に求めることに効果を発揮するもので、モンティ・ホール問題を考える上でも活用できます。
例えば、あなたがドアAを選んでいるとして、「司会者がドアBを開けた時に、ドアCに変更して当たる確率」を $P(C\mid{b})$と置くと、ベイズの定理により以下の関係式が成り立ちます。
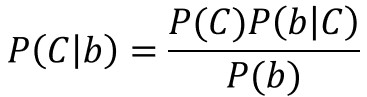
$P(b)$は司会者がドアBを開ける確率で$\frac{1}{2}$、$P(C)$はドアCが当たりの確率で$\frac{1}{3}$となります。
さらに、因果関係を入れ替えた$P(b\mid{C})$に着目すると、「ドアCが当たりの場合に司会者がドアBを開ける確率」と表現することができます。
ここで、$P(b\mid{C})$が1になることにお気づきでしょうか。
ドアCが当たりという条件付き確率では、司会者はもう片方のドアを開けるしかないので、確率は1になります。
つまり、$P(b\mid{C})$は以下のように求められます。
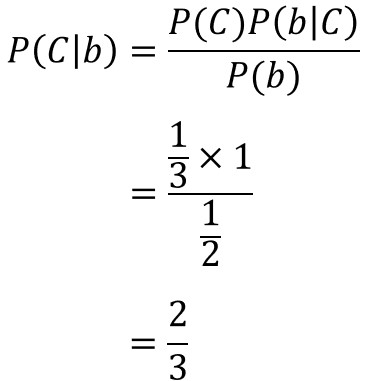
ベイズの定理からも、同じ結果が得られることが分かりましたね。

数式で考えると感覚に惑わされないね
感覚的に理解しやすくなるポイント
1.ドアに名称を付けて識別する
3つのドアをごちゃ混ぜに考えると、頭の中の整理が追い付かず、混乱して正しい確率の計算ができなくなってしまいます。
司会者が選ぶドアが残った方のどちらなのか、きちんと3つを識別できるよう、今回のようにA~Cなど名称を割り振って考えると混乱が生じにくいです。
2.場合分けを書き出してみる
あなたがドアを選ぶという行為と、司会者がドアを開けるという行為を同時に考える必要があるため、場合分けのケースが多く複雑になってしまいます。
「○○の場合」といった表現で列挙するか、条件付き確率のように表にするなど、パターンを書き出して視覚化すると、とても分かりやすくなります。
3.ドアの数を増やして考える
直感的な感覚のずれが邪魔して、どうしても固定観念から脱却できないという方には、いったんドアの数を増やした場合を想定して考えてみることも試してみてはいかがでしょうか。
例えば、ドアの数が100個の場合を想定してみてください。
あなたが、とあるドアを選んだとして、続いて、司会者が当たりではない残り98個のドアを開けたとします。
さて、残った2つのドアに対し、選択を変えた方が良いのかどうか、どう思いますか?
何となく、自分が最初に選んだドアよりも、司会者が残したドアの方が当たりそうな予感がしませんか。
自分が選んだドアは100個のうちの1個に過ぎませんが、司会者が残したドアは当たりを避けて残り続けたドアであり、当然、当たりである確率が高いものになっています。
つまり、司会者がドアを開けるという行為は、残ったドアからハズレを除外してくれるという条件付き確率を表しており、数が多ければ多いほどその効果が直感的にも見えてくるのです。
ここまで紹介した3つの考え方を用いれば、真の確率を見抜くにあたって、パラドックスの感覚を少しでも払拭できたのではないでしょうか。
まとめ
- モンティ・ホール問題
⇒実際にアメリカのテレビ番組で行われた景品当てゲームの問題のことで、番組の司会者モンティ・ホール氏が名前の由来となった確率の問題 - 解き方
⇒場合分けや条件付き確率、ベイズの定理を用いることで確率の問題として解くことができる - 感覚的に理解しやすくなるポイント
⇒ドアに名称を付けて識別する
場合分けを書き出してみる
ドアの数を増やして考える
直感では理解にしにくかった問題でも、条件付き確率やベイズの定理など理屈に従って順を追って考えていけば、何となくお分かりいただけたでしょうか。
今回のような日常的な題材でのパラドックスとして、少しでも確率の世界を身近に感じてもらえたらうれしいです。





コメント