「定理の公式と証明を知りたい」
「公式の意味とメリットは何?」
「役に立つ例題を知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
ベイズの定理とは、因果関係の成り立つ条件付き確率において、$P(結果|原因)$, $P(原因)$, $P(結果)$の3つの確率から、$P(原因|結果)$を求めるために用いられる関係式のことです。
いきなり、$P(結果|原因)$や$P(原因|結果)$と言われてもピンと来ないと思いますが、心配する必要はありません。
この記事では、初心者の方にもわかりやすいよう、ベイズの定理の成り立ちと証明、活用するメリットについて、仕事や日常生活で使える例題を交えながら解説しています。
とてもシンプルな公式で覚えやすいので、ぜひ最後まで読んで参考にしていただければと思います。
ベイズの定理とは?
公式
まず初めに、ベイズの定理では条件付き確率の考え方や公式を用いることを前提としていますので、条件付き確率の予備知識に不安のある方は、こちらの記事からご覧ください。

ベイズの定理とは、因果関係の成り立つ条件付き確率において、$P(結果|原因)$, $P(原因)$, $P(結果)$の3つから、$P(原因|結果)$を求めるために用いられる以下の関係式のことを表します。
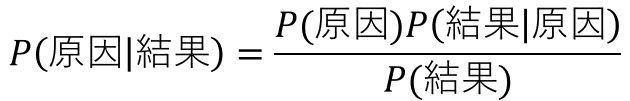
結果にあたる事象を事象$A$、原因を事象$B$と置き換えて、以下の関係式で表現することもあります。
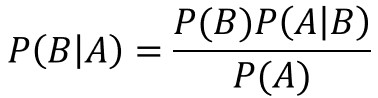
関係式の成り立ちはとてもシンプルで覚えやすいですね。

AとBの順序が重要だから間違えないようにしよう
証明
ベイズの定理は、条件付き確率の公式から導き出すことができます。

この公式では、事象$B$にあたるものが1つの場合を想定したものですが、$k$種類の事象として拡張して表現すると以下のようになります。
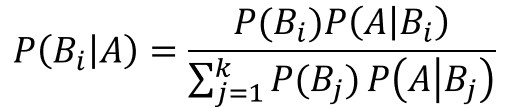
ベイズの定理の意味とメリット
さて、ベイズの定理の公式がわかったところで、いったいどういう意味があるのか、何の役に立つのか、漠然としているのではないでしょうか。
ここでは、よくある例題として迷惑メールの振り分け機能を題材として、公式の意味を解説していきます。
過去の調査結果から、全てのメールのうち10%が迷惑メールであることが分かっています。また、迷惑メールの中で「広告」という単語の含まれる確率が30%、一般メールの中では5%であることが分かっています。無作為に選んだメールに「広告」という単語が含まれていた場合、このメールが迷惑メールである確率はいくつでしょうか?
実際に計算して答えを求めるのは、後の例題であらためて解説しますので、ここでは、公式の意味と用語の使い方、ベイズの定理を使うメリットにフォーカスして説明します。
項目の分類
ベイズの定理に当てはめるため、まずは項目を分類します。
今回の例題では、“迷惑メール”、“一般メール”、“「広告」という単語を含む”、“「広告」という単語を含まない”、という4つのキーワードに分かれます。
そして、事象$A$、事象$B$に割り付けます。
事象$A$:「広告」の単語を含む
事象$A$の余事象:「広告」の単語を含まない
事象$B_{1}$:迷惑メール
事象$B_{2}$($B_{1}$の余事象):迷惑メールでない(一般メール)
求めたい確率は、「広告」という単語を含むメールにおける、迷惑メールである確率です。
つまり、事象$A$の条件下での事象$B_{1}$が起こる確率、条件付き確率$P(B_{1}|A)$に該当します。
さらに、問題文から分かっている確率を当てはめると以下のようになります。
$P(B_{1})$:0.1(迷惑メールである確率)
$P(B_{2})$:0.9(一般メールである確率)
$P(A|B_{1})$:0.3(迷惑メールという条件下で「広告」を含む確率)
$P(A|B_{2})$:0.05(迷惑メールでない条件下で「広告」を含む確率)
関係性を図示すると以下のようになります。
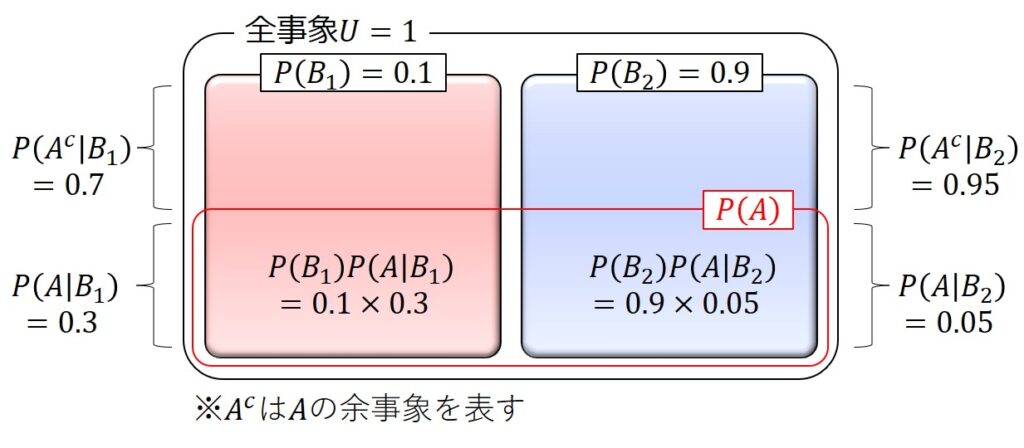

記号や数式よりも図で覚えた方が分かりやすいね
公式の意味とメリット
ここで、もう一度、ベイズの定理の公式を振り返ってみましょう。
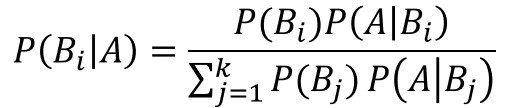
$i=1$, $k=2$と置くと次のようになります。
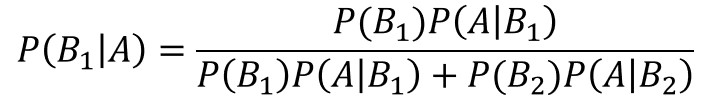
$P(B_{1}|A)$を求めるために必要な情報がすでに揃っていることに気づいたでしょうか。
ベイズの定理のメリットは、$P(B_{1})$, $P(B_{2})$, $P(A|B_{1})$, $P(A|B_{2})$が分かっていれば、$P(B_{1}|A)$を算出できることにあります。
数式だけでは分かりにくいかもしれませんが、感覚的な表現をすると、$P(B_{1})$, $P(B_{2})$, $P(A|B_{1})$, $P(A|B_{2})$は求めやすい確率、$P(B_{1}|A)$は求めにくい確率に近いイメージとなります。
時系列で言うと、まず、迷惑メールに振り分けられるかどうかが最初に起こる事象で、そこに「広告」という単語が含まれているかどうかが結果として分かります。
つまり、迷惑メールか否か⇒「広告」が含まれるか否かの順で分類されることから、原因と結果の対応の関係にあたるのです。
そして、「結果から原因を求める」ことよりも、「原因から結果を求める」方がはるかに簡単なことが多いのです。
例えば、$P(A|B_{1})$(迷惑メールという条件で「広告」を含む確率)は、過去の調査結果などをもとにした既知の情報で、今回の事例でも問題文に与えられる前提条件となっています。
これに対して、「広告」を含むメールが迷惑メールであったかどうかは、前提条件として不明であることが多く、直接的に出すことができません。
ベイズの定理では、このような直接的に求めにくい確率に対し、因果関係を入れ替えて求めやすい確率から間接的に求めることに効果を発揮するのです。
よく使う用語
ベイズの定理の意味が分かったところで、用語を紹介しておきます。
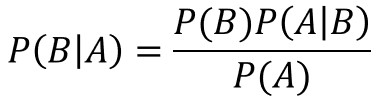
事前確率:原因となる事象が起こる前の確率 $P(B)$
事後確率(逆確率):原因となる事象が起こった後の確率 $P(B|A)$
尤度(ゆうど):$P(A|B)$
尤度というのは、尤も(もっとも)らしいという言葉を由来にしており、原因に対する結果の確率が分かるのは尤もらしいことという意味です。
例題
例題1:迷惑メールの自動振り分け
過去の調査結果から、全てのメールのうち10%が迷惑メールであることが分かっています。また、迷惑メールの中で「広告」という単語の含まれる確率が30%、一般メールの中では5%であることが分かっています。無作為に選んだメールに「広告」という単語が含まれていた場合、このメールが迷惑メールである確率はいくつでしょうか?
解説
事象$A$:「広告」の単語を含む
事象$A$の余事象:「広告」の単語を含まない
事象$B_{1}$:迷惑メール
事象$B_{2}$($B_{1}$の余事象):迷惑メールでない(一般メール)
$P(B_{1})$:0.1(迷惑メールである確率)
$P(B_{2})$:0.9(一般メールである確率)
$P(A|B_{1})$:0.3(迷惑メールという条件下で「広告」を含む確率)
$P(A|B_{2})$:0.05(迷惑メールでない条件下で「広告」を含む確率)
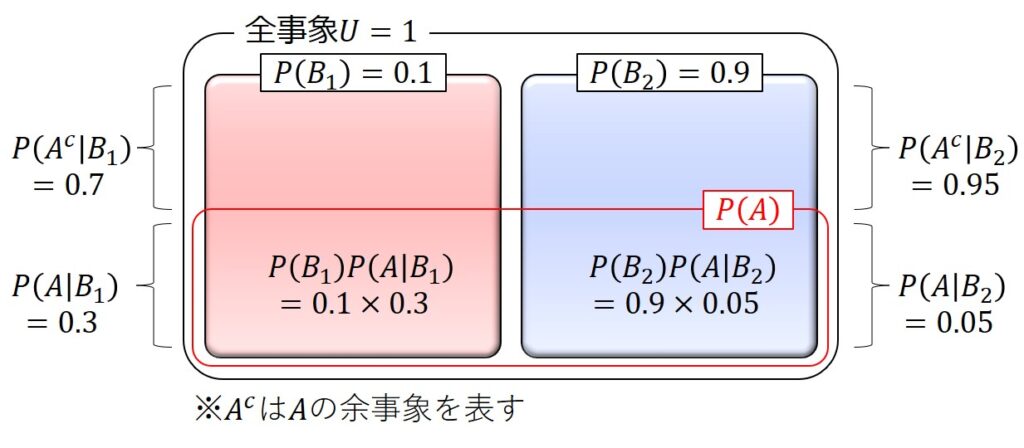
ベイズの定理の公式に当てはめると、以下の通り求められます。

答えは、$40$%となります。
例題2:陽性になる確率は?
1万人に1人の割合で罹患する病気があったとします。この病気の陽性/陰性を判定する検査において、誤判定する割合が1%であったとします。Aさんが陽性と判定されたとき、本当に病気にかかっている確率はいくつでしょうか?
解説
事象$A$:陽性判定となる
事象$A$の余事象:陰性判定となる
事象$B_{1}$:病気に罹患している
事象$B_{2}$($B_{1}$の余事象):病気に罹患していない
$P(B_{2})$:0.9999(病気に罹患していない確率)
$P(A|B_{1})$:0.99(病気に罹患した場合に陽性判定となる確率)
$P(A|B_{2})$:0.01(病気に罹患していない場合に陽性判定となる確率)
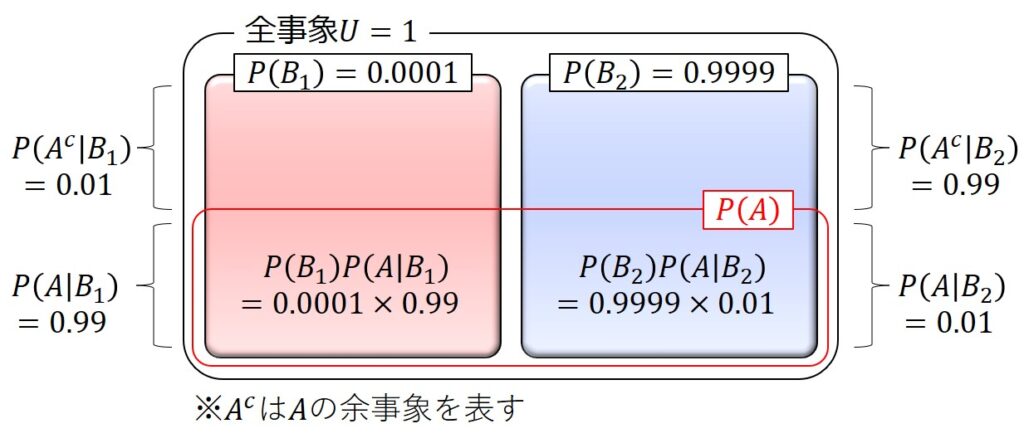
ベイズの定理の公式に当てはめると、以下の通り求められます。

陽性と判定されたのに、実際に病気である確率が0.98%というのは感覚と合わない気がしますが、そもそも病気になる確率が低いことを考えると、真実はこの程度ということです。

例題3:不良品が作られた製造工場は?
とある製品は、工場A、工場B、工場Cの3つの工場で作られています。生産数量の比率は、それぞれ50%、30%、20%です。また、それぞれの工場における不良の発生率は、1%、2%、5%という調査結果が得られています。ここで、とある不良品がどの工場で製造されたのか不明な場合において、工場Cで生産されたものである確率はいくつでしょうか?
解説
事象$A$:不良品が発生する
事象$B_{1}$:工場Aで生産された
事象$B_{2}$:工場Bで生産された
事象$B_{3}$:工場Cで生産された
$P(B_{1})$:0.5(工場Aで生産された確率)
$P(B_{2})$:0.3(工場Bで生産された確率)
$P(B_{3})$:0.2(工場Cで生産された確率)
$P(A|B_{1})$:0.01(工場Aで生産された場合に不良品が発生する確率)
$P(A|B_{2})$:0.02(工場Bで生産された場合に不良品が発生する確率)
$P(A|B_{3})$:0.05(工場Cで生産された場合に不良品が発生する確率)
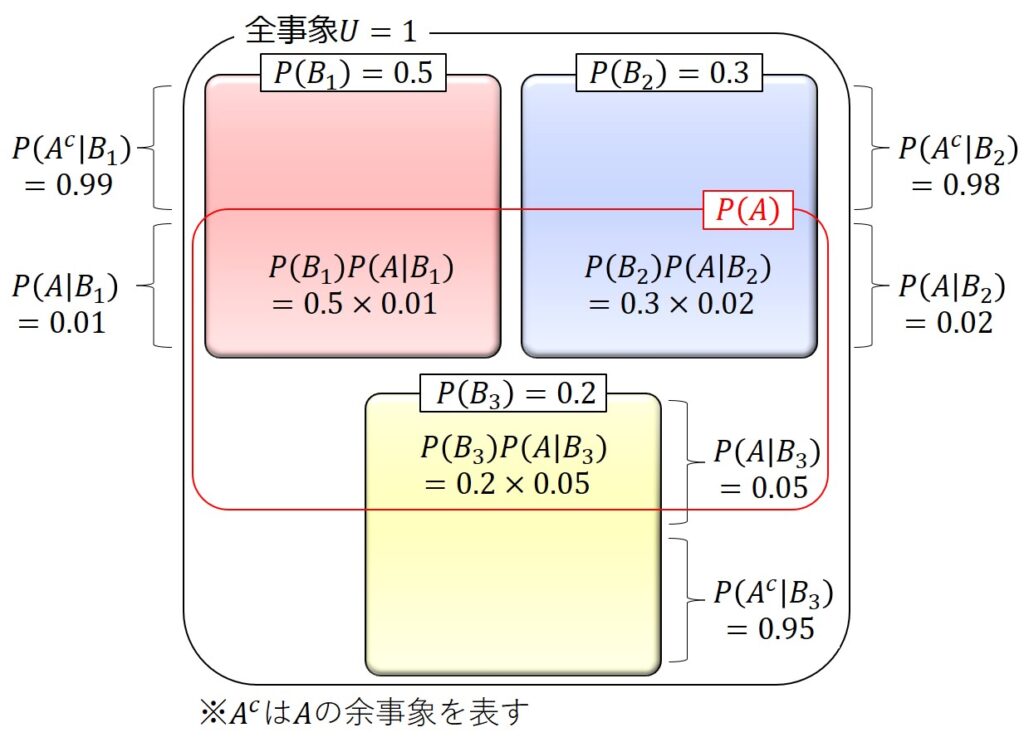
ベイズの定理の公式に当てはめると、以下の通り求められます。
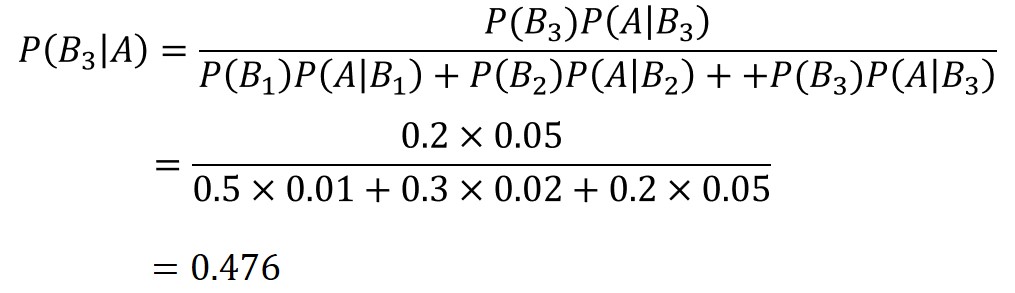
答えは、$47.6$%となります。
工場Cの品質が他と比べて劣ることが分かりますね。

確率で数字にして分析すると分かりやすいなぁ
まとめ
- ベイズの定理
⇒因果関係の成り立つ条件付き確率において、$P(結果|原因)$, $P(原因)$, $P(結果)$の3つの確率から、$P(原因|結果)$を求めるために用いられる関係式 - メリット
⇒直接的に求めにくい確率に対し、因果関係を入れ替えて求めやすい確率から間接的に求めることができる - 用語
⇒事前確率:原因となる事象が起こる前の確率 $P(B)$
事後確率(逆確率):原因となる事象が起こった後の確率 $P(B|A)$
尤度(ゆうど):$P(A|B)$
仕事や日常生活の例題を見て、身近に感じた方も多かったのではないでしょうか。
直感を信じて解こうとすると、感覚と合わない場合もあるので、計算の確実性を上げるためにも、ベイズの定理を覚えておくと大変便利です。
製造ラインの不良率の問題など、実務に応用できる題材も多いので、ぜひ一度試してみてください。





コメント