「そもそも二次元分布って何?」
「二次元正規分布の定義を知りたい」
「数式が複雑でイメージが掴めない」
このような疑問や悩みをお持ちの方に向けた記事です。
二次元正規分布とは、2つの確率変数を持つ正規分布のことです。
日常生活や普段の業務で取り扱う現象は、必ずしも確率変数が1つの一次元であるとは限りません。
しかし、一次元が二次元に拡張されるだけで、数式も格段に複雑になり、確率分布も視覚的に捉えることが難しくなります。
この記事では、二次元分布の種類と性質、中でも最も代表的な二次元正規分布の確率密度関数の定義について解説しています。
また、二次元正規分布の形状を視覚的に掴めるよう、エクセルを用いたグラフの作成方法、相関係数の違いによる分布の形状への影響についても紹介します。
「多変量」という表現に苦手意識を持つ方にとって、イメージを掴む参考になればうれしいです。
二次元分布とは?
離散型同時確率分布
2つの確率変数$X$,$Y$を与えたときに、その発生確率を分布で表したものを同時確率分布と言います。
特に、確率変数が離散型の場合、離散型同時確率分布と呼ばれます。
離散型確率分布とは、確率変数が不連続な値を取る分布のことで、例えばサイコロの目や人数、個数といった計数値が変数となります。
数式では以下のように表現されます。
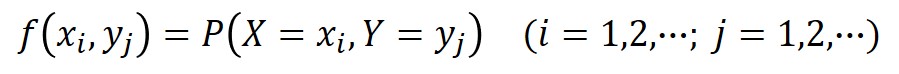
離散型同時確率分布の場合、$f(x,y)$は同時確率質量関数と呼ばれます。
また、二次元分布においても確率の総和は1となるので、以下の性質が成り立ちます。
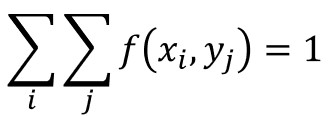
二次元分布の前に用語の定義をあらためて確認したい方は、合わせてご覧ください。


周辺確率分布
同時確率分布において、確率変数のひとつを固定し、もう一つの変数における確率の総和を表したものを周辺確率分布といいます。
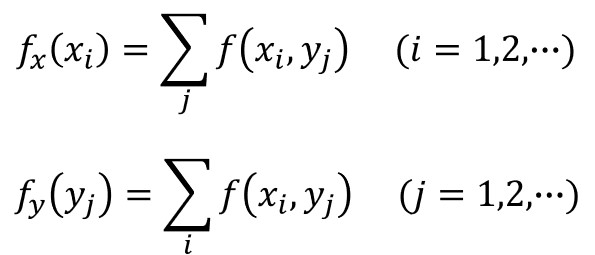
例えば、サイコロの目を例に挙げて見てみましょう。
赤いサイコロと青いサイコロの2つがあるとします。
出る目の確率が均等とすると、それぞれの確率変数と確率質量関数、周辺確率分布は以下のようになります。
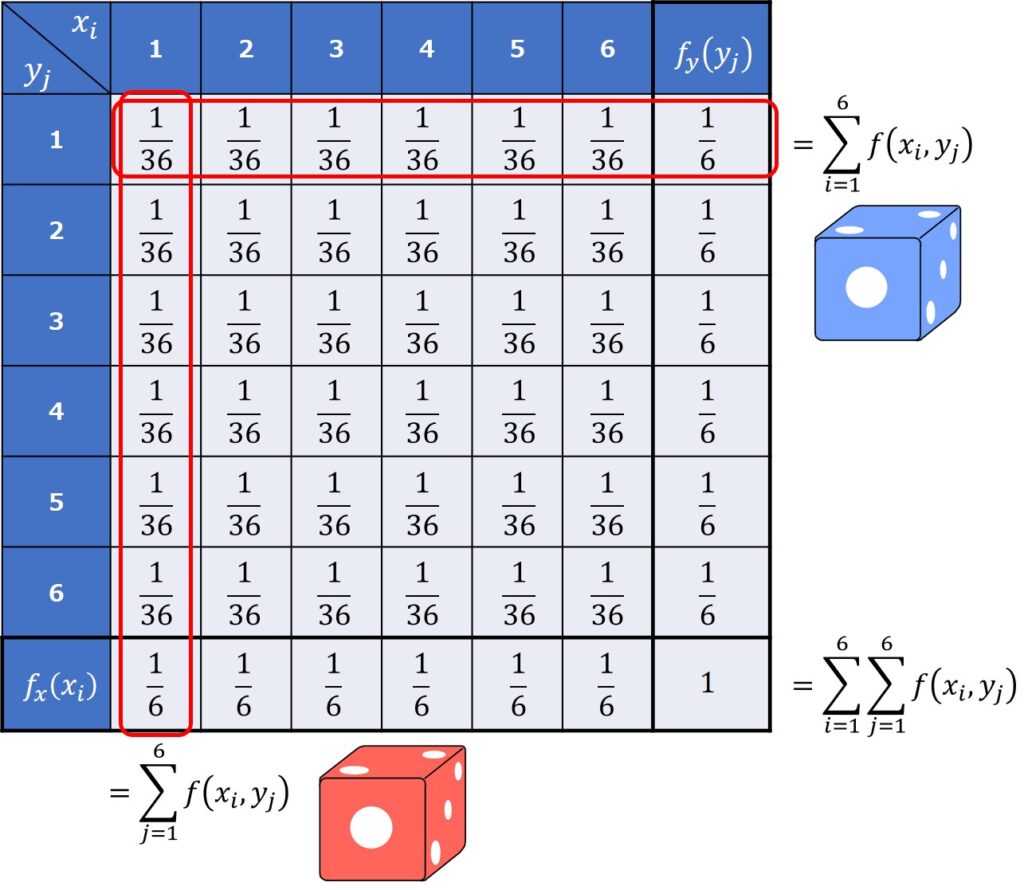

表にしたら分かりやすくなったね
連続型同時確率分布
確率変数が連続型の場合、連続型同時確率分布といいます。
連続型とは、確率変数が連続的な値を取る分布のことで、長さや質量といった計量値が変数となります。
数式では以下のように表現されます。
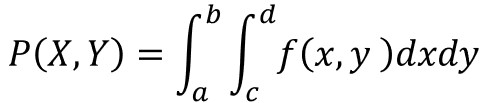
連続型同時確率分布の場合、$f(x,y)$は同時確率密度関数と呼ばれます。
確率の総和、周辺確率分布についても離散型と同様で、以下の数式で表されます。
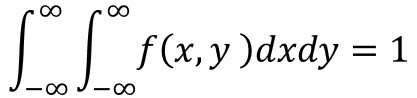
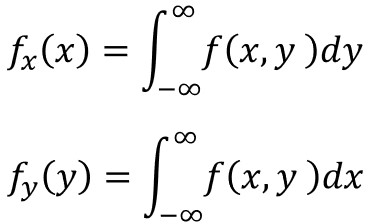
期待値と分散の公式
期待値
2つの確率変数を扱う場合の期待値は、以下の数式で求めることができます。
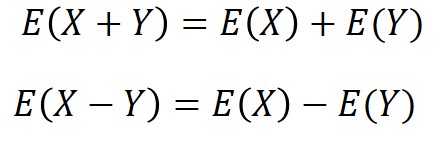
和(差)の期待値は、期待値の和(差)に等しくなる性質で、$X$,$Y$それぞれの期待値が分かれば簡単に計算できます。
これは、2つの確率変数が独立でない場合においても成り立つ関係です。
共分散
共分散とは、2変数の関係の強さを表す指標で$Cov(X,Y)$と表記され、以下の式で定義されます。
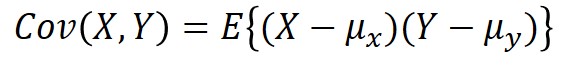
少し変形すると、以下の等式が成り立ちます。
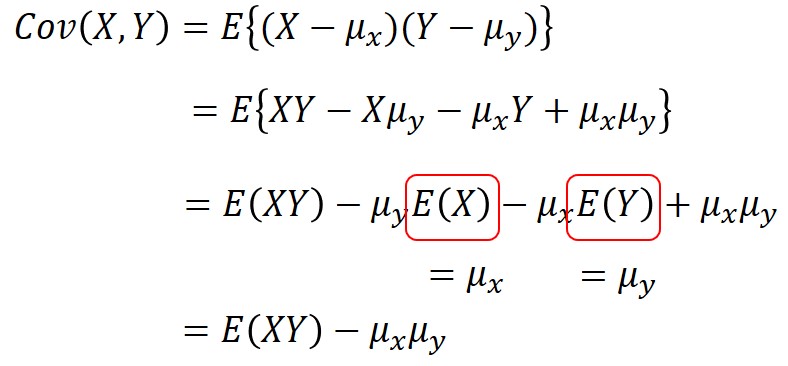
$X$,$Y$が互いに独立な場合(相関関係が無い場合)には、共分散はゼロとなります。
以下の記事で詳しく解説していますので、合わせて参考にしていただければと思います。

分散
分散は以下の数式で求められます。
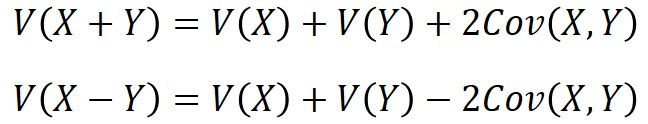
分散の場合、期待値のように分散の差になるわけではありません。
分散はデータのばらつきを示すもので、変数が増えた場合に、ばらつきが大きくなることは感覚的にも理解していただけるかと思います。
$X$,$Y$が互いに独立な場合は、共分散はゼロとなり、和の分散、差の分散ともに$V(X)+V(Y)$とシンプルな数式になります。

計算が楽ちんになるから公式は覚えておこう
二次元正規分布とは?
さて、ここからは二次元分布の具体例として、最も代表的な分布である二次元正規分布について見ていきましょう。
まず二次元の話に入る前に、一次元での正規分布について定義をあらためて確認したい方は、以下の記事をご覧ください。

確率変数が1つの場合における、確率密度関数は以下の式で定義されます。
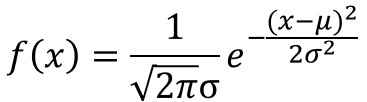
$e$はネイピア数(自然対数の底)、$μ$は平均値、$σ$は標準偏差を表します。
これを二次元に拡張すると、確率密度関数は以下のようになります。
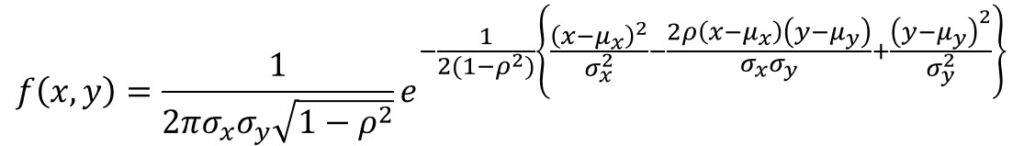
$ρ$は$X$と$Y$の相関係数を表します。
相関係数とは、共分散を標準化して単位を無次元化した指標のことで、共分散と標準偏差から以下の数式で求めることができます。
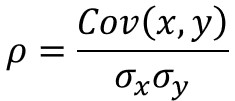
さて、変数がひとつ増えるだけで、各段に複雑な式になりましたね。
この数式が一体どのような分布を示すのか、相関係数の大小で分布の形状にどのような違いが表れるのか、エクセルを使って実際にグラフを書いて見ていきましょう。
エクセルでのグラフの書き方
独立した2変数の場合
確率変数$X$,$Y$が独立な場合、相関係数$ρ$がゼロとなるので、確率密度関数は以下のように変換できます。
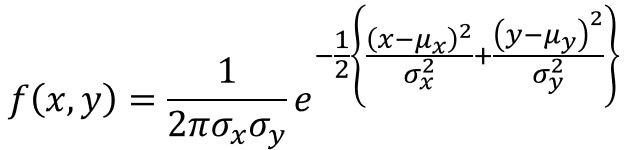
元の式と比べるとかなりスッキリしましたね。
さらに変換すると、以下のようになります。
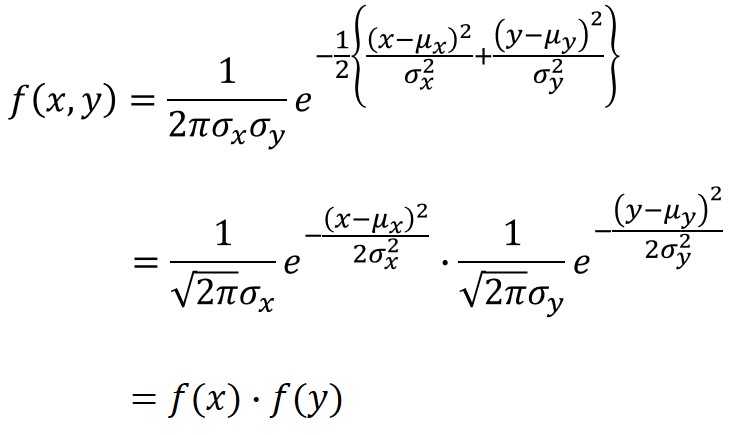
最終的に二次元の確率密度関数が、一次元の確率密度関数の積として表現されました。
一次元の正規分布の確率密度関数は、エクセルではNORM.DIST関数で求めることができます。
つまり、$X$に関するNORM.DIST関数と、$Y$に関するNORM.DIST関数を掛け合わせれば良いのです。
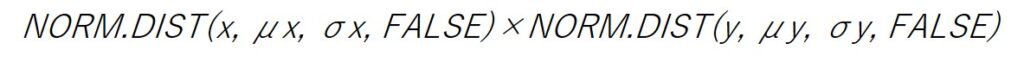
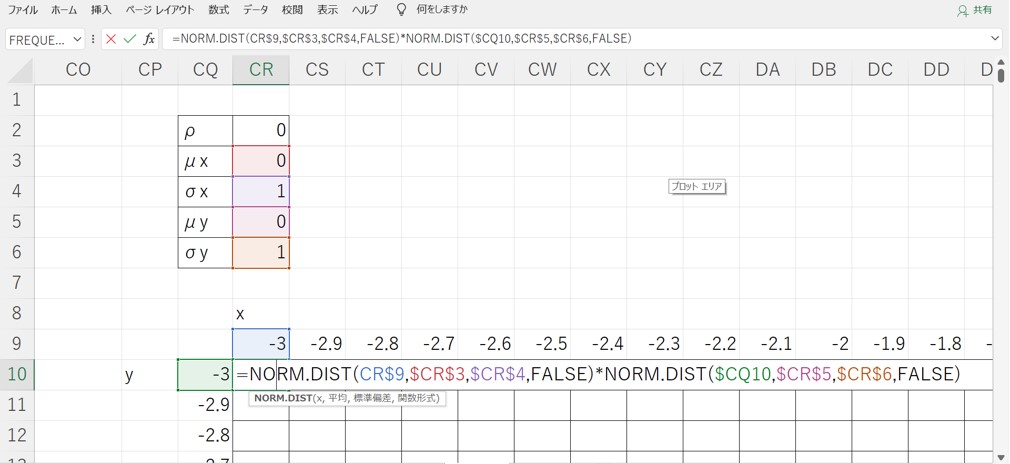
横軸に確率変数$X$、縦軸に確率変数$Y$を取り、マトリックスの交差する箇所に確率密度関数の値を入れます。
なお、等高線グラフでマトリックスの表全体を選択するだけで、2Dや3Dのグラフを簡単に作ることができます。
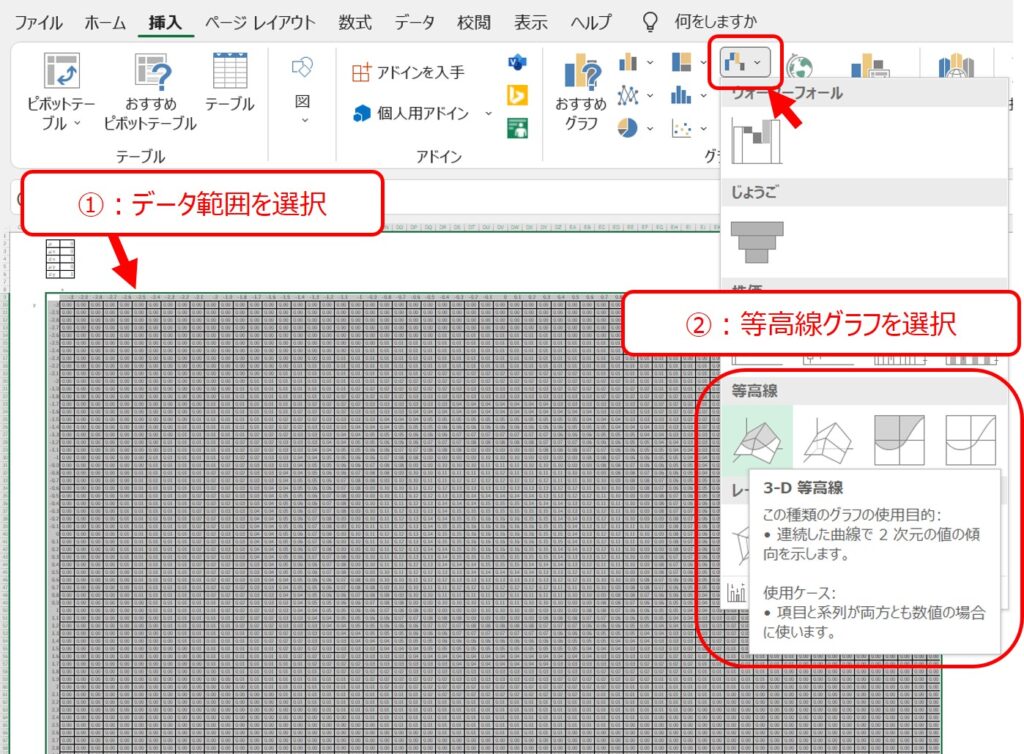
例えば、$μ_{x}=0, σ_{x}=1, μ_{y}=0, σ_{y}=1, ρ=0$と置いて、二次元標準正規分布の3Dグラフを書いてみると、以下のようになります。
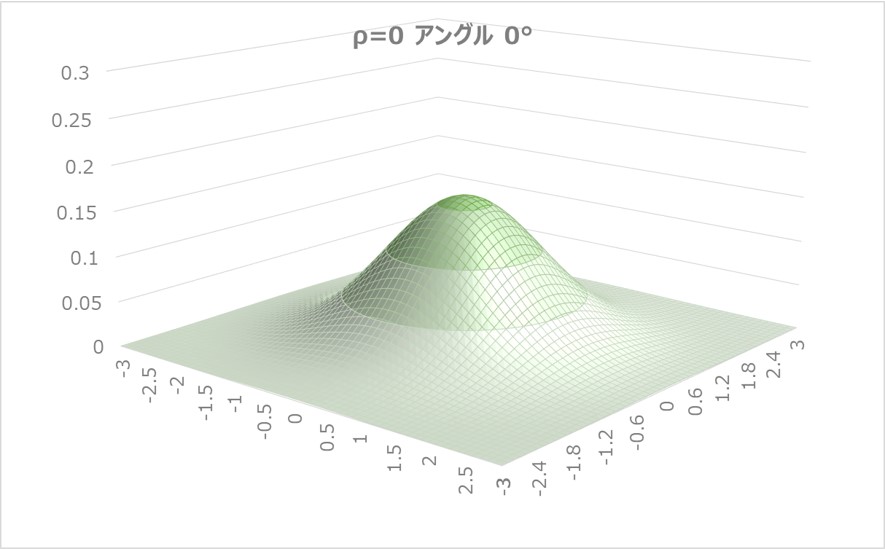
$X$,$Y$平面に対し、均等に分布していることが見て取れますね。
なお、このグラフは原点を中心とした等方向に広がる特殊な例ですが、通常の二次元正規分布では$(μx,μy)$を中心とした楕円になります。
相関のある2変数の場合
確率変数$X$,$Y$が独立でない場合は、NORM.DIST関数ひとつでは計算できず、以下の複雑な式をそのまま入力するしかありません。
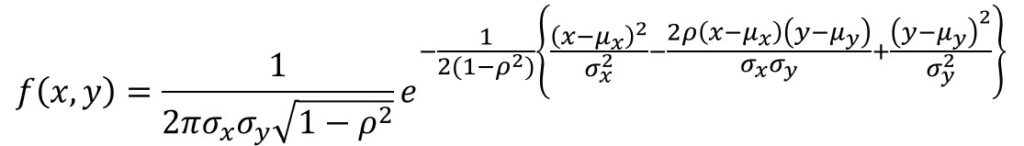
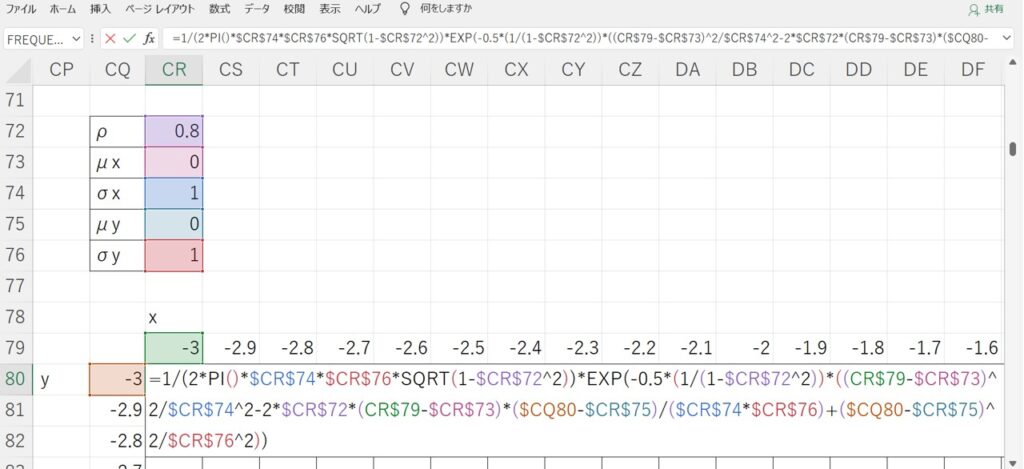
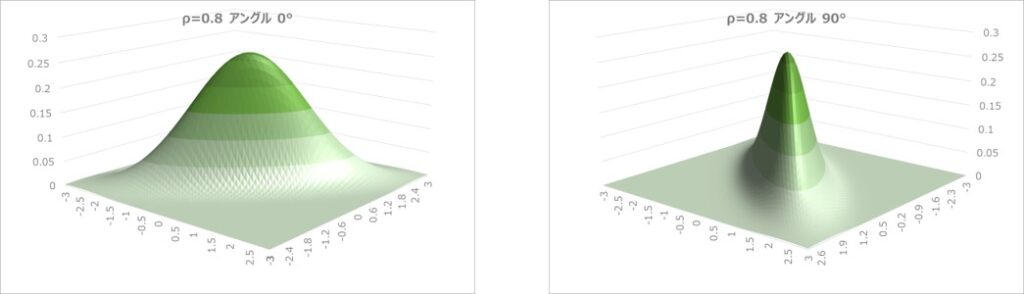
例えば、 $μ_{x}=0, σ_{x}=1, μ_{y}=0, σ_{y}=1, ρ=0.8$と置いて、二次元正規分布のグラフを書くと以下のようになります。
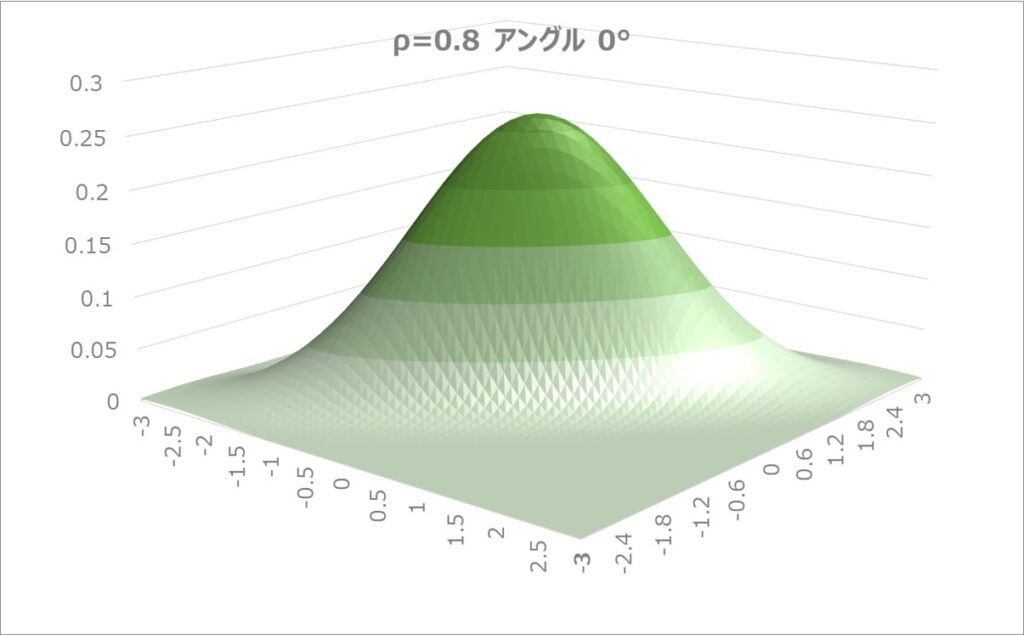
$X$,$Y$の相関の影響で平面方向に少しゆがんだ形状になることが見て取れます。
グラフのアングルを変えて90°回転してみると、このように平面方向に傾斜を持つことが良く分かります。
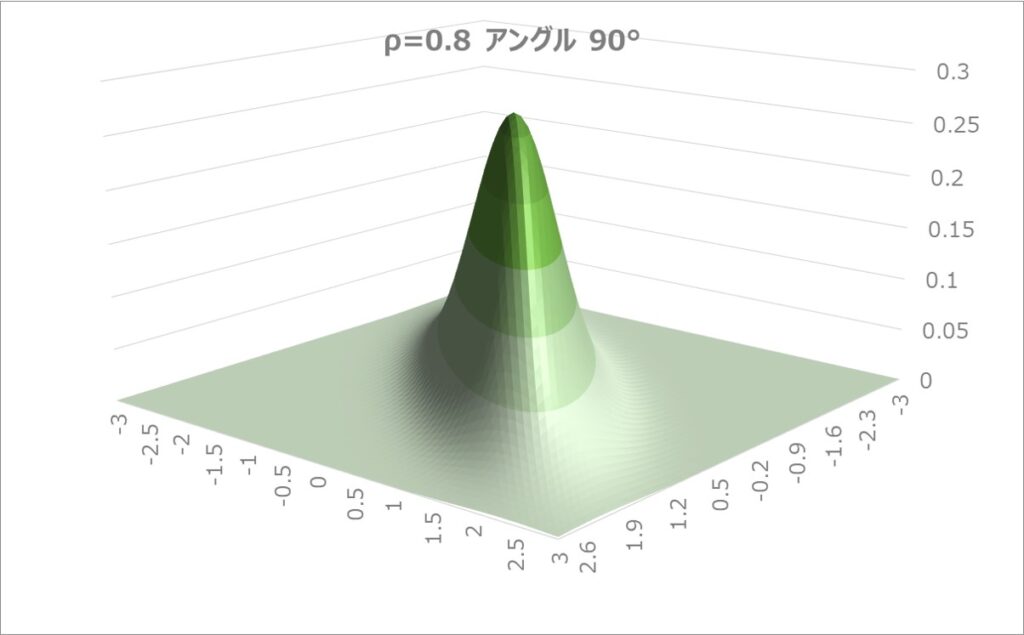

相関のある方向に集中しているってことだね
相関係数の違いによる影響
では、相関係数の違いにより、分布の形状にどのような変化が表れるのか見てみましょう。
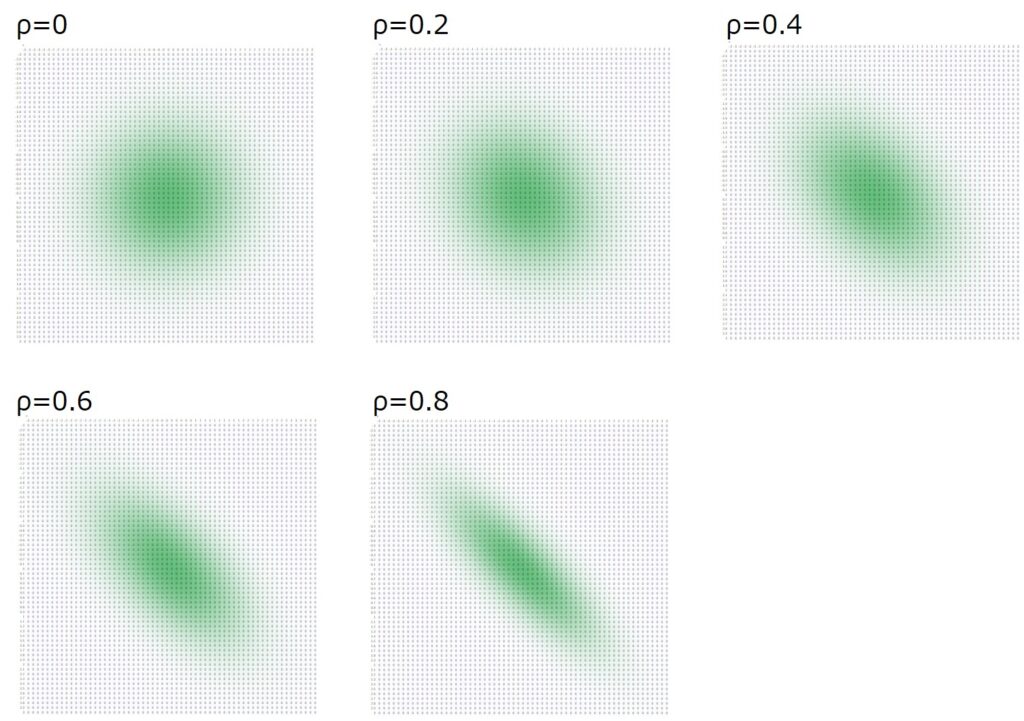
以下は、相関係数$ρ$を0~0.8まで変えたときの、二次元正規分布のグラフです。
相関係数が大きくなるほど、中央のピークが高くなり、面方向には均等性が崩れて薄っぺらい形状の分布になることが分かります。
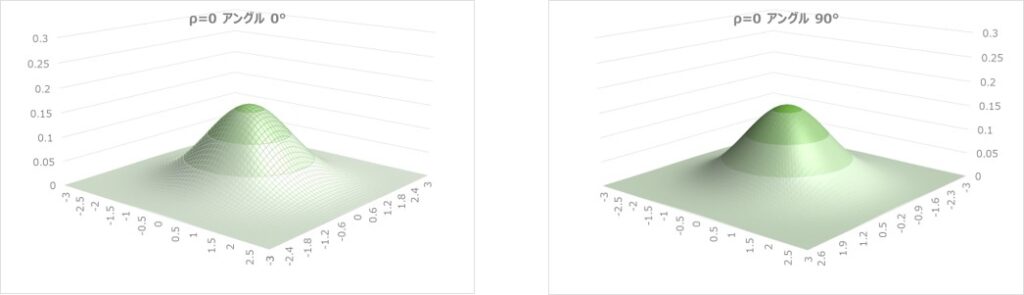
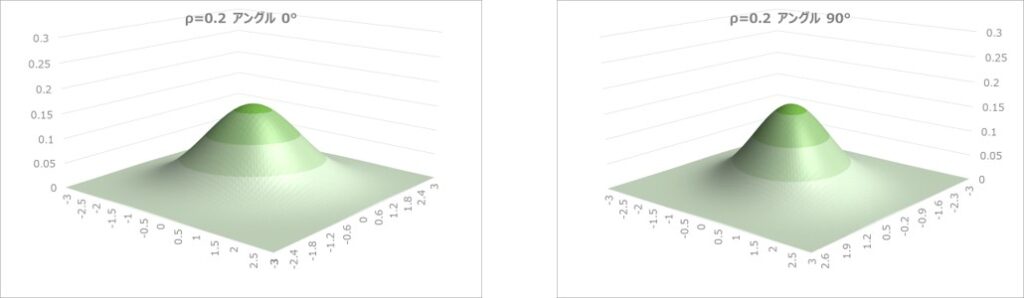
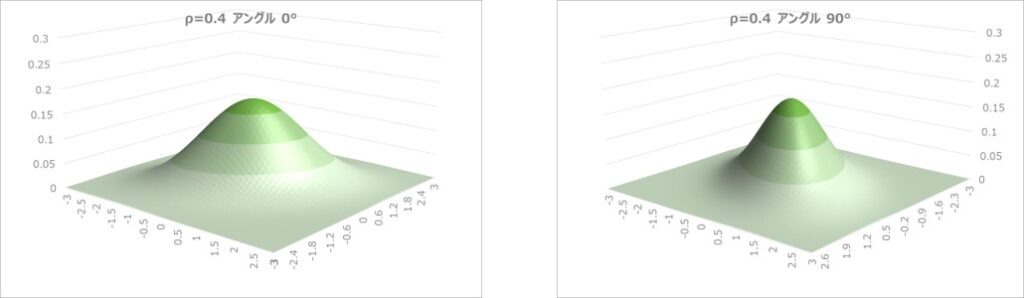
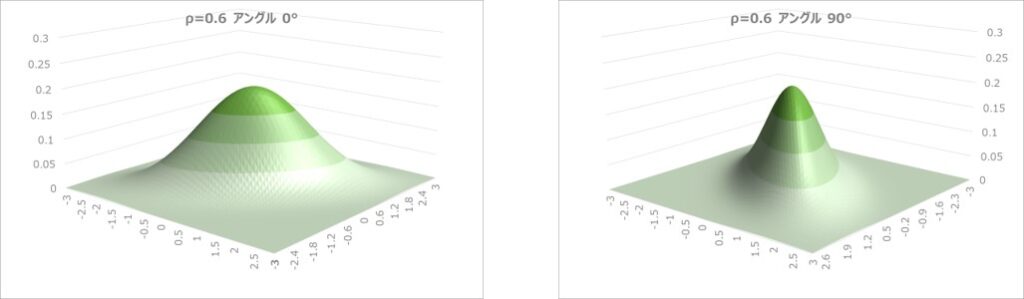
等高線グラフの数値データをマトリックスに表示すると以下のようになります。
$f(x,y)$の値の大きいほどコンター図の色を濃く表示しています。
このマトリックスの図からも分布の均等性の違いが見えますね。

まとめ
- 同時確率分布
⇒2つの確率変数$X$,$Y$を与えたときに、その発生確率を分布で表したもの
離散型:同時確率質量関数
連続型:同時確率密度関数 - 周辺確率分布
⇒同時確率分布において、確率変数のひとつを固定し、もう一つの変数における確率の総和を表したもの - 期待値
⇒$E(X+Y)=E(X)+E(Y)$
$E(X-Y)=E(X)-E(Y)$ - 共分散
⇒$Cov(X,Y)=E{(X-μ_x)(Y-μ_y)}$ - 分散
⇒$V(X+Y)=V(X)+V(Y)+2Cov(X,Y)$
$V(X-Y)=V(X)+V(Y)-2Cov(X,Y)$ - 二次元正規分布
⇒$X$,$Y$が独立の場合:面方向に均等な分布形状
$X$,$Y$が独立でない場合:面方向に偏りを持った分布形状
変数が一つ増えると頭の中で理解することが一気に難しくなりますが、一度、視覚的に捉えておくと、数式のパラメータがどのように影響するのかイメージしやすくなります。
エクセルで簡単に行列の計算をできるので、ぜひ一度試してみてください。





コメント