「確率分布の定義がよく分からない」
「確率分布の種類と特徴を教えて」
こんな疑問や悩みをお持ちの方に向けた記事です。
確率分布って名前を見るだけでも難しそうで、定義をあらためて確認することも敬遠しがちですよね。
しかし、確率分布は正規分布や二項分布などの基礎となる考え方で、統計学を学んでいく上では必要不可欠の知識です。
この記事では、統計学が初めての方でも理解できるよう、確率分布の定義、種類、その特徴について、わかりやすく解説していますので、参考になればうれしいです。
確率変数とは
まず最初に、確率変数について説明します。
JIS Z 8101-1によると、確率変数は以下のように定義されています。
どのような値となるかが、ある確率法則によって決まる変数。確率法則は確率分布で記述される。
引用元:JIS Z 8101-1:1999 統計-用語と記号ー第1部:確率および一般統計用語
つまり、値が一つに決まったものではなく、とある確率に従って決まる変数のことを意味し、一般的な表記としては、確率変数をX、その確率をP(X)と表します。
確率変数の一般的な例としては、サイコロの目があります。
サイコロの目は、1から6までの値があり、偏りがなければ全て1/6の確率でいずれかの値を取ります。
この場合、サイコロの目が確率変数Xであり、それぞれの目の発生確率P(X)は以下のように表されます。
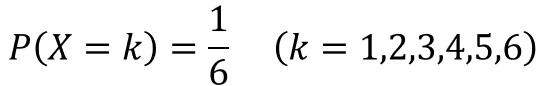
その他の例としては、コイン投げがあり、確率変数として表を1、裏を0とした場合に、以下のように記載されます。
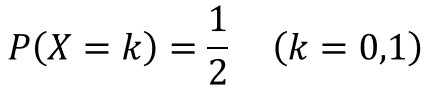
確率分布とは
同じくJIS Z 8101-1によると、以下のように定義されています。
確率変数がある値となる確率、又はある集合に属する確率を与える関数。その確率変数が定義されている集合全体に対する確率は 1 である。
引用元:JIS Z 8101-1:1999 統計-用語と記号ー第1部:確率および一般統計用語
つまり、確率変数とその発生確率の対応を表した分布を意味します。
先ほどのサイコロの事例で説明すると、1の目の確率は1/6、2の確率は1/6、3の確率は1/6・・・と、それぞれの変数に対応する確率が存在します。
このように、サイコロの目(確率変数)に対する発生確率の分布を表したものが確率分布となります。
そして、分布全体の合計値は、すべての確率変数の発生確率の合計になるので、必ず1になります。

出やすさを表したものってことだね
離散型確率分布
離散型とは、確率変数が不連続な値を取る分布のことで、先ほどのサイコロの目を始めとして、個数などの計数値が変数となります。
代表例としては、二項分布やポアソン分布があります。
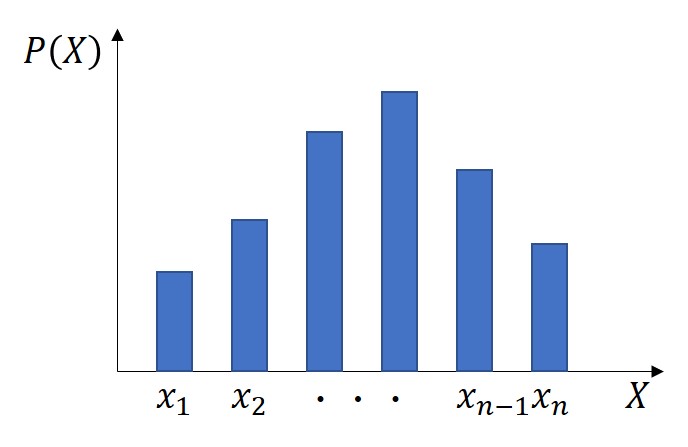
確率変数Xがある値xを取る場合の確率を関数にしたものを確率質量関数f(x)と呼びます。
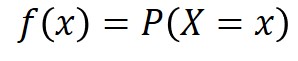
集合全体の確率の合計が1であることは、以下の数式で表されます。
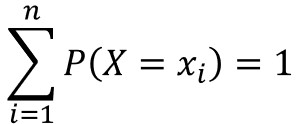

連続型確率分布
連続型とは、確率変数が連続的な値を取る分布のことで、長さや質量といった計量値が変数となります。
代表例としては、正規分布や指数分布があります。
離散型との違いとしては、確率変数の「点」での確率が存在しないことです。
例えば、サイコロの目の場合、1~6の6種類のいずれかに割り振られますが、長さの場合は、どうなるでしょう。
長さ1mの確率といっても、小数点以下をカウントした場合、0.999や1.001などは別の値になってしまいます。
そのため、ジャスト1mとピンポイントでの確率は存在せず、理論上では0ということになります。
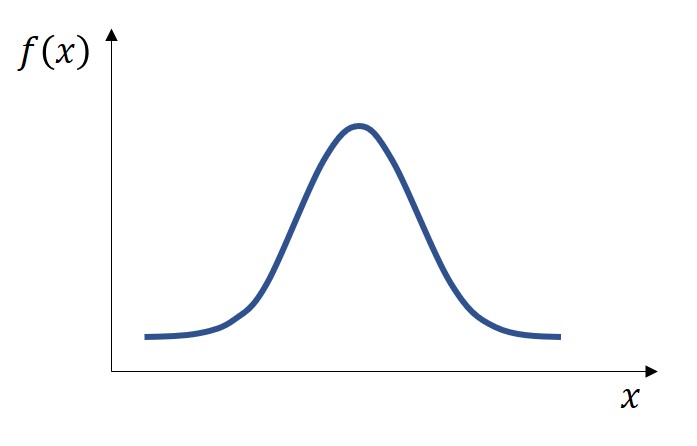
それでは、確率分布は全てゼロになるのかというと、それも間違いで、連続型確率分布では分布を示すf(x)に確率密度関数が用いられます。
確率密度関数とは、確率とは次元が異なりますが、発生のしやすさを関数に表したものであり、とある微小な確率変数の幅に対する発生確率のようなイメージのことです。
あくまでも相対的な発生のしやすさを表しているため、確率密度関数の値は1以上になることもあります。
なお、確率変数がマイナスの値や小数点以下の値も取るので、合計が1を示す数式は以下のように表されます。
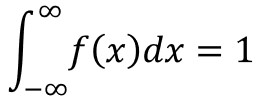

式の見た目は違うけど同じ意味を表しているんだね
まとめ
- 確率変数
⇒値が一つに決まったものではなく、とある確率に従って決まる変数 - 確率分布
⇒確率変数とその発生確率の対応を表した分布
⇒分布全体の確率の合計値は1になる - 離散型確率分布
⇒確率変数が不連続な値を取る分布で、確率質量関数を用いる
⇒二項分布やポアソン分布など - 連続型確率分布
⇒確率変数が連続的な値を取る分布で、確率密度関数を用いる
⇒正規分布や指数分布など
離散型と連続型の確率分布は、色々な種類に分かれる分布の基本に当たるので、しっかりと定義と特徴をおさえておきましょう。




コメント