「実験計画法って何を目的にした手法なの?」
「実験の種類にはどんなものがあるの?」
「実験計画を決める際の注意点を知りたい」
こんな疑問や悩みをお持ちの方に向けた記事です。
統計学に携わったことのある方やエンジニアの方であれば、一度は耳にしたことがある手法かもしれません。
しかし、名前を見るからにいかにも難しそうで、中身を見る前に敬遠してしまったという方も少なくないのではないでしょうか。
実験計画法はさまざまな書籍が発行されていますが、実験の手法が数多く、その分だけ内容も奥深いものですので、読み進めると専門的すぎてサッパリ・・なんてことも。
この記事では、高い専門性までは必要としていないけれども実験計画法の考え方だけ理解しておきたい、という方に向けて、できるだけ難しい表現を使わずに解説しています。
ぜひ参考にしていただければ幸いです。
また、Youtubeチャンネルでも実験計画法の基礎知識について解説していますので、あわせてご覧いただけると幸いです。
実験計画法の考え方
実験計画法とは?
実験計画法とは、ある因子の条件を複数の水準で変えて実験を行う際に、効率良く、かつ漏れのないようにデータを取得して、統計的に結果を判定する解析手法です。
英語では、DOE(Design of Experiments)と呼びます。
1920年代にイギリスの統計学者R.A.フィッシャーが農学分野での試験で適用して定着した手法で、現在は医学、工学など幅広い分野で活用されています。
例えば、とある製品の寸法が、製造過程の処理温度と圧力に影響を受けることが分かっているとします。
この寸法を狙い通りに制御するには、因子(温度と圧力)の条件を変えて寸法データを取得し、どの水準が最適か決めればよいことは直感的にもお分かりいただけると思います。
ただ、単純に寸法データを比較するだけでは、最適水準は選べたとしても、影響がどの程度なのか、因子どうしの相互作用はあるのか、定量的に解析することはできません。
また、水準の数が多くなった場合に、水準の組み合わせを総当たりで調べるには膨大な労力がかかりますし、だからといって適当に直感で水準を減らすわけにもいきません。
そこで、実験計画法の考え方を適用して、水準割り付けをルールに則って計画し、それぞれの因子の効果の大きさや相互作用を統計的に判定しようというものなのです。

考え方の基準があるのは助かるね
基本的な考え方は分散分析
実験計画法では、回帰分析と同じように分散分析の考え方を用います。
分散分析とは、その名の通り分散を分析して結果に意味があるのかどうか判定することで、「分散」というのは、水準間の分散と水準内の分散の2つを意味します。
ここで、実験計画法で扱う用語について整理しておきます。

分散が大きいということは、すなわち特性に与える影響が大きいことを表します。
そのため、水準間の分散(効果)が水準内の分散(誤差)よりも十分に大きければ、それだけ因子の影響が大きいことを意味しているのです。
そして、十分に大きいかどうかを判定するには、水準間と水準内の分散比をF検定することで、客観的な指標として評価することができます。

F分布とF検定については、以下の記事で詳しく解説していますので、あわせてご覧ください。


ちなみに回帰分析では、回帰変動(回帰式で説明可能な成分)と残差変動(誤差成分)を定義し、これらの分散比をF検定で判定しますので、基本的には同じ考え方です。
回帰分析については、以下の記事で解説しています。

フィッシャーの3原則
さて、ここまでの説明から実験計画法の目的と基本的な考え方についてご理解いただけたと思います。
次に紹介するのは、フィッシャーの3原則という考え方で、実験計画法とは切っても切れない関係にあります。
実験を行う場合のデータの取り方、順序などの注意事項としても関連しますので、ぜひ覚えておきましょう。
フィッシャーの3原則とは、次の3つで構成されます。
反復の原則
ひとつの水準につき、複数回のデータを取得することを意味します。
1回分のデータしか取得しなかった場合、その結果が系統誤差(誤差を生む要因がはっきりしたもの)か、偶然誤差(たまたま生じた誤差)なのか、区別できません。
そのため、たった1回のデータから判断すると真実を見誤る可能性があり、どうしても複数回の実験ができない制約がある場合を除いて、反復試行することが原則です。
無作為化の原則
データを取得する際はランダムに抽出することを前提とする原則です。
例えば、1日で3水準の実験を2回行い、これを3日間繰り返したとします。
6回のデータを毎日同じ順序で取った場合、1日のうちの時刻による影響を受けてしまう可能性があります。
一例として気温のような外乱の因子が考えられ、気温の変動に影響を受ける実験では順序を日ごとに変えることが必要です。
このような場合には、日ごとに水準の順番をランダムに変えて実験を行うことが必要となります。
局所管理の原則
実験の順序、場所、時間などが特性に影響を及ぼす場合、これらの要因を同じ条件に固定することを局所管理と呼びます。
条件をそろえることで系統誤差の影響を小さく抑えられることから、比較したい対象の因子の影響が見えやすくなります。
先ほどの気温の例を用いると、そもそも気温が特性に影響を与えるのであれば、毎日同じ時刻にデータを取得すれば、一日の寒暖差の影響を受けなくなります。
さらには、データを取得する場所もそろえれば、外乱となる因子を一層と排除でき、さらに対象因子の影響が分かりやすくなります。
このように、条件をできるだけ統一して小さい単位で管理することが、局所管理の原則なのです。

屋外環境はばらつきが多いから特に注意しよう
余談(制御因子と誤差因子)
フィッシャーの3原則を紹介しましたが、これらを忠実に守って実験計画を立てようとすると、現実問題として成立しない場面に直面します。
例えば、毎日同じ時刻にデータを取得しようとしても、必ずしも作業者の予定を空けられるわけではありませんし、実験にかかる期間も非常に長くなってしまいます。
いくら現実味のない計画を立てても単なる絵に描いた餅になってしまうので、時間、お金、人の制約を踏まえた上で、きちんと完遂できる計画を立てる必要があります。
重要なのは、計画を立てる自分自身が、特性に影響する因子を漏れなく把握できているかどうか、その因子を性質によって分類して整理できているかどうか、ということです。
品質工学の用語を用いると、特性に影響を与える因子は次のように分類されます。
制御因子:最適条件を知ることを目的とするものであって、水準を自らが設定する因子(加工時の温度、圧力、時間など)
標示因子:最適条件を知ることが直接の目的でないが、局所管理の原則にもとづいて実験の際に一時的に水準を決めるべき因子(時刻、室温など)
誤差因子:水準を自らが制御できない因子(外気温、湿度など)
実験の目的や環境の前提によって、どの項目がどの因子に分類されるか変わってきますので、自身のケースに当てはめて因子を抽出して分類しましょう。
そして、現実的な問題としてどうしても3原則を準拠できない場合には、どの因子がばらつきとして含まれるのか承知した上で計画を立てることが望ましいです。
特性に影響を与える要因の抽出にあたっては、QC7つ道具のひとつ特性要因図を用いると、視覚的にも分かりやすく整理できますので、おススメです。

実験の主な種類
さて、最後に実験計画法における実験の種類について説明します。
水準の組み合わせ通り数の考え方から、大きく次の2つに分類できます。
要因配置実験:水準の組み合わせを総当たりで行う実験
部分配置実験:一部の水準の組み合わせを行う実験

要因配置実験
水準の組み合わせを総当たりで行う実験で、因子が一つの場合を一元配置実験、二つの場合を二元配置実験、三つ以上を多元配置実験と呼びます。
例えば、二元配置実験の場合、因子Aを3水準、因子Bを2水準、繰り返し回数を2回とすると、3×2×2=12回の実験が必要になります。
組み合わせの通り数を掛け算で求められるので、感覚的にも理解しやすいですね。
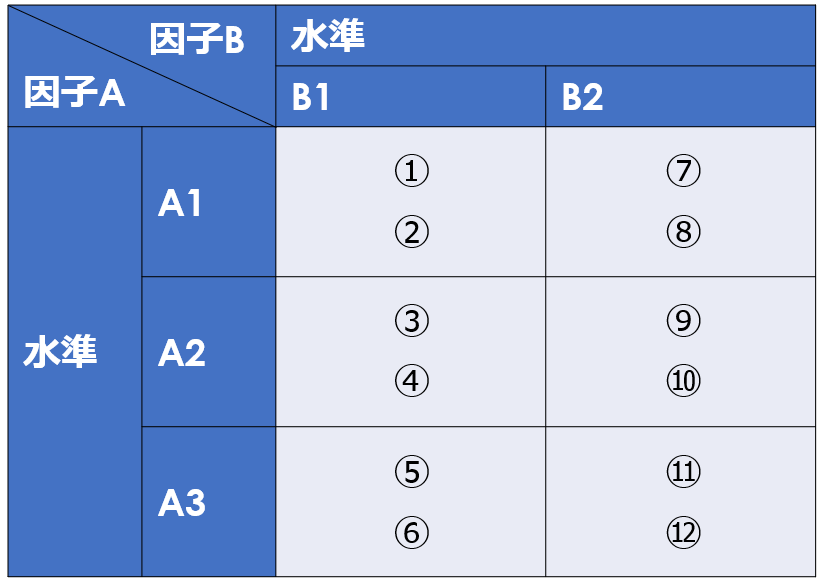
要因配置実験のメリットとしては、総当たりで実験を行うため、因子どうしの比較がしやすい点です。
例えば、因子Bの影響を比較したい場合、因子Aの条件が同じものどうしを見れば、単純比較することができます。
デメリットとしては、総当たりでの実験が必要なため、時間とコストがかかる点です。
因子数の掛け算で通り数が決まるため、因子が3つ以上になると膨大な量となってしまいます。
部分配置実験
一部の水準の組み合わせで実験を行うもので、代表的な手法として直交表実験があります。
直交表は、因子を列、実験番号を行に配置し、行と列の交差する箇所に水準の条件(例えば2水準の場合、1または2)を記載した表です。
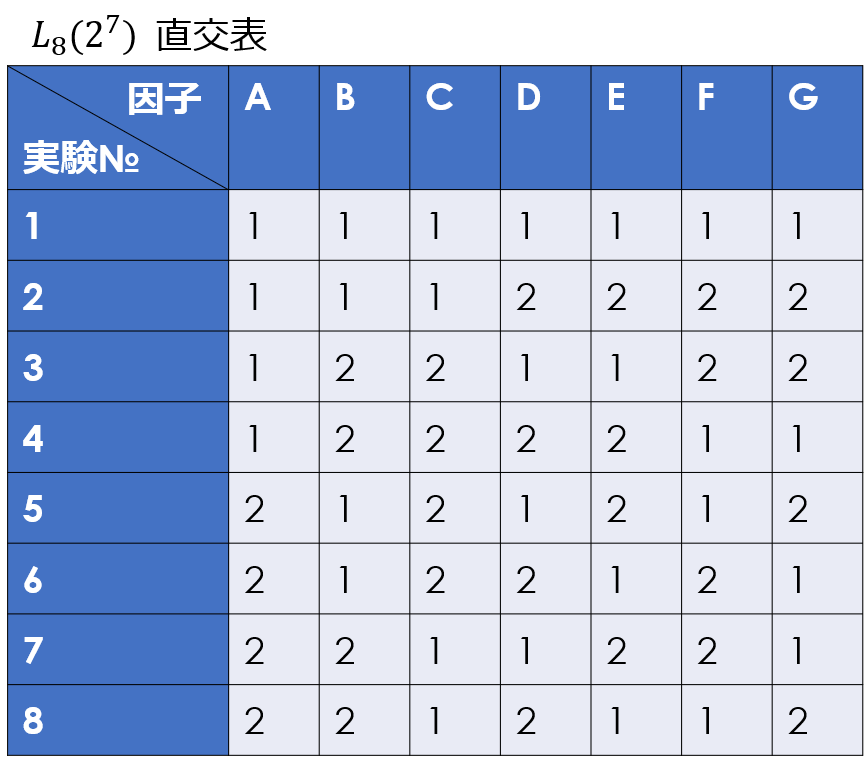
各実験での水準の条件は、行の方向に読み取れば良く、上記の表の例でいうと、例えば実験2では、因子A~Cは水準1、因子D~Gは水準2で実施すれば良いことが分かります。
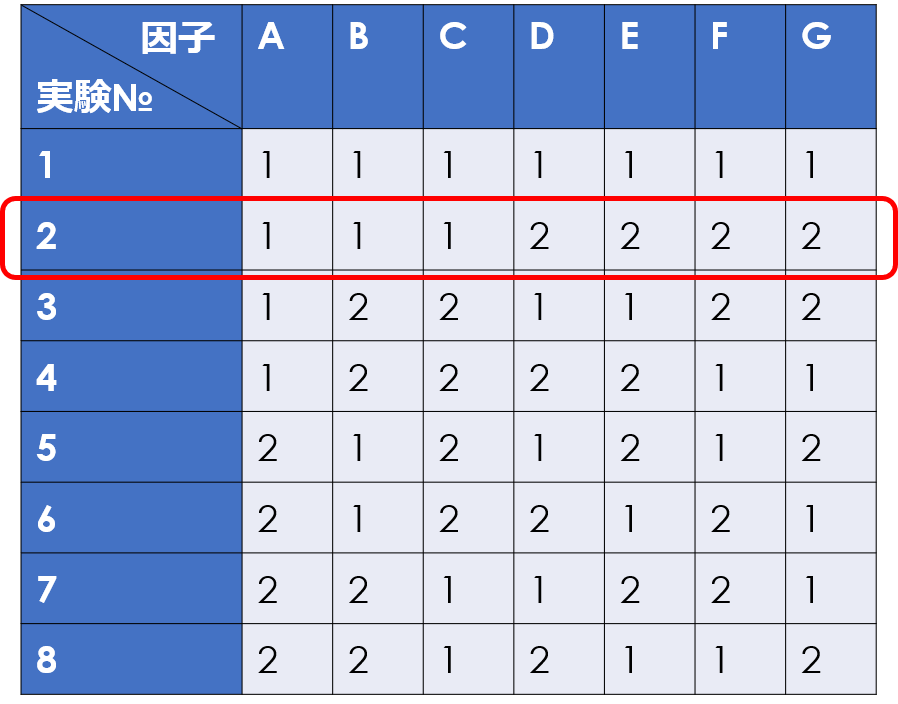
今度は列方向に着目してみると、各列の水準の組み合わせが同じ回数現れることが分かります。
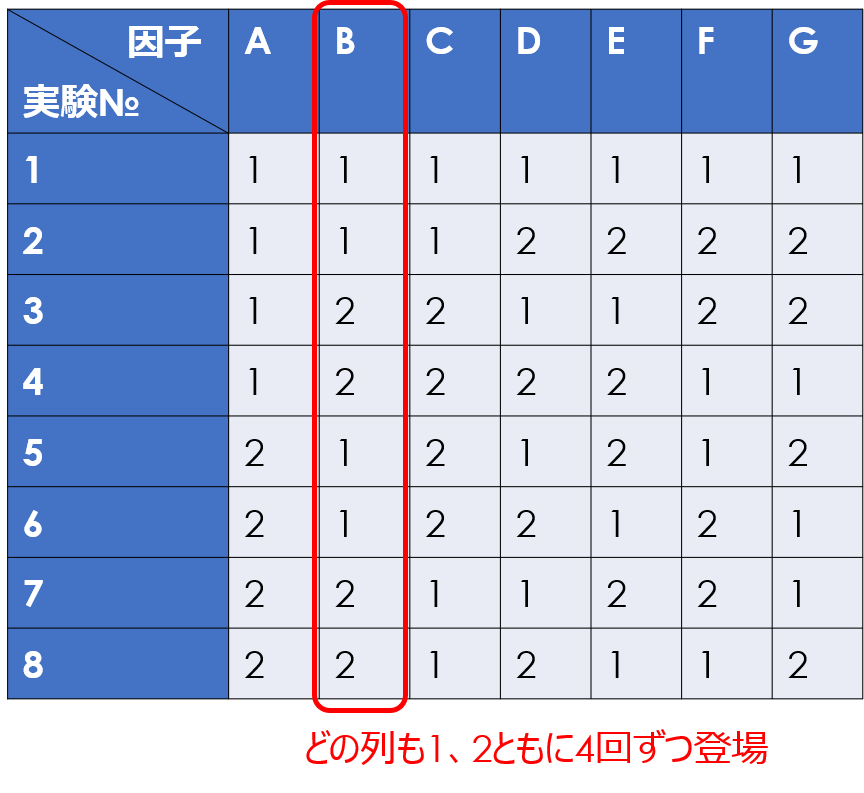
この状態を「直交している」と表現し、特定の水準に偏ることなく均等な割り付けが可能で、かつ評価の組み合わせ通り数を大幅に削減できる特徴があります。
例えば、先ほどの例で示したL8直交表では、7つの因子を2水準で評価するので、総当たりでは2の7乗で128通りの実験が必要ですが、直交表ではなんと8通りで良いのです。
実験の負荷を大幅に減らせることが部分配置実験の最大のメリットで、L8直交表以外にも3水準に対応したL9直交表、15の因子に対応したL16直交表など多くの様式があります。
一方、デメリットとして注意しておきたいのが、あらかじめ因子どうしの交互作用の有無を把握しておかなければならない点です。
交互作用の影響の大きさを調べるために実験をやろうとしているのに、あらかじめ関係の有無が分かっているなんて、何とも矛盾しているように見えますね。
しかし、組み合わせ通り数を削減した影響で、総当たり実験のように因子どうしを一つずつ単純比較できず、あらかじめ直交表に割り付けた因子間の交互作用しか見られません。
そのため、例えば別々の工程の因子のように交互作用のないことが自明なものを直交表から外すなど、作成者が意思を持って割り付けを決めていく必要があります。
あるいは、交互作用を調べるために直交表実験とは別の予備実験を行うのも有効です。
いずれにせよ、機械的に直交表に割り付けて実験するだけで、情報量を損なわずに負荷も減らせるなんていう魔法のツールは存在しません。
実験を計画する側がきちんと理屈を考えて着目すべき因子を絞り込むことによって規模を削減できる効果が得られる背景を忘れないようにしておきましょう。

ツールに頼りきらず結局はしっかり自分で考えようってことね
まとめ
- 実験計画法(DOE:Design of Experiments)
ある因子の条件を複数の水準で変えて実験を行う際に、効率良く、かつ漏れのないようにデータを取得して、統計的に結果を判定する解析手法 - 実験計画法の基本的な考え方
分散分析の考え方を適用し、水準間の分散(効果)と水準内の分散(誤差)の比をF検定により判定する - フィッシャーの3原則
①反復の原則
②無作為化の原則
③局所管理の原則 - 要因配置実験
水準の組み合わせを総当たりで行う実験
実験の規模は大きいが主効果と交互作用を詳しく調べられる - 部分配置実験
一部の水準の組み合わせを行う実験
全ての交互作用は検証できないが実験の規模を大幅に削減できる
代表的な手法として直交表実験がある
最後までご覧いただきありがとうございました。
数式の苦手な方でも安心の入門編。
回帰分析、検定、実験計画法まで幅広く、エクセルを用いた実践方法も習得したい方に。
乱塊法、分割法もお任せ! QC検定1級の教材としてもおススメ。




コメント