「F分布ってどういう分布なの?」
「どのような使い道があるの?」
「エクセルやF分布表で実際に確率を求めたい」
このような疑問や悩みをお持ちの方に向けた記事です。
F分布とは、2つのカイ二乗分布に従う確率変数の二乗和χ2値をそれぞれの自由度で割って比で表したF値が従う確率分布のことです。
この記事では、F分布の定義と性質、活用の用途、期待値と分散の導出の仕方、エクセルやF分布表から確率を求める手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
F分布とは?
定義
最初にF分布の定義について説明します。
F分布とは、2つのカイ二乗分布に従う確率変数の二乗和χ2値をそれぞれの自由度で割って比で表したF値が従う確率分布のことで、「F」は統計学者のフィッシャーに由来しています。
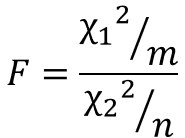
χ2はカイ二乗値、mは第一自由度、nは第二自由度を表します。
まず、F分布を学習する前の予備知識として、カイ二乗分布を理解しておく必要がありますので、合わせてご覧ください。

カイ二乗分布は、標準正規分布N(0,1)を基にした確率変数の二乗和が従う確率分布で、母分散の区間推定や分散の差に関する検定などに活用されます。
F分布でも「ばらつき」「分散」に関わる性質を表すことには変わりませんが、F分布では2つの集団における分散の比を扱うことがカイ二乗分布と異なります。

カイ二乗分布と間違えやすいから注意しよう
確率密度関数
F分布の確率密度関数は以下の数式で定義されます。
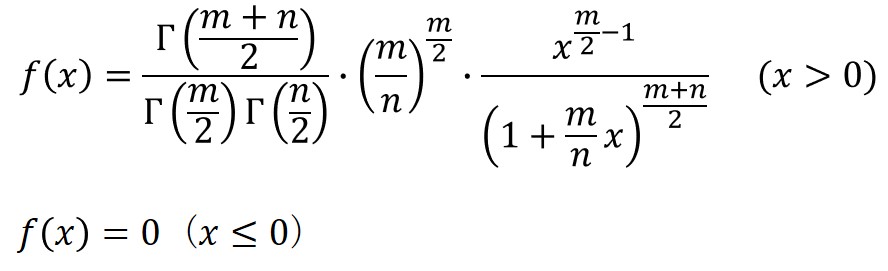
F分布の特徴は、2つの自由度から分布の形状が決まることです。
Γ()はガンマ関数を意味します。
ガンマ関数とは、階乗の概念を表す特殊な関数で、Γ(n)=(n-1)!として定義されます。
数式が非常に難解ですが安心してください、覚える必要はありません。
後ほど説明するエクセルの関数やF分布表を用いれば、複雑な計算式を解かなくても、簡単に確率を求めることができます。
なお、確率密度関数については、別の記事で詳しく紹介していますので、合わせて参考にしていただければと思います。

F分布の性質
逆数のF分布
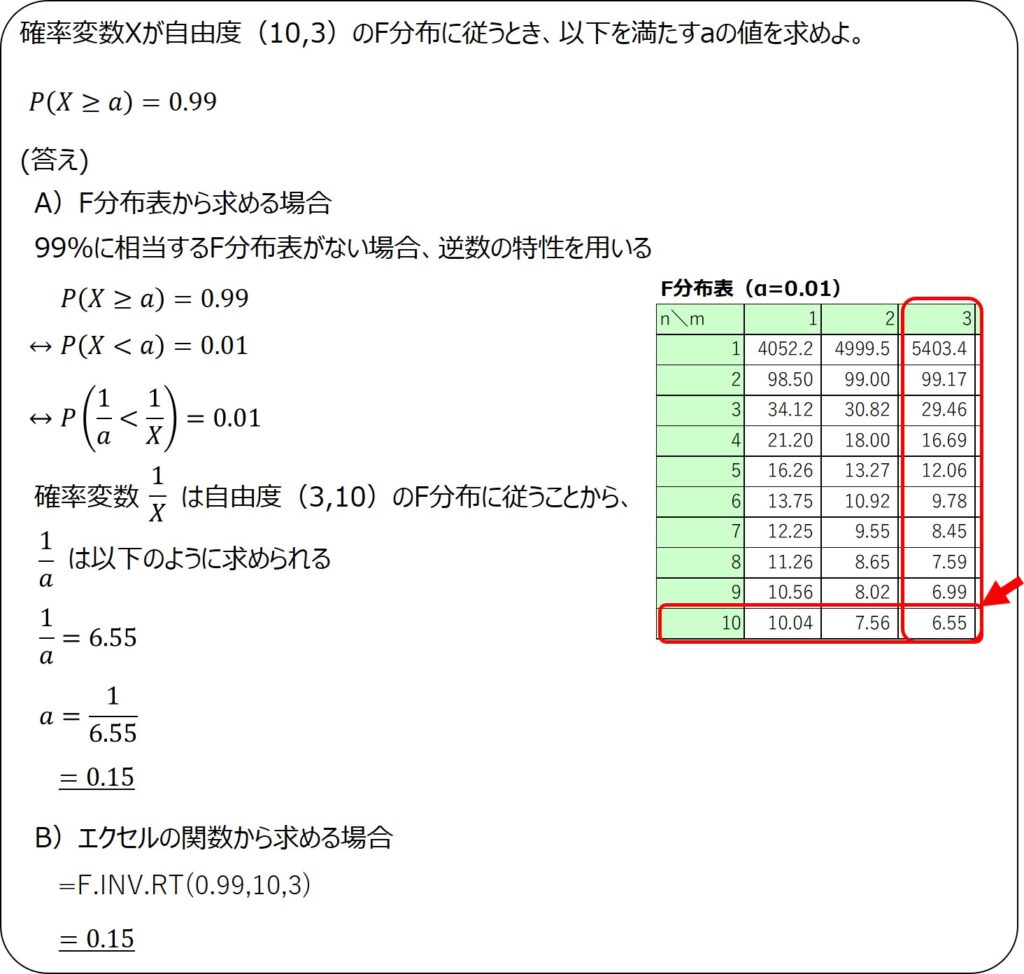
確率変数Xが自由度(m,n)のF分布に従うとき、確率変数の逆数1/Xは自由度(n,m)のF分布に従います。
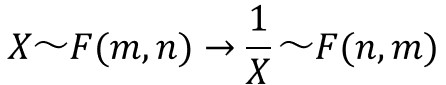
これは後ほど説明するF分布表を用いて上側(右側)確率を求める際に活用できる性質です。
F分布表では、一般的に5%や1%の上側確率に該当するF値が記載されています。
しかし、逆に95%や99%に該当する確率を求めたい場合には、これらの表から値をそのまま読み取るだけではいけません。
このような場合に上記の性質を用いれば、自由度を入れ替えて確率変数の逆数を取ることで、下側確率に変換できるのです。
活用の用途
母分散の比の検定
母分散の比の検定(F検定)とは、ある2つの標本調査の結果から求めた母分散が等しいと言えるか、否かを調べるための検定手法のことです。
母分散の比を統計量とすると、この値はF分布に従うので、確率の計算で等しいか否か求めることができます。

「2つの母分散の比」をキーワードに覚えておこう
期待値と分散の導出
F分布における期待値E(X)と分散V(X)は、以下となります。
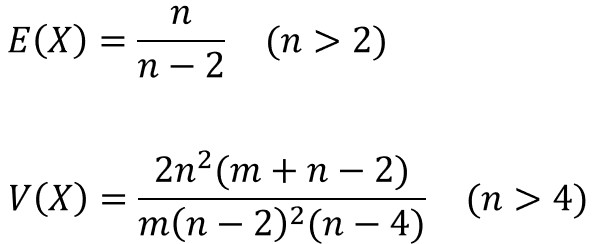
計算が複雑ですが、導出過程に興味のある方は参考にどうぞ。






なお、E(X)とV(X)の意味、V(X)の導出の過程については、別の記事で解説していますので、合わせてご覧ください。

エクセルでのグラフの書き方
エクセルでのF分布の確率の求め方、グラフの書き方を紹介します。
F.DIST関数を用いれば、確率密度関数を計算することができます。
DISTというのは、分布(distribution)の略で、F分布のFを繋げた名前が関数名になっています。
使い方は簡単で、次の4つの変数を指定するだけです。
①:F値(x)
②:自由度1(m)
③:自由度2(n)
④:関数形式(TRUE or FALSE)
④の関数形式については、確率密度関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
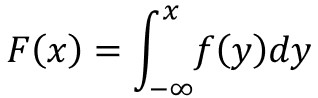
例えば、自由度m=3、n=20として、確率密度関数f(x)を求めると以下のようになります。
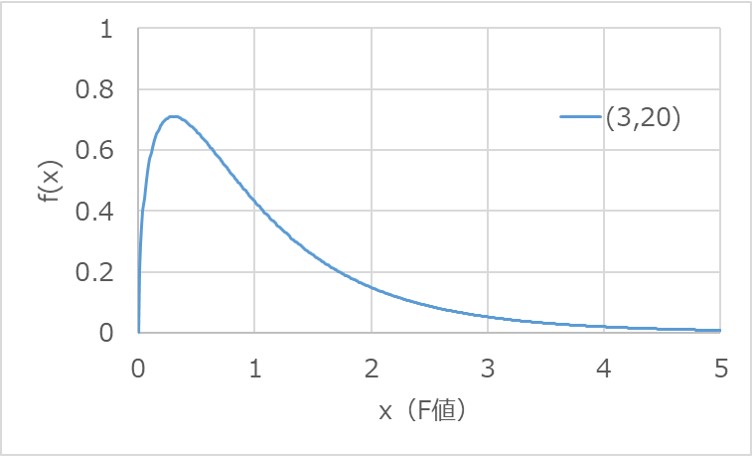
第一自由度と第二自由度を入れ替えると分子と分母の値が変わるので、f(x)の値も変わってきます。自由度の設定を間違えないように注意しましょう。
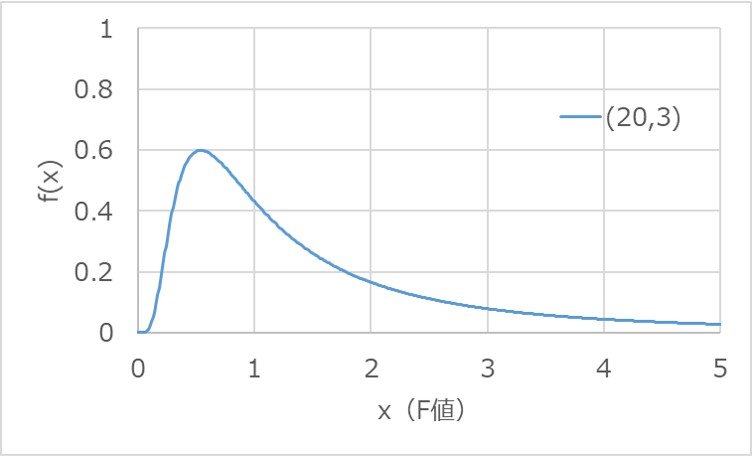
また、同様に自由度m=3、n=20における累積分布関数F(x)を求めると以下になります。
累積分布関数は、確率変数xの値が大きくなるにつれて、1に収束することが見て取れます。
これは、確率の合計値が1になることを表しており、この性質がグラフからも分かります。
なお、エクセルではF.DIST.RT関数と呼ばれるものもあります。
累積分布関数F(x)は、確率変数がある値以下として定義されますが、F.DIST.RT関数はある値以上の確率を表しており、つまり、以下の数式をこの関数で直接計算できるのです。
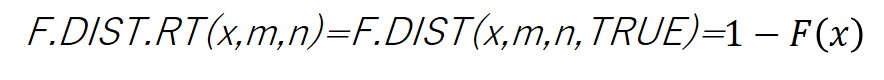
これは、F分布を用いた検定や推定を行う際に、F値がある値以上になる確率を求める場合も多いため、関数として用意されている訳です。

数式は難しかったけどエクセルだと簡単
F分布のグラフの特徴
右側に裾広がりの形状を示す
F分布のグラフは左右対称ではなく、右側に裾広がりの形状を示します。
以下のグラフは、自由度の違いによる確率密度関数の形状の違いを表したものです。
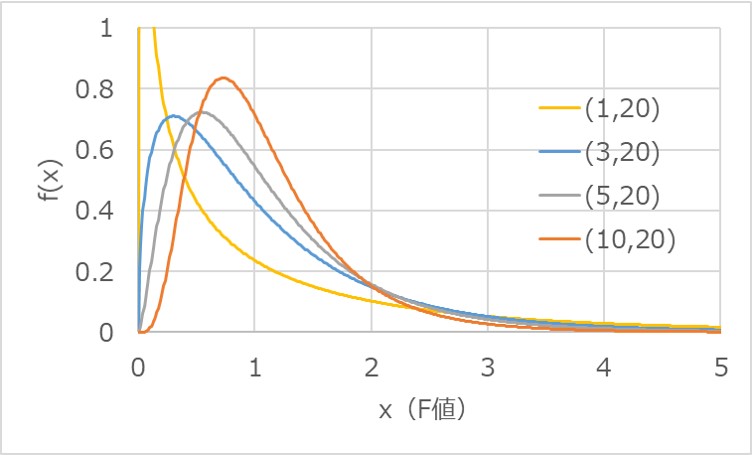
いずれも、右側に広がった分布を示していることが分かります。
また、自由度の増加にともない、ピークの中心が右側にシフトしていきます。
自由度が無限大で1を中心に分布
F分布の自由度を大きくして極限を取ると、1を中心に左右対称の形状に近づく性質があります。
以下は、自由度(100,100)におけるF分布のグラフです。
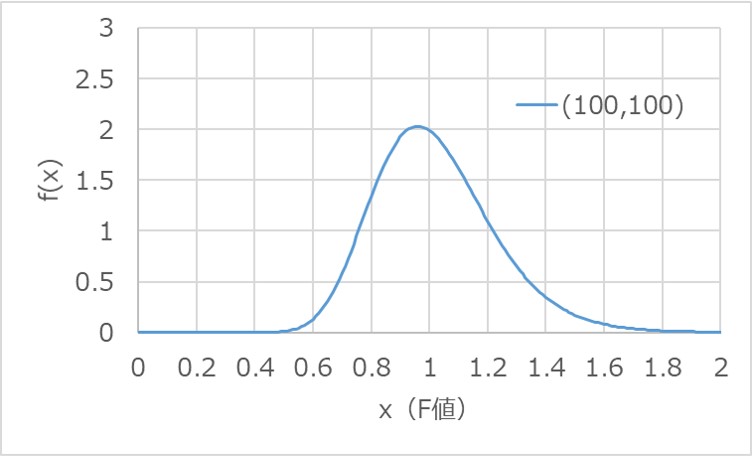
ほぼ正規分布に近い形状を示すことが分かると思います。
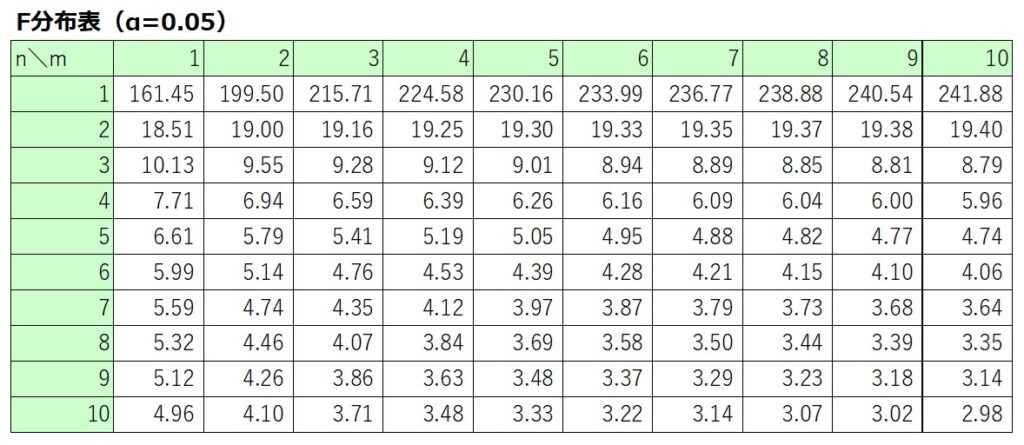
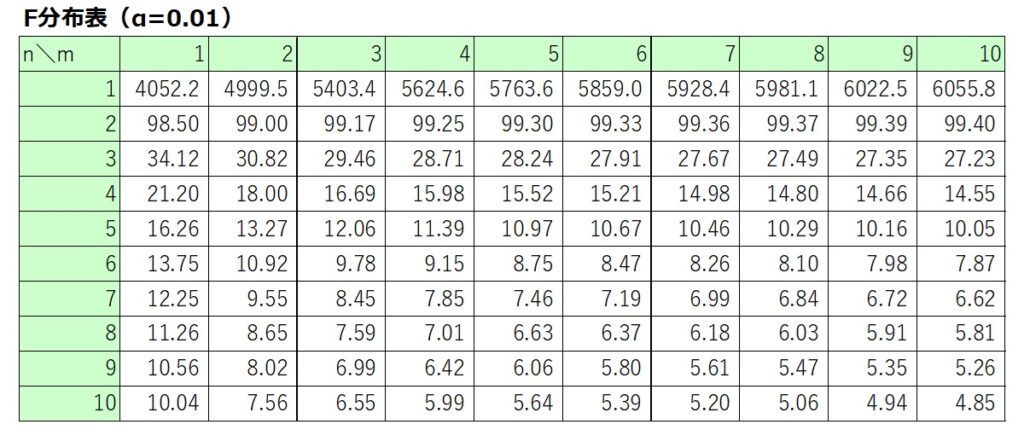
F分布表の読み方
F分布表とは、横軸に第一自由度m、縦軸に第二自由度nを取って、マトリックスの交差する箇所に対応するF値が記載されている表です。
上側(右側)確率αの値によって対応するF値は異なるため、一般的にα=0.05、0.01に該当するF分布表が与えられています。
例えば、上側確率α=0.05、自由度m=3、自由度n=5におけるF値は5.41と読み取ることができます。
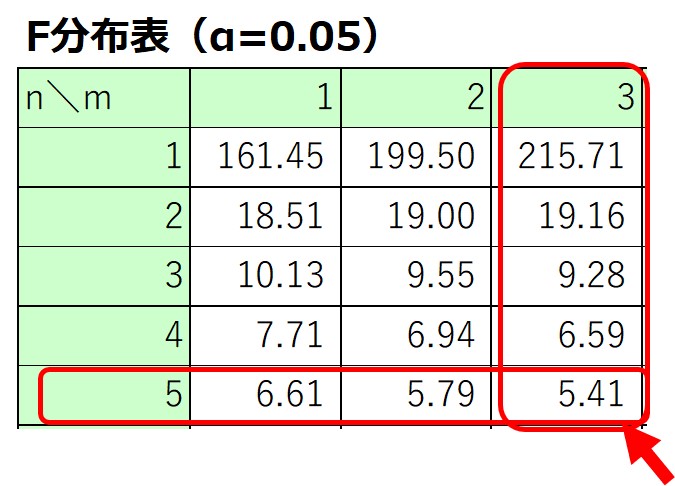
この他、α=0.025や0.005が使われることもあります。
なお、エクセルを用いて自分でF分布表を作る場合は、F.INV関数を用いると簡単に計算することができます。
これは、F分布の確率の逆関数を求めるもので、自由度と確率を指定すれば、対応するF値を計算できるのです。
一つ注意点としては、F.INV関数は下側(左側)確率の逆関数なので、上側(右側)確率に対するF値を求める場合には、確率を1-pとして計算する必要があります。
あるいは、上側確率を直接指定したい場合には、F.INV.RT関数を用いると良いでしょう。

例題
まとめ
- F分布
⇒2つのカイ二乗分布に従う確率変数の二乗和χ2値をそれぞれの自由度で割って比で表したF値が従う確率分布 - 活用の用途
⇒母分散の比の検定 - 期待値と分散
⇒期待値:n/n-2、分散:2n^2(n+m-2)/m(n-2)^2(n-4)(m,nは自由度を表す) - エクセルでの求め方
⇒F.DIST関数で、確率密度関数と累積分布関数を計算できる - F分布のグラフの特徴
⇒右側に裾広がりの形状を示す
自由度が無限大で1を中心に分布 - F分布表
⇒横軸に第一自由度m、縦軸に第二自由度nを取り、マトリックスの交差する箇所に対応するF値が記載された表
F分布は定義の概念を感覚的に捉えるのが難しいですが、一度、エクセルを使って自分でやってみると計算の意味や数値の感覚を理解できて、ハードルが下がるものです。
ぜひ使い方を覚えて、実務で活用できるようにしておきましょう。




コメント