QC検定2級の受検をお考えの皆さま、試験対策は順調に進んでいますか?
この記事では、2級の中でも頻出の統計的検定について、過去問の出題傾向と押さえておきたいポイントを紹介しています。
さらに、模擬問題と解説を合わせて掲載していますので、ぜひ参考になればうれしいです。
また、Youtubeチャンネルでは模擬問題の解説に加えて、統計的検定の基礎知識についても動画で解説していますので、あわせてご覧いただけると幸いです。
過去問の出題傾向
2018年から2021年までの6回の試験のうち、統計的検定は5回で出題される最頻出分野の一つです。
避けては通れないことが感じ取れる一方で、片側検定や両側検定、統計的検定のベースとなっている背理法の考え方など、苦手意識を持っている方も少なくないかと思います。
しかし、いろんな種類の検定方法がある中でも、基本的な考え方と計算式の定義を理解しておけば、いずれも同じ手順で解けるので、実は覚えることはそれほど多くありません。
むしろ、要所だけ押さえれば問題文を深く読み込む時間もかなり短縮できるので、ぜひ得点源とできるようにしておきましょう。
基本的に大問の構成は検定の手順に沿って穴埋め形式で記載されており、それぞれの小問の内容としては、大きく以下に分かれます。
- 帰無仮説または対立仮説を選ぶ問題
- 検定統計量を求める、または計算式を選ぶ問題
- 付表から棄却限界値を読み取って判定する問題
- 棄却・採択の結果から検定の結論を選ぶ問題
押さえておきたいポイント3選
統計的検定では区間推定と同じく、母集団から抜き取った標本サンプルの確率分布をもとにしています。
そのため、押さえておきたいポイントは基本的に区間推定と同じで、確率の取り方に細心の注意を払う必要があります。
その1:片側検定と両側検定の確率の取り方に注意
問題を解く際に真っ先に考えるべきは、どの種類の検定について問われているかということです。
検定の種類とは、母平均、母分散、母不適合品率など「検定統計量の種類」に関するものと、片側検定か両側検定なのか「対象とする確率の種類」に関するものの両方を意味します。
つまり、問題文を読んだら、まずは「母平均に関する片側検定」といったように検定の種類を読み取ることが必要で、これができてないと当然その後の計算も進められません。
片側検定と両側検定の概念を以下に示します。

文字通り、分布の「片側」「両側」を意味しており、例えば有意水準5%といっても片側検定の場合は片側に5%を取った状態、両側の場合は2.5%ずつを取った状態を表します。
また、検定統計量の種類について一覧を示します。
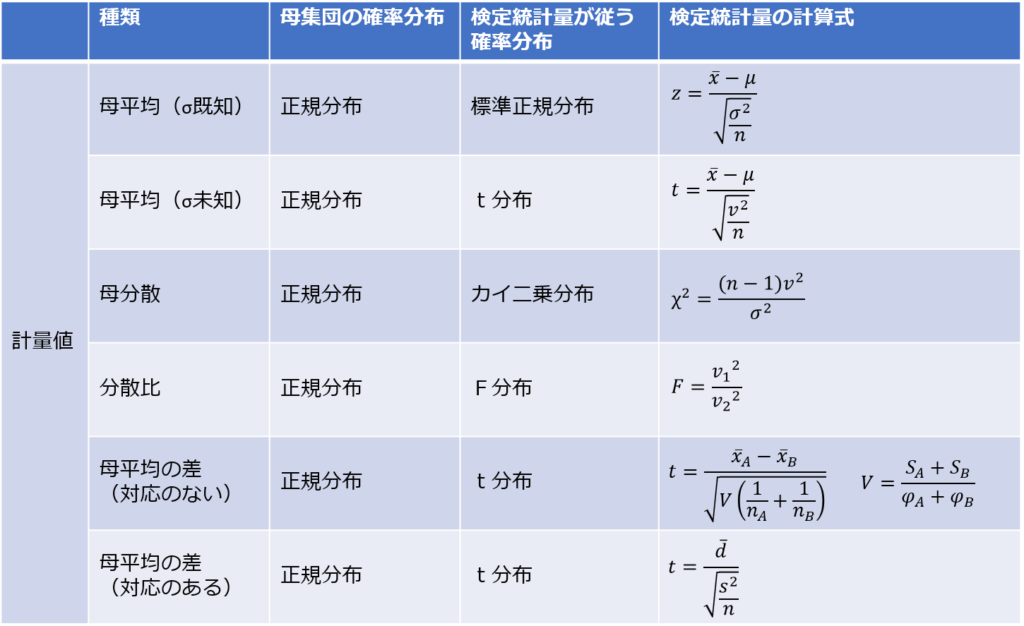
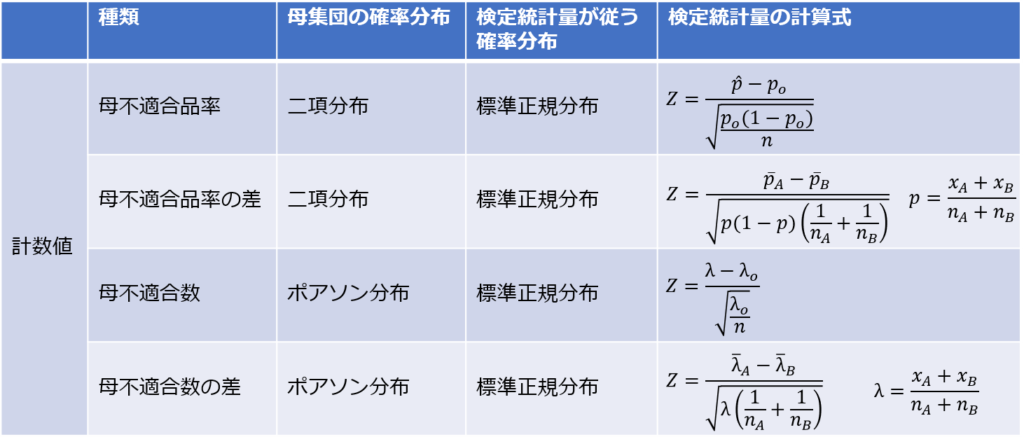
検定統計量が従う分布には、標準正規分布、t分布、カイ二乗分布、F分布があり、いずれも与えられた付表から対応する確率を読み取ります。
ここで注意の必要なのが、標準正規分布、カイ二乗分布、F分布は上側確率として定義されていますが、t分布は両側確率である点です。
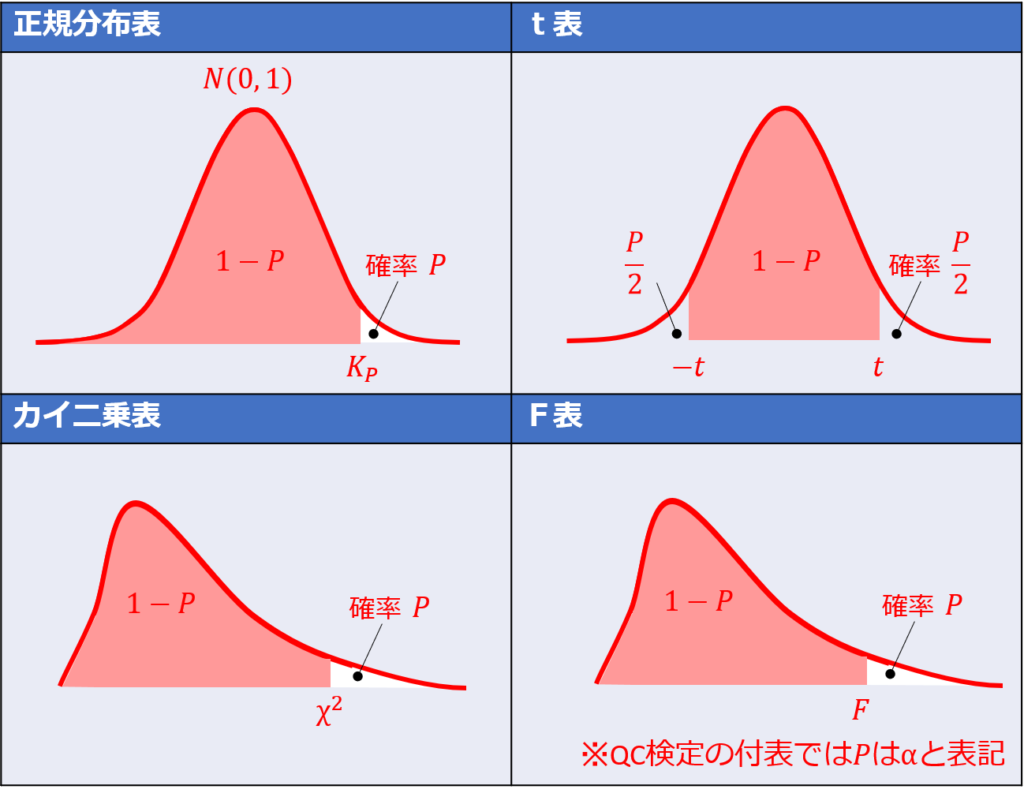
そのため、上側2.5%確率を読み取る場合でも、標準正規分布ではそのまま2.5%点、t分布では5%点(片側2.5%ずつ)と異なるので間違えないようにしましょう。
その2:検定統計量の符号に注意
両側検定の場合は、上側確率と下側確率を均等に分けて同時に判定するので、検定統計量の絶対値を用います。
例えば、検定統計量が棄却限界値に値して小さい場合は帰無仮説を採択、棄却限界値よりも大きい場合は帰無仮説を棄却(対立仮説を採択)します。
一方、片側検定の場合、上側確率の考え方は両側確率と同じで、棄却限界値よりも大きい場合に帰無仮説を棄却するので、見誤る可能性は低いと思います。
しかし、下側確率を対象にする場合には正負が反転するので、棄却限界値よりも値の小さい場合に帰無仮説を棄却することになります。
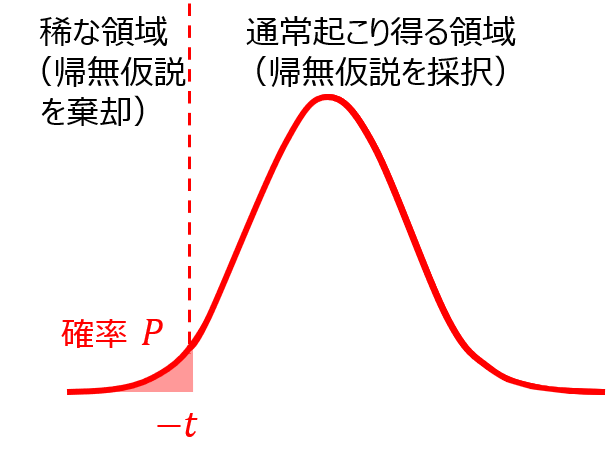
検定統計量の絶対値が大きいほど確率として起きにくいことを意味するので、両側確率も片側確率も考え方は同じですが、不等号を選ぶ問題では大小関係に注意しておきましょう。
その3:式の基本形はほぼ同じ
区間推定の記事でも紹介した通り、母平均、不適合品率、不適合数の検定いずれも式の基本形がほぼ同じです。
これは、正規分布$N(μ, σ^{2})$の母集団から抜き取った標本平均は$N(μ, σ^{2}/n)$に従う考え方にもとづいています。
分散$σ^{2}/n$は、すなわち標準偏差$\sqrt{σ^{2}/n}$を意味し、まさに$K_{p}\sqrt{V/n}$は標準偏差が何個分の幅に該当するか、ということを表しています。
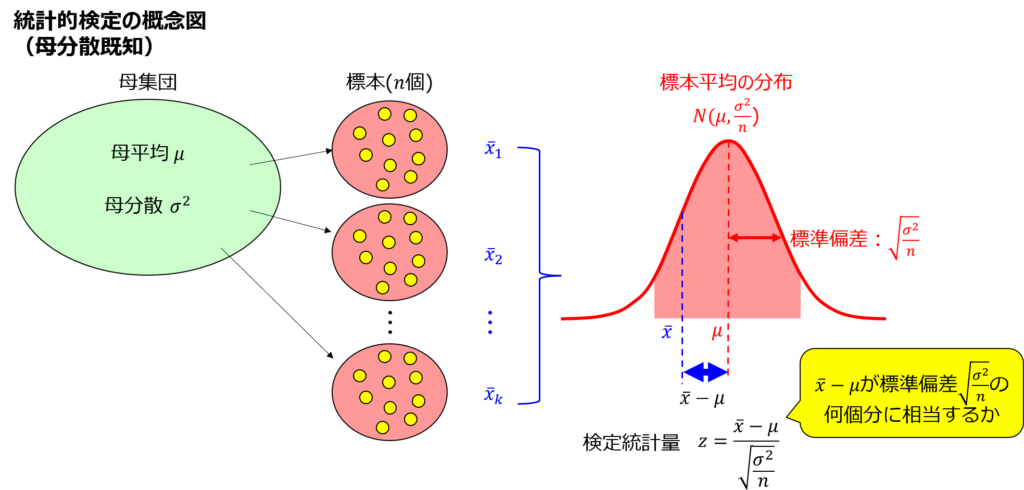
これは母平均の統計的検定に限らず母平均の差や母不適合品率にも当てはまるので、式の意味を理解しておけば、あとは分散の計算式を覚えるだけで検定統計量を導出できるわけです。
模擬問題
統計的検定に関する練習問題を6つ用意しました。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題1
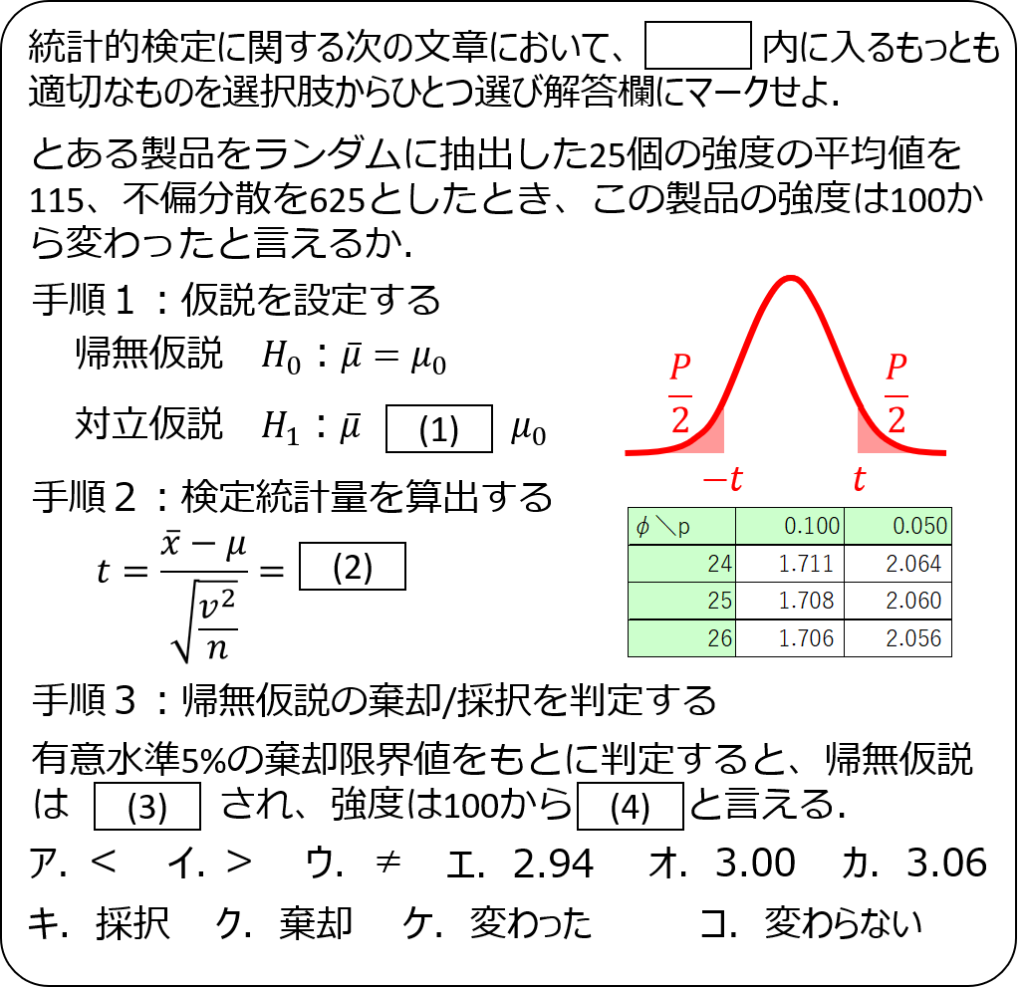
問題2
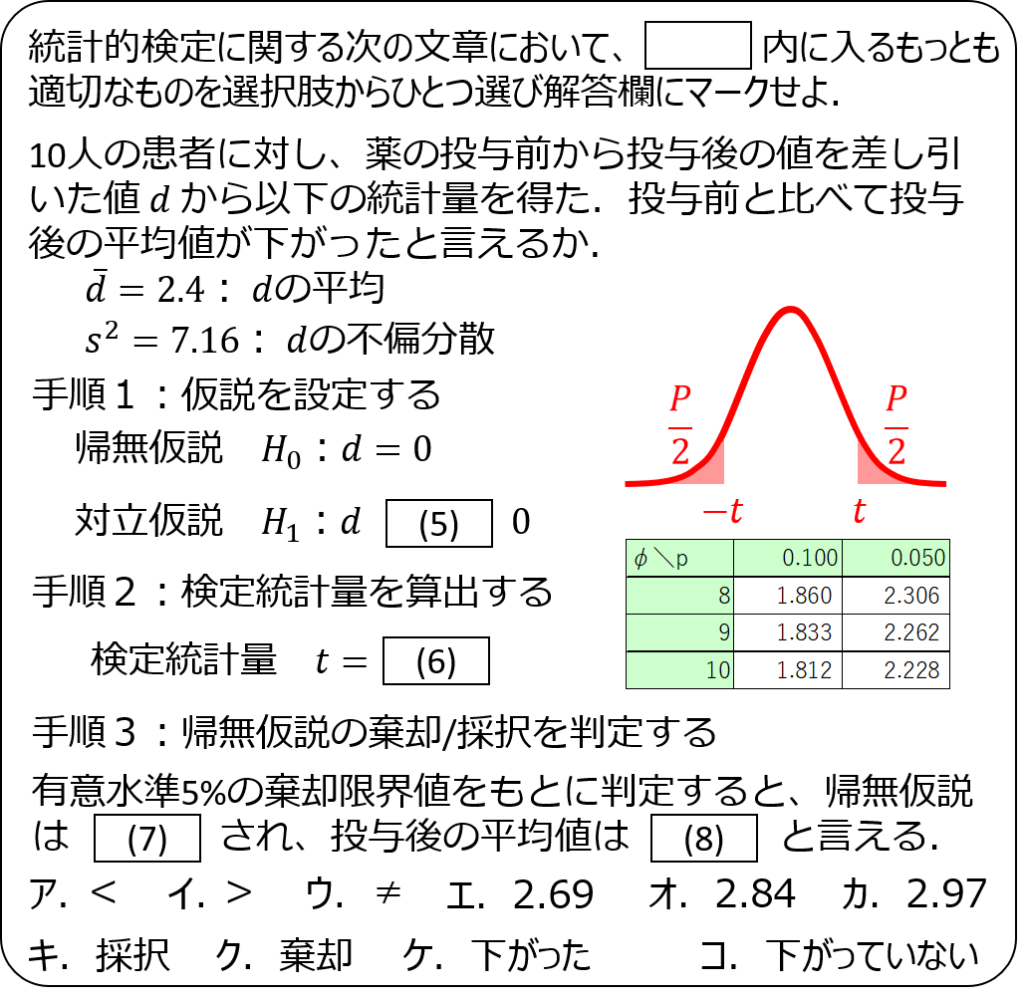
問題3
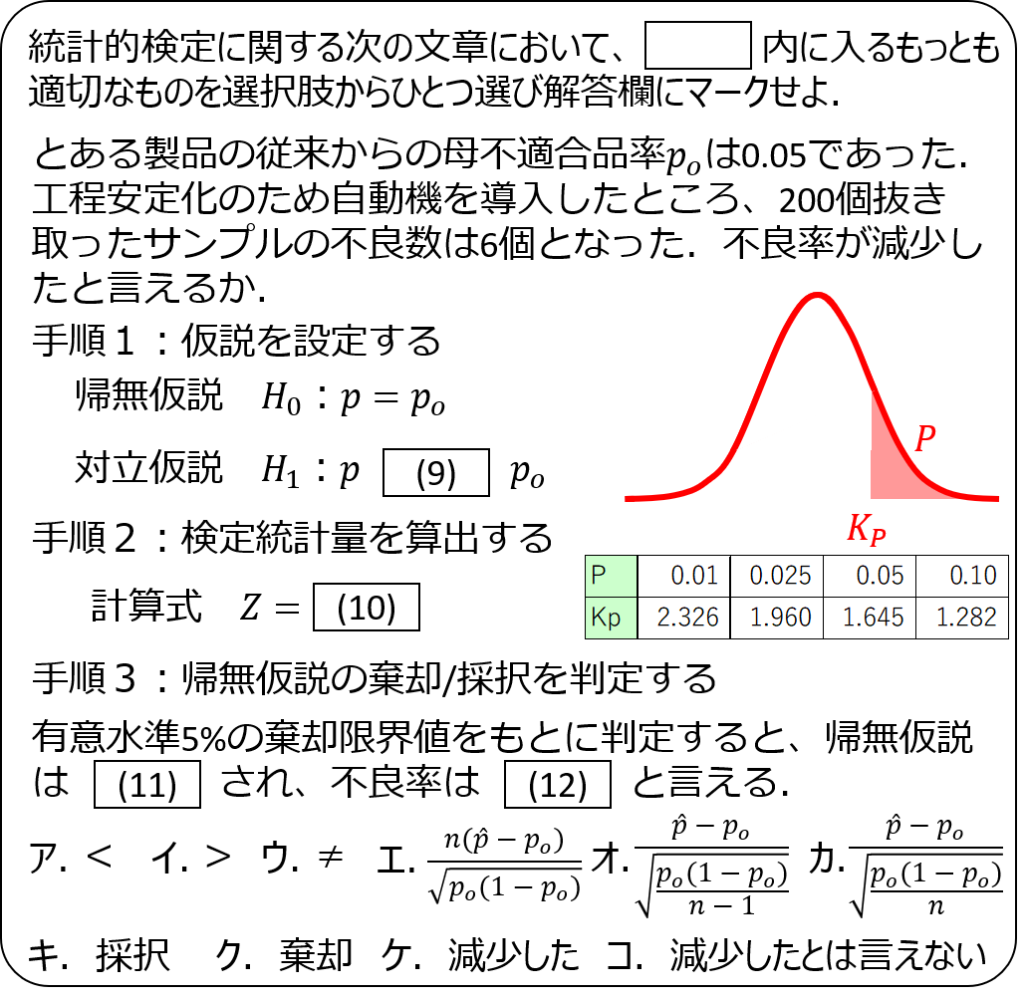
問題4
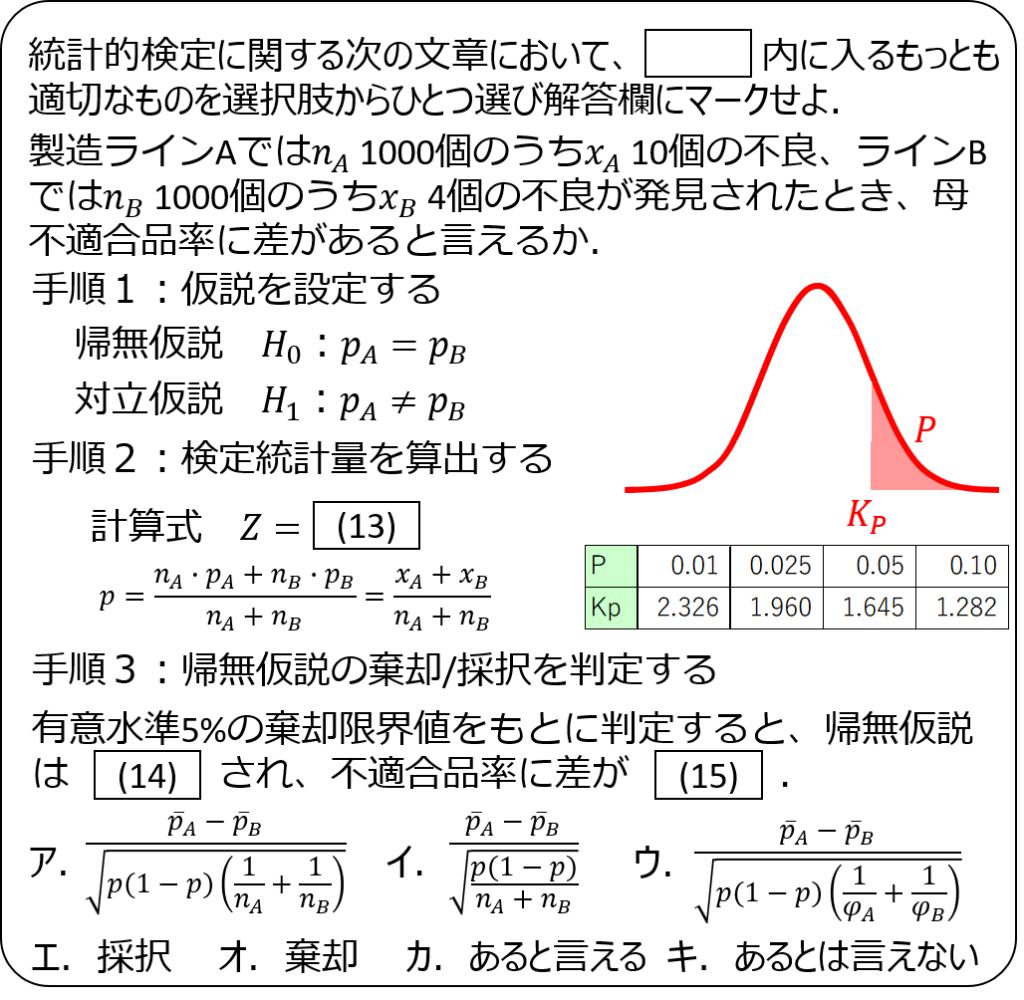
問題5
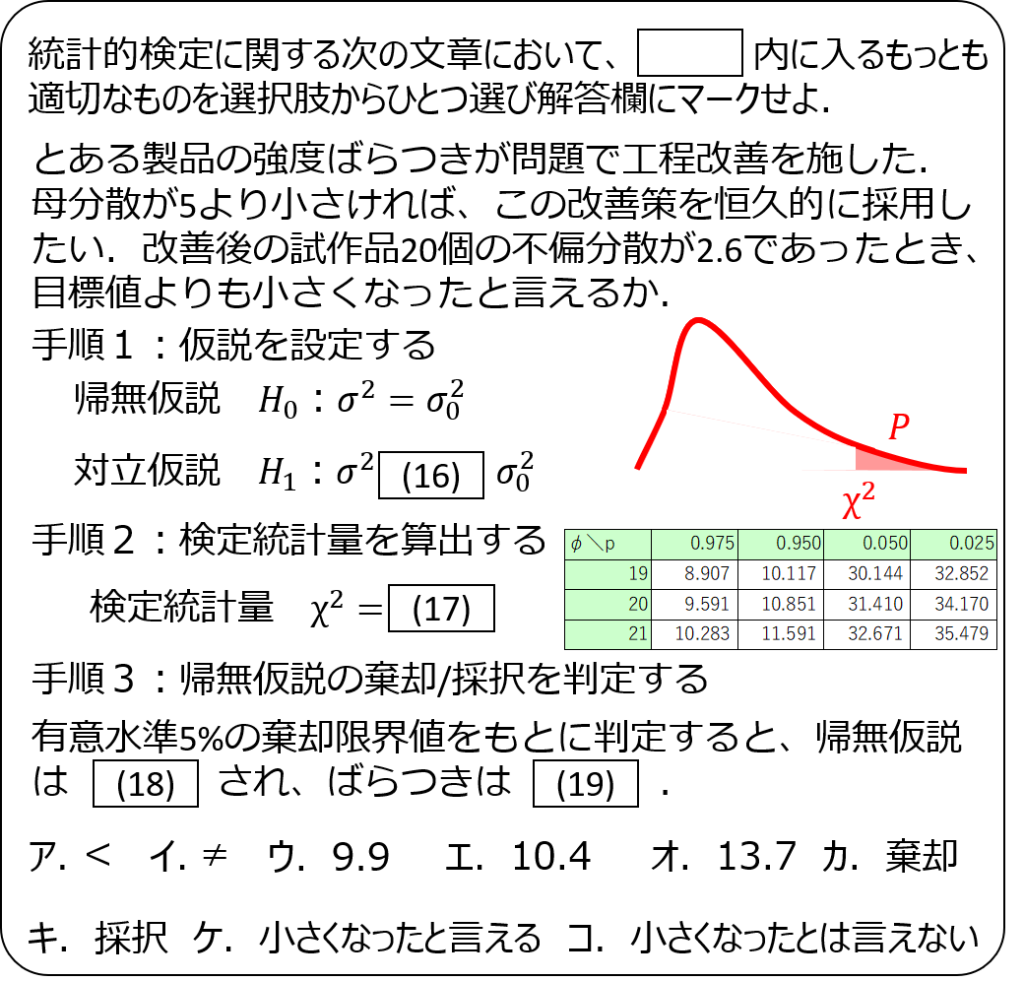
問題6
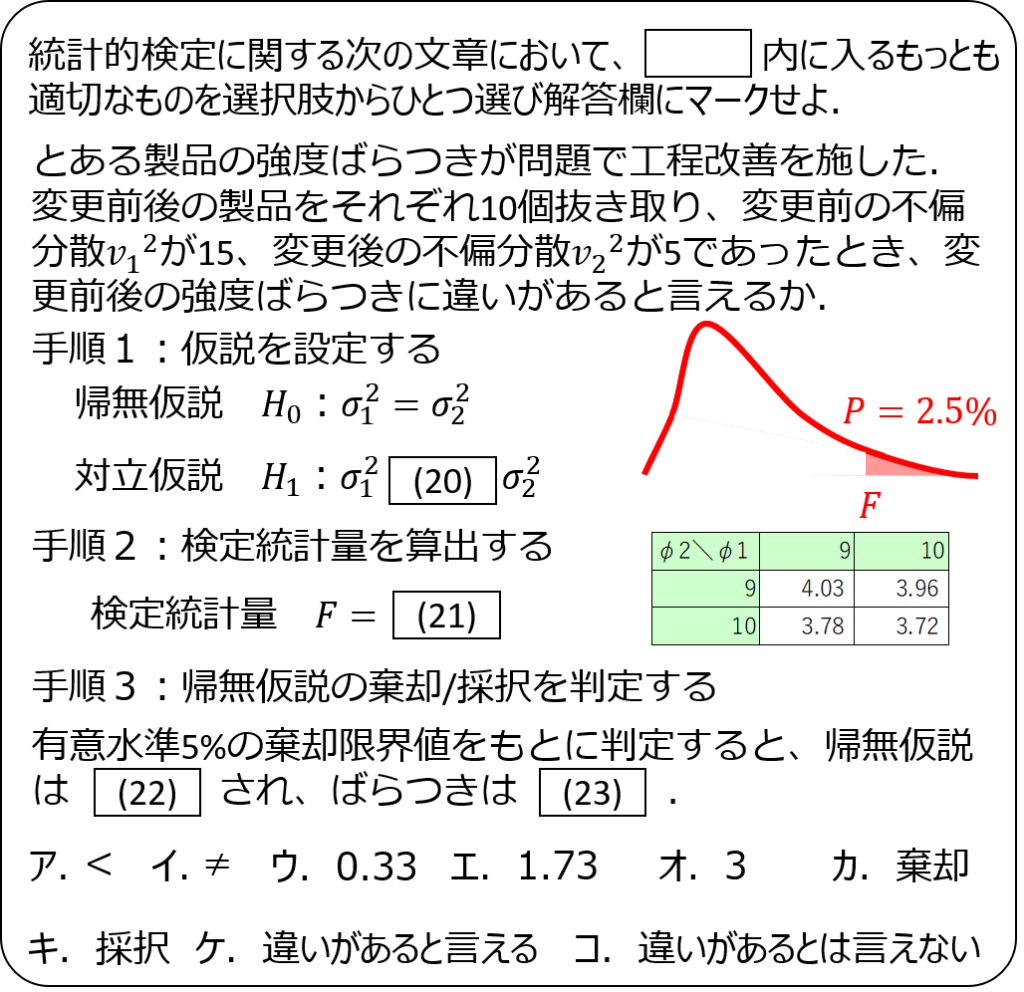
解説1

解説2

解説3

解説4

解説5
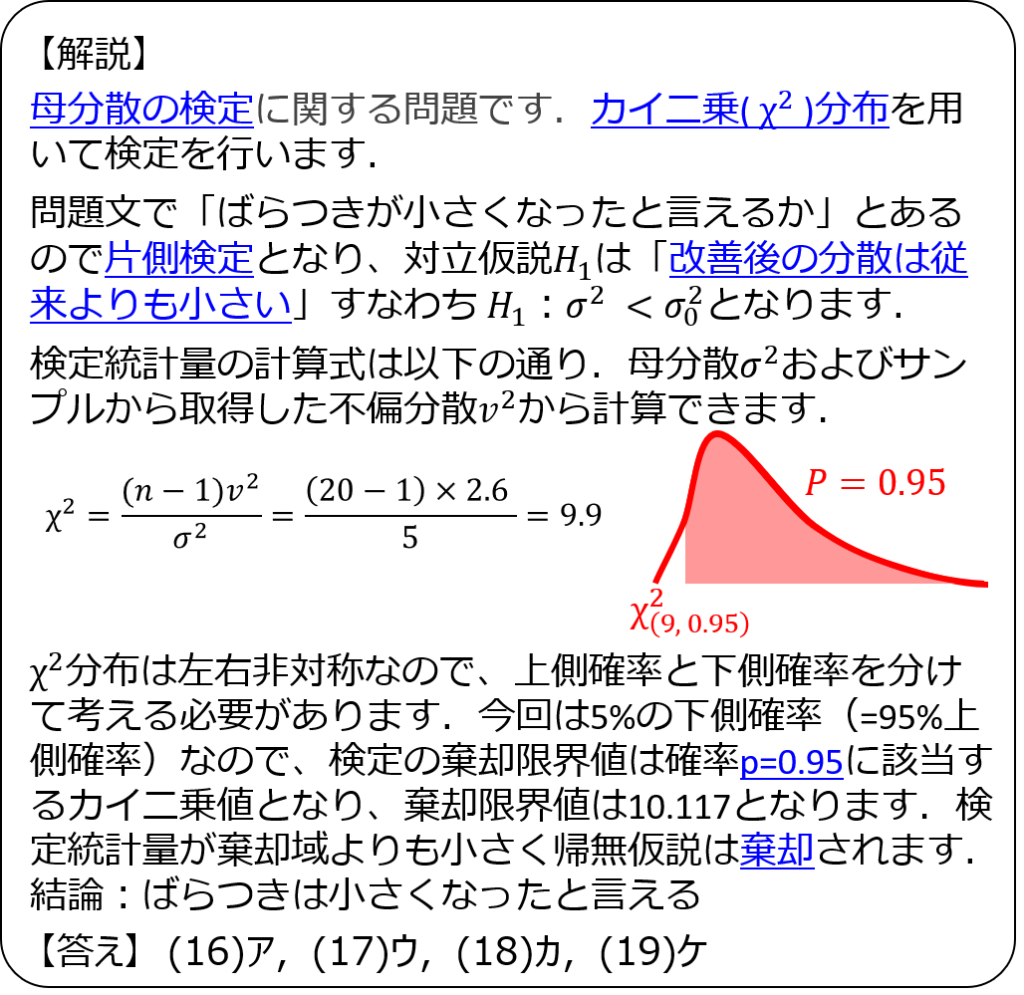
解説6

(補足)F分布の下側確率
実例で示したほうが分かりやすいので、先ほどの問題6を用いて説明します。
2.5%下側確率は式で表すと次のようになります。
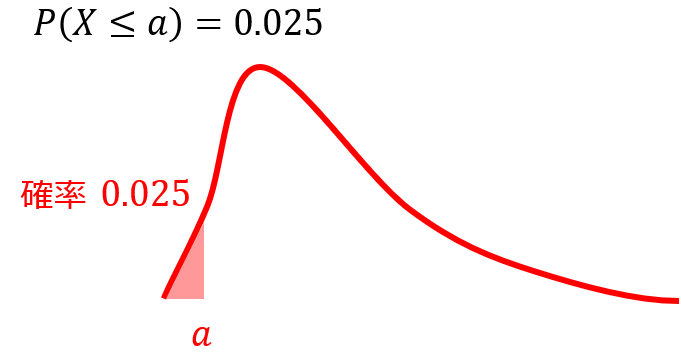
これは、$X$の値が$a$以下となる確率が2.5%となる状態を表しており、まさに分散比の検定で求めたいF値のことを意味しています。
そして先ほどの式のかっこ内を$aX$で割ると以下のようになり、すなわち$1/X$の上側2.5%確率を求める式に変換できるのです。
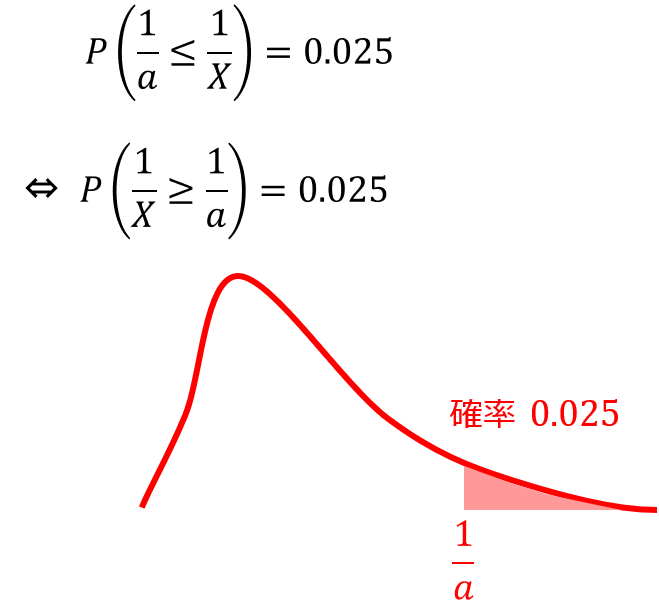
そしてもう一つ、F分布に関する次の性質を利用します。
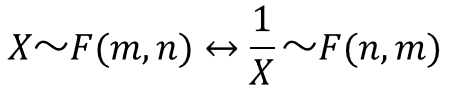
これは、自由度を入れ替えれば逆数のF値を求められるという性質です。
今回の例題では自由度はどちらも9なのでF値は同じであり、単純に逆数を取れば本来の目的である$a$の値が得られます。
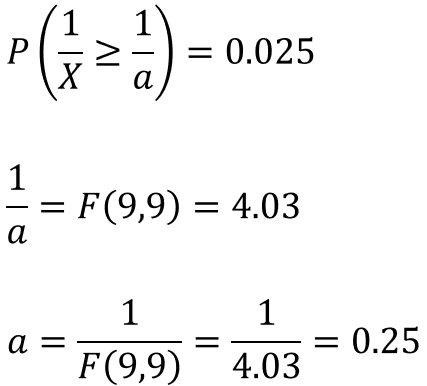
ただ、得られた結果をよく見ると、下側確率の棄却限界値が0.25となっていますが、元々、分散の値の大きい方を分子に設定したので、F値が1未満になるはずがありません。
そのため、当然ながら棄却限界値を下回ることもなく、そもそも下側確率を検定する意味がないのです。
これは、「分散の値の大きい方を分子に設定する」段階で上側確率のみを対象とする前提を与えたことと同義であり、結局のところ上側2.5%点だけで判定が可能なのです。
ちなみに、分母分子の大小の前提を与えなければ、逆数の方が1を超える場合もあるので、上側と下側の両方で判定する必要が生じます。
統計的推定や統計的検定の基本から学び直したいかたに向けては、以下の記事で詳しく解説しています。


なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。




コメント
本日の試験に向けて繰り返し参考にさせていただき大変助かりました。
統計的検定の模擬試験の下記回答が誤記と思われるのでお知らせします。
・Q5の(19)の回答がキ ⇒ケ
・Q6の(21)の回答がエ ⇒オ
解説の中には丁寧に記載があったので誤解は少ないと思いますが、試験前に繰り返し使わせていただいて回答だけ確認するような使い方をしていたので、今後同様の使い方をする場合には直していただけるとありがたいです。
57歳にして3ケ月前に試験を申し込みしてから試験範囲を確認してその広さに圧倒されていました。短期記憶も衰えているのでこのサイトには非常に助けていただきました。