QC検定2級の受検をお考えの皆さま、試験対策は順調に進んでいますか?
この記事では、2級の中でも頻出の実験計画法について、過去問の出題傾向と押さえておきたいポイントを紹介しています。
さらに、模擬問題と解説を合わせて掲載していますので、ぜひ参考になればうれしいです。
また、Youtubeチャンネルでは、実験計画法の基礎知識について詳しく解説しています。
【講義解説】編では全4回の動画で基礎知識を紹介していますので、いきなり過去問や模擬問題を解くのに不安のあるかたは、ぜひご覧ください。
また、【傾向と対策】編では、QC2級の試験を攻略するコツを紹介していますので、こちらもぜひご覧ください。
過去問の出題傾向
実験計画法は、QC検定2級の試験問題で最頻出分野のひとつです。
2018年から2021年までの6回の試験のうち、なんと全ての回で登場しています。
実験計画法はQC検定3級では出題されないので、まさに2級を象徴する分野と言えますね。
裏を返せば、2級の試験対策で初めて登場して、見慣れない計算式や分散分析表に苦手意識を持っているかたも少なくないかもしれません。
しかし、問題の構成と解法は概ね傾向が決まっているので、パターンさえ覚えてしまえば心配する必要はありません。
問題の内容としては、大きく以下に分かれます。
- 分散分析表を計算して埋める問題
- 因子の最適組合せを選び、母平均の点推定を求める問題
- 有効反復数と信頼区間を求める問題
- 実験計画法の定義に関する用語を選ぶ問題
押さえておきたいポイント3選
その1:平方和の計算でつまづくと命取り
実験計画法の問題では、必ずと言っていいほど分散分析表が登場します。
それもそのはず、分散分析で因子の有意性を判定するための手法ですから、その過程の計算方法の理解度を試されるのは当たり前といえます。
分散分析表は基本的に左側の列の(偏差)平方和から計算して埋めていきます。
そのため、最初の平方和を埋める小問で間違えると、当然ながらその後の正答率にも大きく影響してしまいます。
ありがちなミスとしては、行や列の水準の数で割るのを忘れる、修正項を引くのを忘れる、$S_{AB}$を計算して安心してしまい$S_{A×B}$まで求めるのを忘れるなど。
いずれも、私が試験勉強をしていたときに、よくやってしまったミスでした・・・。
そもそも、苦手意識からつい焦ってしまい、問題に着手する段階ですでに浮足立っている可能性もあります。
ただ、よく過去問を分析すると、先ほど紹介したように問題の傾向はほぼ決まっており、慣れてきたら機械的に電卓を叩いて計算をするのみです。
また、実験計画法では問題の中にデータの表が掲載されることが多いので、問題用紙の領域自体が広くとられがちです。
表の中には、データの他に総和、二乗和、平均などいくつかの統計量が記載あり、情報量の多さに圧倒されてしまいそうですが、その中でも計算に使う値は限られているのです。
データから二乗和を懸命に計算していたら、横の方に実は二乗和が記載されていた、なんて場合もあるので、まずは全体を俯瞰して必要な情報を見つけ出すようにしましょう。
その2:電卓のメモリー機能をフル活用
QC検定では試験に電卓を使うことが許可(関数電卓など除く)されていますが、実験計画法は電卓を最も活用する分野と言っても過言ではありません。
親切に問題文中に二乗和がすべて記載されていれば良いですが、そのケースの方が稀であり、特に交互作用の偏差平方和はデータから二乗和を自分で計算することが多いです。
そのため、各データの二乗の計算結果をいちいちメモして後で合算するような非効率なことをせずに、電卓を叩く回数自体を減らすことが求められます。
具体的には電卓のメモリー機能を使えば、各データの二乗の値を電卓のメモリー上に加算していって、最後に累積値を呼び出すことができます。
メモリーキーの機能は以下の通り。
- 「M+」メモリープラス:表示されている数値をメモリーに足す
- 「M-」メモリーマイナス:表示されている数値をメモリーから引く
- 「MRまたはRM」リターンメモリー:メモリーの数値を呼び出す
- 「MCまたはCM」クリアメモリー:メモリーの情報を消去する
- 「MRC」:1回押すと「MR」、2回押すと「MC」の機能
例えば、以下のように平方和を計算できます。

なんと、こんな複雑な計算でも一度に計算できてしまうんですね。
これなら途中で二乗の値をメモする必要がなくて、さらには書き取りや打ち込みのミスも減らすことができ、時間短縮とケアレスミス削減の両方に効果的です。
私自身もいままでほとんど使ったことのない機能でしたが、QC検定をきっかけに覚えて、実際に試験でもフル活用しました。
ちなみに、メモリーが残った状態は電卓の数値の左上の方に[M]という表示が出ます。
うっかり、前のメモリーが残ったままにならないよう、計算が終わったら[MC]クリアメモリーで消去することを忘れないようにしましょう。
その3:区間推定は余力があれば解く
後ほどの模擬問題でも紹介しますが、分散分析の続きとして最適水準の点推定の信頼区間(区間推定)を求める問題が最後の方に出題されることがあります。
点推定の平均値を求めるところまでは考え方も分かりやすく、しっかりと得点できるよう押さえておきたいところです。
しかし、区間推定まで踏み込むと、突如として有効反復数という全く聞きなれない用語が登場し、謎の分数が選択肢に入ってくることがあります。
実際の計算自体は四則演算で対処できるのでそれほど構える必要はないのですが、個人的にはここまで無事に到達したら思い切って飛ばしても良いのではないかと思っています。
というのも、有効反復数は田口の式や伊奈の式の2通りの求め方があり、自由度と水準の数、分母と分子がごちゃ混ぜになって、私の経験談として暗記にかなり苦労したからです。
さらには、参考書や問題集によってどちらを使うかまちまちであったりするので、なかなか使いこなせるレベルに到達するのがむずかしいと思います。
QC検定では満点を求められているわけではなく、あくまでも合格基準の目安は正答率7割程度です。
そのため、一つの小問を取るために多大な時間を費やして、他の問題を解く時間がなくなってしまっては元も子もありません。
区間推定は一番最後の設問で登場する傾向が多く、後ろの小問への影響はほとんどないので、最後に時間が余ったら解くくらいの心の余裕があっても良いかと思います。
そもそも、有効反復数を即答できるくらいの知識レベルをお持ちであれば、QC2級は余裕で通過できそうな気がしますからね。
もちろん、実験計画法を得点源とされている方はご自身にあった戦略があると思いますので、選択肢の一つとしてご紹介したまででした。
模擬問題
実験計画法に関する練習問題を5つ用意しました。
QC検定2級の出題分野としては、一元配置実験、繰り返しのない二元配置実験、繰り返しのある二元配置実験といったように、いくつかの種類があります。
ただ、繰り返しのある二元配置実験が最も理解度を求められるので、ここを中心とした模擬問題にしています。
実際に過去問でも繰り返しのある二元配置実験が多く出題される傾向にあり、避けては通れない学習分野と言えるので、ぜひマスターしておきたいところです。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題1
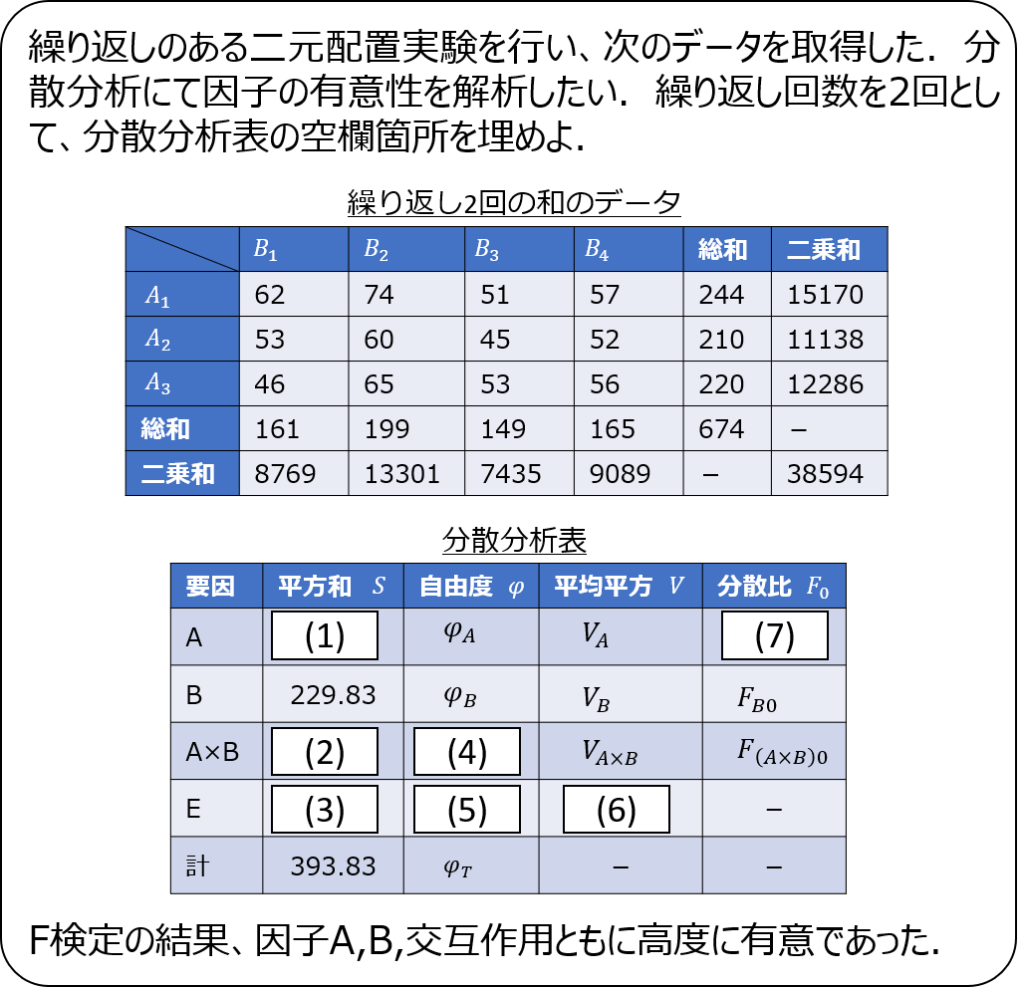
問題2
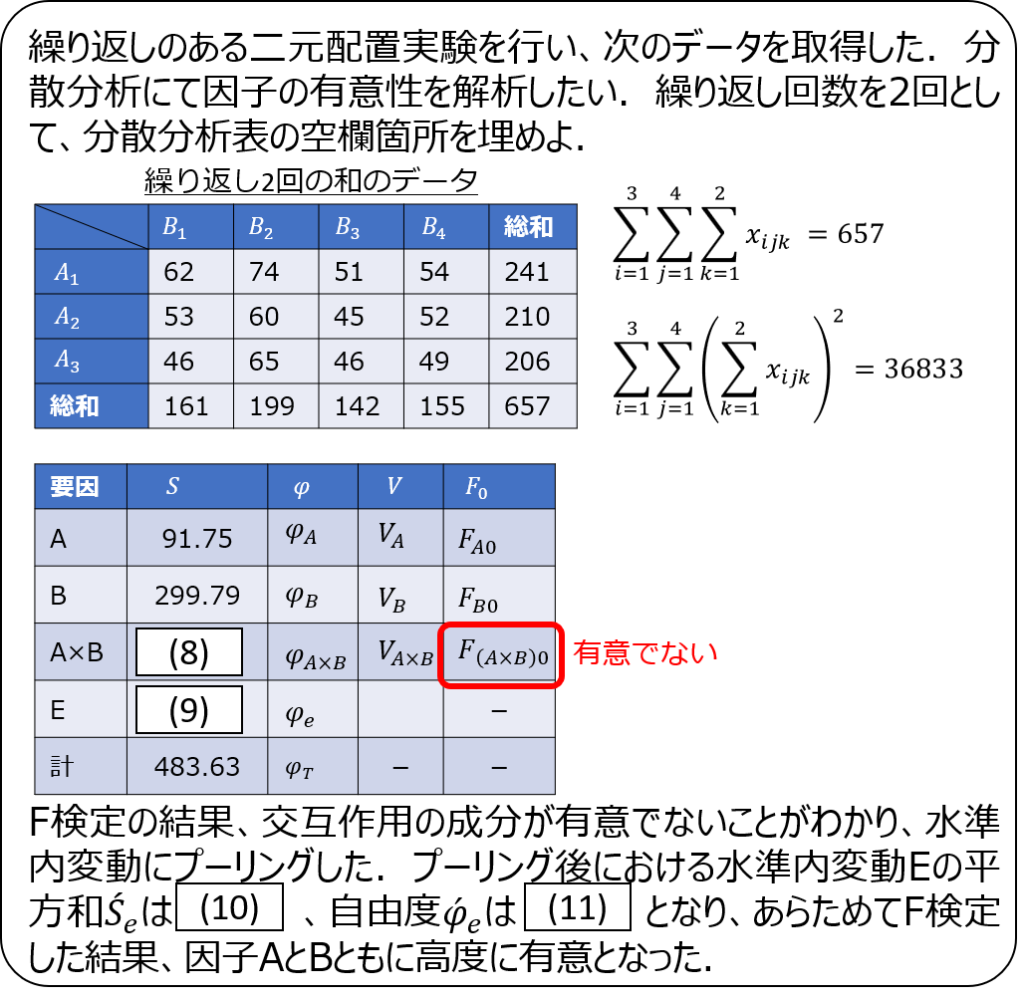
問題3
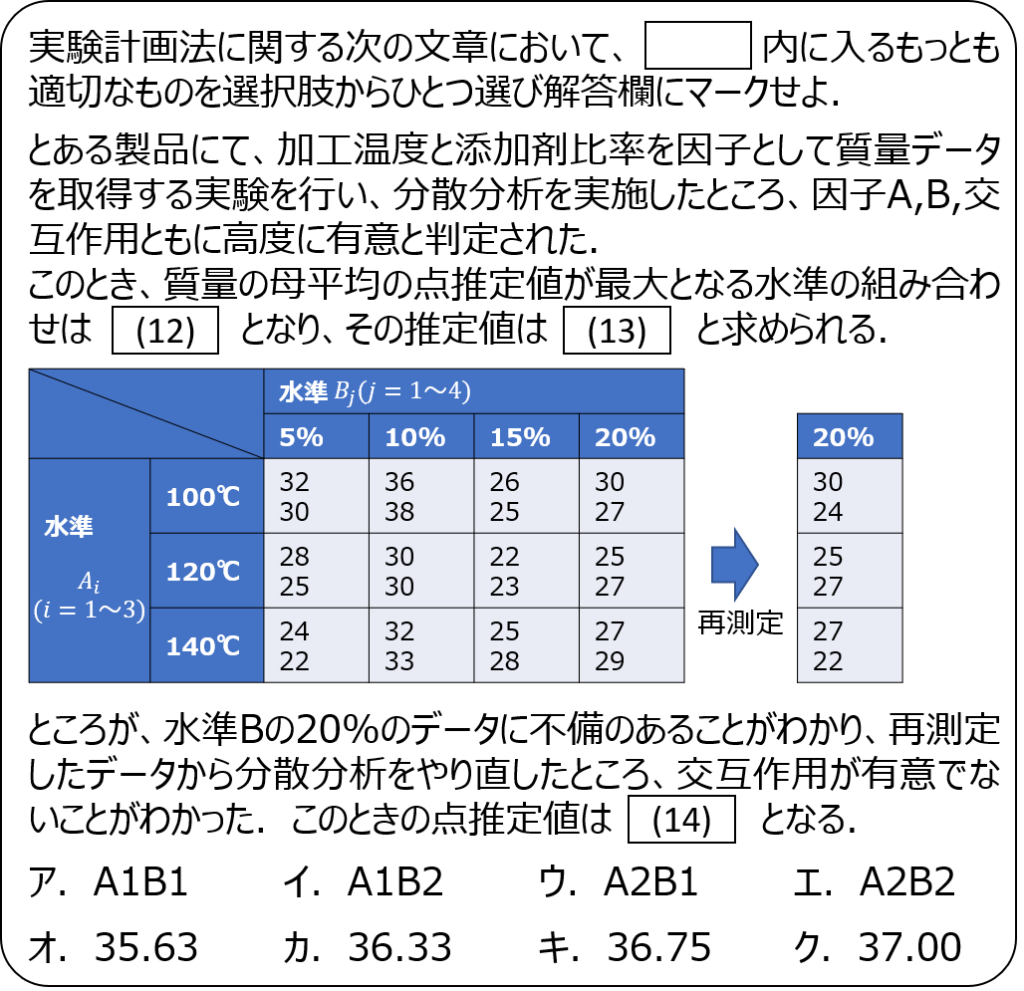
問題4
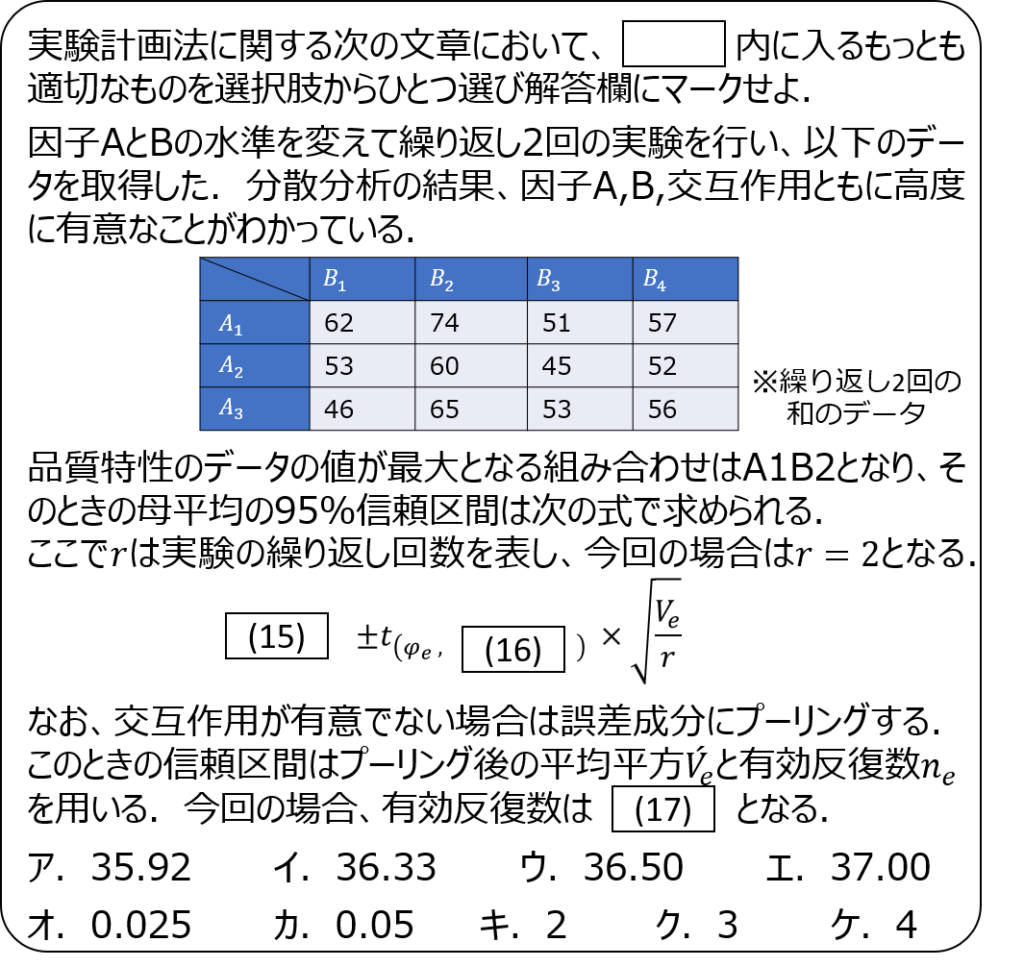
問題5

解説1
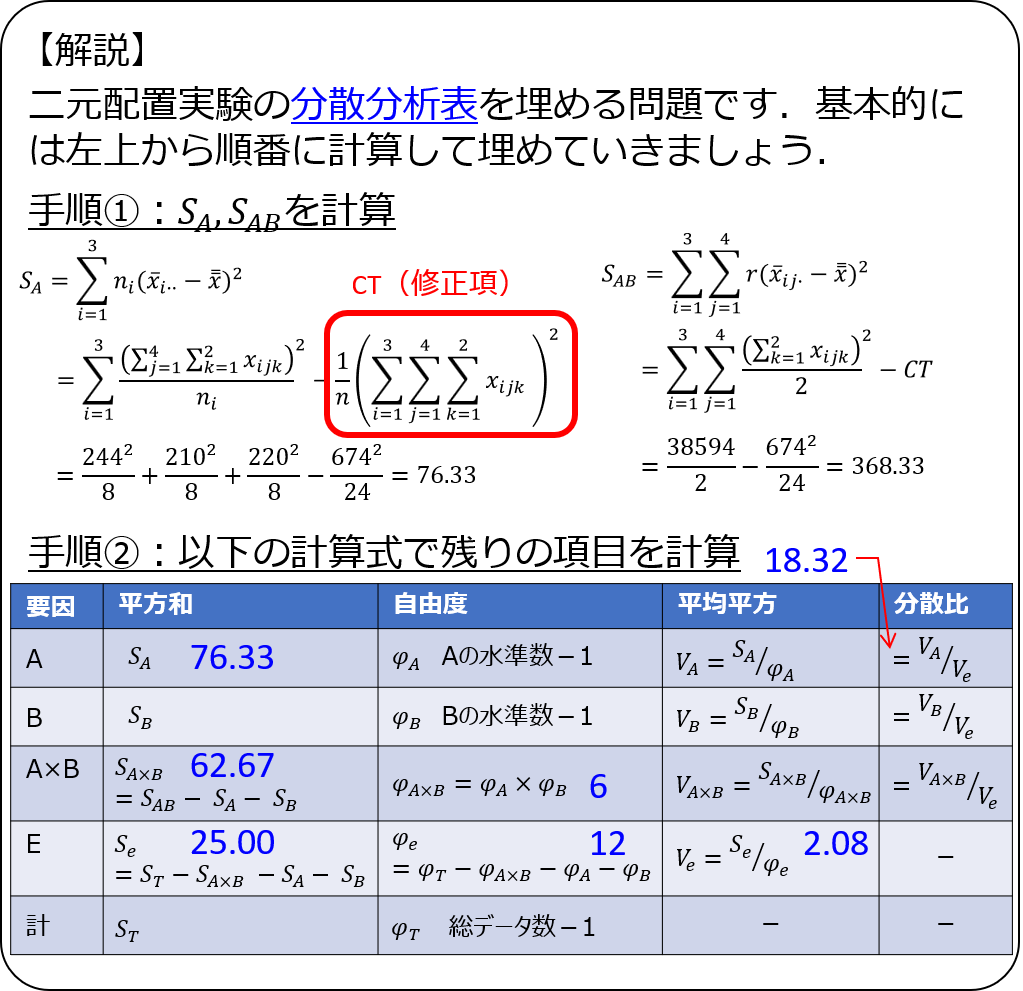
解説2

解説3
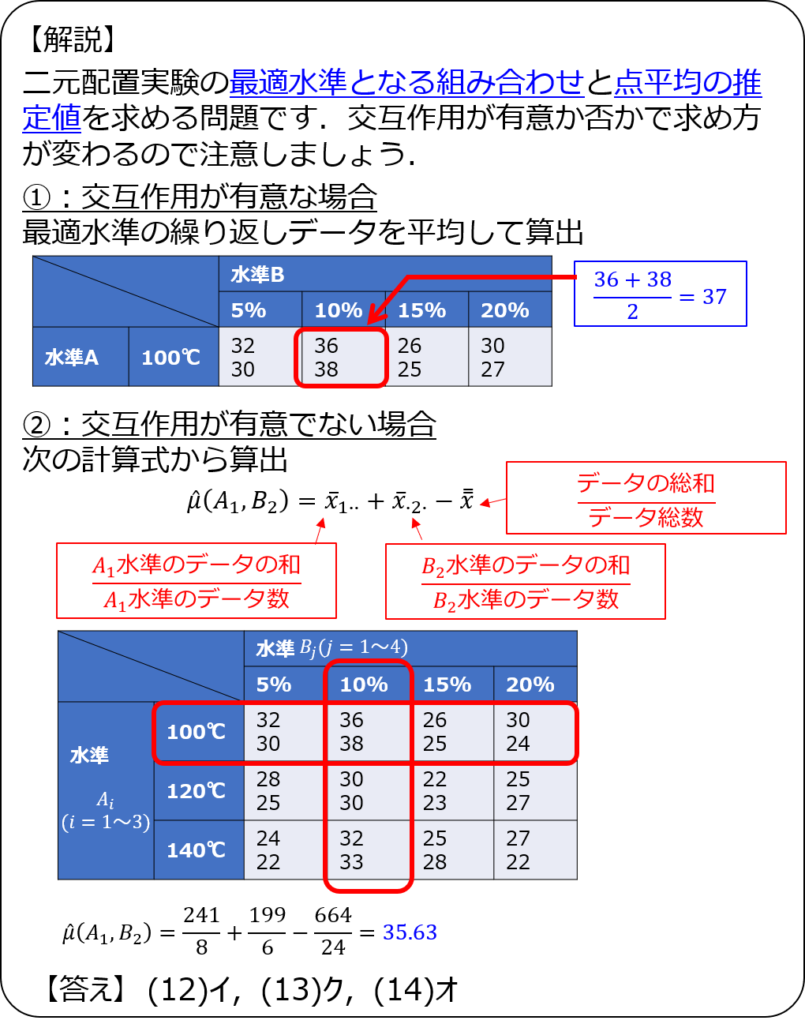
解説4

解説5

実験計画法の基本から学び直したいかたに向けては、以下の記事で詳しく解説しています。

また、繰り返しのある二元配置実験に特化した記事もありますので、合わせてご覧ください。


なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。




コメント
問題2の総和が間違っています。
表では674となっていますが、正しくは657です。
657で計算すると解説のとおりの答えとなります。
ご指摘ありがとうございます。
総和657が正しいので修正いたしました。