QC検定2級の受検をお考えの皆さま、試験対策は順調に進んでいますか?
この記事では、2級の中でも頻出の確率分布について、過去問の出題傾向と押さえておきたいポイントを紹介しています。
また、模擬問題と解説を合わせて掲載しましたので、ぜひ参考になればうれしいです。
過去問の出題傾向
2018年から2021年までの6回の試験のうち、確率分布は4回で出題される最頻出分野の一つです。
内容としては、大きく以下に分かれます。
- 定義の式や文章に合致する確率分布の名称を選ぶ問題
- 与えられた定義の式を用いて確率を計算する問題
- 平均値と標準偏差を用いて正規分布表の確率を読み取る問題
- 上記の逆算で確率に対応する平均値と標準偏差を求める問題
押さえておきたいポイント3選
その1:式の見た目に圧倒されない
まず、QC2級では正規分布、二項分布、ポアソン分布が出題の対象となっています。
3級ではポアソン分布はなかったので、2級から新たに登場となります。
それぞれの確率分布について、問題文に定義の式が与えられることが多く、ここまでは親切で助かるのですが、この式の形を見て圧倒されてしまいそうになります。
二項分布は$C$や累乗、ポアソン分布は階乗やネイピア数$e$が出てきて、電卓を使ってよいとはいえ、計算するのに気が重いですね。
また、正規分布は聞きなじみもあるので、すんなりと入ってくるかと思いきや、案外と確率密度関数の式は複雑です。
確率関数を一覧で表すと次の通り。

しかし、式の形だけ見て圧倒されて、焦ってはいけません。
例えば、二項分布では途中まで計算がされていたり、正規分布では結局のところ式を使わずに正規分布表だけで答えが導けたり、真っ向から挑む必要のないことも多いです。
そもそも、関数計算機能のない電卓では累乗の計算をまともにできないことも多く、定義の式は対応する確率分布の名称を選ぶためだけに登場している場合もあります。
そのため、問題文を細部まで読めば、案外と簡単な計算だけで対処できるので、落ち着いて解き進めていきましょう。
その2:正規分布と二項分布は3級問題とあまり変わらない
ポアソン分布は2級からの登場ですが、正規分布と二項分布は3級でも出題される分野です。
3級と2級の過去問をご覧になったことのあるかたは、お分かりいただけるかと思いますが、問題の内容は双方であまり変わりません。
例えば正規分布では、平均値と標準偏差を元に正規化(標準化)して正規分布表から対応する確率を求める問題が多いですが、3級でもほぼ同じ解法を使う問題が登場しています。
そのため、過去に3級を受検されてきた方にとっては、あまりハードルを感じない分野かもしれませんね。
その3:ポアソン分布の計算ではネイピア数の値をすべて使うとは限らない
ポアソン分布の確率計算では、ネイピア数$e$を用いた計算が登場します。
「ネイピア数なんて普段から覚えてないよ」というかたもご安心ください。
問題文に値を記載してくれているので、これを用いれば良いです。
ただし、$e$の値だけでなく、$e^{-1}$や$e^{-2}$も合わせて与えられていることが多いのですが、一つ注意点としてこれら全ての値を使う必要はないということです。
登場する数値はすべて用いないといけない気がしますが、そんなことはありません。
むしろ、$λ$の値が変わらなければ累乗の値も一つしか用いる必要はないので、余計に足すような無用な深読みはしないようにしましょう。
模擬問題
確率分布に関する練習問題を5つ用意しました。
このうち、正規分布と二項分布については、2級と3級で出題内容がおおむね同じなので、3級対策で紹介した問題と同じものを用いています。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題1
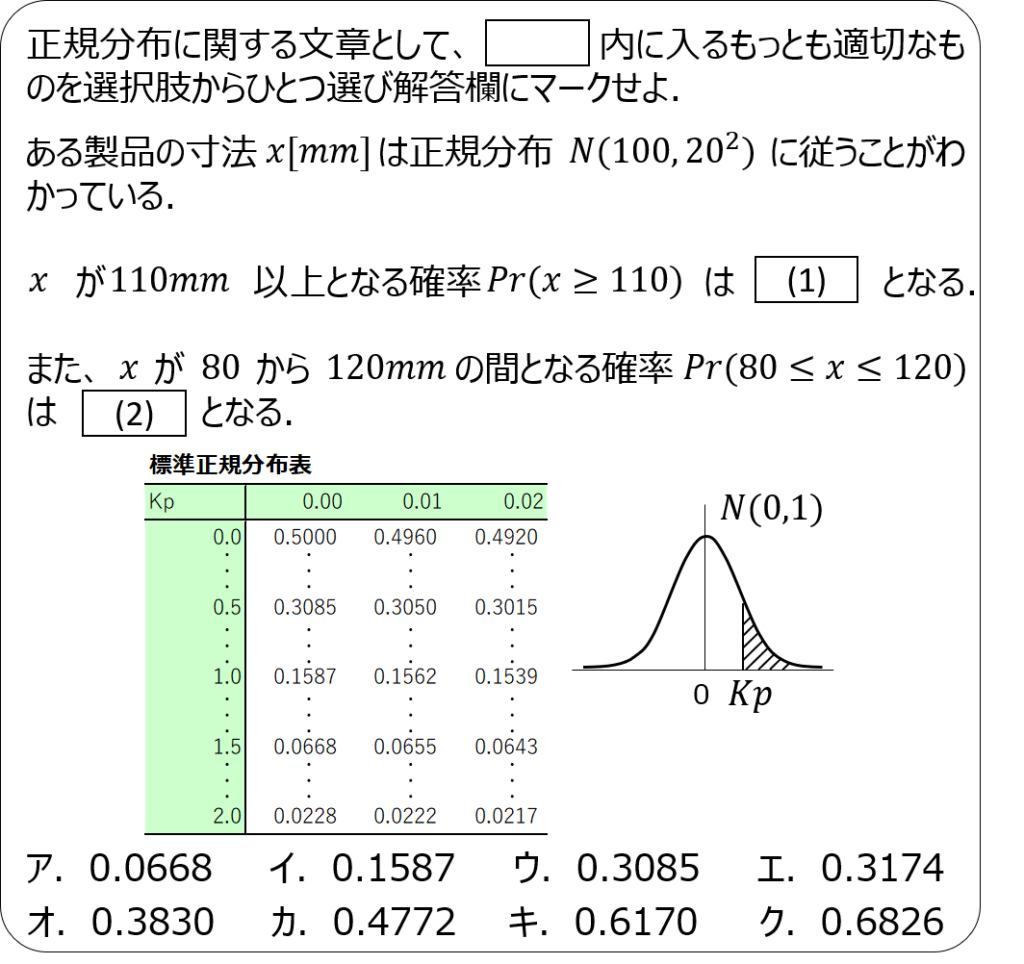
問題2
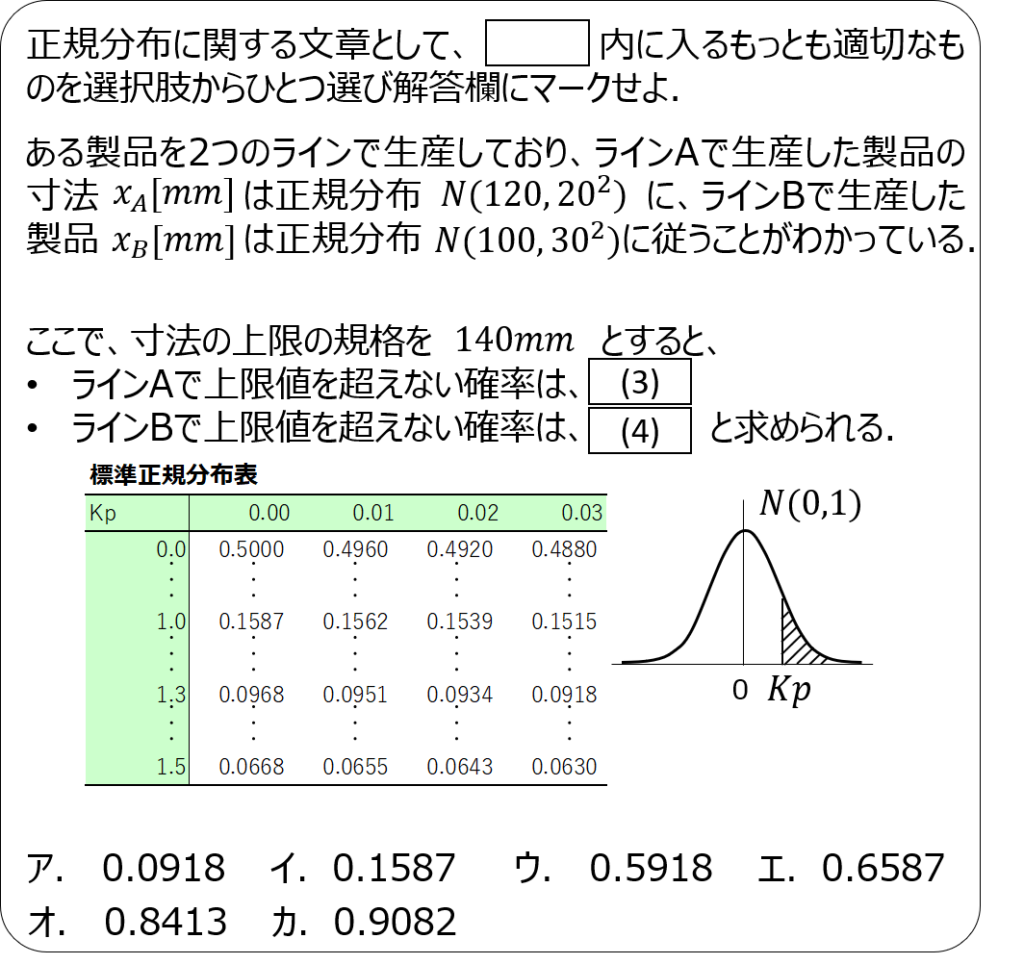
問題3

問題4
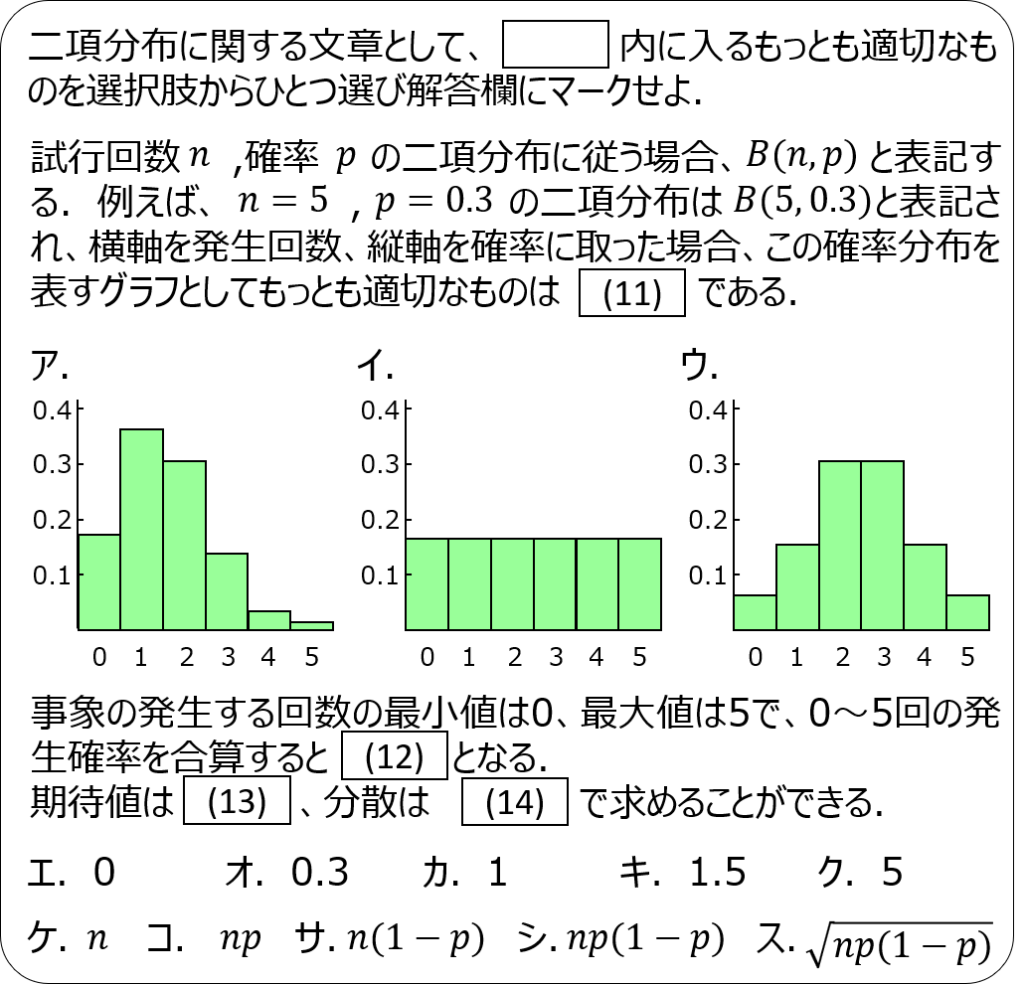
問題5

解説1
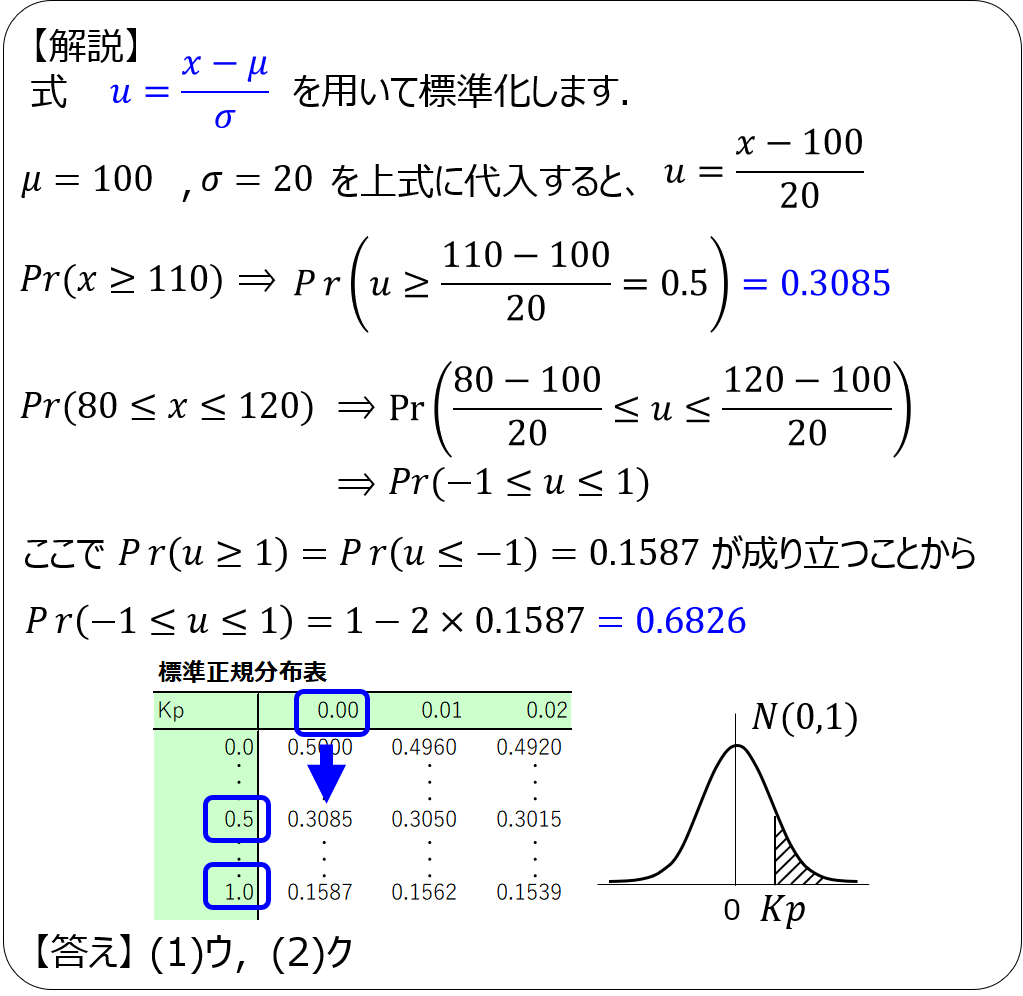
解説2
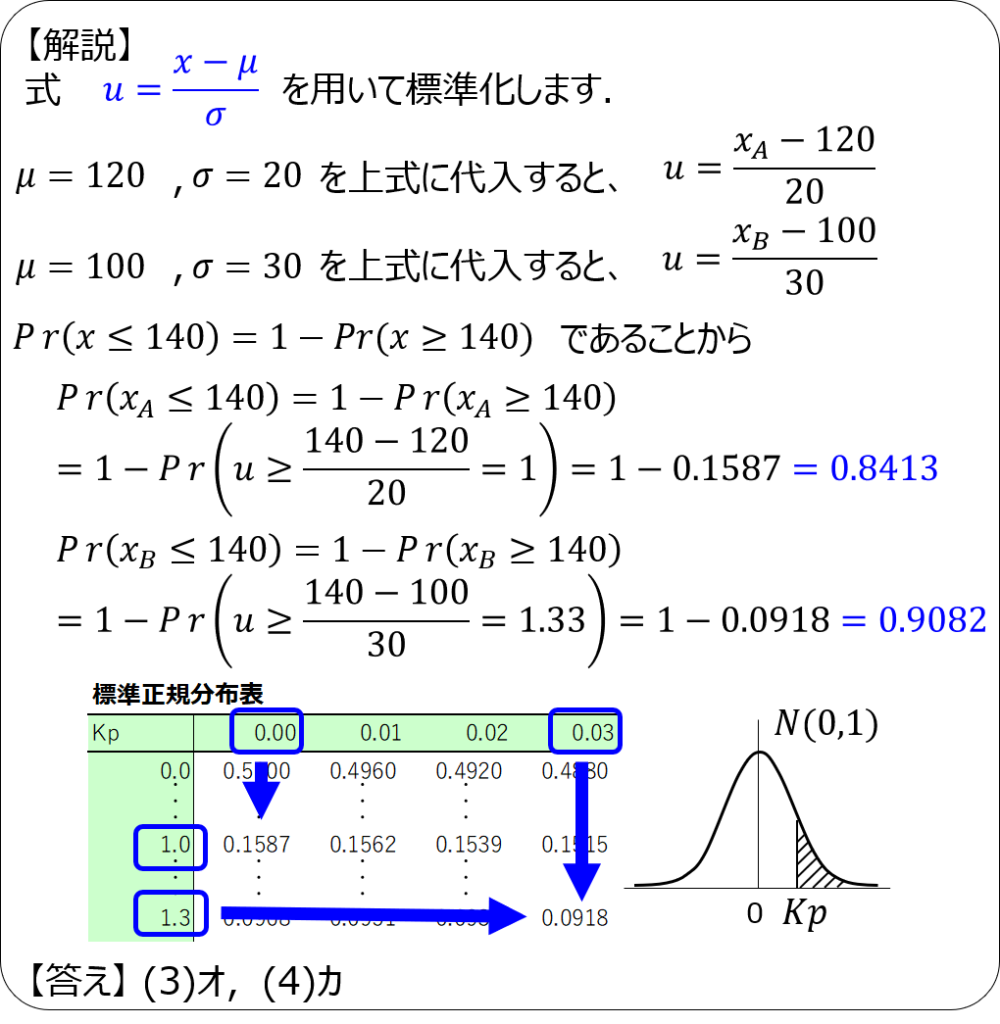
解説3

解説4

解説5

確率分布の基本から学び直したいかたに向けては、以下の記事で詳しく解説しています。




なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。




コメント