QC検定3級の受検をお考えの皆さま、試験対策は順調に進んでいますか?
この記事では、正規分布・二項分布に関して、過去問の出題傾向、押さえておきたいポイントを紹介しています。
さらに、模擬問題と解説も合わせて掲載していますので、ぜひ参考になればうれしいです。
また、Youtubeチャンネルでは模擬問題の解説に加えて、正規分布・二項分布の基礎知識についても動画で解説していますので、あわせてご覧いただけると幸いです。
過去問の出題傾向
正規分布・二項分布は、QC検定3級の試験問題で頻出の分野のひとつです。
2018年から2021年までの6回の試験のうち、正規分布は計4回で登場しています。
また、二項分布は1回しか登場していませんが、何も予備知識のない状態で試験に挑むと全く歯が立ちません。
覚える項目はたいして多くないので、どの分野が出ても対応できるように準備しておきましょう。
問題の内容としては、大きく以下に分かれます。
- ある範囲に入る確率を求める問題(正規分布)
- 標準化の定義の式を問う問題(正規分布)
- 工程能力指数と関連させた問題(正規分布)
- 定義に関する問題(二項分布)
- 説明文に対応する図を選ぶ問題(二項分布)
押さえておきたいポイント3選
その1:標準正規分布表の読み取りは必須
正規分布の問題を解くにあたって、標準正規分布表を読み取るのは必須のスキルです。
QC検定3級では、付表として標準正規分布表が問題用紙の末尾に掲載されており、以下のような様式でマトリックス状に値が割り振られています。
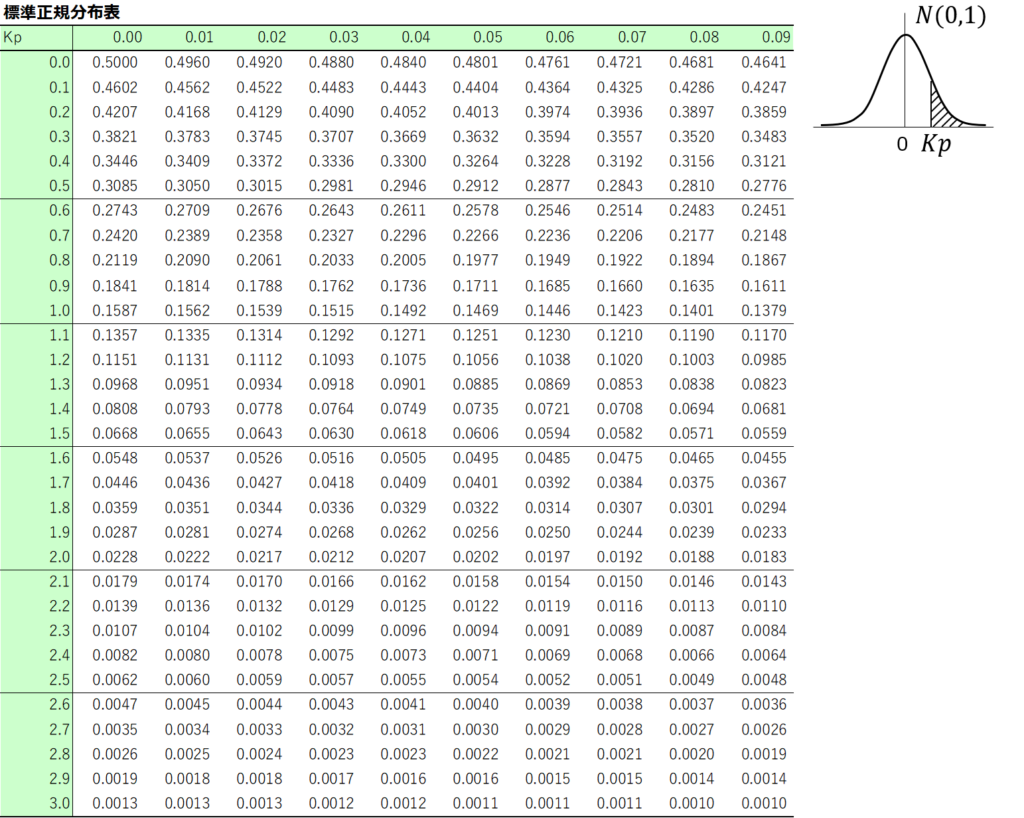
これを用いて、該当するKp値(元データを標準化した値)に対応するP(確率)を読み取らなければなりません。
しかし、行と列が何を意味するのか、Pはどの部分の確率を示しているのか、分布の左半分はどうやって求めるのか、初見では悩んでしまうかもしれません。
ですが、一度理解してしまえば読み取る手順はとても簡単で、複雑な計算も不要ですので、ご心配なく。
Kpは縦軸に示す値が小数第一位まで、横軸の値が小数第二位を表しており、これらの交差する箇所に記載された値が、縦軸と横軸の値を合算したKpに対応する確率Pとなります。
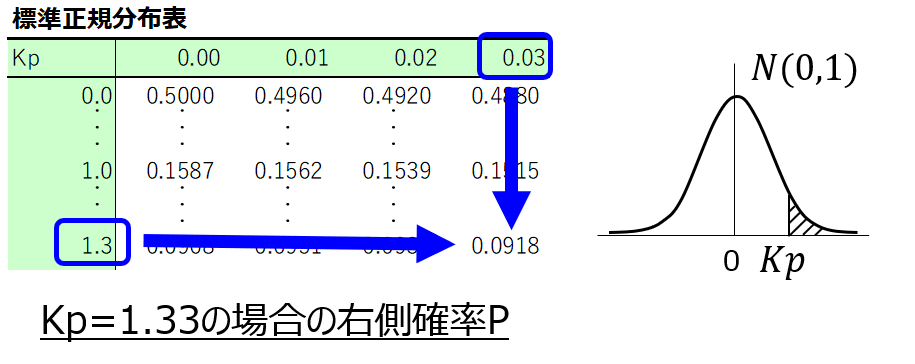
また、標準正規分布表の脇に分布のグラフイメージが示されており、斜線部で示す範囲が確率Pに当たります。
つまり、標準正規分布表で記載された確率Pは、Kp値がその値以上になる確率(右側確率、または上側確率)を表しているのです。
その2:右側確率なのか左側確率なのか
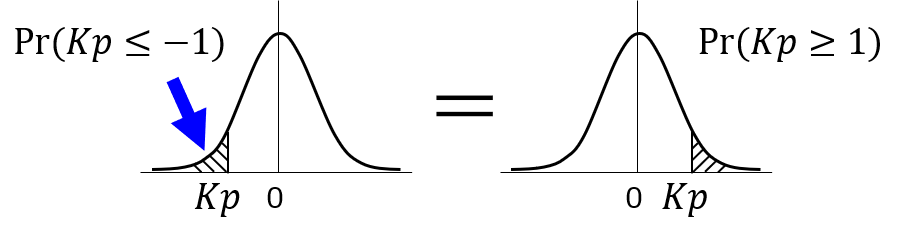
標準正規分布表のもう一つの注意事項として、Kpが0より小さい値の確率は記載されていない点です。
それもそのはず、正規分布では左右対称となるため、左側確率を示す必要がありません。
例えば、Kp≤-1に該当する確率(左側確率、または下側確率)を求めたい場合には、右側確率と同じなので、Kp≥1に置き換えられます。
また、-0.5≤Kp≤1の範囲を求めたい場合には、以下のように置き換えて求めることができます。
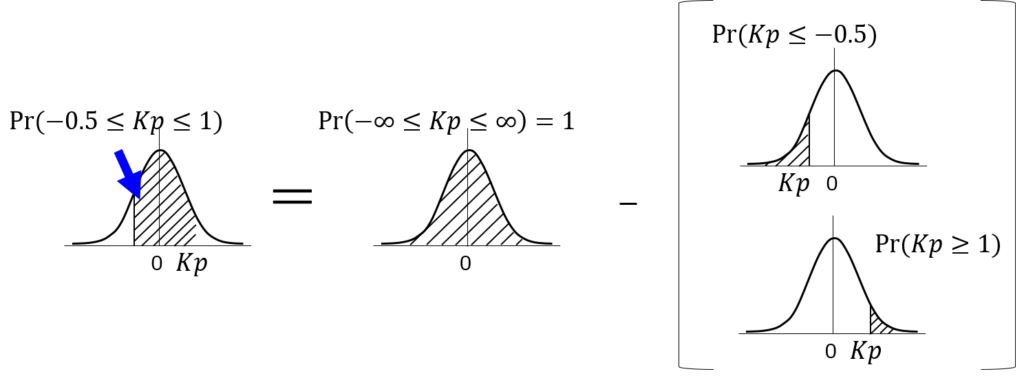
このように、右半分の確率が分かっていれば、任意の範囲の確率を計算することができるのです。
その3:二項分布は定義、期待値、分散の式を覚える
二項分布の出題頻度はそれほど高くないですが、定義の式も複雑で、期待値や分散を自力で導き出すのは非常に困難なので、諦めて基本の式だけ覚えてしまいましょう。

定義の式は高校数学で見たことのある方も多いかもしれませんが、その事象が起きる回数と起きない回数をそれぞれ累乗し、その通り数を掛けて確率を求めます。
何となく意味を理解しておけば、定義の式を覚えるのも困難ではありません。
また、期待値$np$は回数と確率を単純にかけただけのシンプルな計算式なので、これも覚えるのは難しくないでしょう。
分散は式が少し複雑ですが、ここまで答えられたら二項分布の問題はほとんど網羅できるといっても過言ではないので、頑張ってあと一息頭に詰め込んでしまいましょう。
模擬問題
正規分布・二項分布に関する練習問題を4つ用意しました。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題1
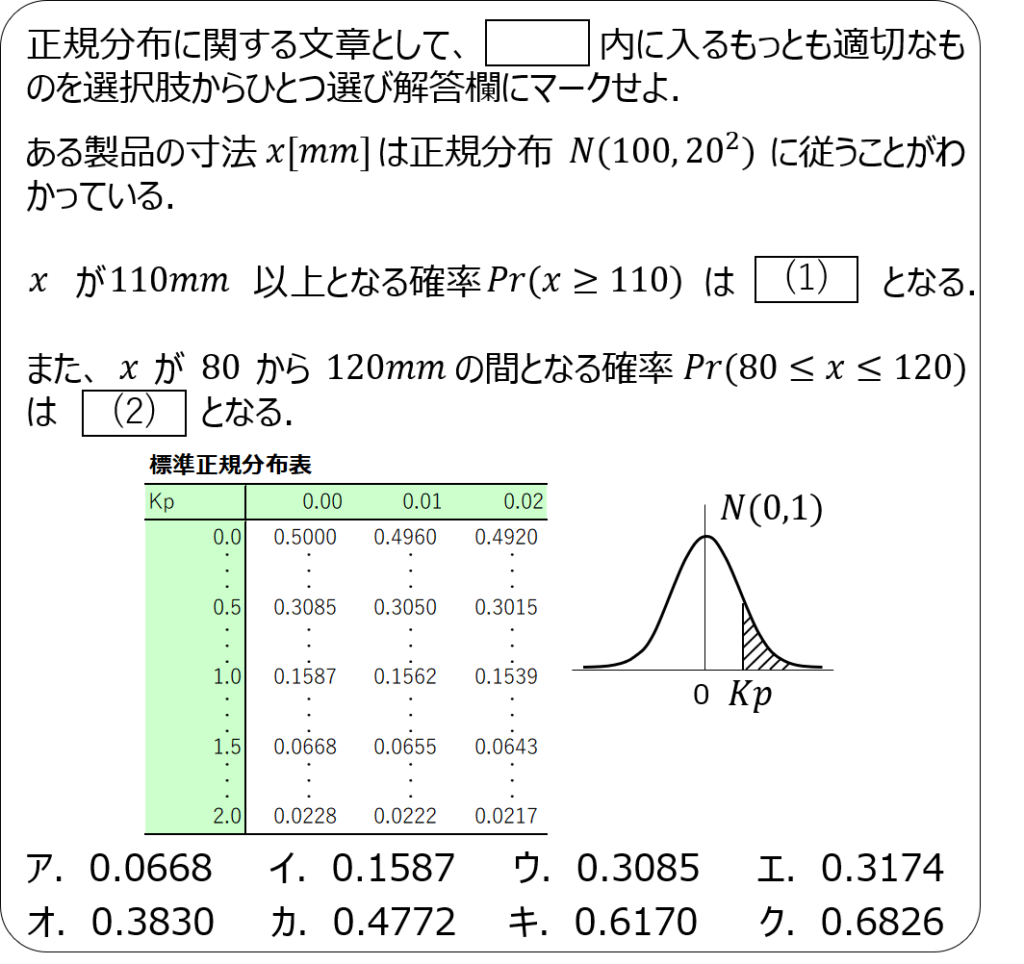
問題2
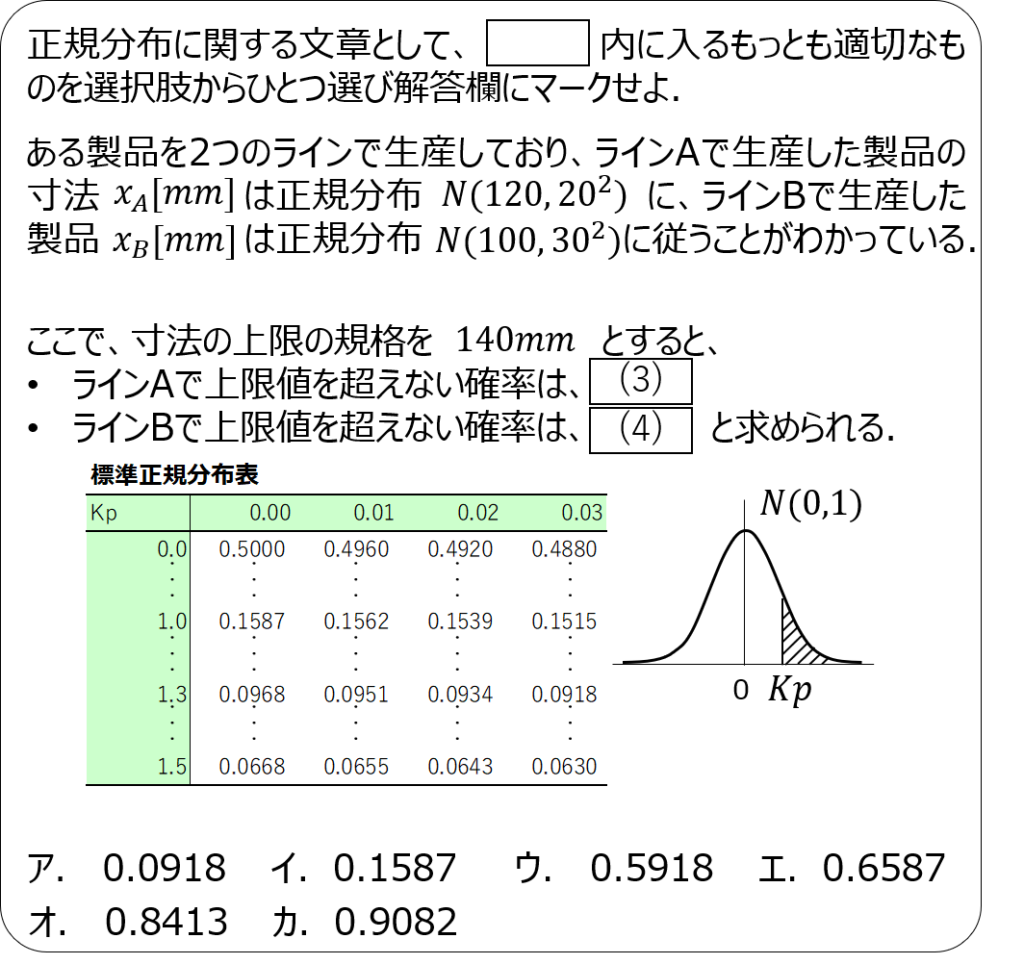
問題3

問題4
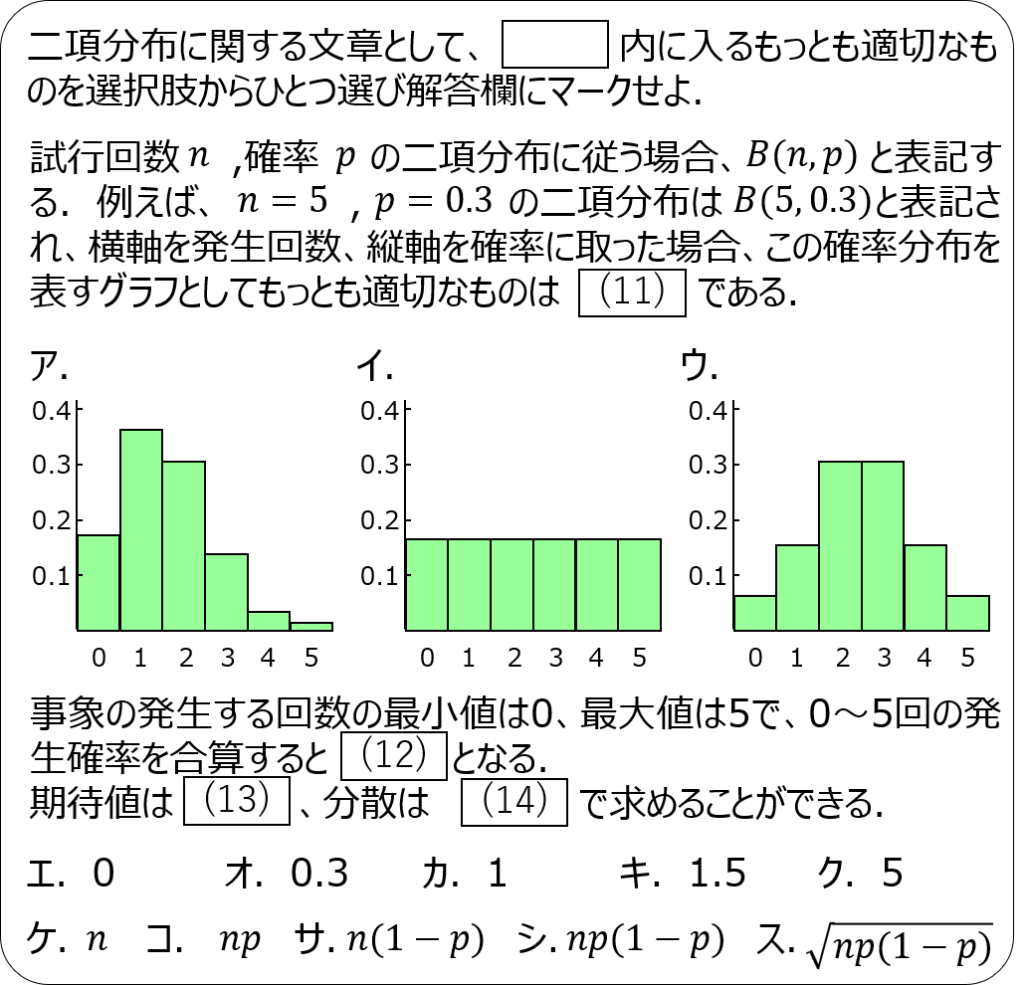
解説1
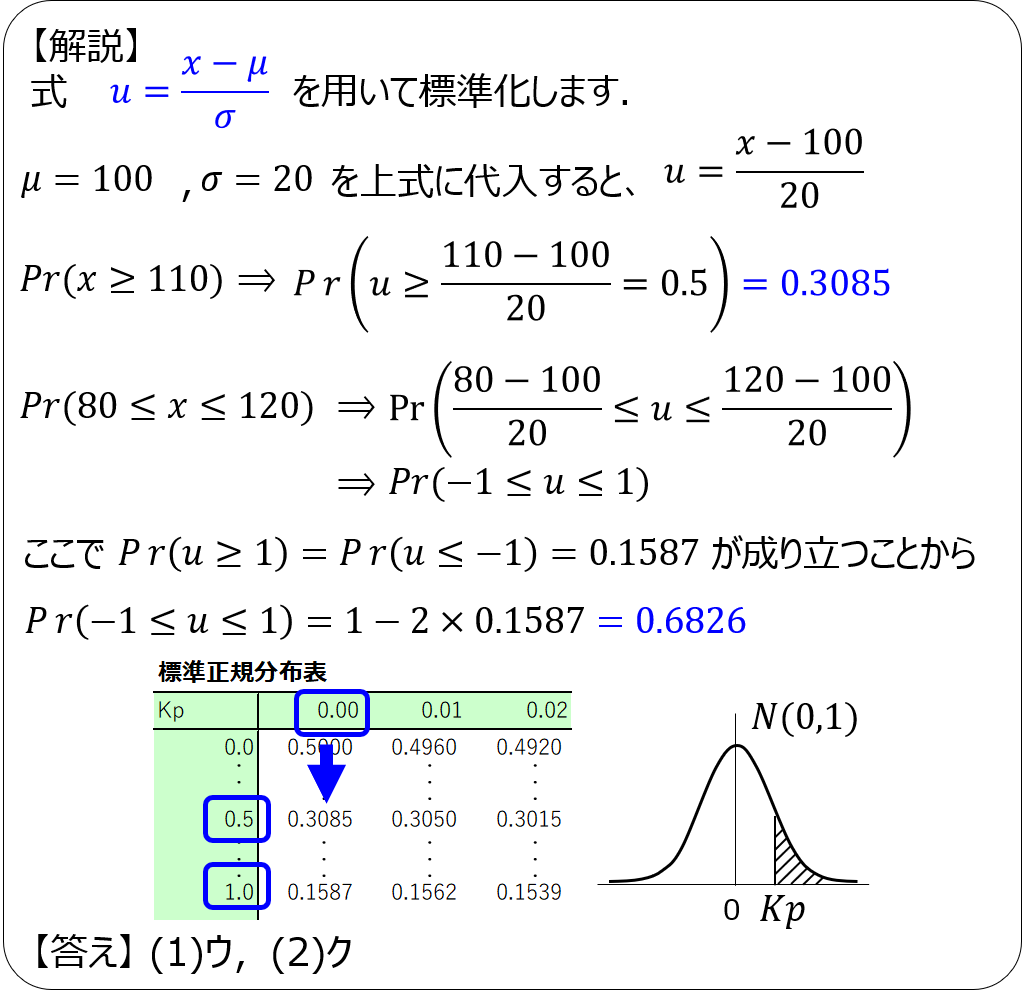
解説2
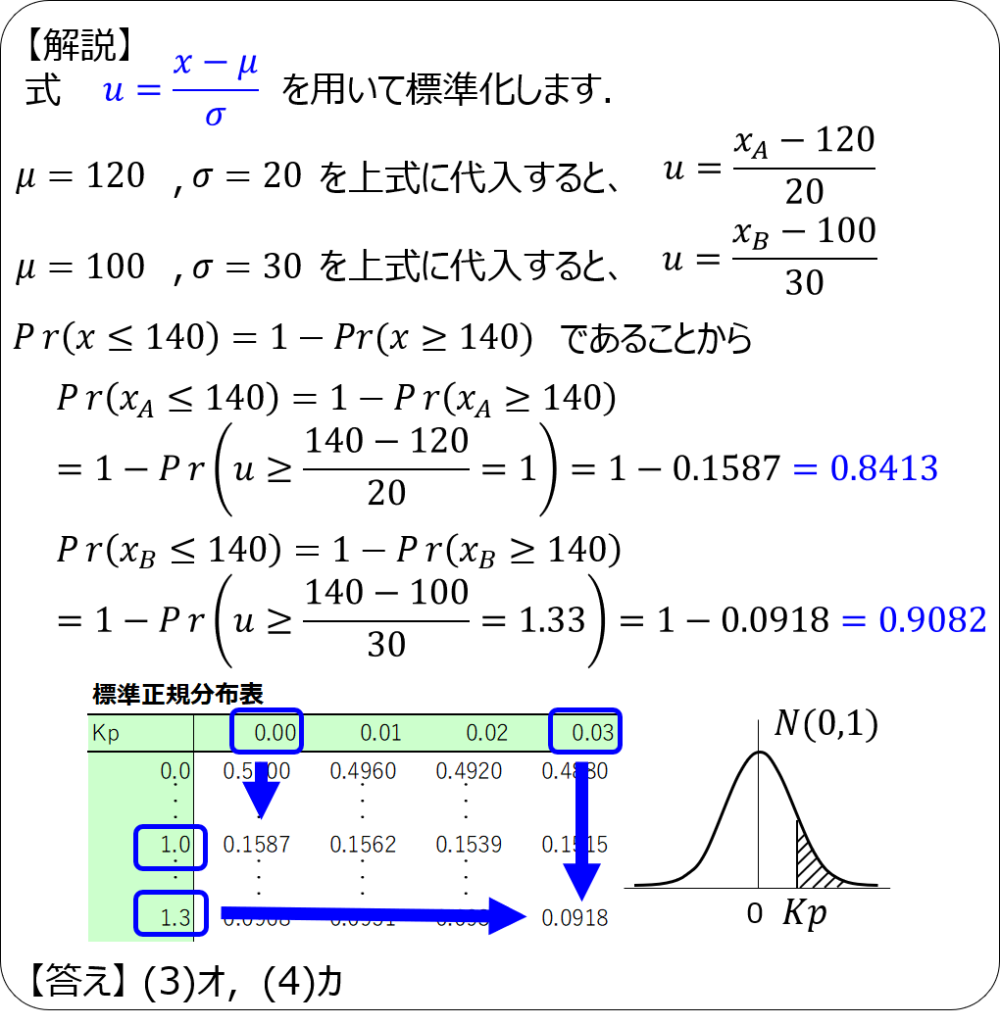
解説3

解説4

その他の模擬問題の一覧はこちらをどうぞ。

なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。





コメント