「エクセルを使って回帰分析をやりたい」
「アドイン機能は知っているが結果の見かたが分からない」
「エクセル関数を使って自力で計算できるようにしたい」
このような疑問や悩みをお持ちの方に向けた記事です。
いまや、エクセルの機能を使えば、複雑な統計の計算も一瞬で答えを導き出すことができます。
特に、回帰分析のような一般的に広く使われる手法の場合、エクセルのアドイン機能としてツールが用意されており、データ範囲を選ぶだけで計算ができる優れものです。
しかし、その便利さの反面、どのような計算を経て答えが導き出されているのか、得られた答えは有意なものなのか、初心者では判断が付かないケースも多いと思います。
この記事では、エクセルを用いた統計処理として、アドイン機能を使った回帰分析の結果の見かた、エクセル関数を使った計算方法について解説しています。
ぜひ、最後まで読んで参考にしていただければと思います。
回帰分析とは?
まず、回帰分析とは何か、基本的なところを整理しておきます。
回帰分析とは、要因となる変数と結果となる変数の関係性を明らかにし、両者の変数を一つの関係式に表す統計的手法のことです。
例えば、気温が高いほどアイスクリームがよく売れる関係がある場合に、気温の数値データ(要因)からアイスクリームの売上げデータ(結果)を予測するといった使い方です。
要因となる変数$x$を説明変数、結果となる変数$y$を目的変数と呼び、$y=β_{0}+β_{1}x$の関係式のことを回帰式と言います。
$β_{0}$と$β_{1}$は回帰係数と呼び、グラフの傾きにあたる要素を$β_{1}$、縦軸と交差する切片の値を$β_{0}$と表記します。

また、説明変数は必ずしも1つである必要はなく、2つ以上の変数で構成することも可能です。
説明変数が1つの場合を単回帰分析、2つ以上の場合を重回帰分析と呼び、重回帰分析は多次元の変数を取り扱う多変量解析の一種と言えるのです。
詳しくは以下の記事で解説していますので、合わせてご覧いただければと思います。

回帰係数の定義
$β_{0}$と$β_{1}$は以下の式で計算することができます。

基本的には$β_{1}$を先に求めて、続けて$β_{1}$を代入して$β_{0}$を計算します。
$x$と$y$の平均値、偏差(各データと平均値との差)平方和が分かれば簡単に求められるので、計算自体は特に難しいものではありません。
後ほど詳しく説明しますが、平均値だけでなく、偏差平方和もエクセル関数がありますので、エクセルのアドイン機能を使わなくても、簡単に回帰式を求めることができます。

ほとんど関数で計算できるんだね
分散分析
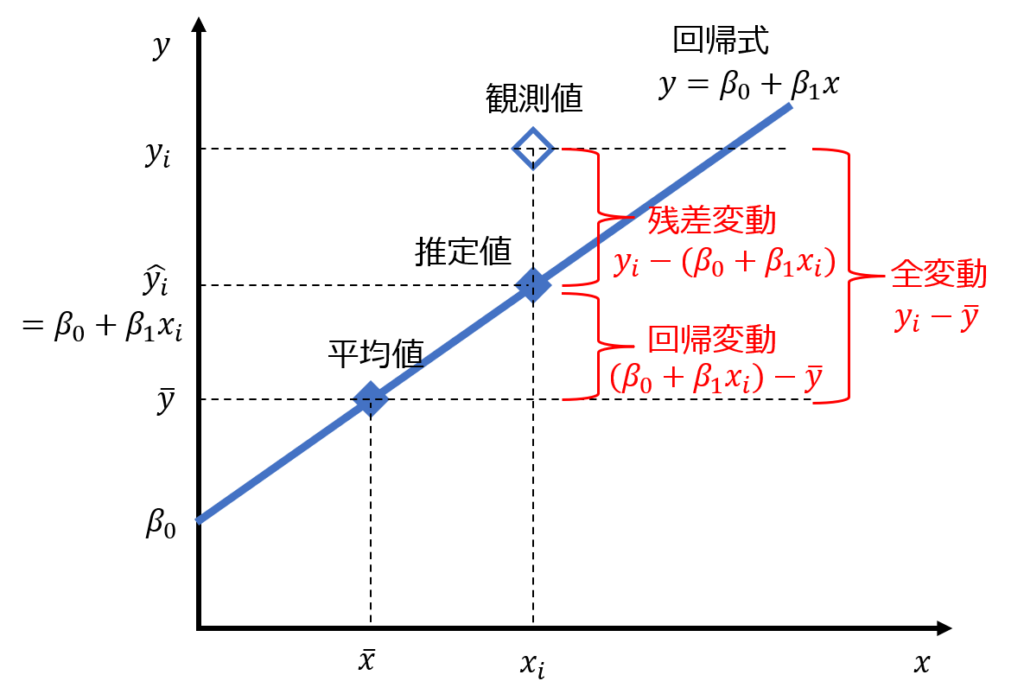
分散分析とは、回帰式の有意性を統計的に検証するための手法で、回帰変動と残差変動の分散比を検定統計量として、F検定により有意性を判別します。
全変動:実際のデータと全体の平均値との差
回帰変動:回帰式から得られた推定値と全体の平均値との差
残差変動:実際のデータと回帰式から得られた推定値との差
全変動=回帰変動+残差変動
分散分析も基本的には偏差平方和と四則演算を合わせた程度の計算なので、さほど難しいものではありません。
しかし、分散分析では、回帰変動や残差変動といった聞きなれない用語、さらには有意Fやt値、P値といった統計的検定に付きものの用語が多く登場します。
そのため、思わず回帰係数や相関係数といった欲しい結果だけに着目しがちになり、実は誤差成分が大きく、精度が不十分であったなんていう見落としも少なくありません。
毎回自分で計算する必要はありませんが、計算方法やポイントとなる着目点はきちんと押さえておくようにしましょう。
なお、統計的検定や確率分布に関する基礎知識から詳しく知りたい方は、以下の記事で解説していますので、合わせてご覧ください。



アドイン機能を用いた回帰分析の方法
まず、もっとも手軽な方法として、アドインの「データ分析」ツールを用いることが挙げられます。
「データ分析」ツールは、回帰分析や統計的検定などの主要な統計的手法に関して、データ範囲といくつかの前提条件を指定すれば、自動で計算してくれる大変便利な機能です。
手順
アドイン機能を有効にする
まず、Excelの設定をしましょう。
「ファイル」→「その他」→「オプション」を選択します。
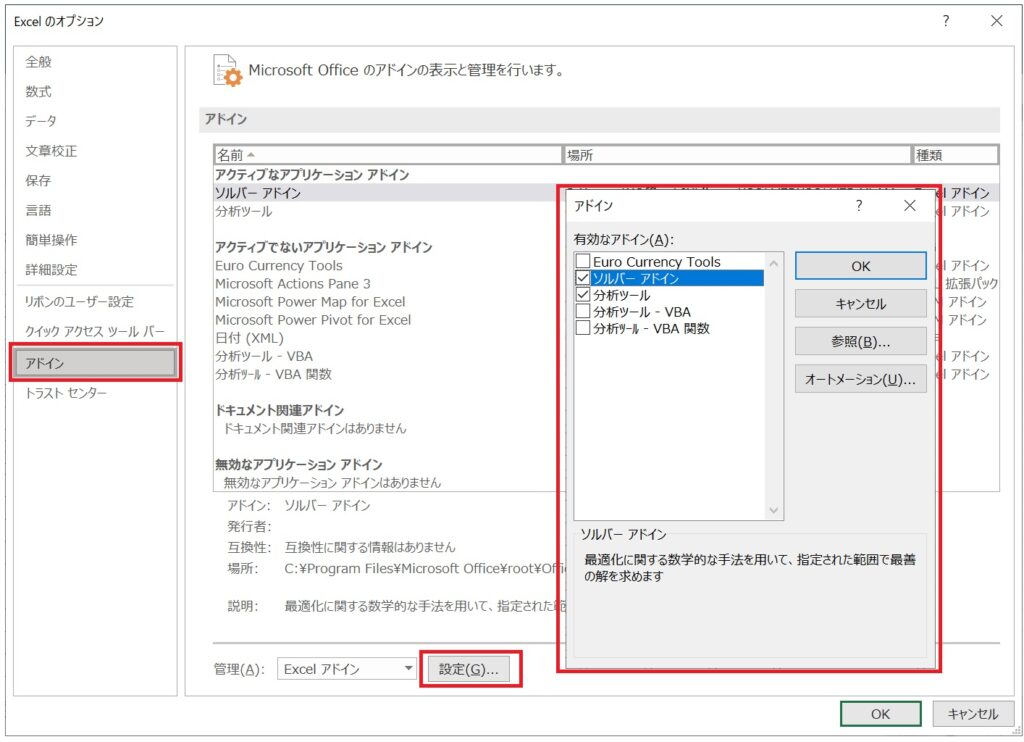
「アドイン」→「設定」を指定し、「分析ツール」にチェックを入れて有効化します。
データ範囲と前提条件を指定する
次に、アドイン機能を用いて回帰分析の演算をします。
「データ」タブの「データ分析」をクリックし、「回帰分析」を選択します。
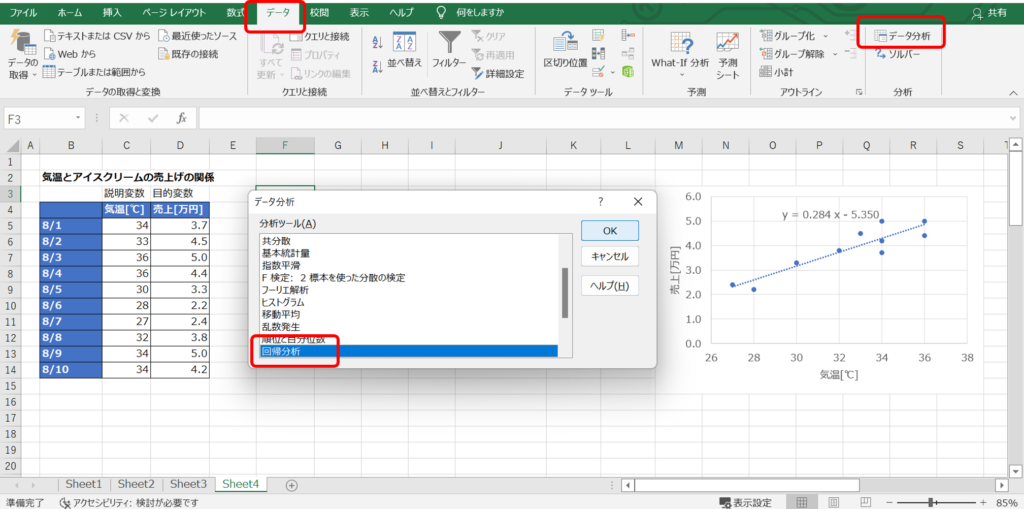
「入力Y範囲」に目的変数とするデータ範囲、「入力X範囲」に説明変数のデータ範囲を指定します。
単回帰分析では説明変数は1つですが、重回帰分析の場合も同じで「入力X範囲」に複数列の説明変数のデータ範囲を指定します。
定数に0を指定したり、任意の有意水準を設定したりできますが、特殊な制約事項を設けない限りは使う必要はありません。
しいて挙げるなら、有意水準を99%に設定するくらいで、デフォルトで95%の結果が出力されるので、99%にチェックを入れておけば、95%と99%の両方を出力できます。
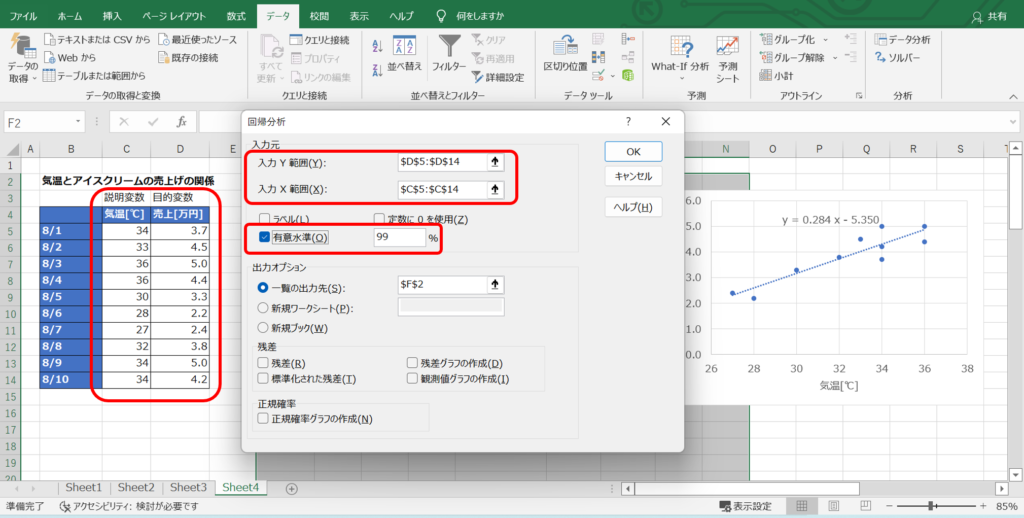
また、「データ分析」ツールでは、残差グラフや標準化残差、正規確率グラフの作成もチェックボックスを入れるだけで出力できる優れものです。
これらは、回帰モデルの妥当性を検証する手段の一つで、特に重回帰分析のような複雑な計算が必要な場合には重宝します。
ただ、単回帰分析ではいずれも手計算で簡単に求められる他、分散分析表で主要な考察は十分にできますので、ここでは省略します。

ほんと簡単に結果が出てくるんだ
結果の見かた
データ範囲を指定してボタン一つで簡単に回帰分析ができるのは良いことですが、出力された結果を見て、専門用語の多さに驚いた方も少なくないと思います。
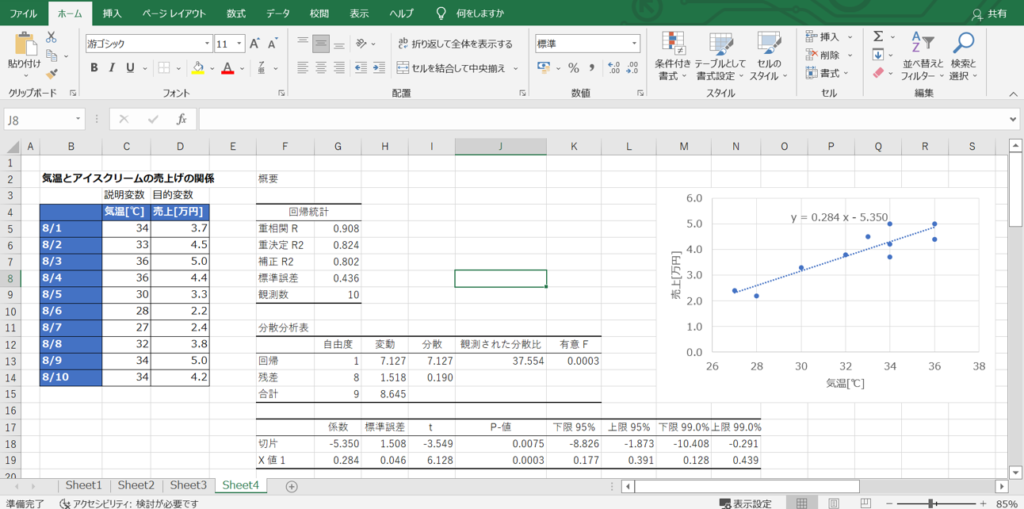
そして、用語の解説がないので、それぞれ何を表しているのか、自力で紐解いていかねばなりません。
後ほど、詳しい計算方法を説明しますので、ここではまず用語の意味と主要な確認ポイントについて解説します。



確認すべきポイント
どの項目を確認して、何を基準に良し悪しを判定すれば良いのか、初見では難しいと思いますので、重点的に確認すべきポイントを次に紹介します。
- 重相関R:相関係数のこと
- 有意F:分散比をF検定したP値
- 回帰係数:切片とX値
- P-値:回帰係数をt検定したP値
- 下限95%値、上限95%値:回帰係数の信頼区間
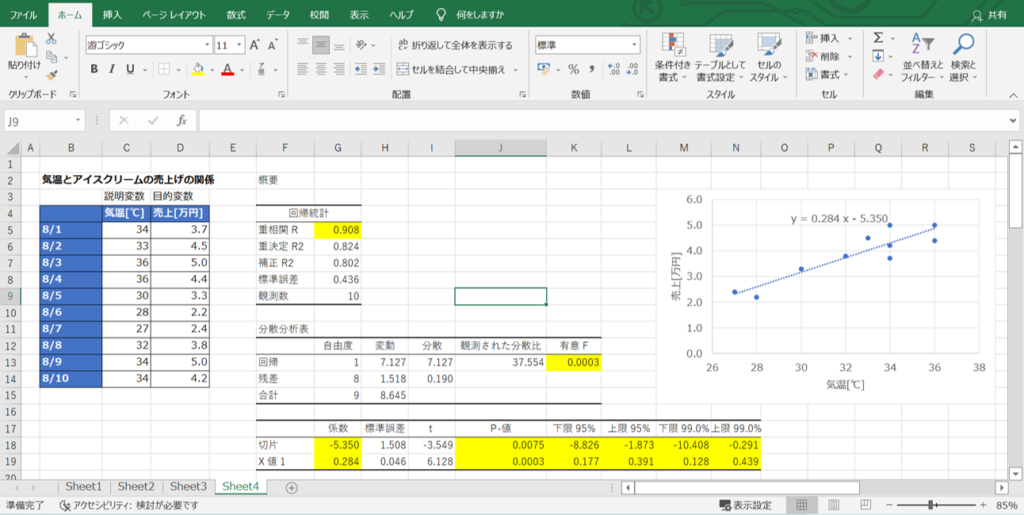
重相関R
いわゆる相関係数のことで、単回帰分析の場合でも重相関Rと記載されます。
変数どうしの関係の強さを表すもので、以下の値を目安に関係の有無を確認しましょう。

また、重決定係数R2は相関係数の二乗で求められる値なので、相関係数が高ければ決定係数も高くなり、どちらか片方の確認だけでも問題はありません。
有意F
分散分析表で最終的に計算したいのは、回帰変動と残差変動の分散比です。
そして分散比は自由度によって有意判定が下される基準が異なるので、自由度と分散比からF分布の確率に変換したものが「有意F」というわけです。
つまり、有意Fの値は確率を表しており、この値が小さいほど滅多に起こらない事象であることを意味します。
F検定では、帰無仮説として「2つの母分散に違いがない」と仮定するので、有意Fの確率が小さいことは帰無仮説が棄却されるということになります。
回りくどい言い方になりましたが、結局のところ、回帰変動が残差変動に対して十分に大きく、回帰式で説明可能な成分が大きいことを意味しているのです。
有意Fの判定の目安は、0.05(5%有意水準)または、0.01(1%有意水準)を用いるので、これよりも小さい値であるか否かを確認するようにしましょう。
回帰係数
回帰係数は、切片とX値という名称で出力されます。
回帰係数の値に判定の目安はありませんが、求めたい回帰式として妥当な係数なのか、確認するようにしましょう。
例えば、切片がマイナスになることがあり得ないような事象の場合、仮に$β_{0}$がマイナスの結果が出たとしたら、元のデータの測定方法やデータ入力にミスがあるかもしれません。
P-値
P値は回帰係数の有意性を調べるための指標で、$β_{0}$、$β_{1}$それぞれに対して、t検定から得られた検定統計量に対応する確率の値です。
先ほどの有意Fと同様に値が小さいほど精度が高いことを示し、P値の目安も0.05や0.01を基準とします。
反対に、この値が大きい場合、回帰係数の推定誤差(標準誤差)が大きいことを表しており、すなわち回帰式から得られる推定値もばらつきが大きいことを意味しています。
下限95%値・上限95%値
これらは回帰係数の信頼区間を表しています。
つまり、回帰係数の出力値である$β_{0}$と$β_{1}$を平均値(期待値)とした上下のばらつきの範囲を意味しており、95%の確率で示された値の範囲内に収まるということです。
先ほどのP値と同様に、回帰係数の標準誤差が大きいと信頼区間の範囲も広くなりますので、回帰式の精度を確認する方法の一つとして覚えておきましょう。
エクセル関数を用いて自力で解く方法
さて、ふたつ目の方法は、エクセルの関数を駆使して自力で回帰分析を行う方法です。
先ほどのデータ分析ツールは大変便利ですが、数値しか出力されないために、それぞれの項目がどのような計算で得られたのか、どの項目どうしに繋がりがあるのか分かりません。
計算の根拠を理解せずに使うと、結果の妥当性を判断する際にも見落としに繋がりますので、ぜひ一度は計算方法を理解しておくことをおススメします。
手順
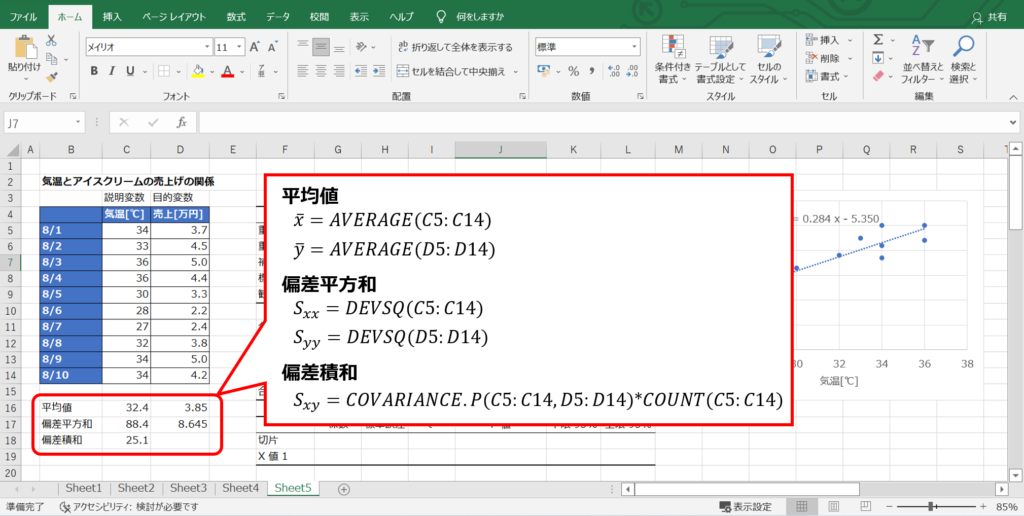
平均値と偏差平方和を求める
まず、説明変数と目的変数のデータから平均値($\bar{x}$, $\bar{y}$)と偏差平方和($S_{xx}, S_{yy}$)偏差の積和 ($S_{xy}$)を求めます。
以下の関数を用いると手間を省いて計算できます。
平均値($\bar{x}, \bar{y}$):AVERAGE関数
偏差平方和($S_{xx}, S_{yy}$):DEVSQ関数
偏差積和($S_{xy}$):COVARIANCE.P関数×データ数
偏差積和を直接求める関数がないので、共分散を求めるCOVARIANCE関数にnをかけて求めます。
分散分析表を作成する
決定係数や標準誤差などの項目は分散分析表の値から計算されるので、回帰統計の項目を埋めるよりも先に分散分析表を作成します。
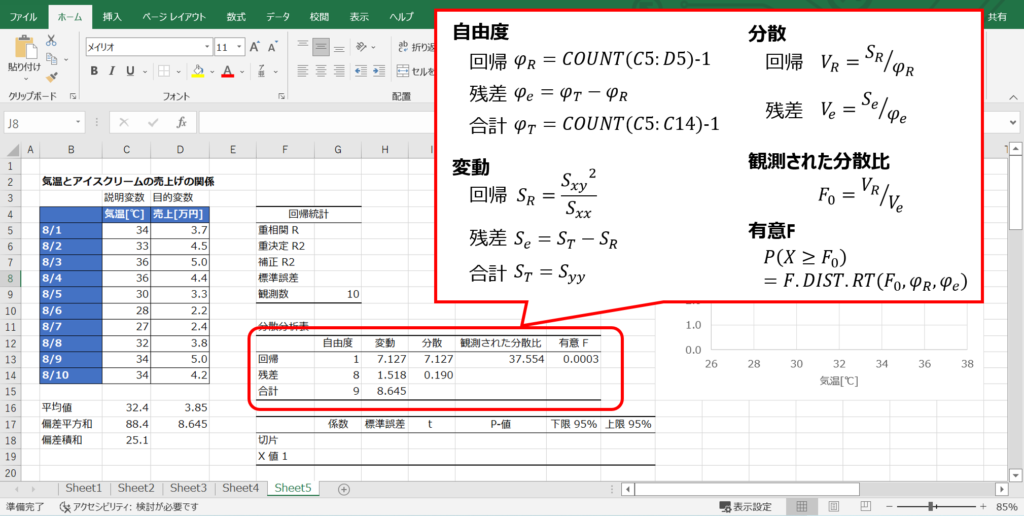
有意Fで用いるF.DIST.RT関数は、F分布の上側確率(右側確率)を返す関数で、検定統計量(分散比)と自由度を設定すれば、対応する確率を求めることができます。
回帰係数の検定と信頼区間の表を作成する
回帰係数、標準誤差、t値は、次の計算式で求めることができます。
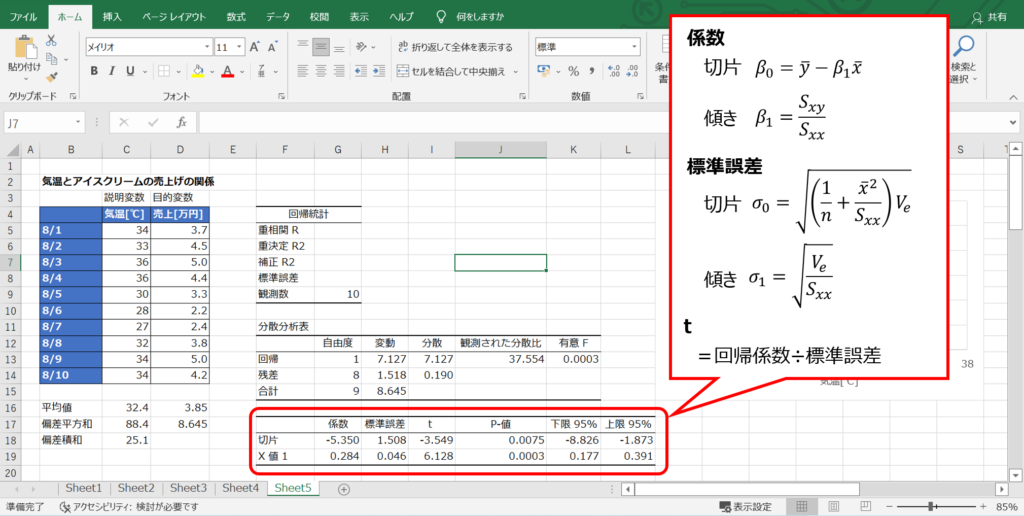
標準誤差は切片と傾きでそれぞれ計算式が異なりますが、分散の加法性の法則から導き出すことができます。

P値は検定統計量tに対応する確率で、残差変動の自由度とt値からT.DIST.2T関数(t分布の両側確率を返す関数)を用いて計算できますが、ここで一つ注意点があります。
t値が正の場合には、そのまま入力すれば問題ないですが、この関数はt値が負の場合には対応していないので、マイナス1を乗じて正の値に変換せねばなりません。
t値の符号を見て、その都度修正しても良いですが、一律で設定したい場合には、IF関数を用いると便利です。
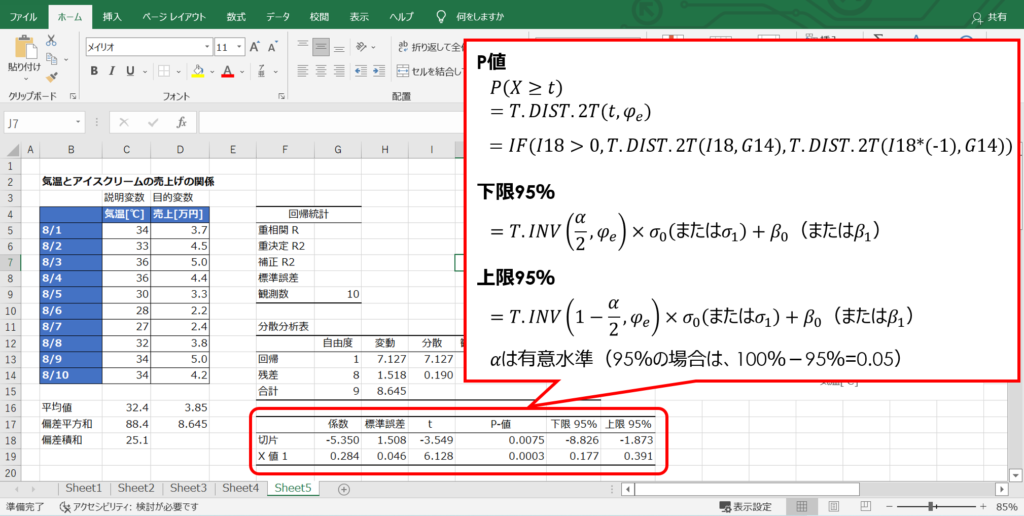
続いて、回帰係数の信頼区間を求めます。
T.INV関数はt分布の左側逆関数を返すもので、残差変動の自由度と信頼区間の確率を設定すれば、対応するt値を出力できます。
これに標準誤差(標準偏差のこと)を乗じて、期待値である$β_{0}$および$β_{1}$を加えると、信頼区間を求められます。
なお、T.INV関数は左片側確率を表すので、下限95%を求めたい場合は0.025、上限95%を求めたい場合は0.975を確率の値とします。
回帰統計表を作成する
最後に回帰統計表を作成します。
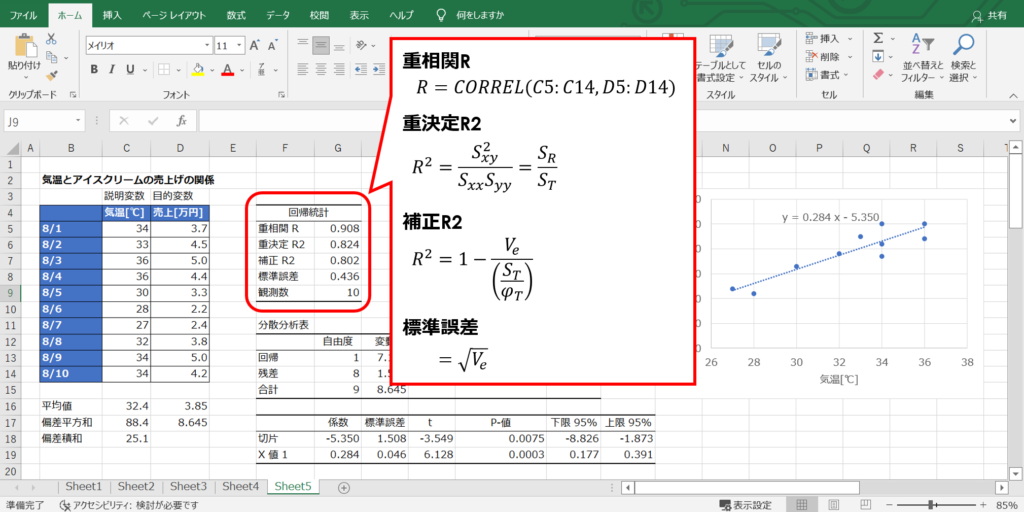
補正R2は自由度調整済み決定係数と呼ばれます。
回帰分析では計算式の構造上、説明変数の数が多いほど決定係数が高くなる性質があり、目的変数に寄与しない変数であっても、多いほど結果が良く見えてしまいます。
補正R2は、これを修正するために変数の数(自由度)に応じて決定係数を下げるように調整がなされたものなのです。
以上で、データ分析ツールと同じ表を関数の計算だけで作成できました。
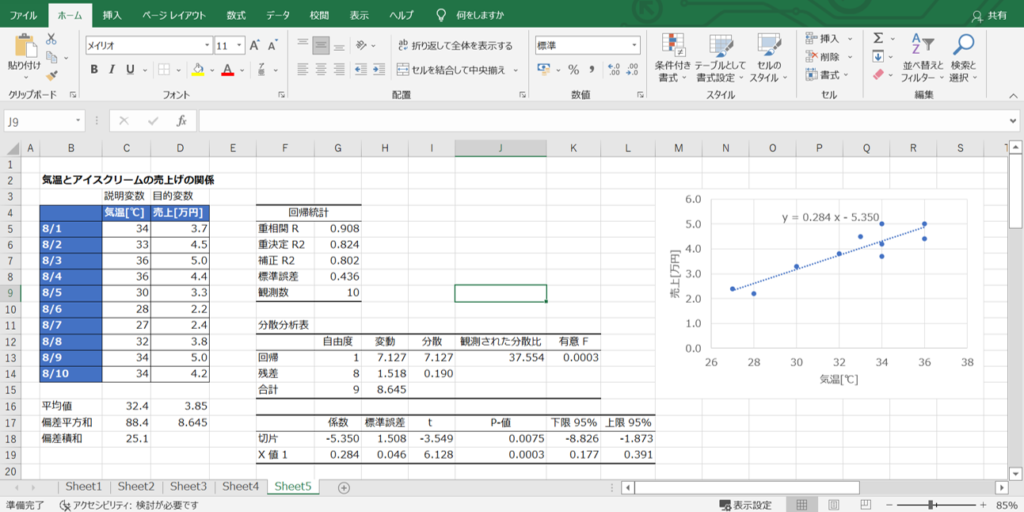

自力で計算できれば応用もバッチリだね
まとめ
- 回帰分析で重点的に確認すべきポイント
・重相関R:相関係数のこと
・有意F:分散比をF検定したP値
・回帰係数:切片とX値
・P-値:回帰係数をt検定したP値
・下限95%値、上限95%値:回帰係数の信頼区間 - エクセル関数を用いて自力で解く方法
・平均値と偏差平方和を求める
・分散分析表を作成する
・回帰係数の検定と信頼区間の表を作成する
・回帰統計表を作成する - 使えると便利な関数
・AVERAGE関数:平均値を求める
・DEVSQ関数:偏差平方和を求める
・COVARIANCE.P関数:共分散を求める
・F.DIST.RT関数:F分布の上側確率(右側確率)を返す
・T.DIST.2T関数:t分布の両側確率を返す
・T.INV関数:t分布の左側逆関数を返す
最後までご覧いただきありがとうございました。
まずは相関分析の基本から始めたい方に。
相関分析から単回帰・重回帰分析まで幅広く。
多変量解析マスターを目指すなら。




コメント