「母集団と標本の違いを知りたい」
「品質管理の場面で標本調査をどう活用するのか」
「標本調査には、どのようなメリットがあるのか」
このような疑問・悩みをお持ちの方に向けた記事です。10分で理解できるよう、わかりやすく簡潔に解説します。
前の記事では、品質管理におけるデータ解析の必要性について説明しました。
モノづくりの現場では、品質のばらつきを避けては通れず、事実を客観的に捉えて、ばらつきをコントロールすることが重要です。
しかし、実際の現場では、収集できるサンプルや時間に制約がある中での判断が求められます。
そのためには、適切なデータ収集、分析、解析が肝心で、その基本的な例として、QC7つ道具や新QC7つ道具が挙げられます。
この記事では、サンプリングの進め方の前段階として、品質管理における標本調査の有効性について解説しています。
調査の種類

アンケートも調査のひとつだね
サンプルの選び方によって、全数調査と標本調査に分けられます。
全数調査の分かりやすい例は国勢調査で、一部を選んだ場合に生じる誤差がなく、正確なデータを取得できます。
人口や男女比、年齢構成などを正確な調査結果が得られるメリットがありますが、その反面、膨大な労力、時間、コストがかかります。
全体から一部を選ぶ標本調査の身近な例には、選挙の開票速報があります。
開票の直後に当選確実が表示されて、なぜ?と疑問に思うことはありませんか。
出口調査の結果を元に予測するにしても、いったい何人に調査して、どのくらいの信頼度で発表されるのか、不思議に感じたことがある方も多いと思います。
これは、統計的な計算から導き出した条件を元に、無作為に選ばれた投票者から事前に聞き取りした結果から判断されるものです。
実際に投票した内容と異なる回答をする可能性や、都合により当日に投票に行けない場合もあります。
そういうケースでは、本当に投票した事実と異なるアンケートになりますが、一定の割合でこういった誤差を織り込んだ結果として当確が出されるわけです。
実際に、投票者の全員に対して、投票直後にアンケートを取っていると、膨大な労力とお金が必要です。
さらには、集計結果がそもそも開票時刻に間に合わない可能性もあります。
このような場合に、標本調査が効果を発揮します。
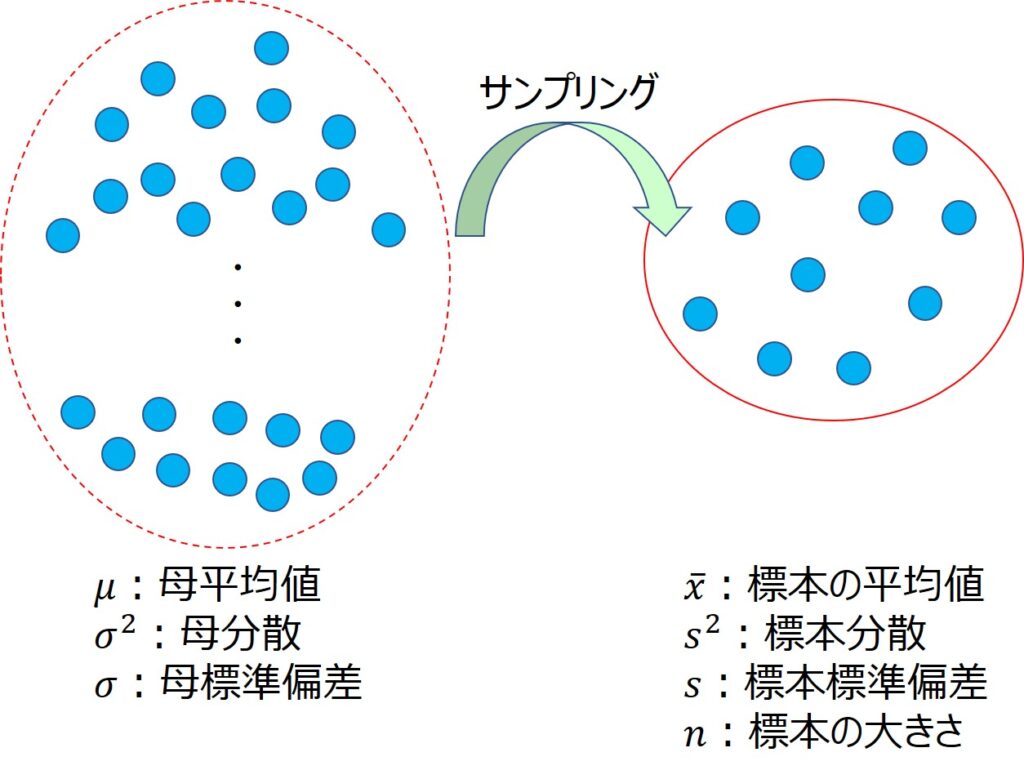
調査の対象全体を母集団、そこから一部分を選んだものを標本といいます。
関係を図示すると、以下のようになります。
なぜ品質管理で標本調査が有効か?
メリットと活用例
省力化、時間短縮、コスト削減が、メリットとして挙げられます。
品質管理の場面での活用事例をいくつか紹介します。
事例①:初品確認
毎日の生産で最初に作った一台目の出来栄えを確認することも、標本の抽出にあたります。
生産現場では、材料ロットの切り替わりや、設備の調子、あるいは意図しない環境の変化など、多くのばらつき要因が潜んでいます。
いつ、どのような状態で作られたのか素性の不明なサンプルから、いま現在の品質の状態を推定することは困難です。
しかし、一日の生産のかたまりに焦点を当てると、設備や環境はほぼ変化のない状態に統一され、ばらつきの少ない集団として解釈できます。
その代表として、初品の品質を確認することで、その日に生産するモノの状態を推測し、生産着手の可否を判断できます。
事例②:抜取確認
例えば、破壊強度試験のような場合では、その日の製品の出来栄えを直接的に確認できるため、健全性の把握に効果的です。
しかし、製品をすべてを破壊して確認するわけにはいかず、代表的なものに絞らなければいけません。
運用の一例としては、同じ日に生産したロットに対し、その中から標本を抽出して破壊試験を行い、その日に集団の全体を保証する考え方が抜取検査です。
事例③:トレンド管理
時間軸に対してサンプリングするのがトレンド管理です。
日々の検査で抽出した標本を並べて、時系列に対する傾向を調査し、異常の兆候を見つける使い方もあります。
QC7つ道具で使う管理図はトレンド管理に有効な手法であり、例えば毎日の初品データを取るなど、できるだけ時間軸以外のばらつきを抑えて抽出することが望ましいです。

やっぱり、ぜんぶ調べるのは大変だ・・
母集団を推定する
2つの誤差
①:標本誤差
標本と母集団の統計量が完全に一致することはなく、必ず誤差が生じます。
両者の差を標準誤差といい、英語ではsampling errorと呼ばれています。
②:非標本誤差
標本誤差以外のものを非標本誤差といいます。
例えば、アンケート調査などでは、未回答や誤回答があります。
製造現場の例では、測定誤差が非標本誤差の代表であり、計測器のずれや、測定方法のばらつきなどに起因する誤差を表します。
標本誤差と信頼区間
標本調査の目的は、全体の把握ですが、あくまで推定値であり、真値と完全には一致しません。
つまり、推定値には幅があり、例えば、「母集団の平均値は○○%の確率で、△△~□□の範囲に入る」という表し方をします。
ここで、△△~□□の範囲のことを信頼区間と呼び、推定値を算出することを区間推定と言います。
95%信頼区間の場合、以下の数式を用います。

2.262は、n=10の95%信頼区間を求める場合の係数で、t分布表から導き出します。
生産現場では、母集団の標準偏差が分からないことが多いので、この式を使うことが多いです。
参考までに、母集団の標準偏差が既知の場合は、以下の数式で求められます。

1.96という値は、標準正規分布表から求めます。
どの程度の標本数が必要か?
さて、それでは早速、標本を抽出して全体の状態を推定してみましょう。
・・といっても、いったいどの程度のサンプルを集めたらよいのでしょう?
これには明確な答えはなく、ケースバイケースとしか言えませんが、さすがにそれでは何の参考にもならないので、計算の具体例を交えて目安のイメージをお伝えします。
まず、あらためて式1を見ると、nの数を増やすと信頼区間を狭められることが分かります。
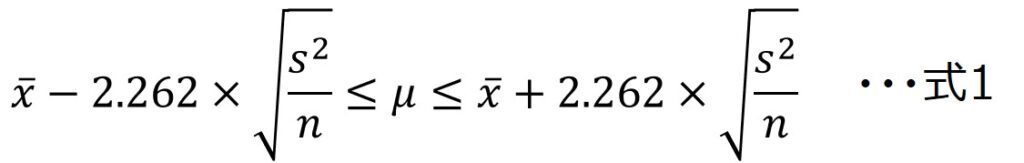
ここで計算の具体例を挙げて説明します。
例えば、以下のような分布の標本データを題材にします。
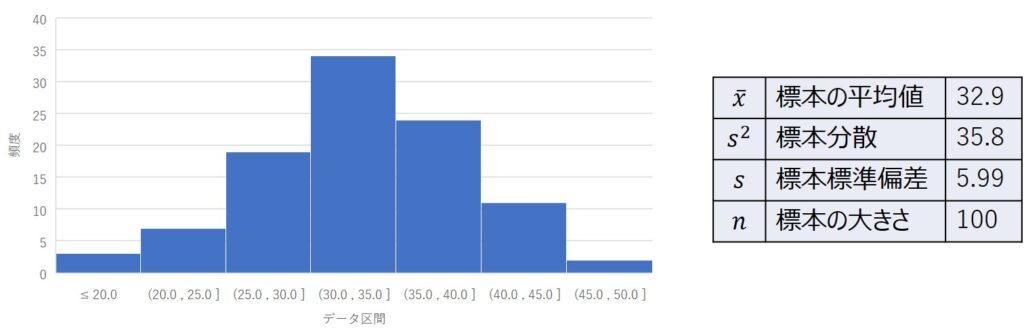
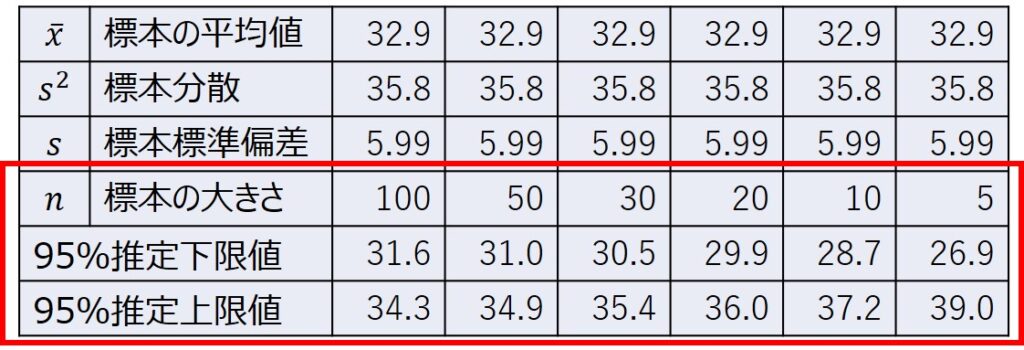
これを式1に当てはめると、信頼区間を以下のように算出できます。
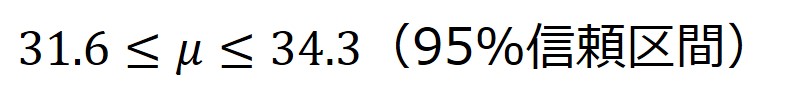
推定精度が十分かどうかは、それぞれの事情によりますが、標本の平均値32.9に対して、±1.4の誤差と考えれば、許容範囲かどうかイメージしやすいと思います。
さらに、n数を変えたときに、信頼区間がどう変化するか見てみましょう。
n=100から減らしていくと、信頼区間が徐々に広がっていき、n=5の場合には、±6.0の誤差となります。
信頼区間をエラーバーにして図示すると、このようになります。
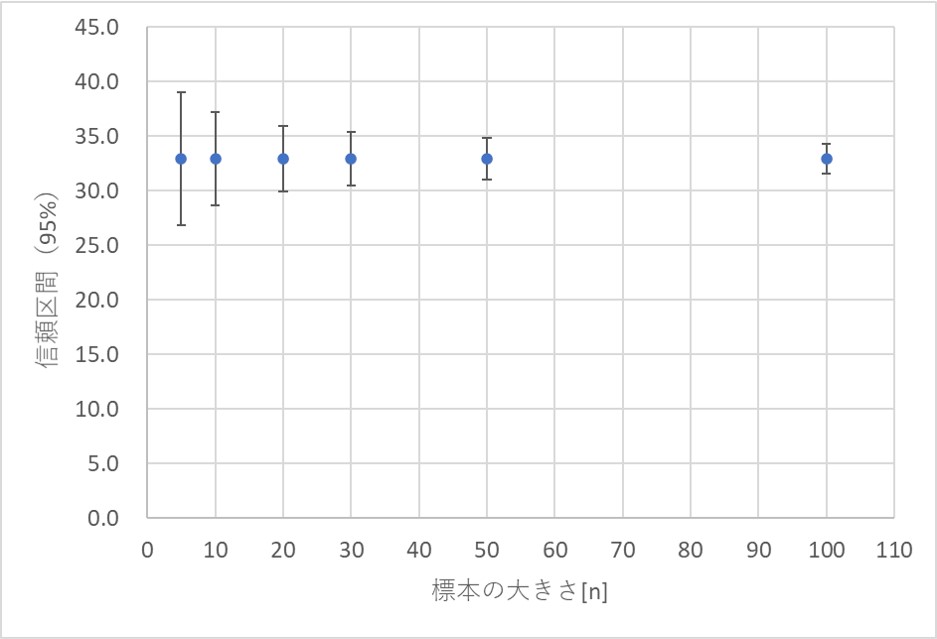
nが一桁の場合は、変化が著しいですが、50から100にかけては変化が小さく、それ以上になるとさらに小さくなります。
サンプルサイズを増やす方が推定の精度は上がりますが、その分だけ調査に労力と時間がかかりますので、調査を始める前に、適切な数を決めておきましょう。

20個でも、けっこう精度あるんだね
なお、式1を見て分かる通り、n数を増やす他に、ばらつきを小さくすることでも、信頼区間を狭められます。
ただし、そもそも狙ってばらつきを変動できない場合も多く、さらに何割も下げることは至難の業です。
反対にサンプルサイズであれば、精度が低い場合には増やせばよいので、柔軟に調整できる要素です。
ばらつきに関しては、調査したい集団のばらつきが小さい場合は、必要なサンプルが少なくて済む、という程度に捉えておくとよいでしょう。
標本調査の種類
有限母集団と無限母集団に分けられ、集団の大きさが決まっているかどうかで分類されます。
無限母集団には、日々、生産を継続する場合が例に挙げられます。
現時点までのデータに限定すれば有限ですが、これから先にも蓄積され続けることを考えると、集団の数は無限に広がっていきます。
そういう場合は、以下の式で算出する不偏分散(v2)を母分散(ばらつき)の推定値として扱います。
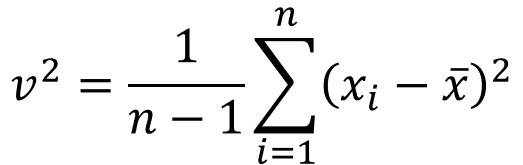
ちなみに、標本の分散は以下の式なので、n/(n-1)をかけた値が不偏分散となります。
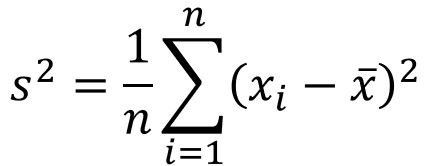
標本を選ぶ際に、必ずしも最大値や最小値が含まれる保証はなく、ばらつきを低めに見積もってしまう性質があります。
不偏分散は、これを補正するための換算式です。
こてつ経験談
リピート生産の落とし穴
私の過去の経験で、標本調査の教訓となった事例を紹介します。
とある製品の品質トレンド調査をしており、その製品は長年作り続けているもので、いわゆるリピート生産の品種でした。
数量規模は変動するものの、製造フローや装置など、基本的には同じ状態で生産を維持するもので、品質の安定化が求められていました。
そこで、まずは製品の出来栄えの実力値を確認するため、過去の生産データをすべて集計しました。
さすがに、リピートの品種だけあって、過去データは豊富に蓄積されており、統計量を算出するには十分すぎるくらいの膨大な量が残っていました。
平均値やばらつきなど、製造時期で分類してみたり、あるいはヒストグラムで分布を見たり、QC7つ道具をいろいろと活用して、データ解析を行いました。
そして、当時の結論として、規格値に対して十分に余裕があるため問題なし、と導き出し、調査を終了しましたが、その先に落とし穴がありました。
その後の生産で、徐々に平均値がシフトしはじめ、やがて規格を逸脱するレベルに到達してしまったのです。

地道な調査の継続が大事
実は、あとで分かったのですが、部品の調達元が、こっそりと材料を類似の安価なものに変えており、いわゆる「サイレントチェンジ」が行われていました。
平均値が刻々と変化していくことに全く気付かず、このような始末になってしまったわけです。
まさに、無限母集団の性質を見落として、過去の有限なデータしか見ていなかったことが失敗の種でした。
これまでの状態が問題ないからといって、今後も同じ傾向が続く保証はありません。
日々のトレンドモニタや、定期的な工程のチェックなど、地道な調査を継続することの重要性が身に染みた経験でした。
最初は上手くいってたのに・・と後悔しないよう、いつどんな変化がくるかもしれないと、常にアンテナを張ることが不具合を未然に防ぐことに繋がります。
まとめ
- 母集団:調査対象の全体
- 標本:集団を代表する一部分
- 標本調査のメリット
⇒省力化、時間短縮、コスト削減 - 生産現場での活用例
⇒初品確認、抜取確認、トレンド管理
標本調査は効率的に労力と時間を減らせる強力な手法です。
必要十分な精度が得られるか、サンプルサイズをキチンと確認して活用していきましょう。




コメント