「復元抽出って何?」
「非復元抽出と何が違うの?」
「有限母集団修正の影響を知りたい」
このような悩みをお持ちの方に向けた記事です。10分で理解できるよう、わかりやすく簡潔に解説します。
母集団と標本の記事では、有限母集団と無限母集団について解説しました。
集団の大きさが決まっているかどうかで分類され、大きさが無限の事例としては、日々、生産を継続する場合などが挙げられます。
有限母集団の事例には、生産ロットなど数が決まっているケースが挙げられます。
そして、このような有限の集団からサンプルを採取する場合、抜き取るたびに母集団の数が変わるので、注意が必要です。
この記事では、有限母集団からサンプリングする際の注意点について、計算の具体例を交えて解説します。
補正のイメージを掴みやすくなると思うので、ぜひ参考にしていただければと思います。
復元抽出と非復元抽出
母集団から選んだサンプルを一度もとに戻すか、戻さないかで分類されます。
元に戻してから次を選ぶ場合、何度選んでも元の集団の数は変わらず、同じ前提条件で選ぶことになります。
一方、元に戻さない場合は、抜き取るたびに母集団の数が減少します。
母集団の大きさが変わると、母分散も変動します。
そして、母分散が変わると、これを用いて計算する標本平均の分散も変動し、区間推定の範囲の計算結果にも影響を与えます。
特に、母集団の数(N)が少ない場合や、標本の数(n)が多い場合、すなわちn/Nが大きい場合には影響が大きくなるので、注意が必要です。
有限母集団修正とは

むずかしそうな言葉・・
計算のしかた
サンプリングによる母集団の減少の影響を補正(修正)するための考え方で、以下の計算式で標本平均の分散の値を補正できます。
計算はシンプルで、元の値σ2/nに、補正係数として(N-n)/(N-1)をかければ良いのです。

補正の影響
ここで、補正の影響について、計算の例を交えて具体的に見てみましょう。
以下の表は、Nとnの値に対応する補正係数の計算結果です。
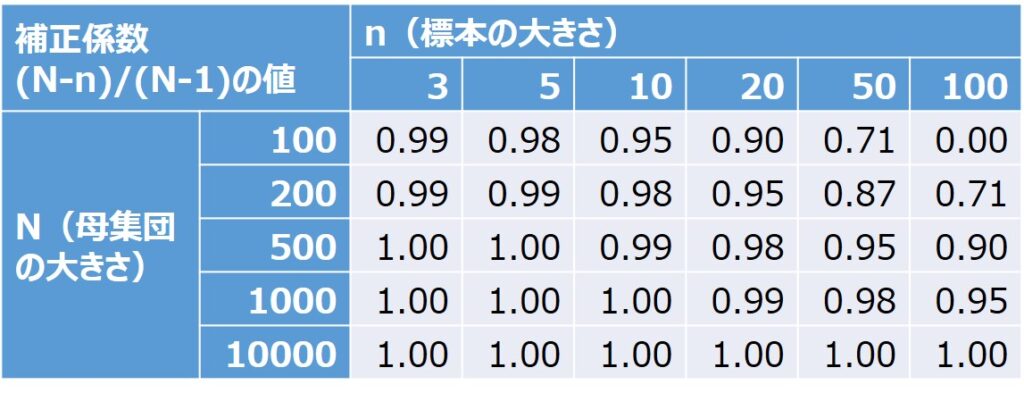
横軸にn、縦軸に補正係数、Nの大きさで系列を分けてグラフにすると、以下のようになります。
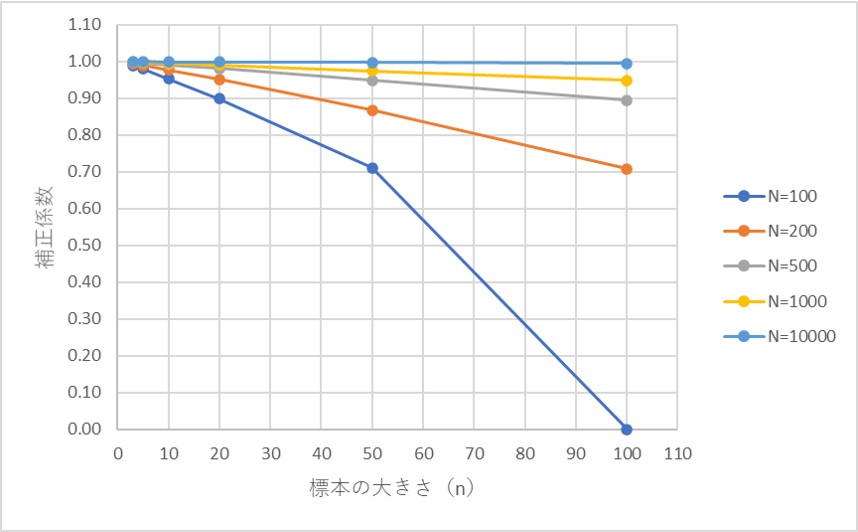
Nが小さいほど、補正係数が1から離れる、すなわち、補正の影響が大きいことを意味します。
また、nが大きい場合も、補正係数が1から離れていきます。
つまり、n/Nが大きいほど、補正の影響が大きいことがグラフからも見て取れます。
例えば、N=100の場合、nが10以下なら、補正係数は0.9以上で影響度は10%も無いことを意味します。
しかし、nが50を超えると補正係数は約0.7になり、30%も影響を与えるので、区間推定の範囲を求める上で、単純に無視するわけにはいきません。
ちなみに、Nが∞に近づくと、補正係数は1に収束します。
これは母集団の大きさが無限の場合、つまり、無限母集団を意味しており、このような補正の不要であることが、計算式からも分かります。
また、n=N(例えば、n=N=100)の場合、補正係数はゼロになります。
n=Nというのは、母集団のすべてのサンプルを採取する全数調査を意味しており、標本平均は母平均と一致するので、分散(ばらつき)がゼロと同じことを表しています。

ぜんぶ調べるのは全数調査だったね
採取する比率の目安
それでは、母集団の大きさに対し、どの程度の比率でサンプルを採取する場合に補正の考慮が必要なのか、目安を見てみましょう。
以下は、横軸にn/Nの比率、縦軸に補正係数を取ったグラフです。
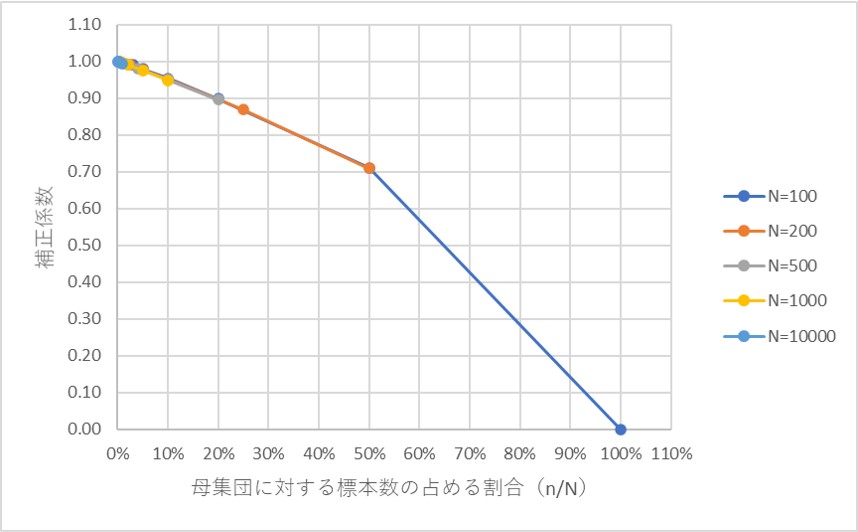
Nの大きさによらず、比率が10%の場合は約0.95、20%では約0.9、50%では約0.7と概ね同じ傾向であることが分かります。
厳密には、補正係数はNの大きさに影響を受けるので、ぴったり重なる訳ではないのですが、それよりも比率の影響の方が大きいということです。
n/Nの比率がどの程度の場合、補正係数としてどのくらいの影響があるのか、目安を覚えておくとよいでしょう。
こてつ経験談
日ごろから意識する?
ここまで、補正の計算方法や影響の大きさを説明しましたが、実は私自身の経験をもとに言うと、補正を省略したことによる致命的な失敗は特にありません。
そんな個人の話は当てにならないとか、じゃ何のために必要なのかと、ツッコミを受けそうですが、その意見はごもっともです。
ただし、あらためて計算式を振り返ると、母集団が減ることで、分散を多く見積もりすぎた分を補正する意味合いであることが分かります。
つまり、母集団に対して、多くの標本を調べたのであれば、精度良く区間推定できるはずであり、区間幅を狭めるための補正ということになります。
逆に言うと、補正を省略したことで、区間幅を広めに計算したとしても、悪めに見積もってしまうだけなので、平均値そのものが変わるわけではありません。
そもそも、サンプリングを行う際に、母集団に対する比率まで日常的に意識する方は、あまり多くないのではないでしょうか。
品質管理の現場では、標本調査はあくまで手段の一つで、得られた結果から対応策を検討し、効果を確認して・・と、PDCAサイクルを回していかねばなりません。
さらに、日々さまざまな問題が生じる中で、労力や時間の制約を考えていると、なかなか細部まで検討が及ばないこともあります。
なので、補正の影響を全く考えなくて良い訳ではないですが、まずは、補正の意味を理解して、影響の大きさをざっくりと掴んでおけばOKと思います。

不偏分散は要注意
集団の大きさによる影響を補正する意味合いでは似ていますが、不偏分散を考える際は注意が必要です。
母集団と標本の記事でも紹介しましたが、標本を選ぶ際に、必ずしも最大値や最小値が含まれる保証はなく、ばらつきを低めに見積もってしまう性質があります。
不偏分散は、これを補正するための換算式で、標本分散にn/(n-1)をかけた値となります。
nが十分に大きい場合は、補正係数は1に近づくので影響は小さいですが、例えば、nが10以下の場合は、影響が10%以上占めることになります。
分散から標準偏差を求め、これを元に管理範囲を規定する場合などは、数値そのものが規格値に反映されます。
検討段階で甘く見積もって、後々、痛い目にあうことのないよう、正しく使い分けをしましょう。
まとめ
- 復元抽出と非復元抽出
⇒母集団から選んだサンプルを一度もとに戻すか、戻さないかで分類する - 有限母集団修正
⇒サンプリングによる母集団の減少の影響を補正(修正)するための考え方
⇒標本平均の分散に、補正係数として(N-n)/(N-1)をかけ算する - 補正の影響
⇒n/Nが大きいほど、補正の影響が大きい
⇒N→∞で補正係数は1に収束(無限母集団と同じ)
⇒n=Nの場合、補正係数はゼロ(全数調査と同じ) - 補正係数の目安
⇒標本数の比率と補正係数の関係
10%:約0.95、20%:約0.9、50%:約0.7
※厳密には、Nの大きさによって変動
母集団が大きい場合には、結果的にほとんど補正の影響はありませんが、意味を知らずに統計量を取り扱うと、ふとした時に落とし穴があります。
正しく意味を理解して、必要な時に適切な補正計算ができるよう、下積みをキチンとしておきましょう。




コメント