この記事では、1つの母不適合品率の統計的検定(または計数値の検定と呼ぶこともあります)について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
なお、統計的検定の概念とメリット、登場する用語の意味など、統計的検定(その1)の記事から段階を追って説明しています。
さまざまな検定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

不適合品率とは?
定義
「不適合品」とは規格に適合しないもの、すなわち不良品のことを意味し、不適合品率とは不良品率のことを表します。
とある母集団から$n$個をサンプリングし、その中に$x$個の不良品が入っているとすると、不適合品率$p$は$x/n$となります。
ここで、サンプリングにより得られた不適合品率は「標本不適合品率」のことであり、統計学では「$\bar{p}$」と表記されることが多いです。
その一方、母集団の不適合品率を意味する「母不適合品率」は$p_{o}$と表記され、$\bar{p}$と区別して表現されます。
母不適合品率の検定は、標本データから得られた不適合品率$\bar{p}$と母集団の不適合品率$p_{o}$の差を調べるもので、サンプルサイズ$n$、不良数$x$から検定統計量を求められます。
二項分布との関係
成功か失敗(または良品/不良品)のいずれかで表される試行のことをベルヌーイ試行と呼びます。
ベルヌーイ試行を1回行う場合において、成功する確率を$p$とすると、失敗する確率は$1-p$となります。
そして、これを何回も繰り返した場合における成功回数の分布を二項分布と呼び、以下の数式で定義されます。
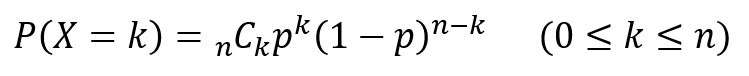
$n$は試行回数、$p$は成功確率、$k$は成功回数を表し、「確率変数$X$は二項分布$B(n,p)$に従う」と表現されます。

二項分布は統計学に欠かせないから必ず覚えておこう
二項分布は、不適合品率と密接な関係があります。
例えば、とある検査で不適合品が出現する状態を「成功」、出現しない状態(良品)を「失敗」と当てはめると、まさにこの検査はベルヌーイ試行と言えます。
そして、サンプルサイズ$n$、不適合品率$p$において、不良数$x$(二項分布の定義では$k$と表記)は、二項分布$B(n,p)$に従うと言えるのです。
そのため、母不適合品率の検定を行う際にも、二項分布の期待値や分散の考え方が適用されるので、二項分布の基礎をきちんと理解しておきましょう。

母不適合品率の検定
検定統計量
母不適合品率の確率分布は、標準正規分布$N(0,1)$に従います。
標準正規分布とは、正規分布を標準化したもので、標本平均から母平均を差し引いて中心値をゼロに補正し、さらに標準偏差で割って単位を無次元化する処理のことを表します。
詳しくは別の記事で紹介していますので、合わせてご覧ください。

標準正規分布では、分布の横軸($Z$値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのNORM.S.DIST関数や標準正規分布表で簡単に求められます。
そして、母不適合品率の検定では、この$Z$値を検定統計量として用います。
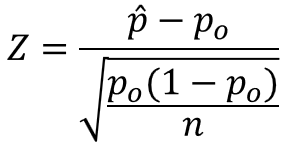
計数値と計量値の違い
実は、母不適合品率の検定は、統計的検定(その弐)で紹介した母平均の検定と基本的に同じ考え方を用いています。
その弐で紹介したものは、確率変数が正規分布やt分布に従う「計量値」でしたが、これが二項分布に従う「計数値」に置き換わっただけのことです。
二項分布は不良数$x$に関する確率分布を表したもので、期待値$E(X)=np$、分散$V(X)=np(1-p)$となります(導出過程は二項分布の記事で解説しています)。
これを不適合品率に変換する、すなわちサンプルサイズ$n$で割ると、$E(X)=p$、$V(X)=p(1-p)$となります。
母不適合品率を$p_{o}$と置くと、$E(X)=p_{o}$、$V(X)=p_{o}(1-p_{o})$となります。
ここで先ほどの検定統計量の定義の式を見てみると、分母は$\sqrt{V(X)/n}$、分子は「標本平均-母平均」になっており、母平均の検定と同じ構造の式であることが分かります。
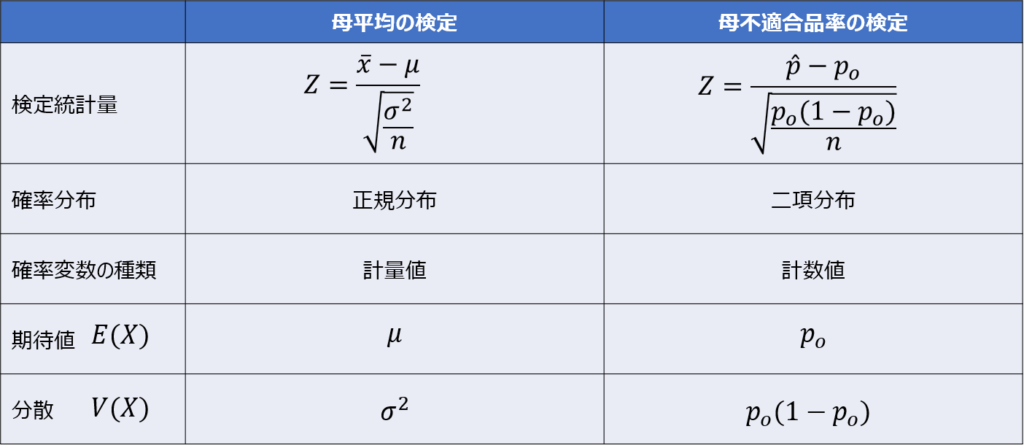
変数がたくさん登場して覚えにくい場合には、式の構造から理解しておくことをおススメします。
なお、ここまで説明した母不適合品率の検定は、区間推定と基本的に同じ考え方を用いています。
内容も重複する部分が多いですが、区間推定では信頼区間の幅を計算する際に、母不適合品率を標本不適合品率に置き換える手順を取ります。
考え方の詳細は以下の記事で紹介していますので、合わせてご覧ください。

検定の手順
それでは、実際に母不適合品率の検定をやってみましょう。
とある製品の従来からの母不適合品率は$p_{o}=0.03$であった。最近、製品の性能向上を狙いとして新しい材料に変更したところ、200個抜き取ったサンプルの不良数は10個であった。変更前と比べて不良率が増加したと言えるでしょうか?
1.仮説を設定する
まずは、検証したい目的に合致した帰無仮説$H_{0}$と対立仮説$H_{1}$を設定します。
変更後の不良率が高くなったことを背理法で証明したいので、帰無仮説を「$H_{0}:p=p_{o}$」、すなわち「変更前後の不良率に違いがない」と設定します。
また、対立仮説は本来の目的である証明したい仮説として、「変更後の不良率の方が高い」とします。
$H_{0}:p=p_{o}$
$H_{1}:p>p_{o}$(片側検定)
2.検定統計量を算出する
定義の数式に従い、検定統計量$Z$を求めます。
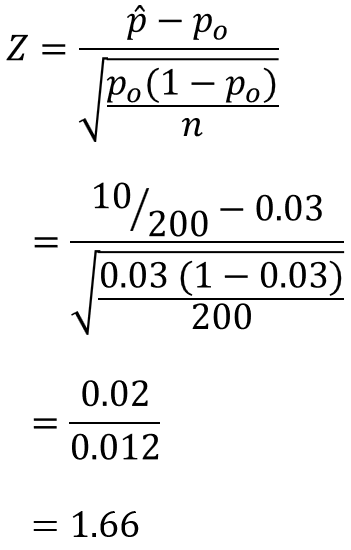
3.帰無仮説の棄却/採択を判定する
検定統計量の値から帰無仮説の棄却/採択を判定します。
判定の指標には、標準正規分布の$Z$値を用います。
通常、統計的検定では、有意水準$α=0.05$や$α=0.01$を基準として用います。
つまり、本当は帰無仮説が正しいのに、誤って棄却してしまう確率が$α=0.05$の場合は5%、$α=0.01$なら1%となる状態のことです。
標準正規分布表から確率$p=0.05$及び$p=0.01$となる$Z$値を求めると以下のようになります。
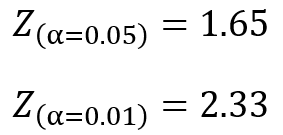

両側検定の棄却域はα/2となるから注意しよう
エクセルの場合、標準正規分布の累積分布関数の逆関数を表すNORM.S.INV関数を使えば、以下のように求めることもできます。

累積分布関数とは、以下のように$-∞$から$Z(α)$の範囲の積分値を表すので、$Z(0.05)$を求めたい場合には、確率に$0.95$を入力します。
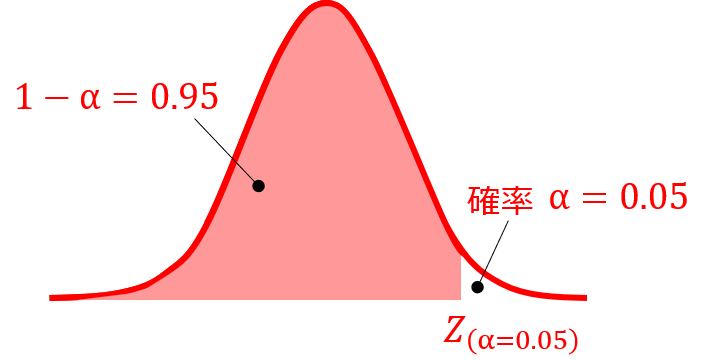
先ほどの検定統計量と比較すると、以下の関係であることが分かります。
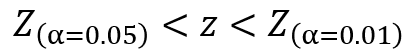
1%の棄却域には入っていないが、5%の棄却域には入っている状態、つまり有意水準5%で帰無仮説が棄却され、対立仮説が採択されるという結果となります。
4.検定の結論を導く
「有意水準5%で変更後の不良率が高くなったと言える」となります。
まとめ
- 1つの母不適合品率に関する検定統計量
⇒標準正規分布の$Z$値を用いる - 検定の手順
⇒仮説を設定する
検定統計量を算出する
帰無仮説の棄却/採択を判定する
検定の結論を導く
最後まで読んでいただき、ありがとうございました。




コメント