「正規分布ってどのような分布なの?」
「期待値と分散の計算の仕方を知りたい」
「エクセルでグラフ化したい」
このような疑問や悩みをお持ちの方に向けた記事です。
正規分布とは、分布の中央に位置する平均値において最も高い頻度を持つ、左右対称の形状が特徴の連続型の確率分布です。
例えば、身長や質量、テストの点数など、自然現象や社会現象の多くが当てはまる確率分布で、ガウス分布とも呼ばれています。
この記事では、正規分布の定義、期待値と分散の導出の仕方、エクセルでグラフ化する手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
正規分布とは?

左右対称のきれいな分布ってイメージだけど
確率密度関数を表すと以下のようになります。
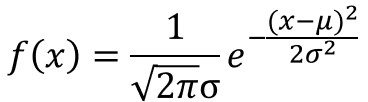
eはネイピア数(自然対数の底)、μは平均値、σは標準偏差を表し、「平均値μ、分散σ2の正規分布に従う」「X~N(μ,σ2)」と表現されます。
正規分布における確率変数Xは、連続的な値を取る計量値です。
このような連続型の確率分布における発生のしやすさを表した関数のことを確率密度関数と呼び、f(x)として表されます。
連続型確率分布や確率密度関数ついては、別の記事で詳しく解説していますので、合わせて参考にしていただければと思います。

期待値と分散の導出
正規分布における期待値E(X)と分散V(X)は、以下の数式で求めることができます。
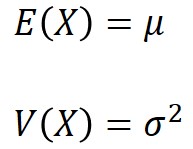
元々、正規分布とは平均値μ、分散σ2で定義される分布ですので、期待値と分散も定義の通りの値となっています。
少し難しいですが、導出過程に興味のある方は参考にどうぞ。




計算の仕方は覚えなくても大丈夫だよ
エクセルでのグラフの書き方
エクセルでの正規分布の確率の求め方、グラフの書き方を紹介します。
エクセルのNORM.DIST関数を用いれば、これ一つで確率密度関数を計算することができます。
DISTというのは、分布(distribution)の略で、NORMはnormalの略で、これを繋げた名前が関数名になっています。
使い方は簡単で、次の4つの変数を指定するだけです。
①:確率変数(x)
②:平均(μ)
③:標準偏差(σ)
④:関数形式(TRUE or FALSE)
④の関数形式については、確率密度関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
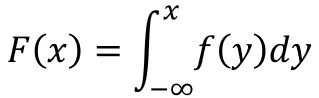
例えば、平均値μ=50、標準偏差σ=10として、確率密度関数を求めると以下のようになります。
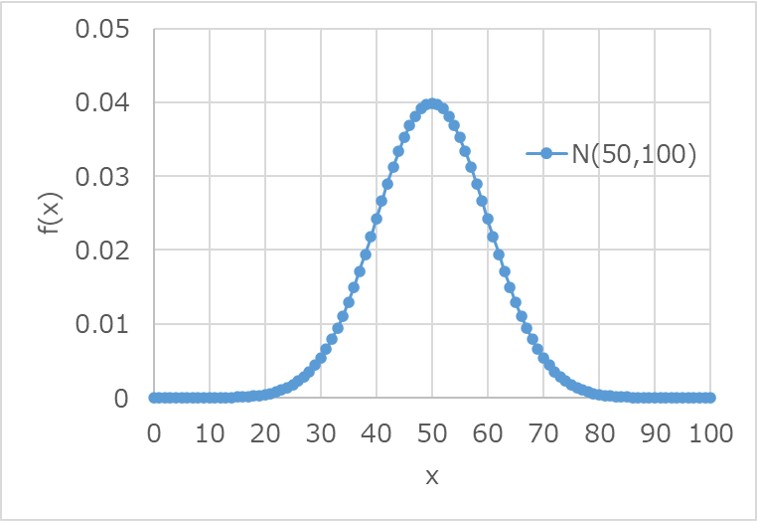
同様に累積分布関数F(x)を求めると以下になります。
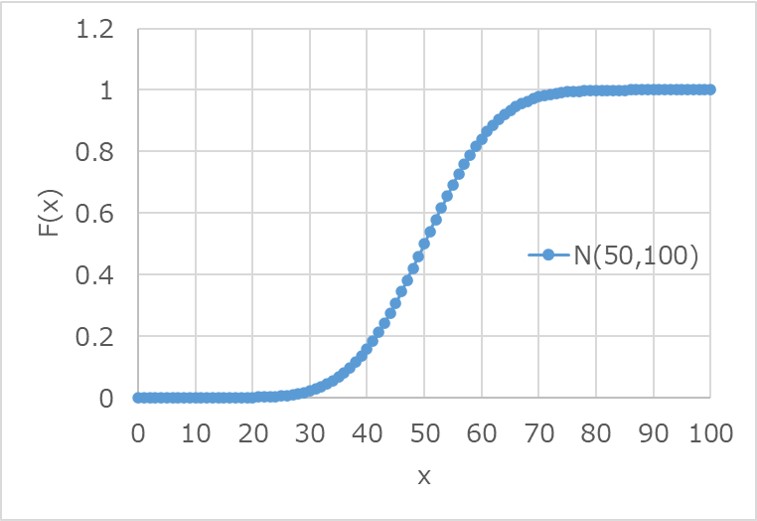
累積分布関数は、確率変数xの値が大きくなるにつれて、1に収束することが見て取れます。
これは、確率の合計値が1になることを表しており、この性質がグラフからも分かります。
偏差値の概念
ちなみに、今回の事例で紹介したμ=50、σ=10というのは、学生の頃から馴染み深い「偏差値」の分布を表しています。
テストの点数の分布において、平均点が50点、標準偏差が10点の分布になるように換算したものが偏差値で、以下の計算式で求めることができます。
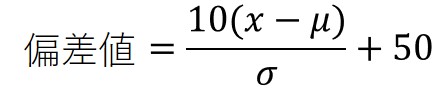
xには自分の得点を入れると、あとは平均値と標準偏差から簡単に偏差値を計算できます。
偏差値60は平均点+σ(10点)、偏差値70は平均点+2σ(20点)を表します。
なぜ偏差値の概念が用いられるのかというと、そのテストにおいて上位何%に入っているのかを客観的に表すことができるからです。
毎回、テストごとに平均点やばらつき(分散)は異なります。
そうすると、例えば同じ80点の点数でも、平均点が50点なのか、70点なのか、全体の分布しだいで良し悪しの基準が変わってきます。
これでは、成績を客観的に評価できないので、常に同じ基準で成績を図る指標として偏差値の概念が用いられるのです。
確率分布の定義として、±1σの範囲に収まる確率は68%、±2σは95.4%、±3σは99.7%と決まっています。
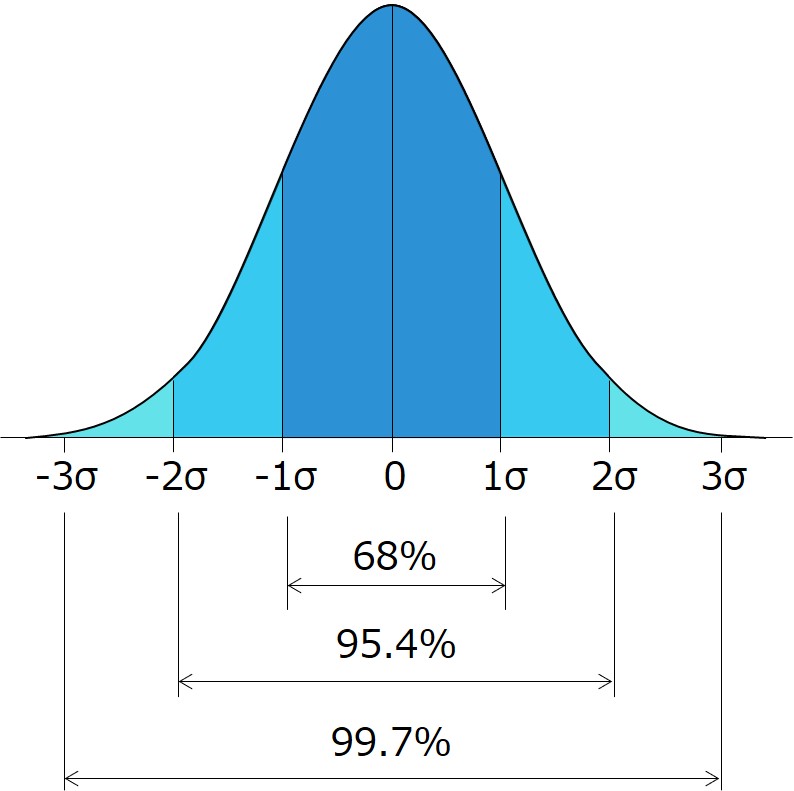
つまり、偏差値70以上というのは、平均値+2σ以上を意味しており、上位2.3%であることを表しています。
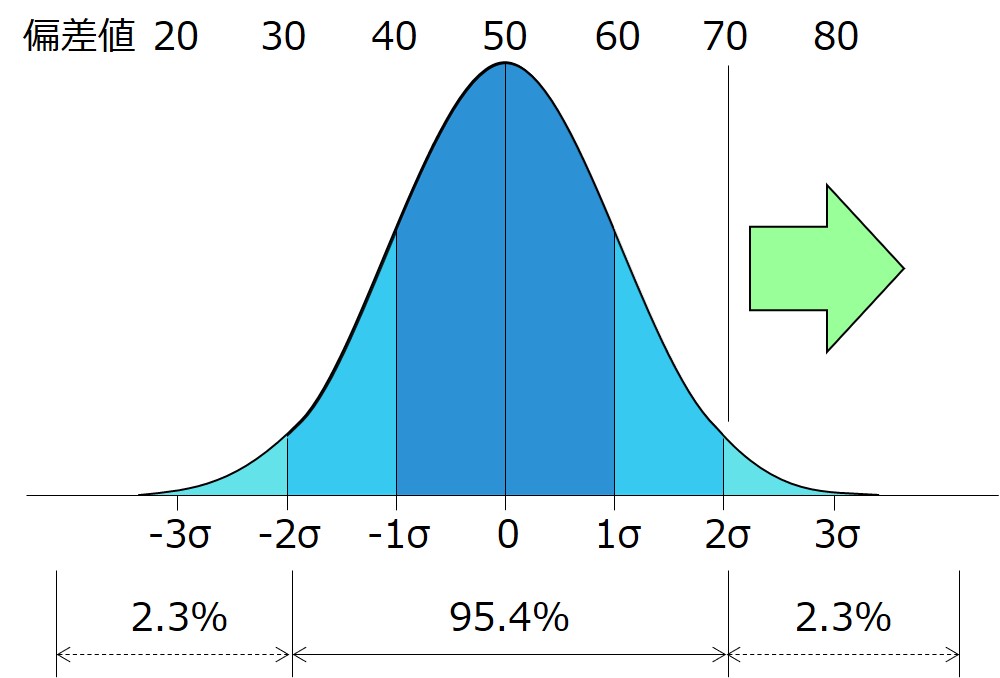
このように表現すれば、偏差値70がどの程度優秀なのか、ひと目で分かるので便利ですね。

標準正規分布とは?
標準正規分布とは、正規分布の平均値を0、標準偏差を1に換算した分布のことで、N(0,1)と表されます。
通常の正規分布では、単位やデータ範囲がそれぞれ異なり、データ間での分布の単純比較ができません。
また、データ範囲△△~○○に収まる確率を求めようとした場合、エクセルなどで累積分布関数を計算できれば良いですが、手元に計算ツールがないと困ります。
このような場合に、あらかじめ分布のデータの単位を無次元化し、データのばらつきの範囲を揃えることで、上記の問題を解消することができます。
正規分布を標準化することで、「標準正規分布表」を読み取るだけで所望の範囲の確率を求めることができるのです。
標準正規分布表の読み方
以下に、標準正規分布表を示します。
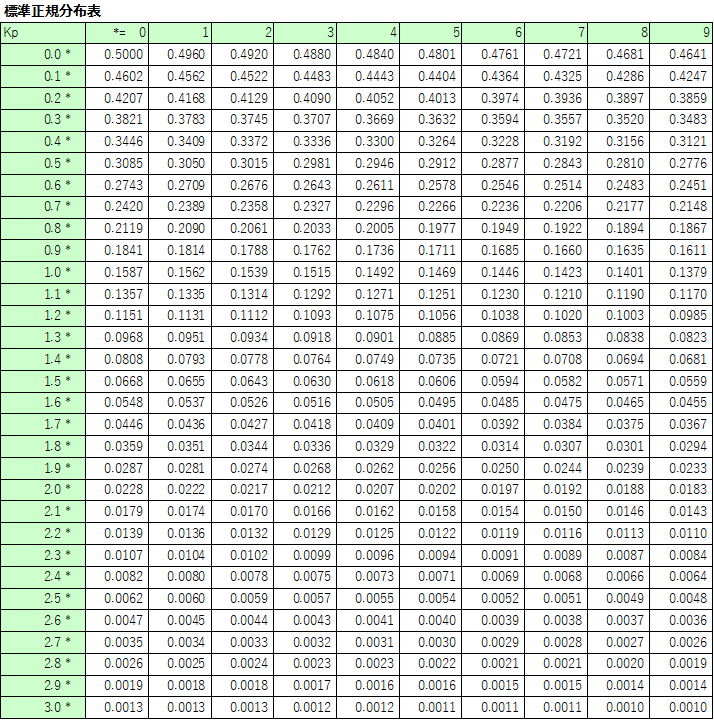
Kpは、確率変数の値を表します。
そして、Kpの値に対し、小数点一桁までを縦軸、二桁目を横軸に表し、マトリックスの交差する箇所に対応する確率が記載されています。
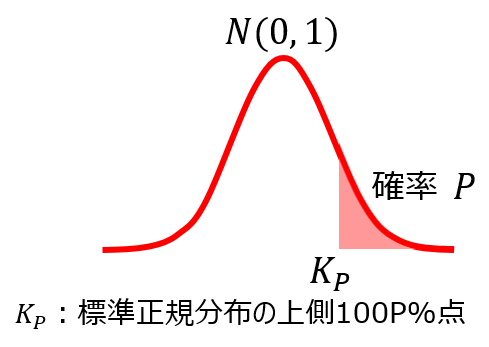
ここで示す確率は、とあるKp値よりも分布の右側にあたる確率、つまり上側確率としてPに示す部分の確率を表しています。
Kp値のマイナス側がないのは左右対称のため、省略されています。
例えば、Kp=1.00の場合、1.0と0.00の交差するセルの値は、0.1587と読み取れます。
つまり、Kpが1以上の範囲に15.87%が収まることを意味しています。
ちなみに、Kpが-1以下の確率も、これと同様に15.87%となります。
逆に言うと、Kpが-1~1の間に収まる確率は、全体の100%から左右の15.87%ずつ(31.74%)を引いた値になるので68.26%となり、先ほどの偏差値の項目で説明した、±1σに収まる確率が68%という値と合致していることが分かりますね。
このように、標準正規分布表を読み取ることで、複雑な計算をしなくても、所望の範囲の確率を簡単に求められるのです。

標準化のひと手間で、あとの計算が楽になるんだね
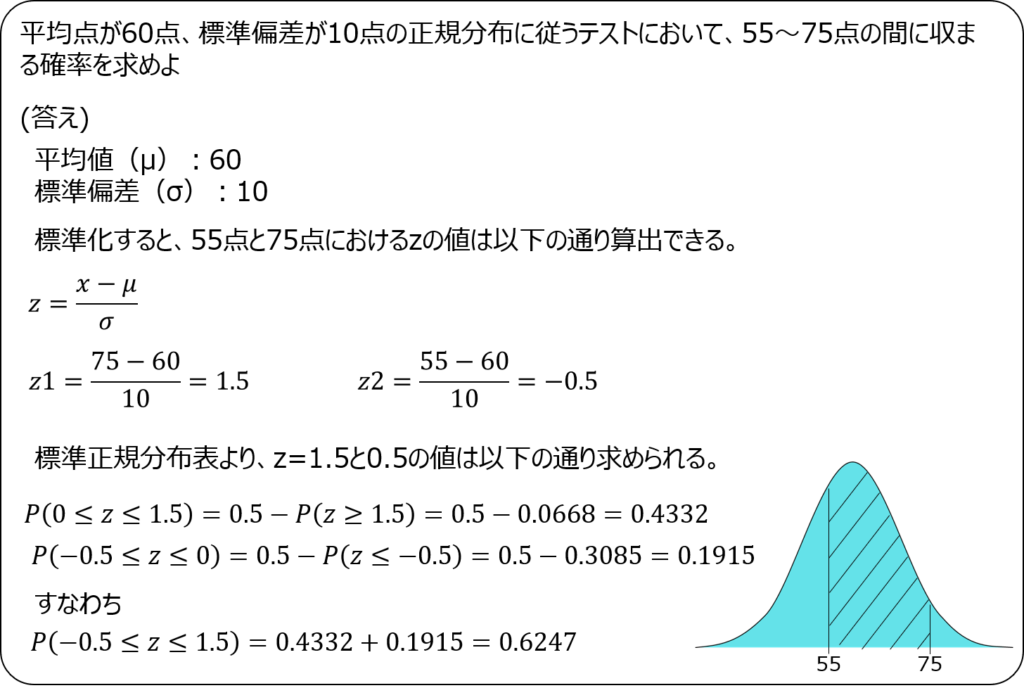
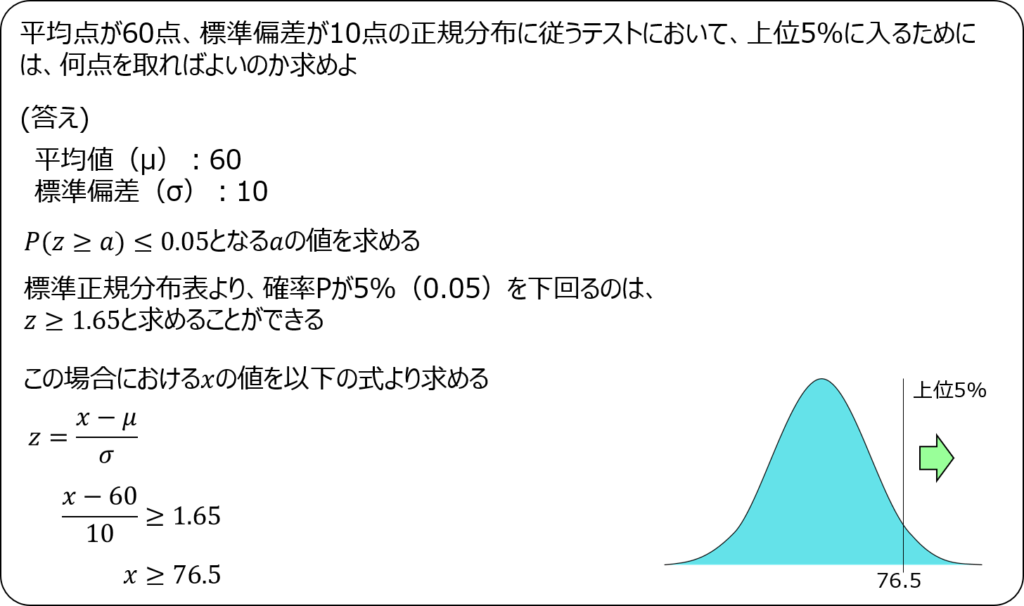
例題
まとめ
- 正規分布
⇒分布の中央に位置する平均値において最も高い頻度を持つ、左右対称の形状が特徴の連続型の確率分布のこと - 期待値
⇒μ(平均値) - 分散
⇒σ2 - エクセルでの求め方
⇒NORM.DIST関数で、確率密度関数と累積分布関数を計算できる - 標準正規分布
⇒正規分布の平均値を0、標準偏差を1に換算した分布のこと
⇒標準正規分布表を読み取るだけで、所望の範囲に収まる確率を算出できる
正規分布が当てはまる身近な事象も多いので、ぜひ一度エクセルを使って計算してみてください。
最後まで読んでいただき、ありがとうございました。
この記事で紹介した正規分布は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。





コメント