「確率密度関数ってどういう意味?」
「どのような活用の用途があるの?」
「期待値と分散の計算の仕方を知りたい」
こんな疑問や悩みをお持ちの方に向けた記事です。
確率密度関数とは、確率変数が連続的な値を取る分布において、発生のしやすさを関数に表したものです。
この記事では、確率密度関数の定義、活用の用途、期待値と分散の計算の仕方について、初心者の方にもわかるよう例題を用いて基本から解説しています。
正規分布や二項分布などの基礎となる考え方ですので、これから統計学の勉強を始めようという方にとって、参考になればうれしいです。
確率密度関数の定義
確率変数とその発生確率の対応を表した確率分布には、離散型と連続型の2種類があります。
離散型とは確率変数が不連続な値を取る分布のことで、二項分布やポアソン分布といったように計数値を変数とすることが特徴です。
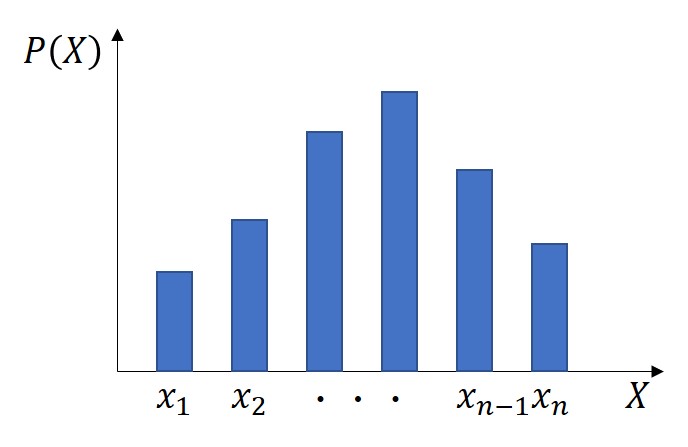
例えば、サイコロの6つの目のように、変数が6通りと決まっており、それぞれの目に対して発生確率が1/6といったように、確率との対応が付いています。
一方、連続型とは確率変数が連続的な値を取る分布のことで、正規分布や指数分布といった計量値を変数とすることが特徴です。
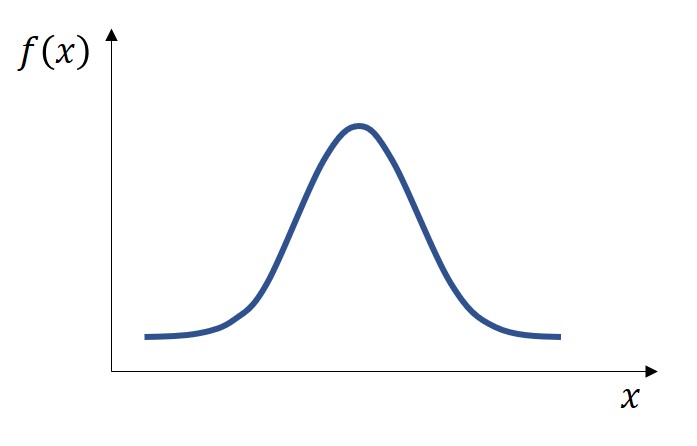
連続型の場合、例えば長さや質量のように変数の値が連続的に変化するので、とある一点の変数xにおける確率P(x)を求めることはできません。
例えば、長さを確率変数として、ジャスト1mの発生確率を求めることを想像してみてください。
0.999や1.001などを別の値とすると小数点以下は無限に分解され、ピンポイントの点での確率が出せないのは感覚的にも分かっていただけると思います。
ところが、例えば0.999~1.001mの範囲に入る確率であれば求めることが可能です。
確率密度関数は、連続型確率分布において発生のしやすさを関数に表したもので、とある範囲に収まる確率を求めるために用いられます。
確率密度関数f(x)と確率P(X)の関係性を数式と模式図で表すと、以下のようになります。
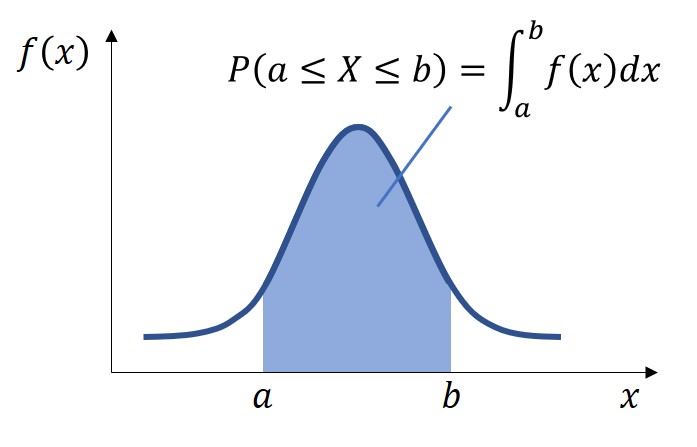
つまり、確率密度関数の積分値として面積を求めることで、その範囲内の発生確率を算出できるのです。

「面積=確率」の考え方は、検定や推定でも使うから覚えておこう
ここまで、確率変数や確率分布などの用語が登場しましたが、別の記事で詳しく解説していますので、合わせて参考にしていただければと思います。

確率密度関数の性質
以下の3つの性質があります。
1.必ず0以上の値となる
発生のしやすさを表す関数なので、マイナスの値をとることはありません。
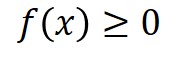
また、確率と混同しがちですが、そもそも次元が異なるもので、1より大きい値を取ることもあります。
2.定積分の値が確率を表す
定義のところでも説明した通り、定積分の値(面積)が、その範囲における発生確率を表しています。
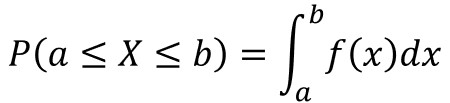
3.全範囲の積分値は1となる
面積が確率を表すということは、全範囲の面積は、確率の合計値になるので必ず1となります。
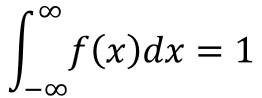
離散型確率分布の場合、例えばサイコロの1~6のどれかが出る確率が1(100%)というのは、直感的に理解できると思います。
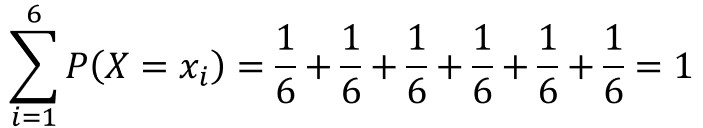
連続型確率分布も同じで、全範囲として-∞から+∞を指定すると、必ず面積は1となるということです。
累積分布関数とは
確率変数がある値以下となる確率の関数のことで、大文字のF(x)を用いて以下の数式で定義されます。

連続型確率分布の数式で確率密度関数をf(y)としているのは、積分範囲としてのxと確率密度関数の変数が紛らわしくならないように、別の文字で置き換えて記載しています。
累積分布関数は、確率密度関数の積分で、つまり確率を表す関数となります。
そのため、例えば、aからbの範囲の確率を求める場合には、以下の計算式で求めることができます。
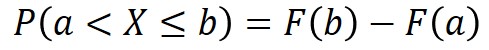
累積分布関数のイメージを図示すると以下となります。確率の合計値として、xが∞の場合に1に収束します。
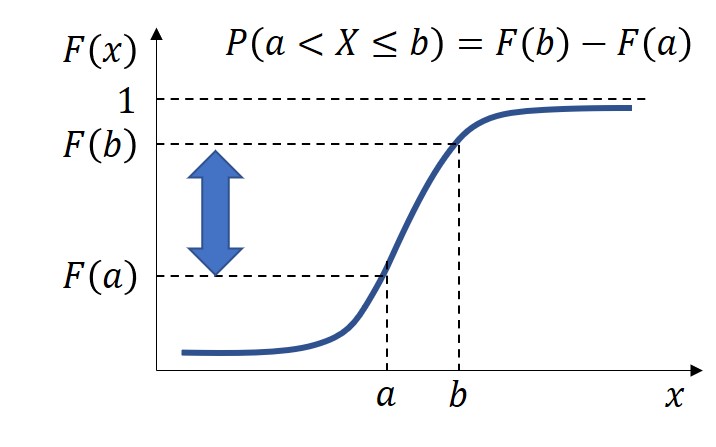
ちなみに、aの不等号にイコールが入っていないのは、F(x)が「ある値以下」となる確率として定義され、つまり上式には確率変数X=aが含まれないことを意味します。
ただし、確率密度関数の性質でも説明した通り、とある一点での確率は存在しないので、表記だけの問題で計算結果には何も影響しません。
確率変数の期待値と分散
期待値というと宝くじやギャンブルのイメージに繋がるかもしれませんが、確率分布を取り扱う上では最も基本的な要素の一つです。
とある標本調査において、母集団の傾向を掴むのに個々のデータから平均値やばらつき(分散)を求めるのと同じく、確率の世界においても分布の傾向を表す指標があります。
その一つ目が期待値で、発生確率を考慮した確率変数の平均値を意味し、以下の数式で表されます。

また、分布の傾向を表す二つ目の指標として、分散があります。
これは、個々のデータの分散を求める場合と同じで、平均値との差分の二乗和で求めることができます。
以下の式で、mは期待値E(X)を表します。

上式は計算が複雑なので、以下のように変形すると計算が簡単になります。

この関係性は、離散型確率分布においても同じなので、期待値の関数E(X)が分かれば、分散V(X)を簡単に求めることができます。

すごくシンプルな計算式になるんだね
例題
①:確率密度関数
②:期待値と分散

まとめ
- 確率密度関数
⇒確率変数が連続的な値を取る分布において、発生のしやすさを関数に表したもの
⇒積分した面積の値が確率を意味する - 確率密度関数の性質
⇒必ず0以上の値となる
定積分の値が確率を表す
全範囲の積分値は1となる - 累積分布関数
⇒確率変数がある値以下となる確率の関数 - 確率変数の期待値
⇒発生確率を考慮した確率変数の平均値 - 確率変数の分散
⇒ばらつきを意味し、平均値との差分の二乗和で算出
定積分と確率の関係性は、統計学を知る上で切り離せない重要ポイントなので、ぜひ基本的な考え方をおさえておきましょう。






コメント