「二項分布ってどのような分布なの?」
「期待値と分散の計算の仕方を知りたい」
「エクセルでグラフ化したい」
このような疑問や悩みをお持ちの方に向けた記事です。
二項分布とは、成功か失敗のいずれかとなる試行において、成功回数を確率変数とした離散型の確率分布を表します。
コイン投げで表が出る回数や、勝率○○%で当たりを引く回数など、一度は身近な例を聞いたことのある方も多いかもしれません。
この記事では、二項分布の定義、期待値と分散の導出の仕方、エクセルでグラフ化する手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
二項分布とは?
成功か失敗のいずれかで表される試行のことをベルヌーイ試行と呼びます。
ベルヌーイ試行を1回行う場合において、成功する確率を$p$とすると、失敗する確率は$1-p$となります。
そして、これを何回も繰り返した場合における成功回数の分布を二項分布と呼び、以下の数式で定義されます。
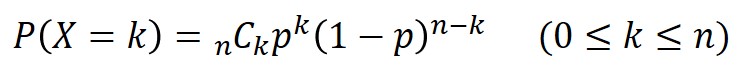
$n$は試行回数、$p$は成功確率、$k$は成功回数を表し、「確率変数$X$は二項分布$B(n,p)$に従う」と表現されます。

nCkは、成功が何回目に出るかの通り数ってことだね
二項分布における確率変数$X$は、成功回数$k$であり、1回、2回・・と数えることのできる計数値です。
そのため、例えば1から2の間の小数点以下の変数は取らない、離散的な変化をする性質の確率分布となっています。
このような離散型の確率分布が示す確率のことを確率質量関数と呼び、$P(X=k)$として表されます。
離散型確率分布や確率質量変数ついては、別の記事で詳しく解説していますので、合わせて参考にしていただければと思います。

期待値と分散の導出
二項分布における期待値$E(X)$と分散$V(X)$は、以下の数式で求めることができます。
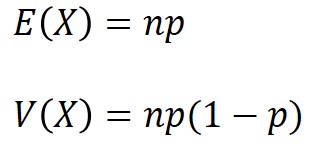
試行回数$n$と成功確率$p$のとても簡単な計算ですが、その導出の過程は以下の計算手順を経ています。
少し難しいですが、導出過程に興味のある方は参考にどうぞ。



なお、$E(X)$と$V(X)$の意味、$V(X)$と$E(X)$の関係式の導出過程については、別の記事で解説していますので、合わせてご覧ください。

エクセルでのグラフの書き方
エクセルでの二項分布の確率の求め方、グラフの書き方を紹介します。
エクセルには便利な関数があり、BINOM.DIST関数を用いれば、これ一つで確率質量関数を計算することができます。
どこで切って、何と読めば良いのか分かりにくいですが、二項分布の英語であるバイノミナル・ディストリビューション(binomial distribution)の略称と覚えておきましょう。
使い方は簡単で、次の4つの変数を指定するだけです。
①:成功数($k$)
②:試行回数($n$)
③:成功率($p$)
④:関数形式(TRUE or FALSE)
④の関数形式については、確率質量関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
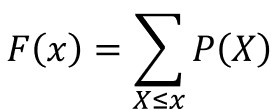
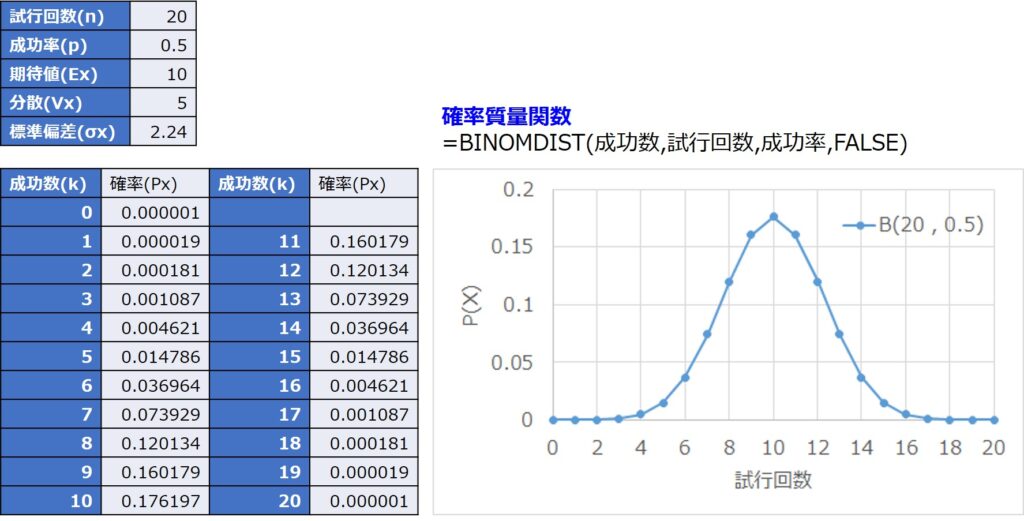
例えば、$n=20$、$p=0.5$として、確率変数$X=k$における確率質量関数$P(X)$を求めると以下のようになります。
また、同様に確率変数$X=k$における累積分布関数$F(X)$を求めると以下になります。
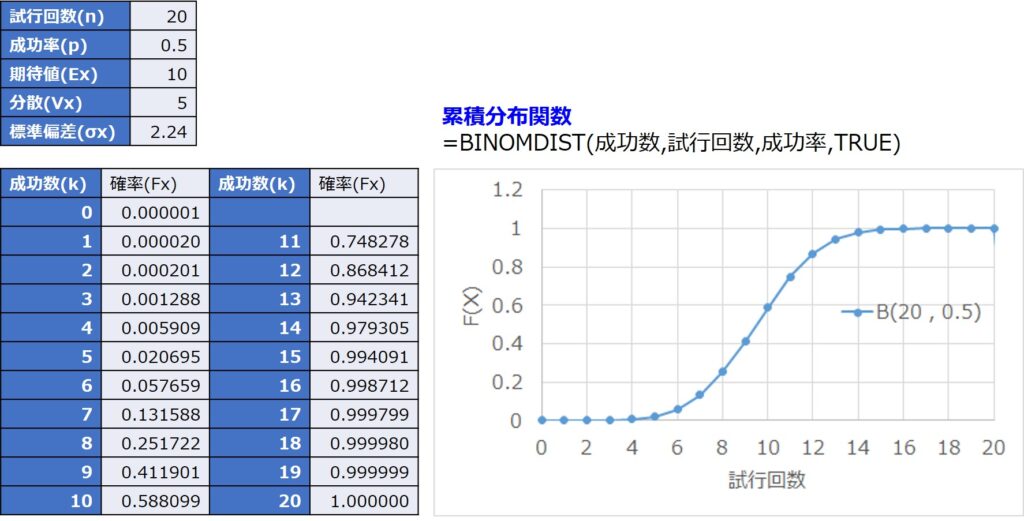
成功回数20回における累積分布関数は、0回から20回の全範囲の合計値となるので、1となることがグラフからも見て取れます。

エクセルだと関数ひとつで済むんだ
試行回数の違いによる影響
試行回数の違いによって、分布形状がどのように変化するのか見てみましょう。
以下は、成功率$p$を$0.5$で固定した場合における、$n=10$、$20$、$40$の二項分布です。
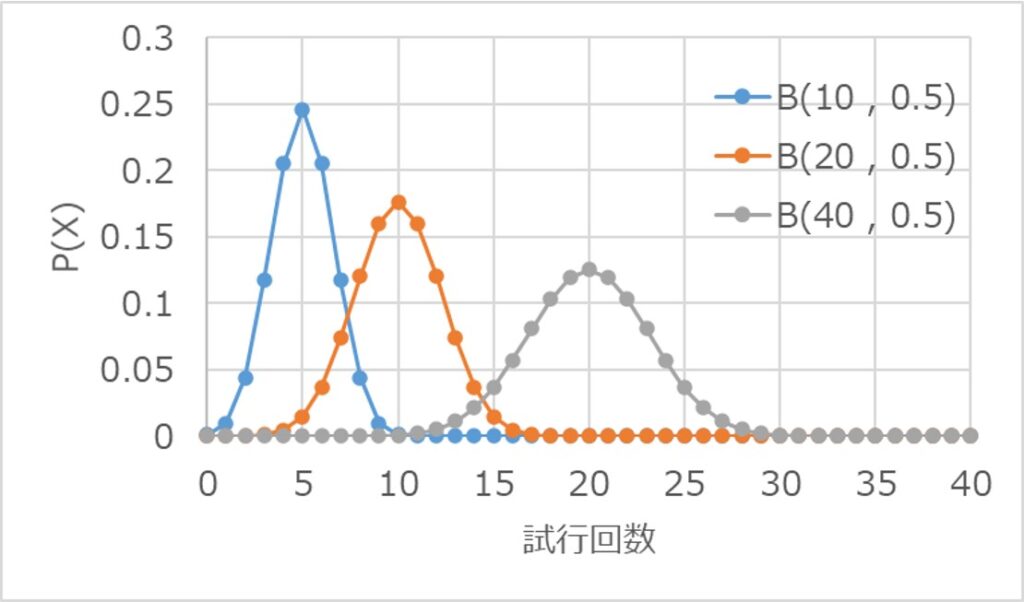
試行回数の大小によらず、期待値(平均値=$np$)付近の確率が最も高く、中心から離れるにつれて下がっていく傾向が見られます。
分布の形状としては、$n=10$の場合は、やや不連続なカーブですが、$n=40$になると非常に滑らかな曲線に近づいていることがわかります。
そして、二項分布の重要な性質として、「$np$の値が十分に大きい場合には、正規分布として近似できる」という特徴を覚えておきましょう。
一般的には、$np>5$が一つの目安とされており、以下のように両者の分布がほとんど合致することが分かります。
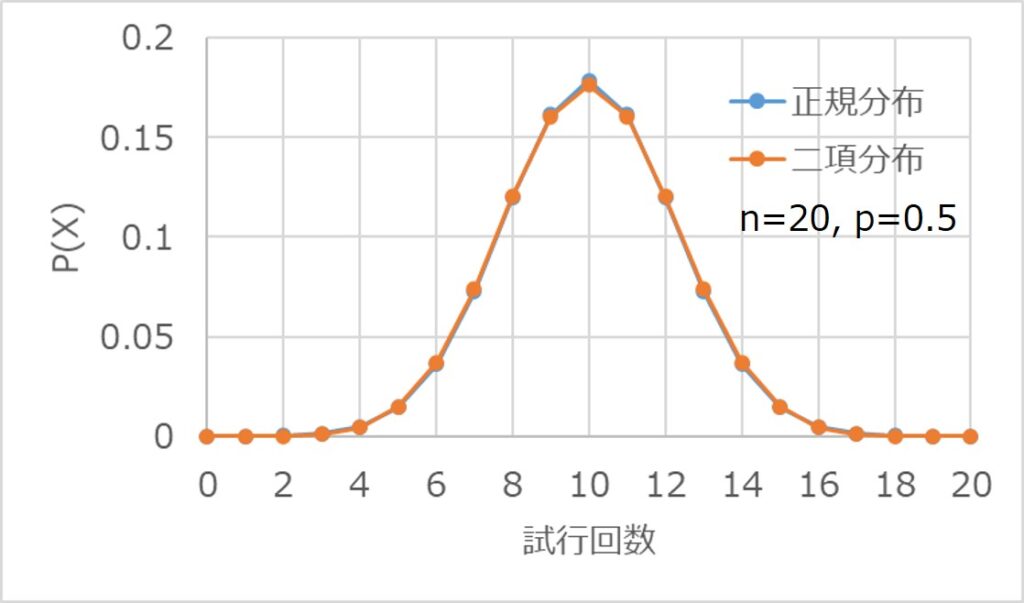
なお、$p$が偏って高い場合も考えられるので、失敗の期待値$n(1-p)$と合わせて、どちらも5より大きいことを目安に考えましょう。
正規分布に近似するメリット
それでは、なぜ二項分布を正規分布に近似して考える必要があるのか、メリットを説明しておきます。
正規分布には、「標準正規分布表」と呼ばれる便利な表が存在します。
標準正規分布表を用いれば、マトリックスの交差する値を読み取るだけで、とある確率変数の範囲に入る確率を求めることができます。
そして標準正規分布は、正規分布の確率密度関数から平均値と標準偏差(分散の平方根)を用いれば、簡単に変換することができます。
つまり、二項分布を正規分布として近似できれば、とある範囲内の確率を瞬時に見積もることができるのです。

複雑な計算式も不要で簡単に求められるんだね
例題

まとめ
- 二項分布
⇒成功か失敗のいずれかとなるベルヌーイ試行を複数回繰り返した場合において、成功回数を確率変数とした離散型の確率分布のこと
⇒コイン投げで表が出る回数、勝率○○%で当たりを引く回数など - 期待値
⇒$np$(=試行回数×成功率) - 分散
⇒$np(1-p)$(=試行回数×成功率×(1-成功率)) - エクセルでの求め方
⇒BINOM.DIST関数で、確率質量関数と累積分布関数を計算できる - 二項分布の特徴
⇒$np$が十分に大きい場合には、正規分布として近似できる
累乗の計算もエクセルを用いれば、あっという間に求めることができます。
数式の複雑さに敬遠せずに、ぜひ身近な題材で活用してみてください。
最後まで読んでいただき、ありがとうございました。
この記事で紹介した二項分布は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。








コメント