「t分布ってどういう分布なの?」
「どのような使い道があるの?」
「エクセルやt分布表で実際に確率を求めたい」
このような疑問や悩みをお持ちの方に向けた記事です。
t分布とは、母集団の標準偏差が未知の場合において、標本の標準偏差を用いて標本平均を標準化したときの値「t」が従う確率分布のことです。
統計学の上では平均値の差に関する検定や平均値の区間推定などを行う上で欠かせない基礎知識の一つです。
この記事では、t分布の定義と性質、活用の用途、期待値と分散の導出の仕方、エクセルやt分布表から確率を求める手順について解説しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
t分布とは?
定義
最初にt分布の定義を説明します。
t分布とは、母集団の分散や標準偏差が未知の場合において、以下の数式によって標本平均を標準化したときの値tが従う確率分布のことです。
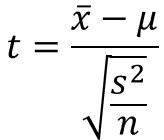
$\bar{x}$は標本平均、$μ$は母平均、$s^{2}$は不偏分散、$n$はサンプルサイズを表します。
別の表現を用いると、平均値$μ$、不偏分散$s^{2}$の正規分布に従う母集団から$n$個のサンプルを採取する際に、上記に定義されるtの値は自由度$n-1$のt分布に従う、と言います。
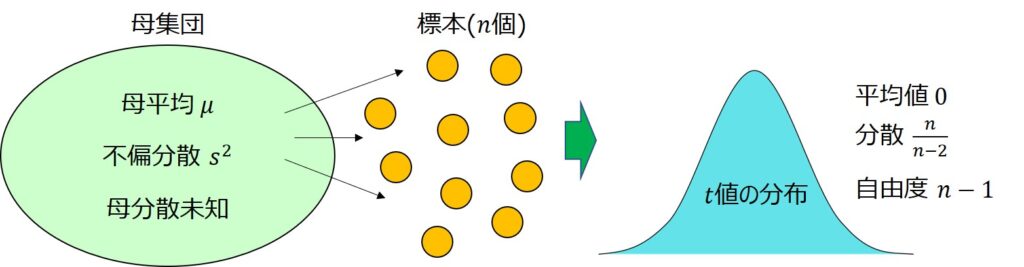
t分布は、当時ギネスビールの社員であったゴセット(William Sealy Gosset)によって初めて提唱されました。
彼がt分布に関する論文を発表する際、「Student」というペンネームを用いたことから、スチューデントのt分布とも呼ばれています。

母分散が分からない場合は、t分布を使えばいいんだね
確率密度関数
t分布の確率密度関数は以下の数式で定義されます。
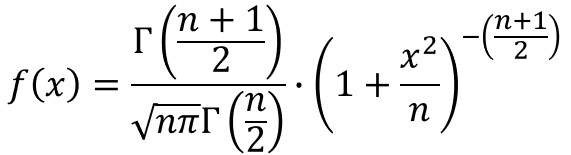
$Γ()$はガンマ関数を意味します。
ガンマ関数とは、階乗の概念を表す特殊な関数で、$Γ(n)=(n-1)!$として定義されます。
数式が非常に難解ですが安心してください、覚える必要はありません。
後ほど説明するエクセルの関数やt分布表を用いれば、複雑な計算式を解かなくても、簡単に確率を求めることができます。
なお、標準正規分布や確率密度関数については、別の記事で詳しく紹介していますので、合わせて参考にしていただければと思います。


t分布の性質
t分布に関する主な性質を紹介します。
1.標準正規分布およびカイ二乗分布との関係
標準正規分布$N(0,1)$に従う確率変数$Z$、および自由度$φ$のカイ二乗分布に従う確率変数$W$が与えられるとき、以下の数式で定義される値$t$は自由度$φ$のt分布に従います。
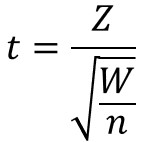
2.不偏分散とt分布の関係
以下の数式で与えられる$W$は、自由度$φ-1$のカイ二乗分布に従います。
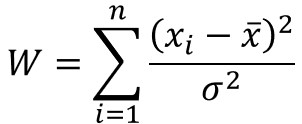
また、正規分布に従う確率変数$X$を標準化すると、以下の数式により、確率変数$Z$に変換できます。
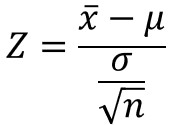
これらを先ほどの式に代入すると、以下のように変換できます。
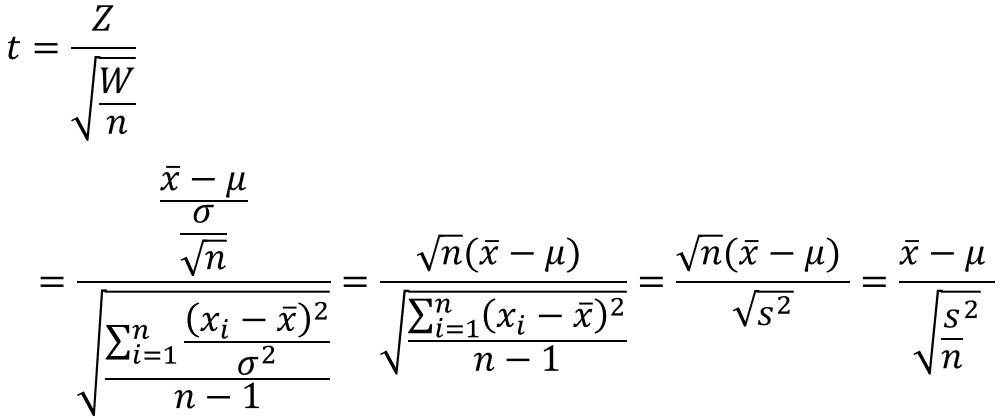
これは、最初に説明したt分布の定義と同じ式であり、すなわち、自由度$φ$のt分布に従うことが導出されるわけです。

活用の用途
1.母平均の検定と推定
母平均の検定とは、ある標本調査の結果から得られた平均値が、母平均の値と等しいか、否かを調べるための検定手法のことです。
また、母平均の推定とは、ある標本調査の結果から得られた平均値から、母平均の範囲(信頼区間)を推定する手法のことです。
どちらも平均値に関する確率として、t分布が適用されます。
2.無相関の検定
無相関の検定とは、ある標本調査から求めた相関係数に意味があるのか、否かを調べるための検定手法のことです。
「意味がある」というのは、相関係数がゼロではない、つまり何らかの関係性があることを表しています。
以下の図のように、母集団からランダムにサンプリングを何度も行い、それぞれの試行において相関係数$r$を求めます。
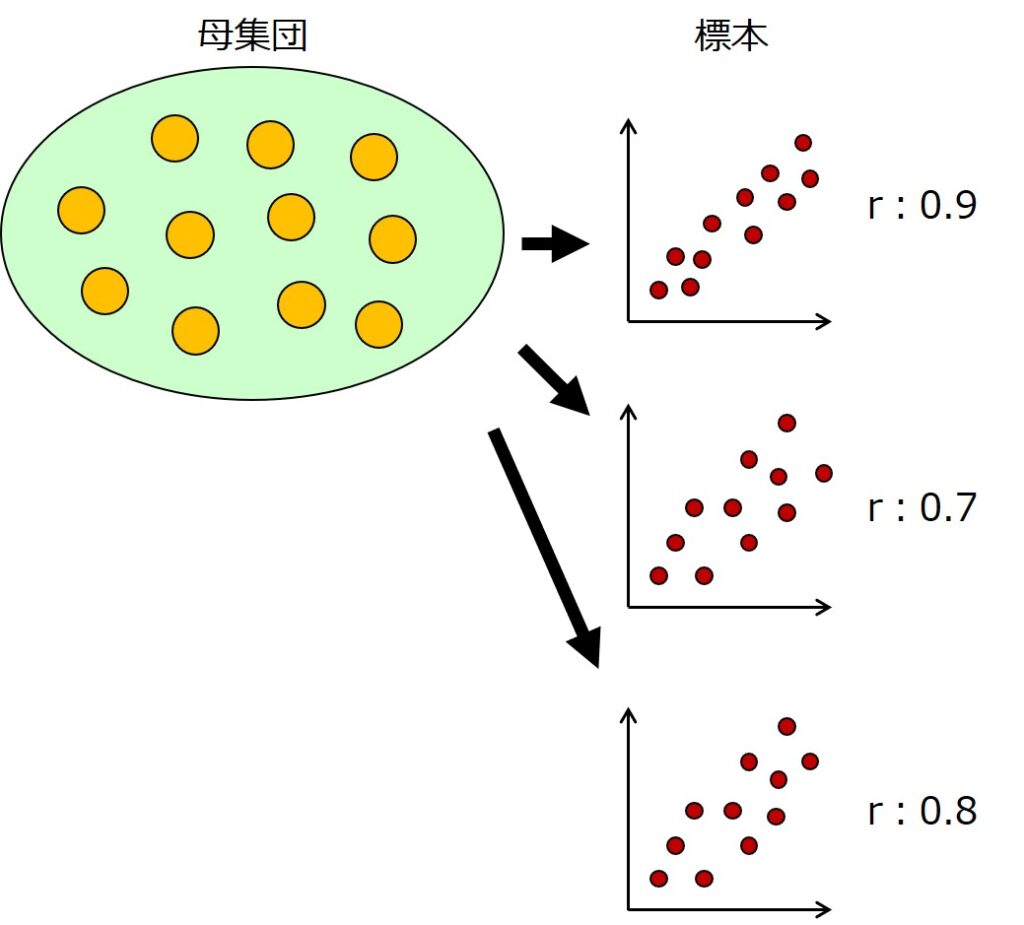
そして、相関係数$r$をもとに、以下の数式で算出される値tは、自由度$n-2$のt分布に従うことが分かっています。
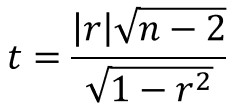
帰無仮説を「母相関係数はゼロである」とした場合に、確率的に十分に起こり得るのか、稀な事象で起こりえないものか、t分布から求めることで、相関の有無を調べられるのです。
3.回帰分析の偏回帰係数の検定
無相関の検定に近いイメージで、t分布は重回帰分析のパラメータの検定にも活用できます。
重回帰分析は、説明変数(パラメータ)が複数ある場合における目的変数との関係を多項式で表したものです。
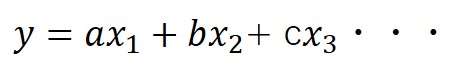
ここで、それぞれの説明変数の値に意味があるのか否か、先ほどの無相関の検定と同じ要領で、t検定を用いて統計量として調べることができるのです。

相関係数の分布も正規分布に従うってことだね
期待値と分散の導出
t分布における期待値$E(X)$と分散$V(X)$は、以下となります。
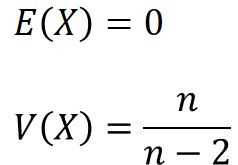
導出過程に興味のある方は参考にどうぞ。


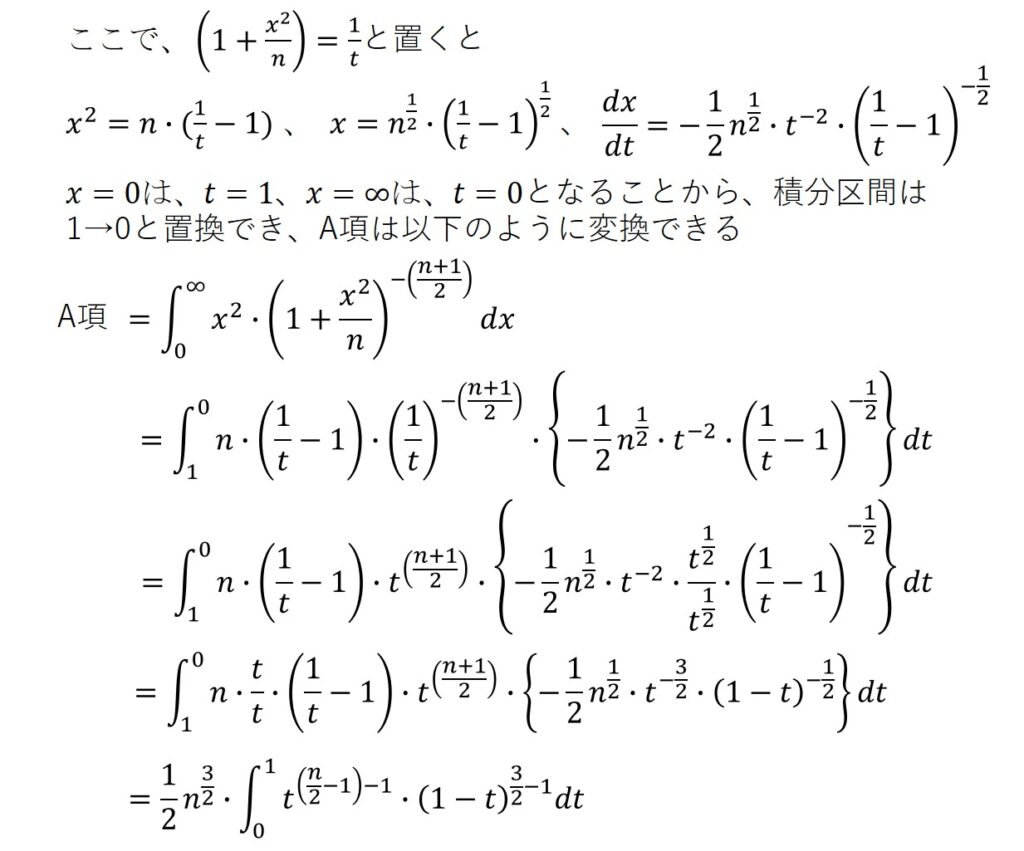

なお、$E(X)$と$V(X)$の意味、$V(X)$の導出の過程については、別の記事で解説していますので、合わせてご覧ください。

エクセルでのグラフの書き方
エクセルでのt分布の確率の求め方、グラフの書き方を紹介します。
T.DIST関数を用いれば、確率密度関数を計算することができます。
DISTというのは、分布(distribution)の略で、Tはt分布のそのままの名称で、これを繋げた名前が関数名になっています。
使い方は簡単で、次の3つの変数を指定するだけです。
①:t値
②:自由度
③:関数形式(TRUE or FALSE)
③の関数形式については、確率密度関数を求めたい場合はFALSE、累積分布関数を求めたい場合はTRUEを選択しましょう。
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
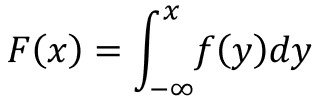
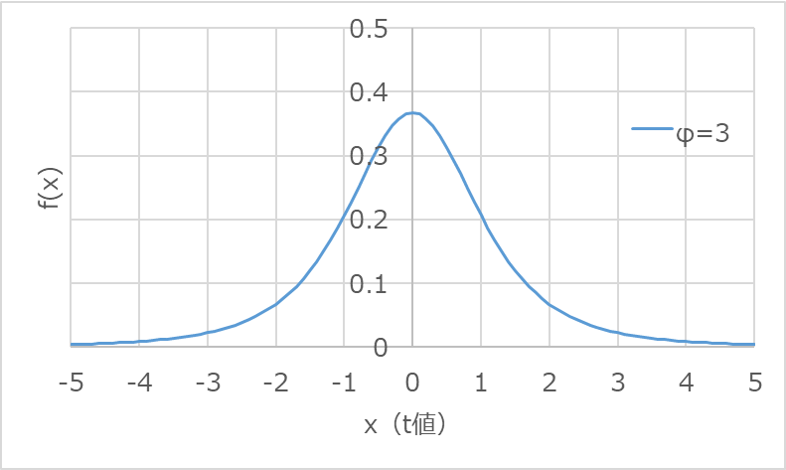
例えば、自由度3として、確率密度関数$f(x)$を求めると以下のようになります。
また、同様に累積分布関数$F(x)$を求めると以下になります。
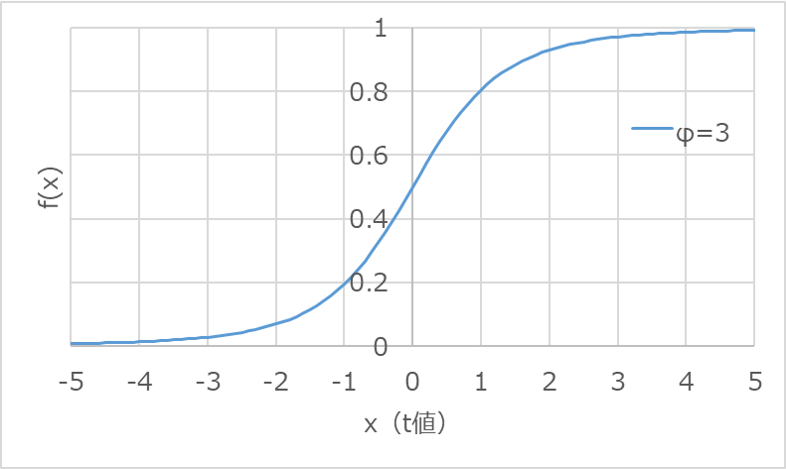
累積分布関数は、確率変数$x$の値が大きくなるにつれて、1に収束することが見て取れます。
これは、確率の合計値が1になることを表しており、この性質がグラフからも分かります。
なお、エクセルではT.DIST.RT関数やT.DIST.2T関数と呼ばれるものもあります。
累積分布関数$F(x)$は、確率変数がある値以下として定義されますが、T.DIST.RT関数はある値以上の確率を表しており、つまり、以下の数式をこの関数で直接計算できるのです。

これは、t分布を用いた検定や推定を行う際に、t値がある値以上になる確率を求める場合も多いため、関数として用意されている訳です。
また、T.DIST.2T関数は両側確率、つまりある値以下、ある値以上の範囲に入る確率を表しており、T.DIST.RT関数の2倍の値となります。

片側確率と両側確率どちらも使えるようにしておこう
t分布のグラフの特徴
左右対称の形状を示す
これまでグラフの形状を見ていただいた通り、t分布は左右対称の形状を示します。
以下のグラフは、自由度の違いによる確率密度関数の形状の違いを表したものです。
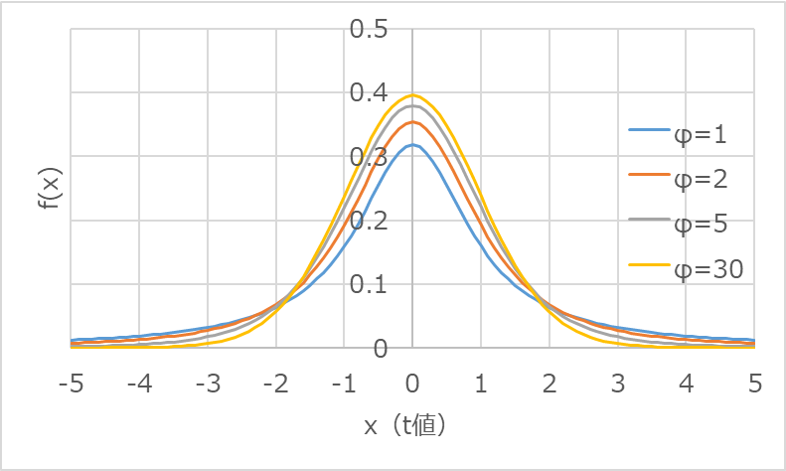
いずれも左右対称の形状ですが、自由度が大きくなるにつれて、中央のピークが高くなり、横軸のばらつきが小さくなっていきます。
横軸の分布が広いというのは、それだけ「ばらつきが多めに見込まれている」ことを意味します。
t分布では、母分散が未知の代わりに不偏分散を用いて確率を求めていますが、不偏分散そのものが母分散を推定した値であるため、すでに不確かさが含まれています。
そのため、母分散で定義される正規分布よりも、不確かさの分だけ横に広がった分布となるわけです。
無限大で正規分布に収束する
t分布の自由度を大きくして極限を取ると、標準正規分布$N(0,1)$に近似できます。
以下は、自由度φ=30におけるt分布と、標準正規分布をプロットしたグラフです。
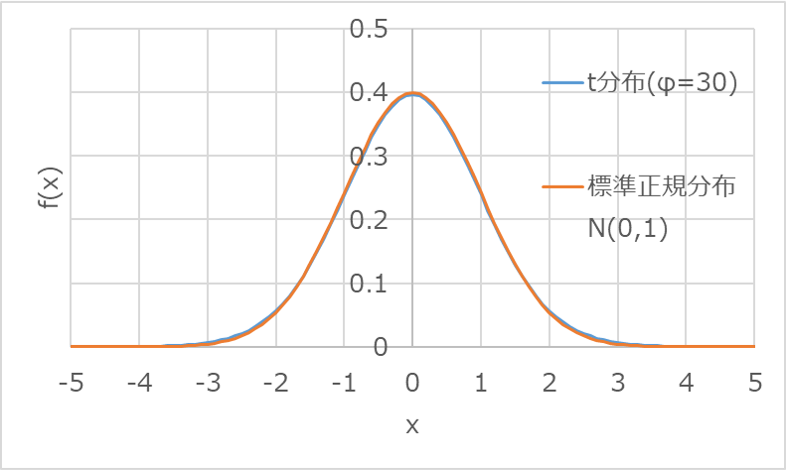
全体的な分布形状としてはほぼ一致しており、自由度が十分に大きい場合には標準正規分布として扱って問題ないことがグラフを見ても理解いただけるかと思います。
一般的に自由度が十分に大きいというのは、30以上の場合を表すことが多いです。
t分布表の読み方
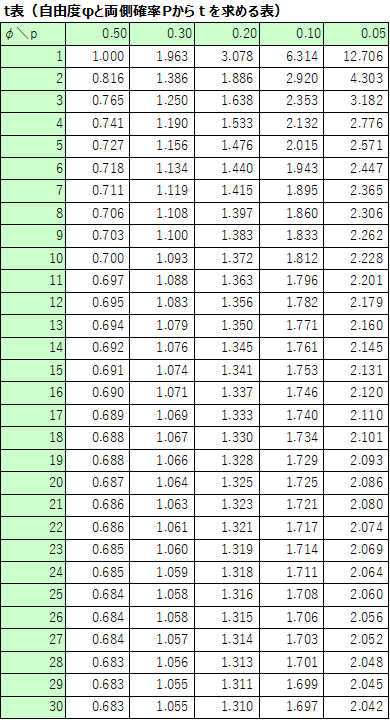
t分布表とは、横軸に確率$p$、縦軸に自由度$φ$を取って、マトリックスの交差する箇所に対応するt値が記載されている表です。
ここで表す確率$p$は、t値に対する両側確率を意味します。
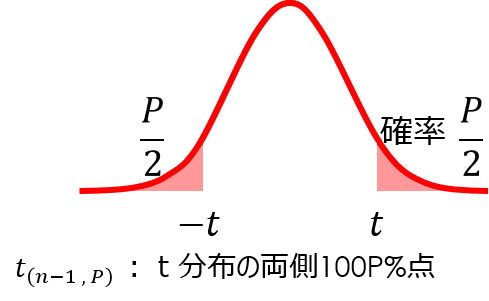
例えば、自由度$φ=5$、両側確率$p=0.1$におけるt値は$t=2.015$と読み取ることができます。
活用例の項目でも説明した各種の検定や推定を行う際に、t分布表を用いれば、複雑な計算をすることなく、所望のt値を得られるので大変便利です。
なお、エクセルを用いて自分でt分布表を作る場合は、T.INV.2T関数を用いると簡単に計算することができます。
これは、t分布の確率の両側逆関数を求めるもので、自由度と確率を指定すれば、対応するt値を計算することができるのです。

まとめ
- t分布
⇒母集団の標準偏差が未知の場合において、標本の標準偏差を用いて標本平均を標準化したときの値「t」が従う確率分布 - 活用の用途
⇒母平均の検定と推定
無相関の検定
回帰分析の偏回帰係数の検定 - 期待値と分散
⇒期待値:$0$、分散:$n/n-2$ - エクセルでの求め方
⇒T.DIST関数で、確率密度関数と累積分布関数を計算できる - t分布のグラフの特徴
⇒左右対称の形状を示す
無限大で正規分布に収束する - t分布表
⇒横軸に確率$p$、縦軸に自由度を取って、マトリックスの交差する箇所に対応するt値が記載された表
一般的な統計調査で母分散があらかじめ分かっているケースは稀です。
そのため、母平均の区間推定を行う上で、t分布の考え方は統計学の必修科目と言えます。
ぜひ使い方を覚えて、実務で活用できるようにしておきましょう。





コメント