「一様分布ってどのような分布なの?」
「期待値と分散の計算の仕方を知りたい」
「離散型と連続型の違いを知りたい」
このような疑問や悩みをお持ちの方に向けた記事です。
一様分布とは、ある区間における発生確率が全て同じとなる確率分布のことで、最も単純で基本的な分布の一つです。
例えば、サイコロの目のように全ての目が1/6の確率で出る事例やルーレットの目の事例など、身近なものも多くみられます。
この記事では、一様分布の定義、期待値と分散の導出の仕方、離散型と連続型の違いや特徴について解説しています。
他の確率分布と比べて計算も簡単なので、ぜひ覚えておきましょう。
一様分布の種類

一様って、そろっているってこと?
一様分布とは、ある区間における発生確率が全て同じとなる確率分布のことです。
確率変数の性質によって、離散一様分布と連続一様分布に分類されます。
離散型とは、確率変数が不連続な値を取る分布のことで、例えばサイコロの目のように、個数などの計数値が変数となります。
確率変数がある値xを取る場合の確率を確率質量関数f(x)と呼び、離散一様分布のf(x)は、以下のように表されます。
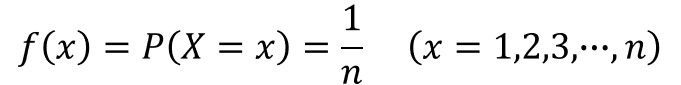
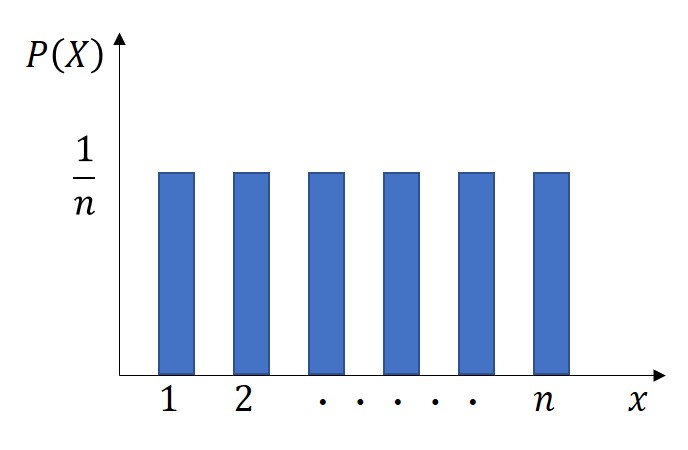
一方、連続型とは、確率変数が連続的な値を取る分布のことで、長さや質量といった計量値が変数となります。
連続型の場合、確率変数がある値xにおける発生のしやすさを関数に表した確率密度関数f(x)が用いられ、連続一様分布のf(x)は、以下のように表されます。
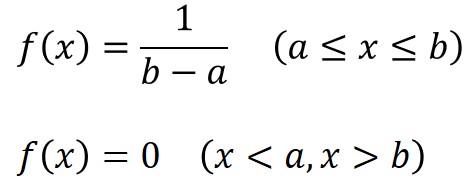
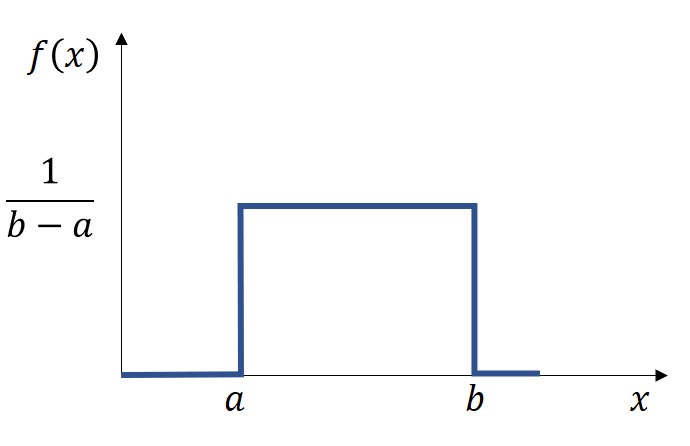
いずれも、総区間の確率の総和が1であることは、共通した性質です。
確率分布の種類、確率密度関数の特徴については、別の記事で詳しく解説していますので、合わせて参考にしていただければと思います。


離散一様分布
期待値と分散
離散一様分布の期待値E(X)と分散V(X)は、以下の数式で求めることができます。
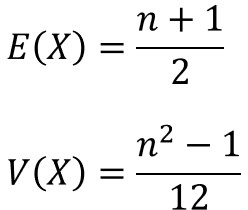
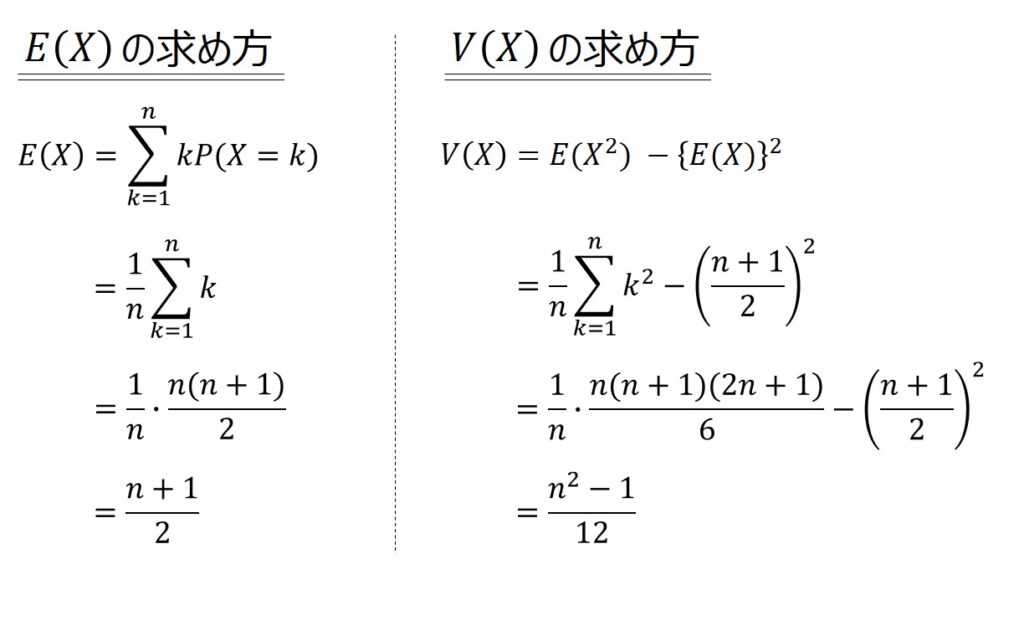
累積分布関数のグラフ
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、以下の数式で定義されます。
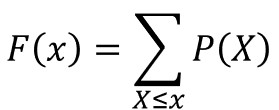
離散一様分布の場合、確率変数が自然数となるので、離散的な点のデータが並ぶグラフになります。
自然数の間の区間は、小数点以下を切り捨てた自然数と同じ値になるので、累積分布関数は階段状になることが特徴的です。
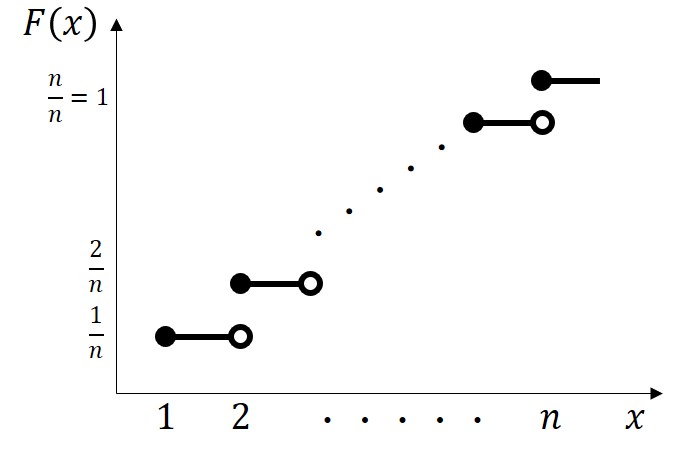

タクシー料金のグラフと似てるね
連続一様分布
期待値と分散
連続一様分布の期待値E(X)と分散V(X)は、以下の数式で求めることができます。
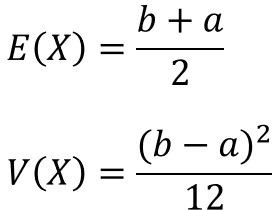

累積分布関数のグラフ
連続型の場合、以下の数式で定義されます。
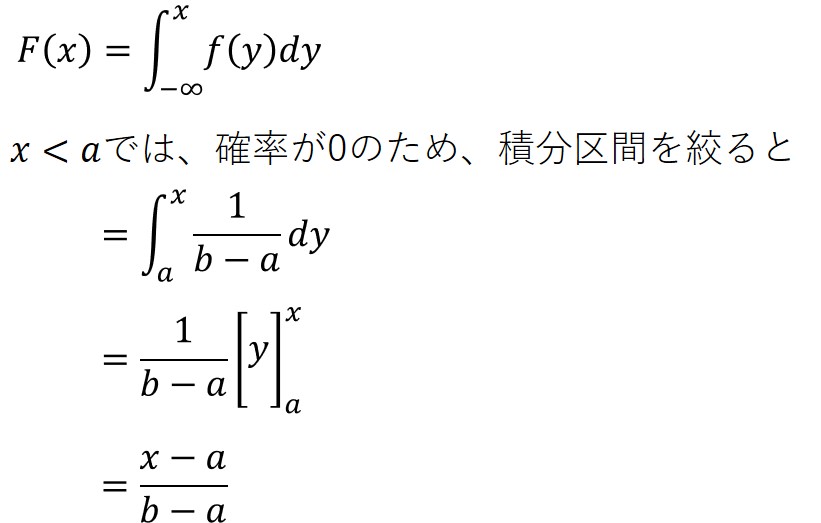
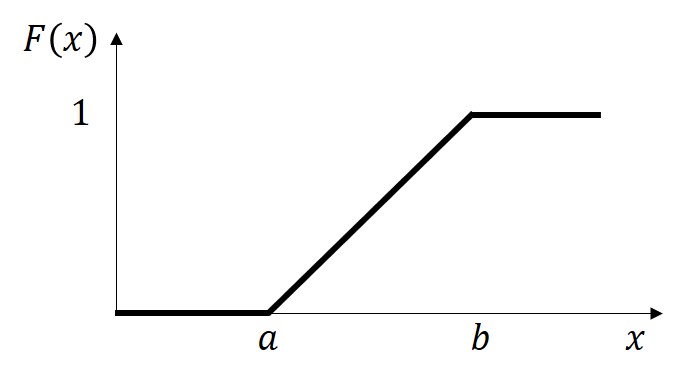
連続一様分布の場合、確率変数が連続的な値を取るので、以下のように一定の傾斜を持ったグラフになります。
確率の総和は1になるので、グラフの縦軸は、0~1の範囲内となります。
例題
まとめ
- 一様分布
⇒ある区間における発生確率が全て同じとなる確率分布のこと - 期待値
⇒離散型:(n+1)/2
⇒連続型:(b+a)/2 - 分散
⇒離散型:(n^2-1)/12
⇒連続型(b-a)^2/12
「一様」という名前だけ見ると、難しそうな印象がありますが、とてもシンプルで分かりやすい確率分布なので、ぜひ覚えておきましょう。
最後まで読んでいただき、ありがとうございました。
この記事で紹介した一様分布は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。







コメント
サイコロの例題について
分散は12で割るのでは?
(20^2-1)/12=33.25
ではないでしょうか?
ご指摘をありがとうございます。
分母の記載に誤記がありましたので、修正いたしました。