QC検定3級の受検をお考えの皆さま、試験対策は順調に進んでいますか?
この記事では、基本統計量に関して、過去問の出題傾向、押さえておきたいポイントを紹介しています。
さらに、模擬問題と解説も合わせて掲載していますので、ぜひ参考になればうれしいです。
また、Youtubeチャンネルでは模擬問題の解説に加えて、基本統計量の基礎知識についても動画で解説していますので、あわせてご覧いただけると幸いです。
過去問の出題傾向
基本統計量は、QC検定3級の試験問題で頻出の分野のひとつです。
2018年から2021年までの6回の試験のうち、計4回で登場しています。
計算の内容はそれほど複雑ではありませんが、用語の定義や変数変換のやり方など、基本を把握しておかないと最初の段階で詰ってしまうので、しっかり覚えておきましょう。
問題の内容としては、大きく以下に分かれます。
- 平均値、不偏分散、標準偏差を計算する問題
- 最大値、最小値、中央値、範囲を選ぶ問題
- 変数変換を扱う問題
押さえておきたいポイント3選
その1:不偏分散は公式を覚えるべし
分散とは、平均値に対する各データの差分(偏差)の二乗和をサンプルの大きさで割ったもので、不偏分散の定義の式は以下で表されます。
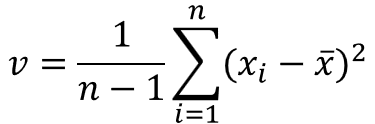
これを真面目に解こうとすると、データ一つずつに対して平均値との差分をとって、それを二乗する必要があるので、結構な計算の労力を費やします。
そこで、QC検定を受検の方には必須と言える偏差平方和の公式ですが、以下を覚えておきましょう。
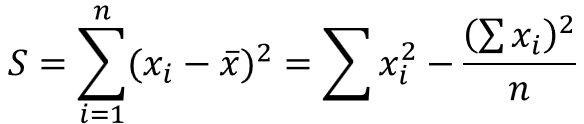
そして偏差平方和から不偏分散は以下のように求められます。
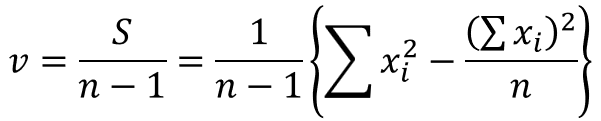
「二乗の和」と「和の二乗」、「サンプルサイズ」が分かれば計算できるので、電卓を叩く回数を大幅に減らすことができます。
公式の導出の過程は以下の通りです。少し難しいですが、丸暗記ではなく一度は目を通しておくと良いでしょう。
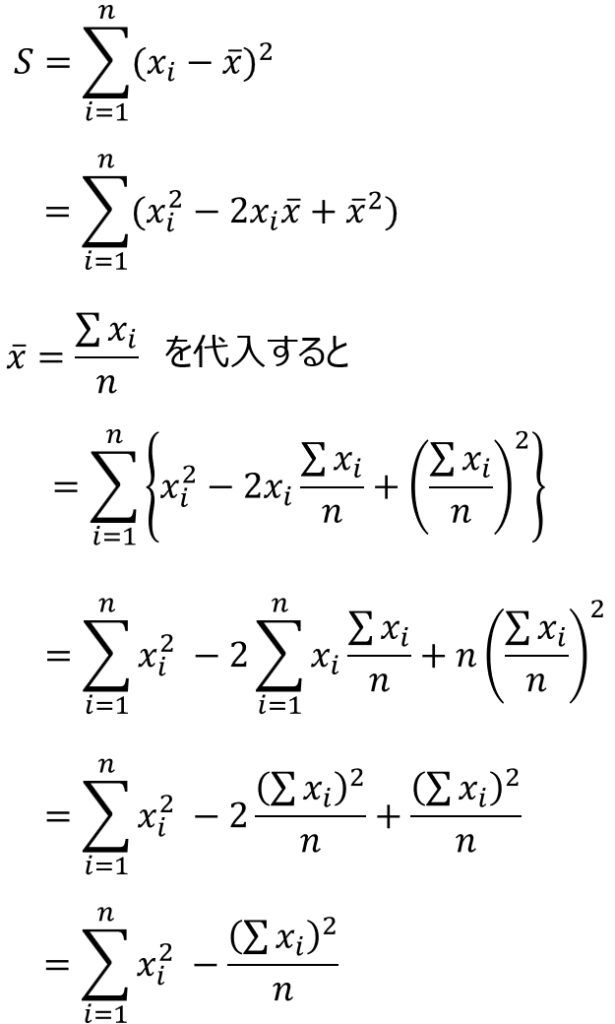
その2:分散と標準偏差の取り違いに注意
うっかりミスでありがちなのが、分散と標準偏差を間違えて選んでしまうケースです。
分散の平方根を取れば標準偏差が求められるので、計算の過程もほぼ同じです。
さらに厄介なことに、標準偏差と分散の両方の値が選択肢の中に入っていることがあります。
私自身も過去問を解いていて何度かミスした経験がありますが、分散を計算して出てきた結果が選択肢にあったので選んだら、実は標準偏差を求める問題だったなんてことも。
最後の最後で勘違いしてケアレスミスしても得点にはなりませんので、一通り解き終わって見直す際にも、十分注意を払っておきましょう。
その3:変数変換は戻すときに注意
変数変換は、元データの数値が大きい場合や小数点以下の数値を扱う場合に計算を簡略化できるのでとても便利です。
計算のやり方も単純で、例えば以下のように基準値を設けて全体をオフセットし、小数点以下の桁を上げることで、変数変換ができます。
以下の例では基準値を170、小数点以下を10倍しています。
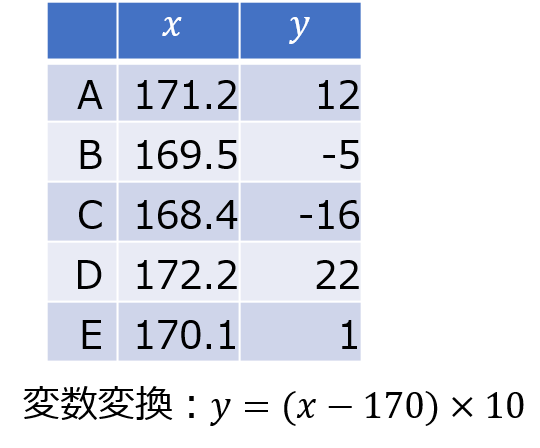
ここで注意が必要なのが、変数変換して平均値や分散を求めたあと、最後に元の変数に戻すときの計算のしかたです。
平均値はそのまま逆の手順として、桁を下げて、基準値のオフセット分を戻せばよいです。
では、分散はどのように戻せばよいかというと、単位系が平均値の二乗になるので、同じように桁を二乗して計算する必要があります。
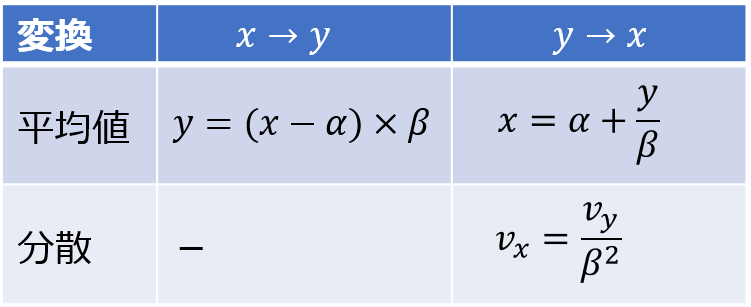
平均値は直感的にも理解しやすいので、10倍か100倍か、あるいは1/10か1/100か、直感的に判断できると思います。
ただ、分散になった途端にイメージとして掴みにくくなるので、どうやって戻せばよいか混乱してしまうことがあります。
特に10倍か100倍か、選択肢にも紛らわしいものが入っている場合があるので、気を付けておきましょう。
模擬問題
基本統計量に関する練習問題を2つ用意しました。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題1

問題2

解説1

解説2
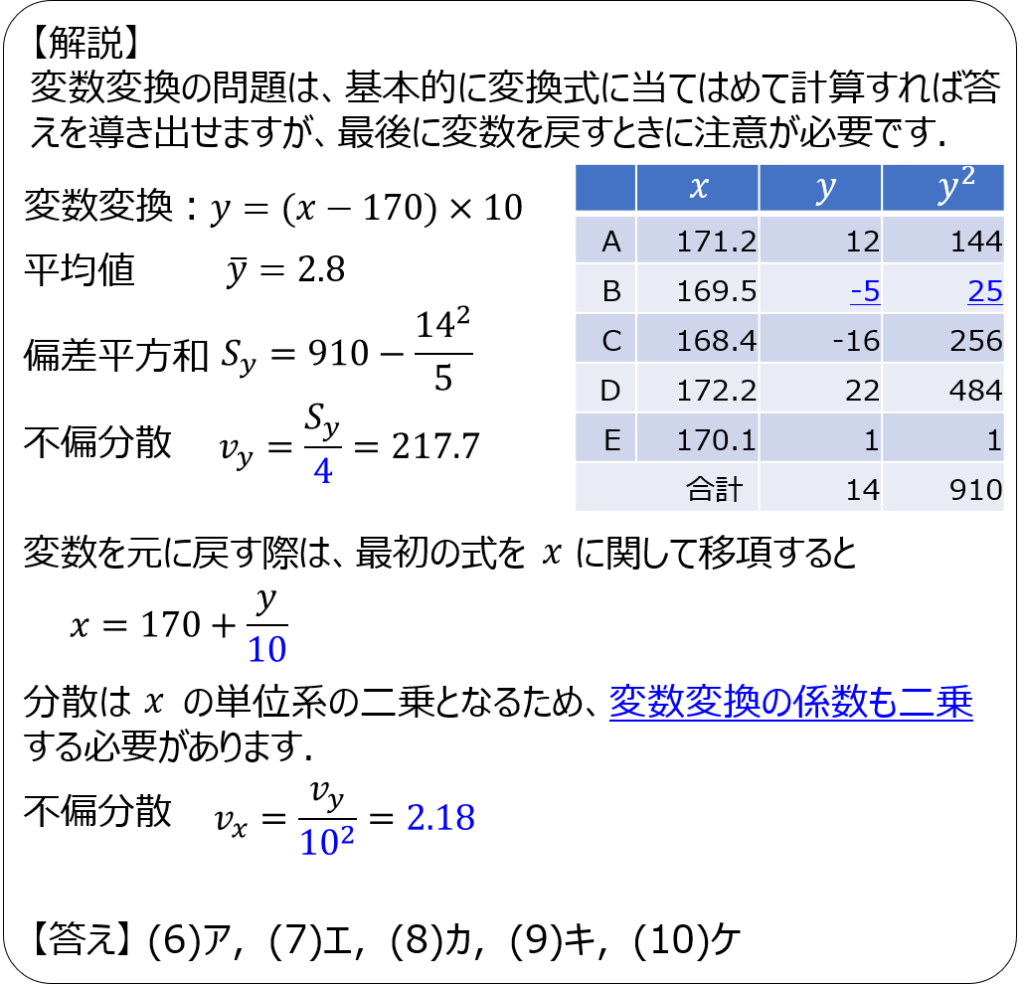
その他の模擬問題の一覧はこちらをどうぞ。

なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。

それでは、皆さまのご健闘をお祈りしております。





コメント