QC検定2級の受検をお考えの皆さま、試験対策は順調に進んでいますか？
この記事では、2級の中でも頻出の統計的区間推定について、過去問の出題傾向と押さえておきたいポイントを紹介しています。
さらに、模擬問題と解説を合わせて掲載していますので、ぜひ参考になればうれしいです。
また、Youtubeチャンネルでは模擬問題の解説に加えて、区間推定の基礎知識についても動画で解説していますので、あわせてご覧いただけると幸いです。
過去問の出題傾向
最初に頻出と言っておきながら、実は区間推定（信頼区間の幅の推定）は単独の大問で出題されることはあまりありません。
私の勝手な推測ですが、区間推定では計算式や計算結果を問われることが多いですが、大問として取り上げるほどの設問数がないことによるのではと思います。
そのため、区間推定は統計的検定の大問の一部として登場することが多いです。
実際に、2018年から2021年までの6回の試験のうち、区間推定は2回で出題されていますが、いずれも検定の小問の一部となっています。
ただ、統計的検定は6回のうち5回に登場する最頻出分野の一つで、考え方も区間推定と似ているので、混乱しないようにどちらも得点源とできるようにしておきましょう。
先ほども述べた通り、問題の内容はとてもシンプルです。
- 信頼区間の計算式を選ぶ問題
- 信頼区間を計算する問題
押さえておきたいポイント3選
その１：Kpとｔ値の確率の取り方に注意
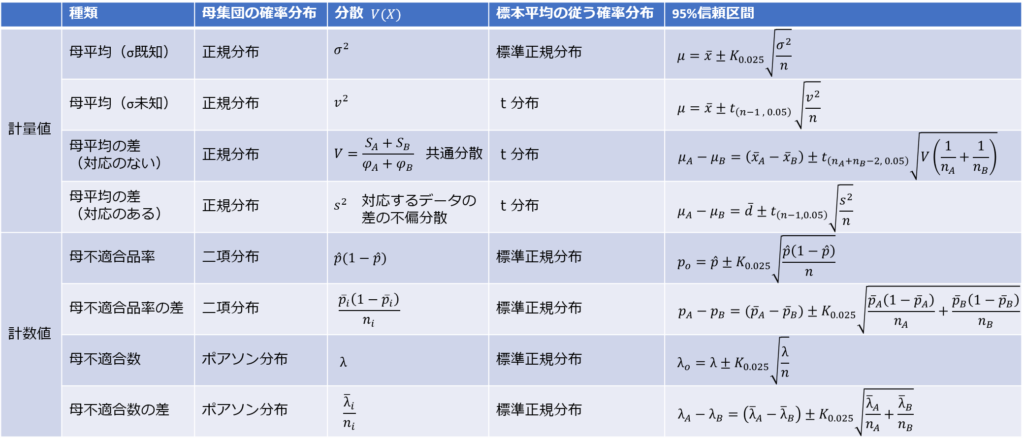
最初に、信頼区間の計算式の一覧を紹介します。
※95%信頼区間
こんなにたくさんの種類があるのか・・・と気持ちが萎えてしまいそうですが、残念ながらQC2級の出題分野としては全てを理解しておく必要があります。
そして、統計的推定や統計的検定で最も多いつまづきポイントの一つと言えるのが、Kp値とｔ値の確率の取り方です。
一覧表を見ていただいてわかる通り、Kpやｔの右下に小文字で0.05や0.025といった数値が記載されています。
これは有意水準に該当する確率を表していますが、95%信頼区間を求める場合でも、0.05や0.025といった二つの数値が登場して、どちらを使えば良いのか混乱しがちです。
さらに混乱を助長させるのが、統計的検定には片側検定と両側検定があり、同じ有意水準でも用いるKp値やｔ値が両者で異なります。
そこで、あらためて理解しておきたいのが以下の概念図です。
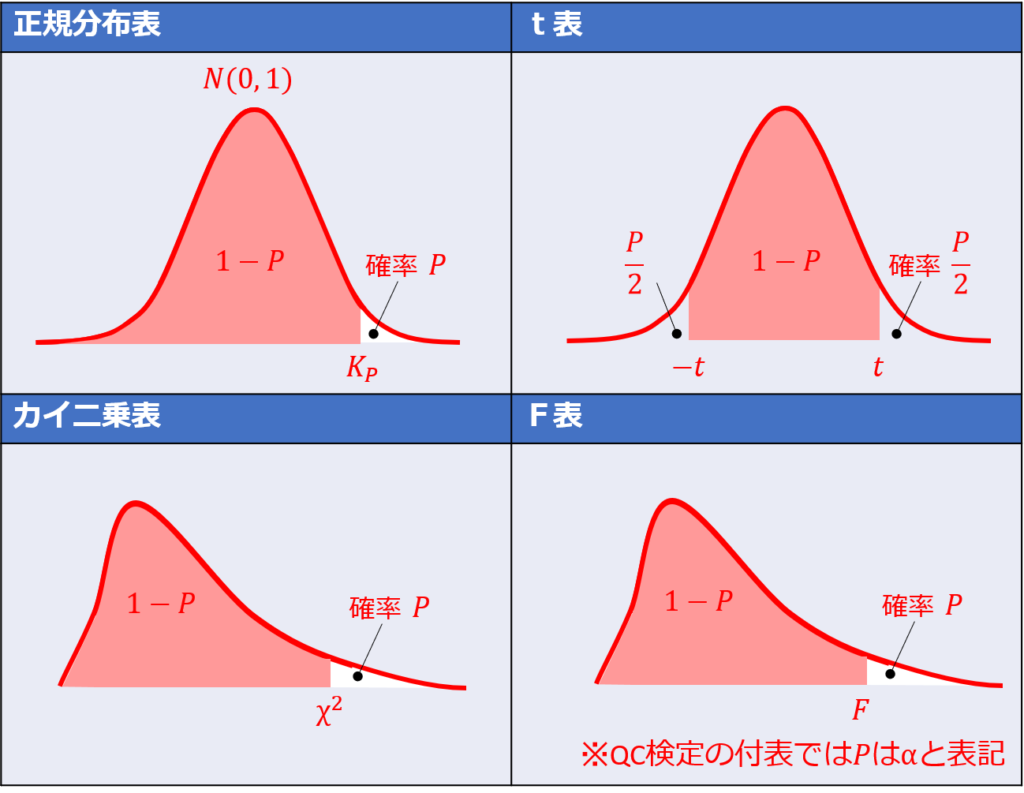
QC検定で与えられる付表では、標準正規分布は上側確率、ｔ分布は両側確率、カイ二乗分布とＦ分布も上側確率となっています。
そのため、95%信頼区間を求める場合、以下の例のように付表から読み取る確率Ｐの値が異なることを認識しておきましょう。
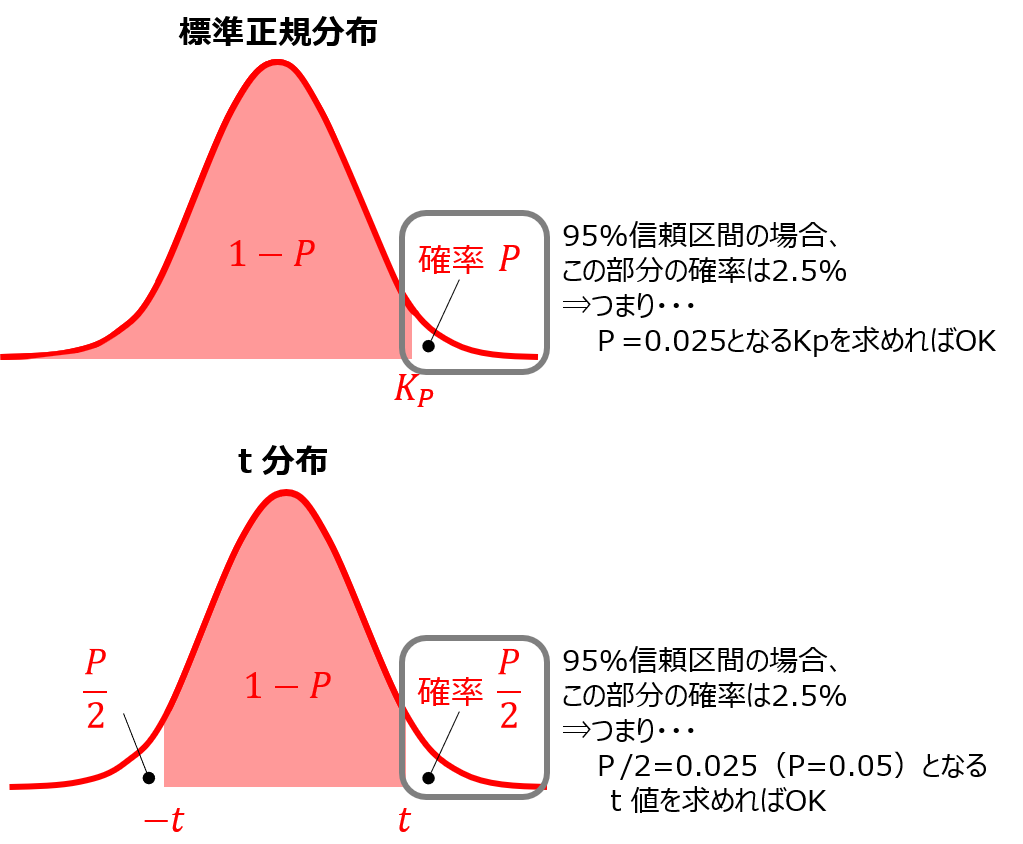
その２：分散の区間推定は要注意
先ほどの一覧表から分散に関するものを抜粋してあらためて記載します。
他の種類と比べて、数式の形が異なることがひと目でわかると思います。
この式のややこしいのが、分母と分子がどちらなのか、上側確率と下側確率がどちらなのか直感で理解しがたく、丸暗記だけではとても正確に覚えきれないことです。
さらには0.975といった確率まで登場して、似たような選択肢に圧倒されて、さっぱり分からない状態に陥ってしまうのです。
ここで覚えておいていただきたいのは、カイ二乗分布とＦ分布は左右非対称の確率分布であることです。
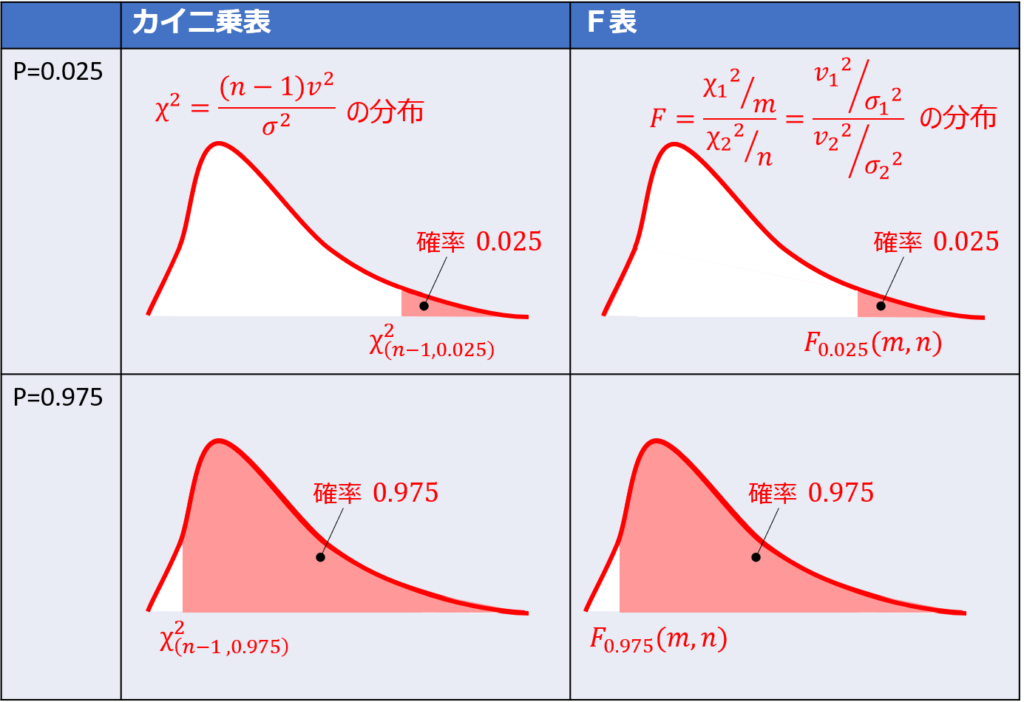
左右非対称ということは、2.5%点と97.5%点をそれぞれ求める必要があるということで、0.975が計算式に登場するのは、この理由によるものです。
また、分母と分子の関係性については、カイ二乗値とＦ値の定義を覚えておくようにしましょう。
この定義の式を覚えておけば、自分で式を変形して信頼区間の式を導出することができるので、似たような選択肢に惑わされることもなくなります。
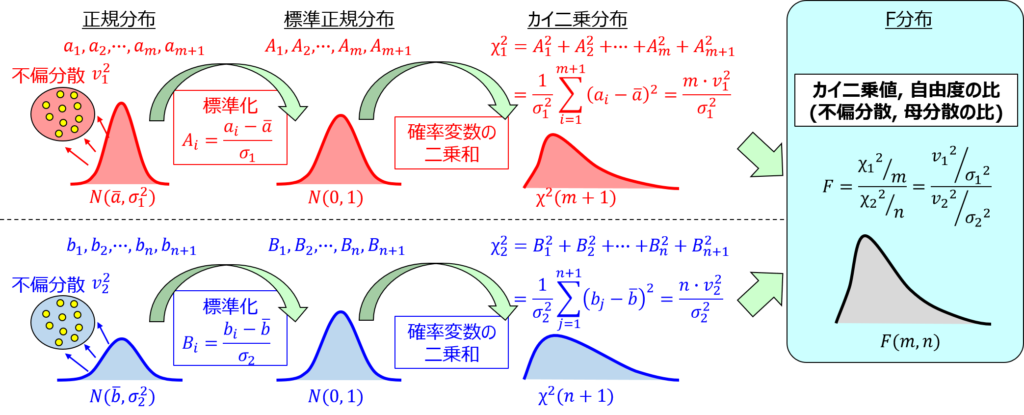
式の変形といっても簡単な分数の変形なので丸暗記よりも応用が利きやすく、確率分布の本質の考え方を理解する方がよほど為になるのでおススメです。
その３：式の基本形はほぼ同じ
分散に関する計算式は先ほど説明した通りですが、それ以外は式の基本形がほぼ同じです。
これは、正規分布$N(μ, σ^{2})$の母集団から抜き取った標本平均は$N(μ, σ^{2}/n)$に従う考え方にもとづいています。
分散$σ^{2}/n$は、すなわち標準偏差$\sqrt{σ^{2}/n}$を意味し、まさに$K_{p}\sqrt{V/n}$は標準偏差が何個分の幅に該当するか、ということを表しています。
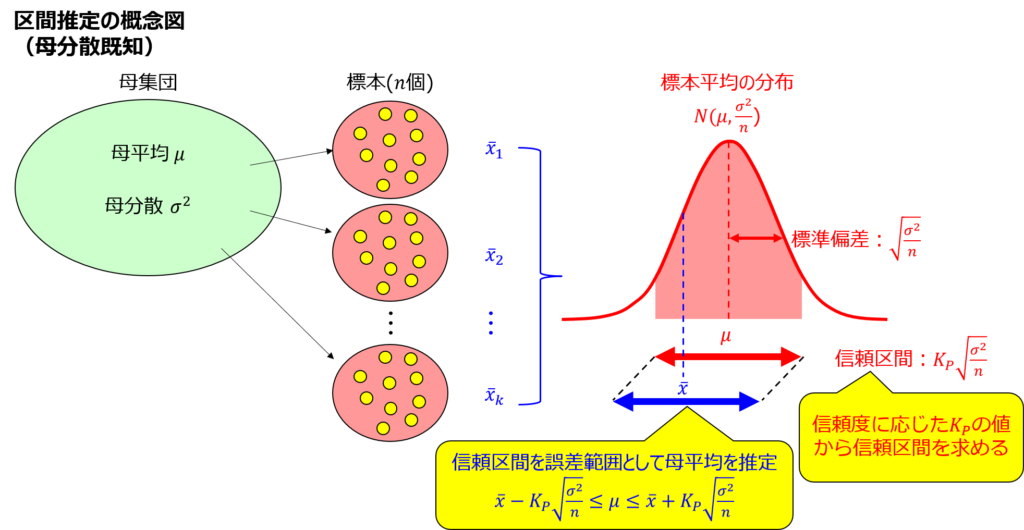
これは母平均の区間推定に限らず母平均の差や母不適合品率にも当てはまるので、式の意味を理解しておけば、あとは分散の計算式を覚えるだけで信頼区間の幅を導出できるわけです。
模擬問題
区間推定に関する練習問題を5つ用意しました。
それぞれ答えと解説も記載していますので、合わせてご覧ください。
問題１
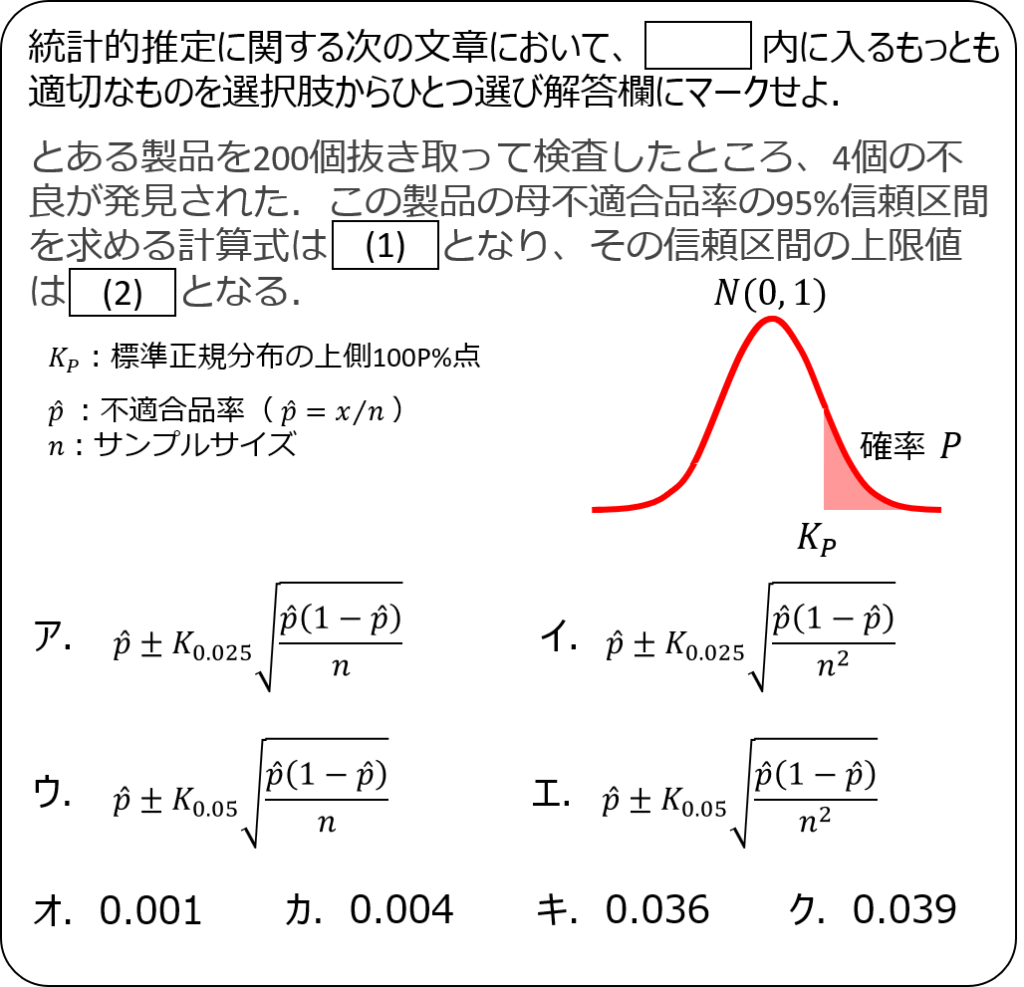
問題２
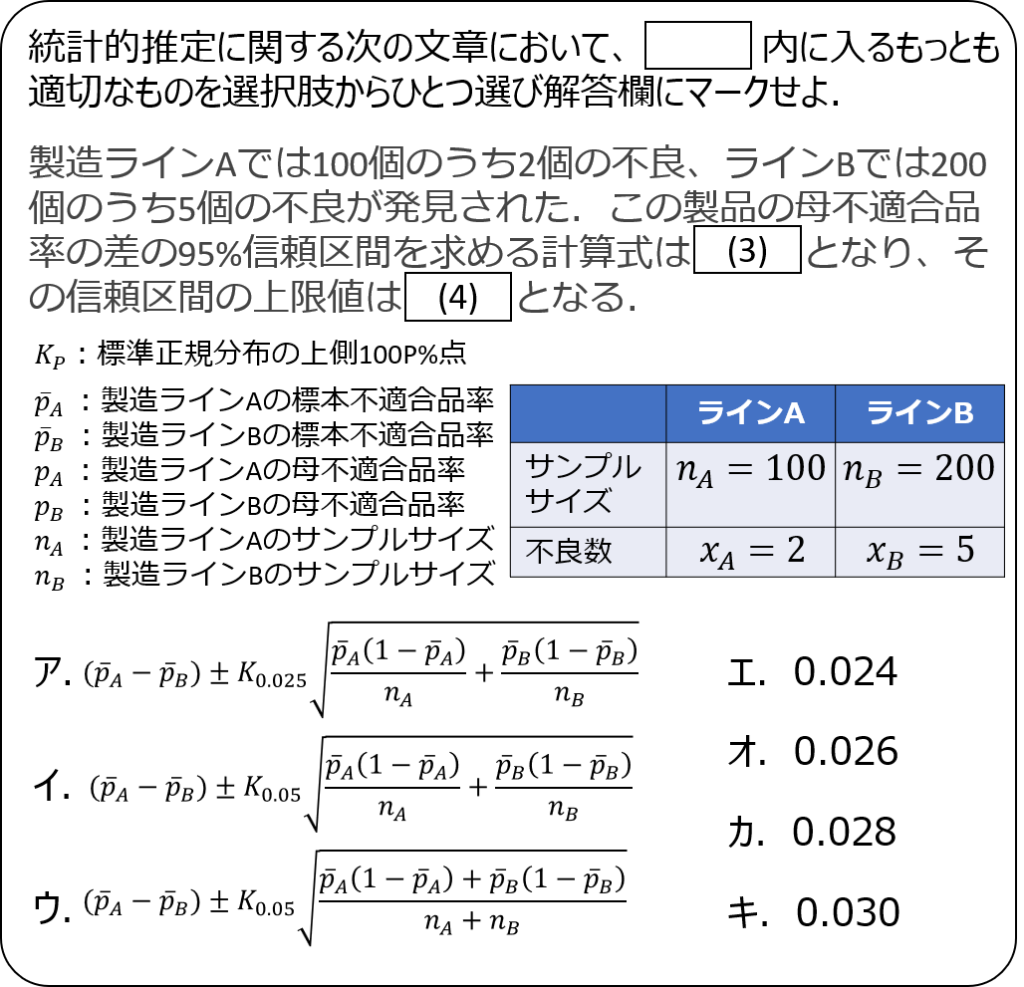
問題３
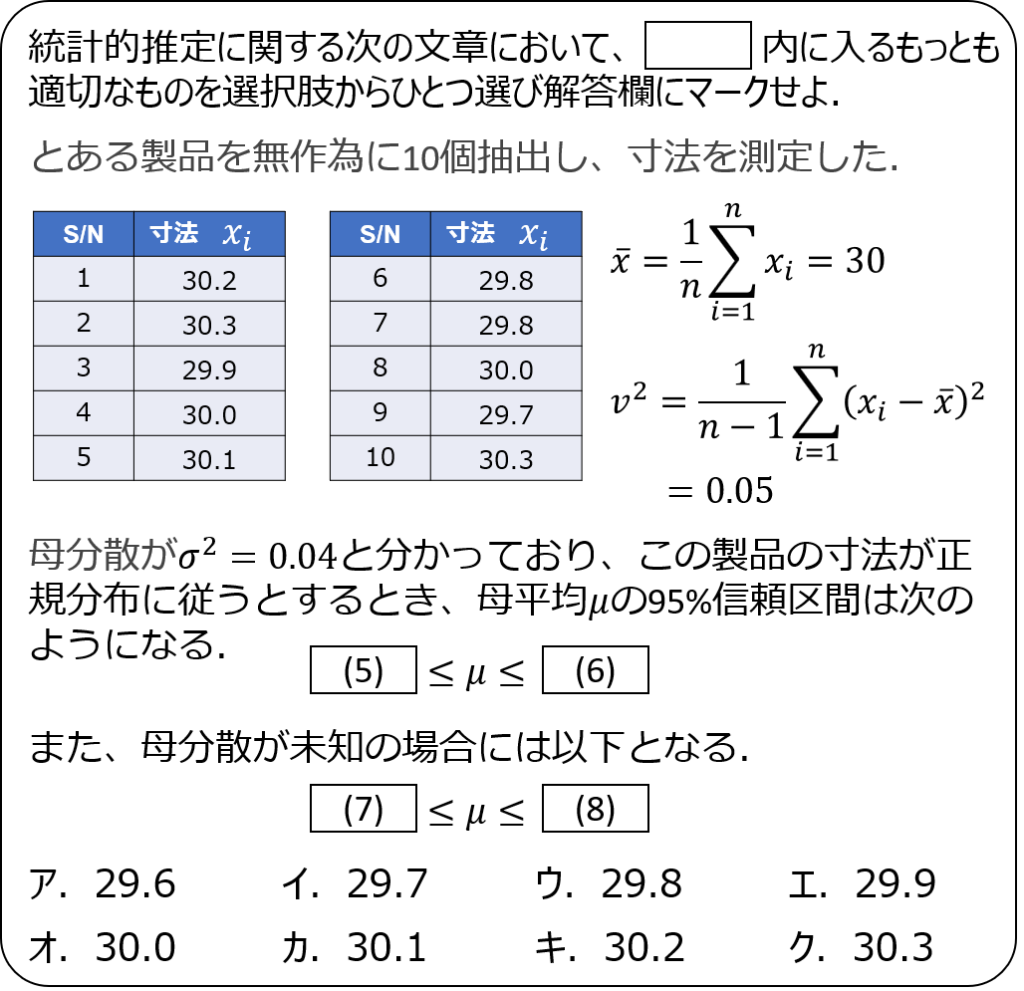
問題４
問題５
解説１
解説２
解説３
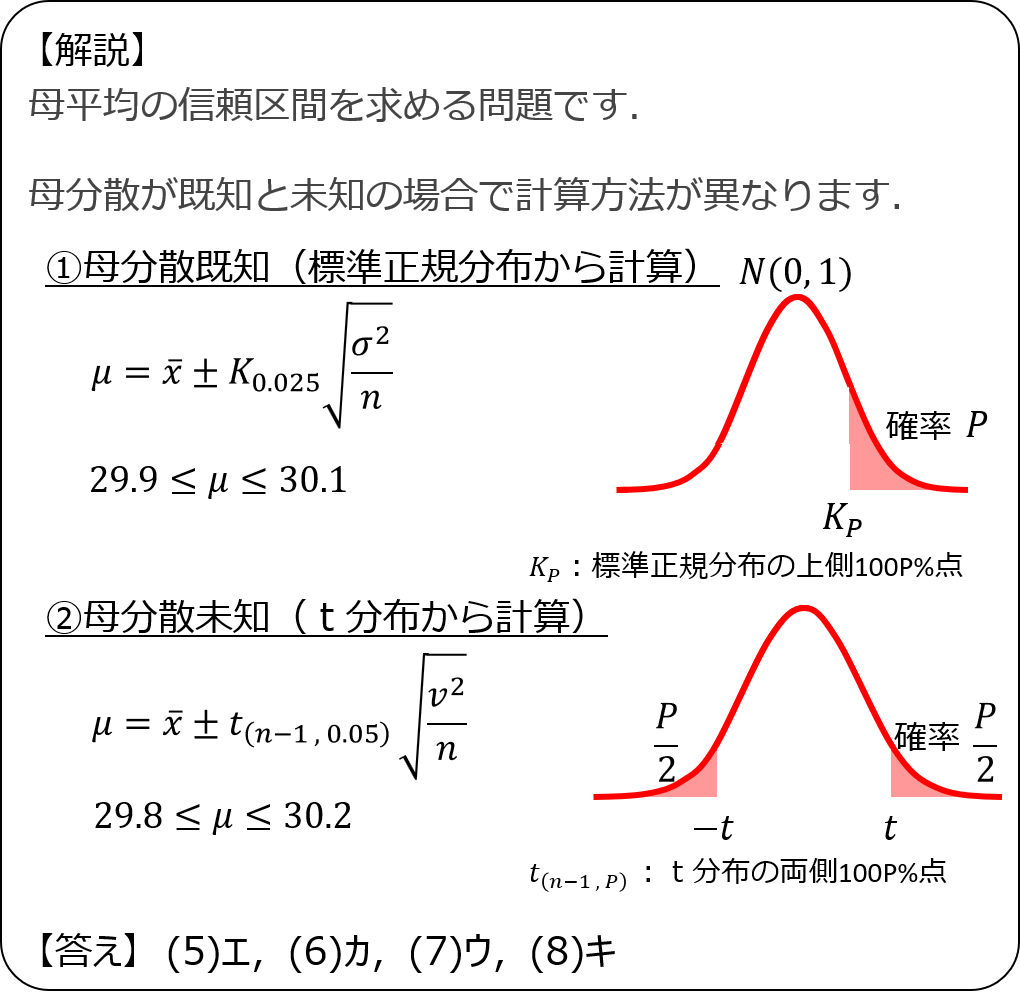
解説４
解説５
統計的推定や統計的検定の基本から学び直したいかたに向けては、以下の記事で詳しく解説しています。
シリーズ編になっているので、苦手分野のあるかたはスポットで、全般的に学習したい方は「その１」からご覧ください。
なお、QC検定のおすすめ勉強方法や教材については、以下の記事で詳しく紹介していますので、合わせてご覧ください。
それでは、皆さまのご健闘をお祈りしております。
コメント