この記事では、母分散の信頼区間の計算方法、計算式の構成について、初心者の方にもわかりやすいよう例題を交えながら解説しています。
母分散の信頼区間は、この記事で完結して解説していますが、標本調査の考え方など、区間推定(その1)の記事から段階を追って説明しています。
さまざまな区間推定の種類を網羅的に学習したい方は、ぜひ最初から読んでみてください。

カイ二乗分布とは?
定義
母分散の信頼区間を求めるには、カイ二乗分布を使います。
まず、早速登場した「カイ二乗分布」という用語、名前を聞くだけで敬遠したくなりますよね・・。
区間推定を求めるのに細かい数式を覚える必要はないので、ここではカイ二乗分布の概念だけ覚えておいてください。
「カイ」は記号で「$χ$」と表され、以下の数式によって定義されます。
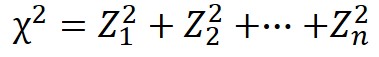
ここで、$Z_{1}~Z_{n}$は標準正規分布に従う互いに独立な確率変数を表します。
標準正規分布とは、正規分布において平均値$μ$を$0$、標準偏差$σ$を$1$として基準化したもので、$N(μ,σ^{2})$は$N(0,1)$と表記されます。
この$χ^{2}$が従う確率分布のことをカイ二乗分布と呼び、自由度$n-1$のカイ二乗分布に従うと表現されるのです。
確率変数の二乗和が従う分布なので、すなわち、「ばらつき」「分散」に関わる確率を求める場合に活用されます。
母分散の信頼区間を求めるほかに、独立性の検定や適合度の検定など、同じく分散を扱う検定にも用いられます。

いろいろな使い道は覚えておこう
カイ二乗分布のグラフの特徴
カイ二乗分布のグラフは左右対称ではなく、右側に裾広がりの形状を示します。
以下のグラフは、自由度の違いによる確率密度関数の形状の違いを表したものです。
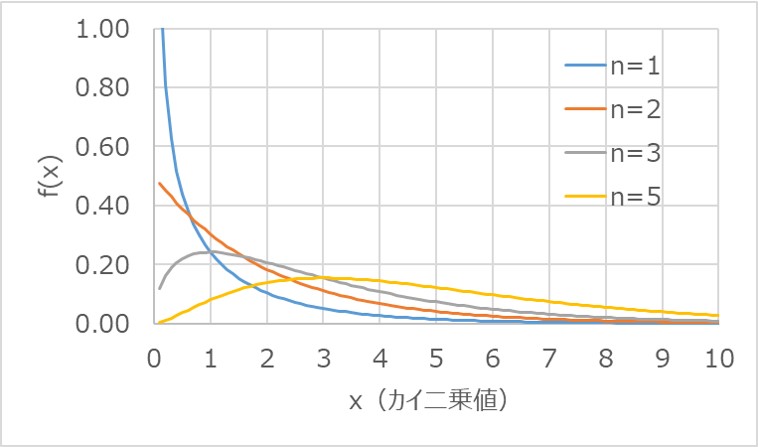
いずれも、右側に広がった分布を示していることが分かります。
二乗和を扱う統計量の分布なので、特に自由度が小さい場合に偏った形状が顕著に表れます。
ここまで説明したカイ二乗分布について、以下の記事で期待値や分散、エクセルでのグラフの書き方を詳しく解説していますので、合わせてご覧ください。

母分散の信頼区間の求め方
信頼区間の計算式
カイ二乗分布では、分布の横軸(カイ二乗値)に対して、全体の何%を占めているのか対応する確率が決まっており、エクセルのCHISQ.DIST関数やカイ二乗分布表で簡単に求められます。
そして、このカイ二乗値を係数として用いることで、信頼度○○%の信頼区間の幅を計算することができるのです。
母分散の95%信頼区間の計算式は、以下のように表されます。
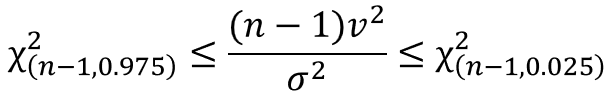
$σ^{2}$は母分散、$v^{2}$は不偏分散、$n$はサンプルサイズを表します。
$χ^{2}$はカイ二乗値を意味し、例えばサンプルサイズが$n=10$で信頼度95%とすると、$χ^{2}(n-1, 0.025)=19.02$となります。
カイ二乗分布の確率密度関数のイメージで書くと次のようになります。
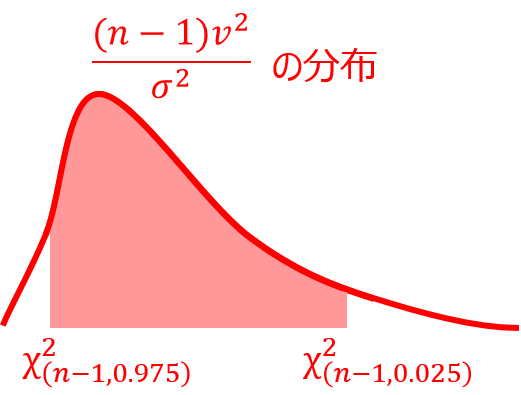
ちなみに、平方和(平均値との差の二乗和)を自由度$n-1$で割ると不偏分散になるので、先ほどの式は次のように表現することもできます。
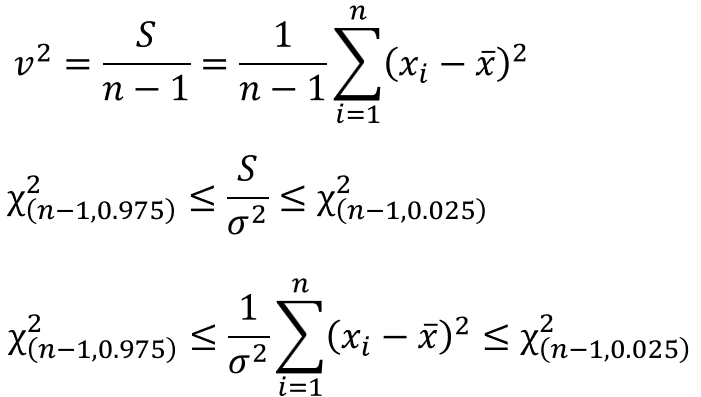
カイ二乗分布の定義の式(二乗和)に近い形となり、この統計量がカイ二乗分布に従うことのイメージが掴みやすくなったのではないかと思います。
計算の手順
それでは、実際に母分散の区間推定をやってみましょう。
以下は、とある製品を無作為に10個抽出し、寸法を測定した結果です。
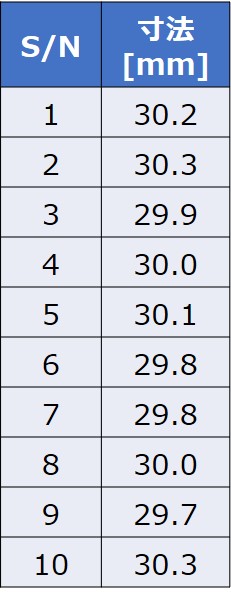
この製品の寸法の分布が正規分布に従うとするとき、母分散の95%信頼区間はいくらとなるでしょうか?
1.不偏分散を求める
まずは標本のデータから不偏分散を計算します。
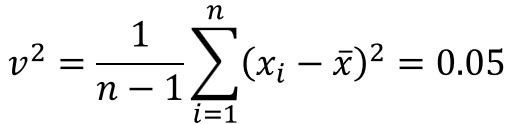
不偏分散と標本分散をうろ覚えの場合はこちらも参考にどうぞ。

2.カイ二乗値を求める
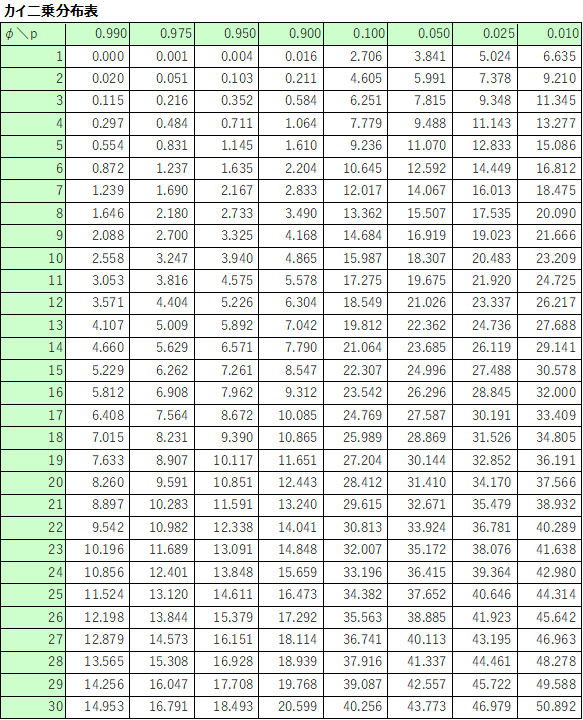
次に信頼度に相当するカイ二乗値をカイ二乗分布表から求めます。
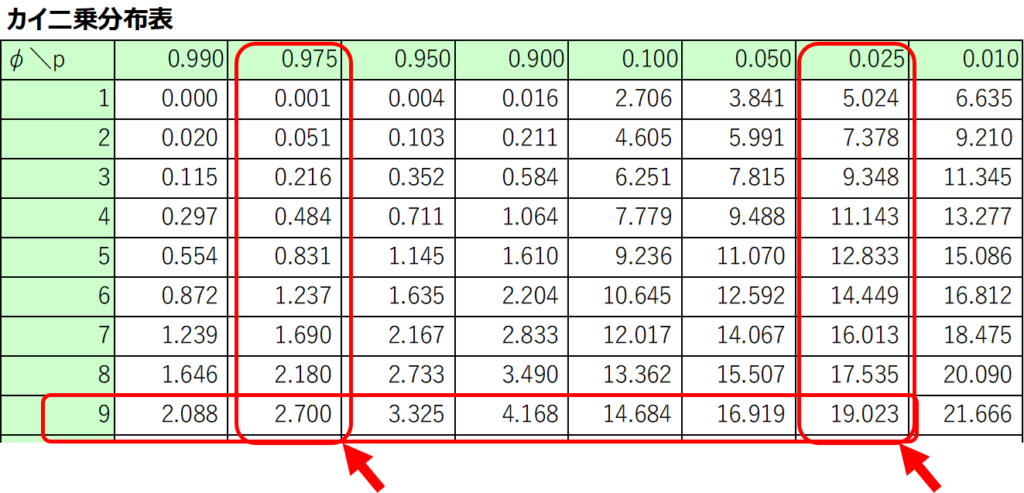
カイ二乗分布表とは、横軸に確率$p$、縦軸に自由度$φ$を取って、マトリックスの交差する箇所に対応するカイ二乗値が記載されている表です。
ここで表す確率$p$は、カイ二乗値に対する上側確率を意味します。
つまり、カイ二乗値がとある値よりも大きくなる確率を表しています。
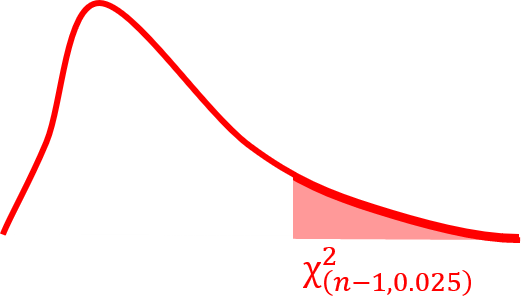
一つ注意点として、カイ二乗分布は横軸に対して左右対称ではないので、信頼度に対して上側と下側のそれぞれに相当するカイ二乗値を求める必要があります。
例えば、信頼度95%(0.95)の上側確率にあたる自由度9のカイ二乗値は、$χ^{2}(9, 0.025)=19.02$、下側確率のカイ二乗値は、$χ^{2}(9, 0.975)=2.70$と読み取ることができます。
ちなみに、エクセルではCHISQ.INV.RT関数を用いることで、対応するカイ二乗値を求められます。
CHISQ.INV.RT関数とは、カイ二乗分布の上側(右側)確率の逆関数を表し、今回の事例の場合、$=CHISQ.INV.RT(0.05/2, 9)=19.02$として同じ結果が得られます。

関数なしでふつうに計算したら大変だよ・・
3.信頼区間を計算する
区間推定の定義の式に信頼区間95%のカイ二乗値を入れると、以下の不等式が成立します。
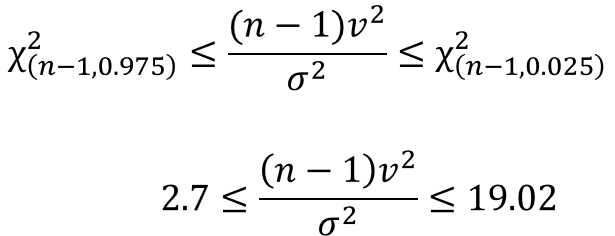
そして、これを$σ^{2}$に対して変換すると、次のようになります。
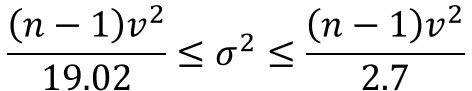
あとは、不偏分散、サンプルサイズを代入すると、母分散の信頼区間を求めることができます。
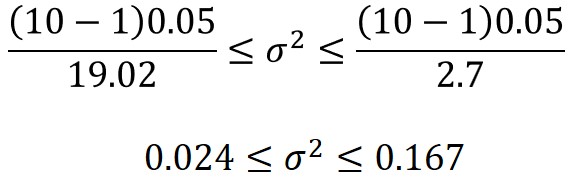
つまり、この製品の寸法の母分散は、信頼度95%の確率で0.024~0.167に収まるという推定結果になります。
まとめ
- 母分散の信頼区間の求め方
⇒カイ二乗分布を用いる - 計算の手順
⇒①:不偏分散を求める
②:信頼度に対応するカイ二乗値を求める
③:母分散の推定値を計算する
最後まで読んでいただき、ありがとうございました。




コメント