「中心極限定理ってどういう定理なの?」
「どのようなメリットがあるの?」
「数式だけではイメージが掴みにくい」
このような疑問や悩みをお持ちの方に向けた記事です。
中心極限定理とは、平均値$μ$、分散$σ^{2}$の確率分布から$n$個を抽出する際、標本平均$\bar{x}$は$n$が十分大きい場合において、$N(μ, σ^{2}/n)$に従うという定理です。
二項分布や指数分布など、どのような確率分布においても当てはまる定理で、複雑な確率の計算を正規分布に置き換えて簡単に求めることができるので大変便利です。
この記事では、中心極限定理の定義と活用するメリット、グラフで視覚的に理解するためのエクセルを用いたシミュレーションを紹介しています。
初心者の方にもわかりやすいよう、できるだけ細かく手順を踏んで説明しますので、参考になればうれしいです。
中心極限定理とは?
全数調査と標本調査
中心極限定理とは、平均値$μ$、分散$σ^{2}$の確率分布から$n$個を抽出する際、標本平均$\bar{x}$は$n$が十分大きい場合において、$N(μ, σ^{2}/n)$に従うという定理です。
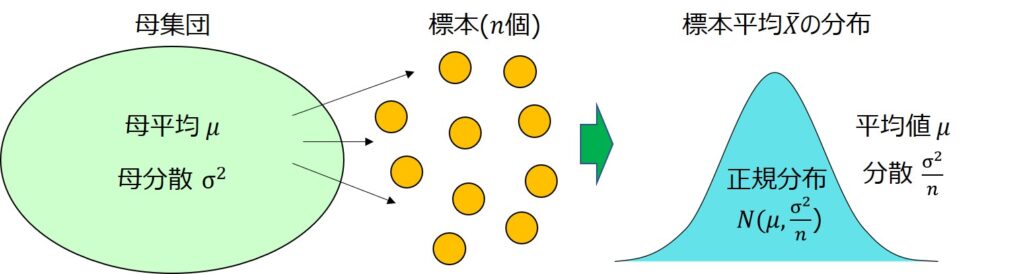
「十分に大きい」というのは一般的には$n$が50以上の場合を表すことが多いです。
調査には、母集団の全てを調べる全数調査と、全体から代表の一部を選ぶ標本調査があります。
全数調査は正確な統計値が得られるメリットがある一方で、コストや期間がかかることがデメリットです。
選挙の出口調査や視聴率調査など、現実的に全数調査をできないことも多く、日常生活でも標本調査を活用する事例が多くあります。

何でもかんでも全部調べられないもんね
ただし、標本調査を行う場合、平均値や分散といった統計量が母集団と一致することはごく稀で、必ずと言っていいほど、標本の統計量と真の数値(母平均、母分散)には乖離が生じます。
例えば、たまたまサンプリングした標本が、母集団の分布から外れた例外的なものであった場合、標本の統計量を鵜呑みにすることは信頼度が低く、実際の運用上で大変危険です。
そのため、真の数値に対する「乖離の程度」をきちんと把握した上で、コストや手間の省ける標本調査を上手く活用することが重要なのです。

大数の法則との違い
中心極限定理と似た意味の法則として、大数の法則があります。
大数の法則とは簡単に言うと、サンプリング数$n$が十分に大きい場合には、標本平均$\bar{x}$は母平均$μ$に近づくというものです。
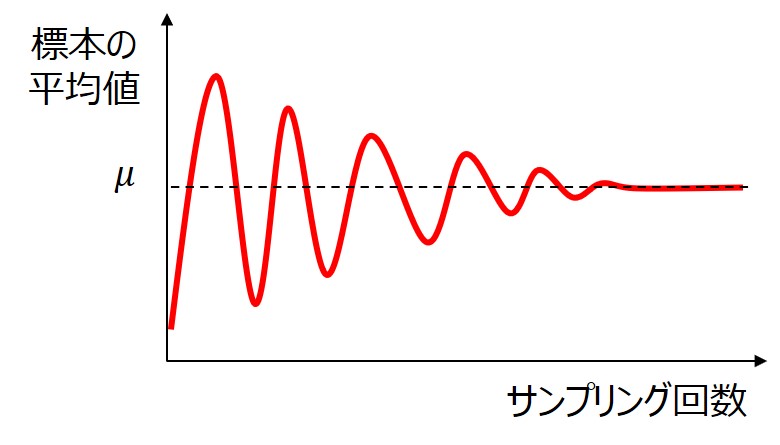
数式での証明は複雑ですが覚える必要はなく、法則の内容自体は感覚的にも理解しやすいと思います。
サンプリング数が少ない場合には、たまたま分布から外れたものを選ぶ可能性がありますが、試行回数を増やすほど偶然の重なる確率が下がり、真の値に収束するという意味です。
ここで、もう一度、中心極限定理の定義を振り返ってみましょう。
平均値$μ$、分散$σ^{2}$の確率分布から$n$個を抽出する際、標本平均$\bar{x}$は$n$が十分大きい場合において、$N(μ, σ^{2}/n)$に従うという定理です。
標本平均が母平均に近づくという意味では、大数の法則と同じことが分かっていただけると思います。
さらに、中心極限定理では、標本平均が従う分布形状(正規分布)、ばらつきの程度(分散$σ^{2}/n$)まで定義されており、すなわち大数の法則をより詳細に表した定理と解釈できます。
中心極限定理を用いるメリット
複雑な計算を簡略化できる
それでは、中心極限定理が使えると何がうれしいのか、具体例を交えてメリットを紹介します。
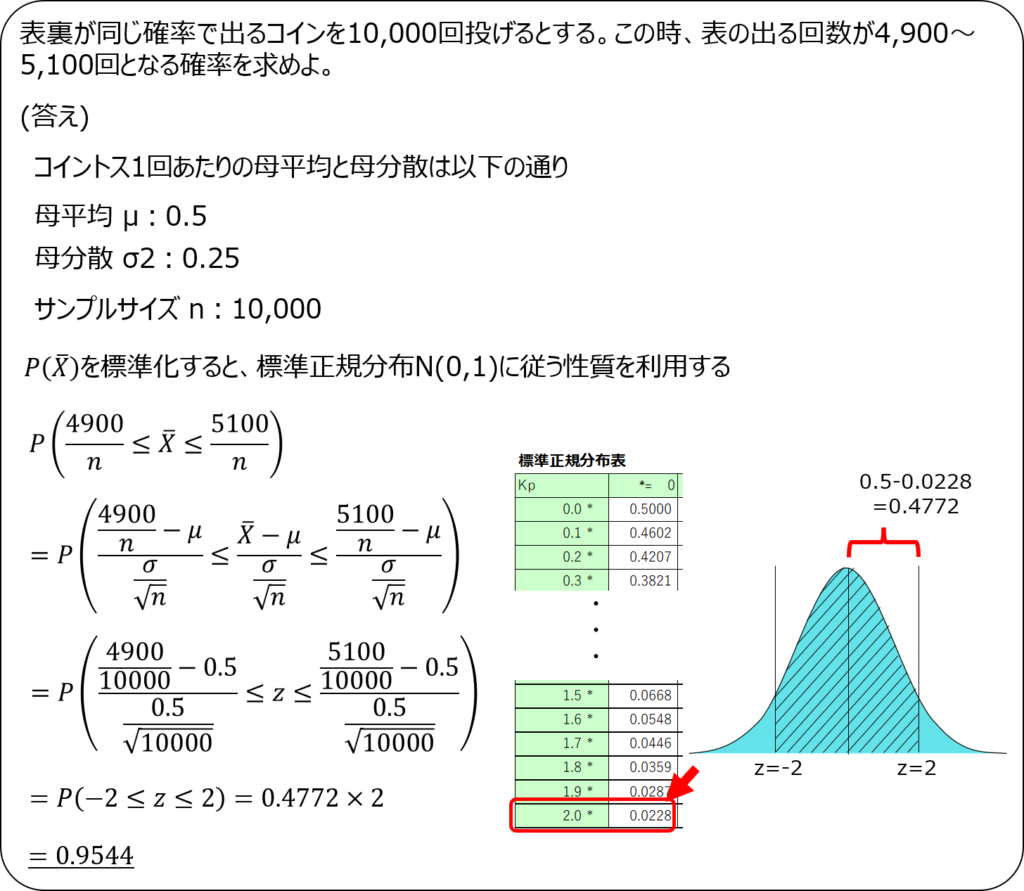
例えば、表裏が同じ確率で出るコインを10000回投げて、表の出る回数が4900回~5100回になる確率を求めたいとします。
この場合、表と裏のいずれかで結果が表されるため、確率は二項分布に従います。
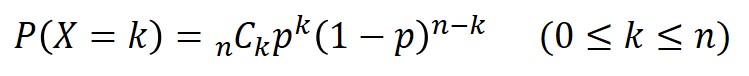

ここで、実際にnとpを当てはめて数式を解こうとすると、壁にぶち当たることに気づきます。
10000C4900のコンビネーション関数は、電卓では到底計算できませんし、残念ながらエクセルを用いても求めることができません。
少なくともExcel 2019までのバージョンでは、計算できる桁数は最大でも308桁までしかありません。
数式は至って単純なのですが、nが十分大きい場合には、そもそも計算ができないのです。
このような場合に、標本平均の分布を正規分布として扱えるのは、確率の計算を非常に簡単にできるので便利です。

エクセルでも計算できる限界があるんだ
簡略化の実例
先ほどの例について、実際に中心極限定理を用いて解いてみましょう。
このように、正規分布に置き換えることで、エクセルの関数(NORM.DIST関数)や標準正規分布表を用いて簡単に確率を求められるのです。

エクセルによるシミュレーション
中心極限定理の意味とメリットはイメージが掴めたとして、本当にどのような分布でも平均値$μ$、分散$σ^{2}/n$の正規分布に従うのか、感覚的に理解しにくいと思います。
ここでは、離散型確率分布の代表例の一つとして一様分布、連続型として指数分布を例に挙げて、$n$数の違いによる標本平均の分布の変化をグラフ化して紹介します。
一様分布と指数分布については、それぞれ別の記事で詳しく解説していますので、合わせてご覧ください。


一様分布
一様分布とは、ある区間における発生確率が全て同じとなる確率分布のことです。
例えば、サイコロの目のように全ての目が1/6の確率で出る事例やルーレットの目の事例など、身近なものも多くみられます。
ここでは、サイコロを10回振った場合の出た目の平均値を求める題材で、エクセルを用いて計算してみましょう。
1.母平均$μ$と母分散$σ^{2}$を計算する
一様分布の期待値(平均値)と分散は、以下の数式で求められます。
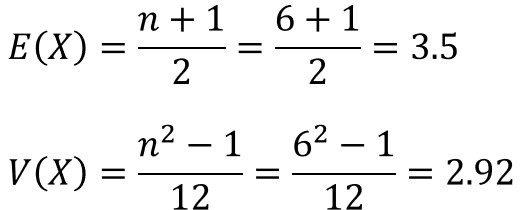
2.確率変数を乱数で発生させる
今回の事例では、サイコロの目が確率変数となり、1~6の範囲を取ります。
エクセルでは乱数を出力できる関数があり、これを用いるとランダムで確率変数を抽出でき、つまり、サイコロを疑似的に振ったことを模擬できるのです。
手順は簡単で、RANDBETWEEN関数で確率変数の最小値と最大値(今回は1と6)を指定するだけです。
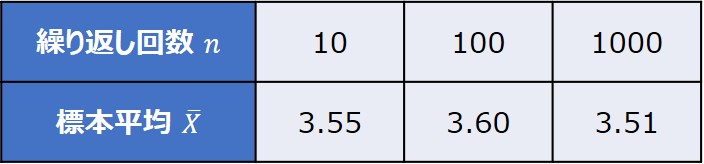
3.繰り返し回数nの違いを計算する
乱数10個を1回の試行として、出た目の平均値を求めます。
そして、これを10回、100回、1000回と繰り返した場合の平均値の分布をヒストグラムで見てみます。
シミュレーションの結果は以下の通り。
①:繰り返しが10回のヒストグラム
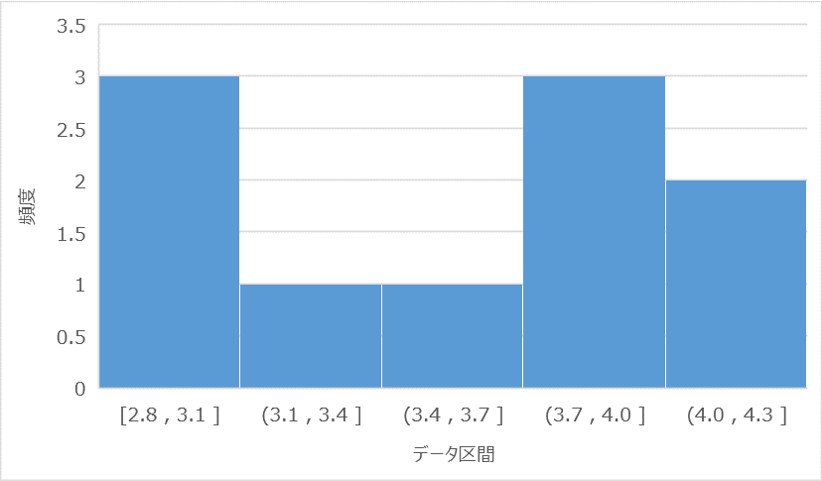
平均値の分布は中央の区間が低く、最も小さい区間の頻度が高い結果となりました。
まさに、たまたま出た目の偏りがあったというケースですね。
②:繰り返しが100回のヒストグラム
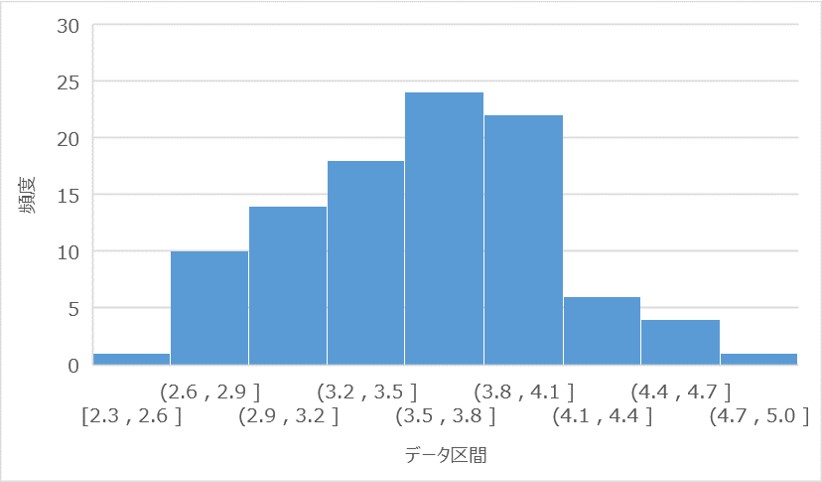
かなり、正規分布の形状に近づきましたが、ややピークから右の分布に偏りが見られます。
③:繰り返しが1000回のヒストグラム
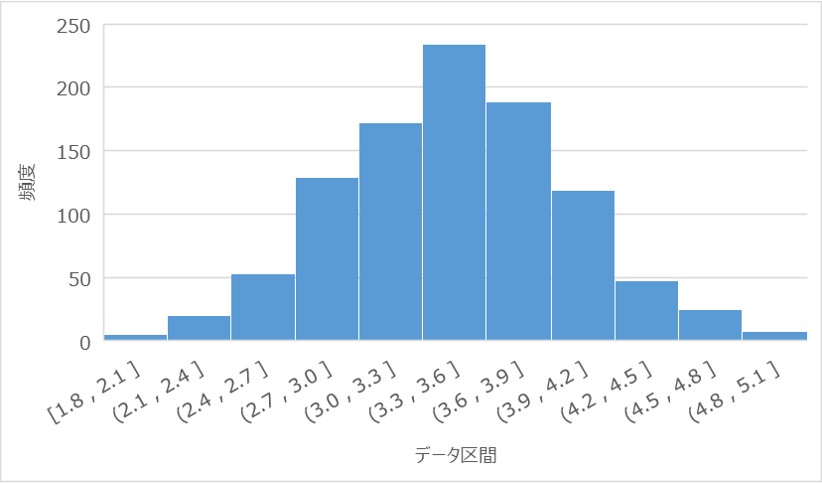
平均値も3.51とほぼ理論値に合致しており、分布の形状も左右対称でほぼ正規分布と言える状態です。
以下のグラフは、それぞれの試行回数における正規分布$N(μ, σ^{2}/n)$の確率密度関数の分布です。
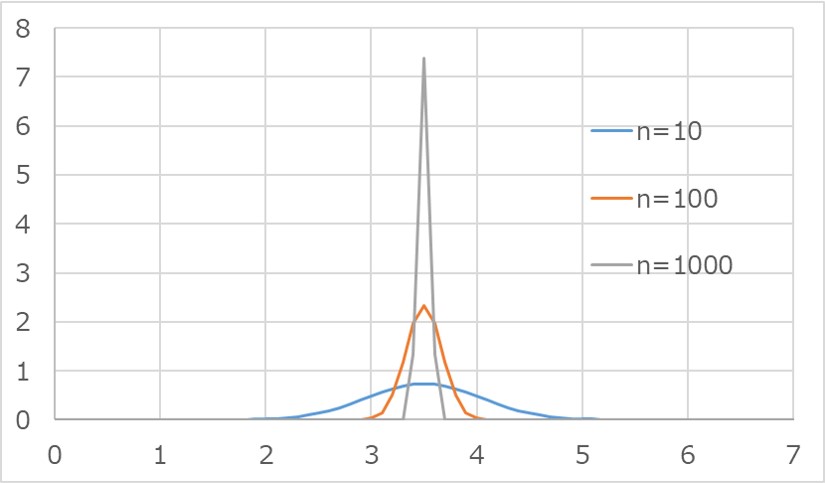
nが大きいほど、分布の広がりは小さくなり、シャープな形状になっていることが分かります。
つまり、標本平均が母平均から乖離する確率が低いことを表しており、まさに中心極限定理の定義を視覚的なイメージとして掴んでいただけたかと思います。

グラフを見れば本当に収束することが分かったよ
指数分布
もう一つ、指数分布を例に挙げてシミュレーションしてみます。
指数分布とは、とある事象の発生間隔を表す連続型の確率分布です。
例えば、とある店の来客の間隔や、とある製品が壊れる間隔、次に電話が鳴るまでの時間など、身近な事例に活用されることも多く、時間を確率変数に取ることが特徴です。
指数分布の確率密度関数は、以下のように定義されます。今回は、$λ=3$として計算してみます。
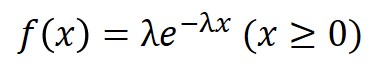
1.母平均$μ$と母分散$σ^{2}$を計算する
指数分布の期待値(平均値)と分散は、以下の数式で求められます。
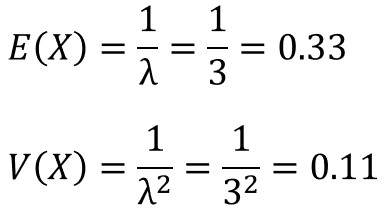
2.確率変数を乱数で発生させる
指数分布に従う確率変数を乱数で発生させるには、逆関数を利用します。
指数分布の累積分布関数は以下の数式で定義されます。
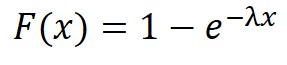
累積分布関数とは、確率変数がある値以下となる確率の関数のことで、0~1の範囲の値を取ります。
このF(x)の値を一様乱数(0~1の範囲で同じ確率で出現する乱数)として入力し、以下の数式で逆関数を計算することで、指数分布に従う乱数に変換できるのです。
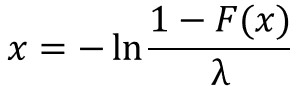
3.繰り返し回数nの違いを計算する
乱数10個を1回の試行として、出た値の平均値を求めます。
そして、これを10回、100回、1000回と繰り返した場合の平均値の分布をヒストグラムで見てみます。
シミュレーションの結果は以下の通り。
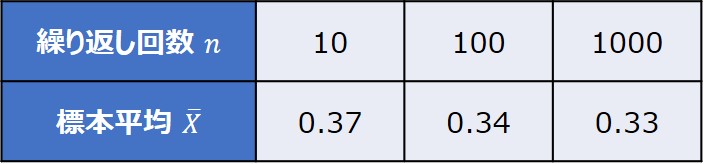
①:繰り返しが10回のヒストグラム
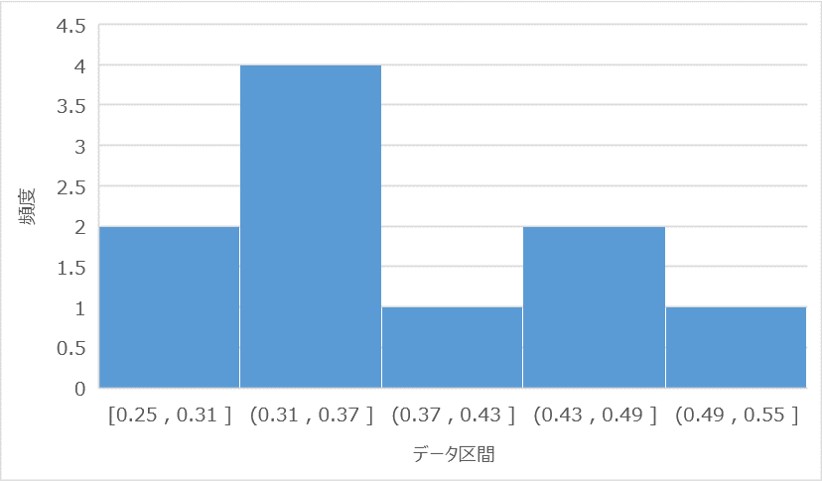
②:繰り返しが100回のヒストグラム
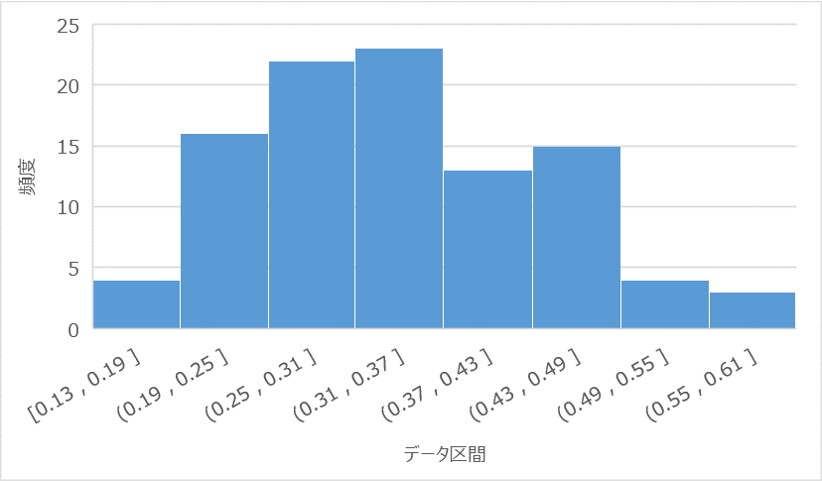
③:繰り返しが1000回のヒストグラム
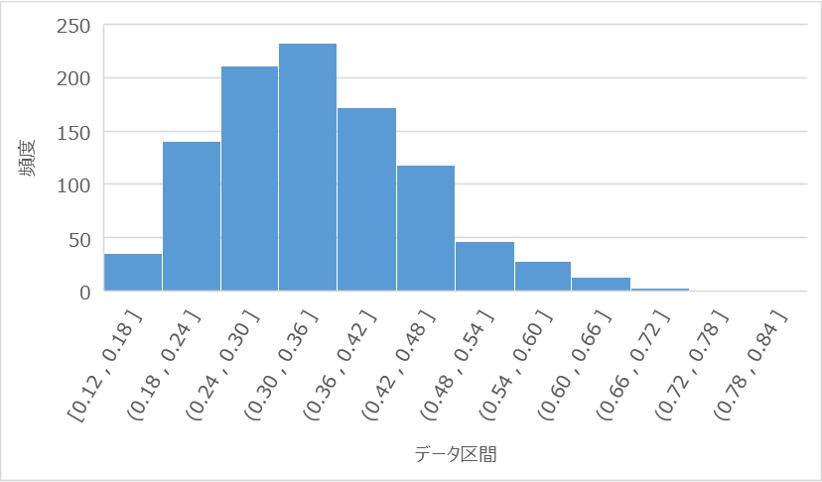
それぞれの試行回数における正規分布$N(μ, σ^{2}/n)$の確率密度関数の分布は以下の通り。
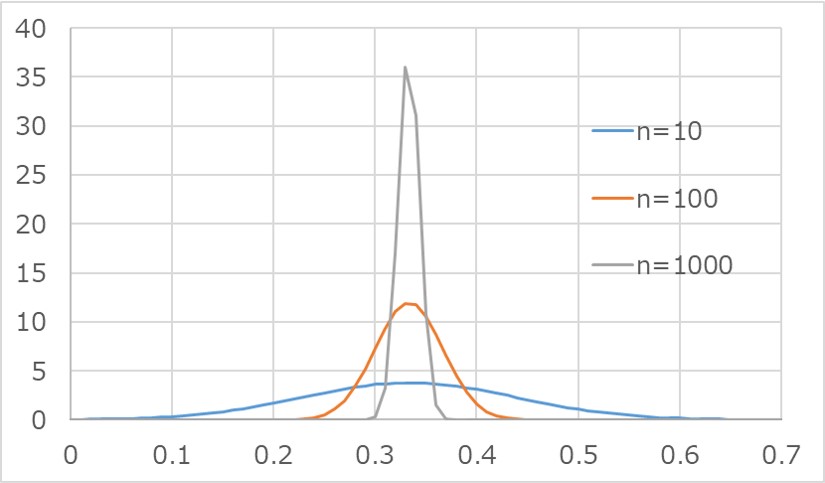
一様分布の場合と同様、nの増加に伴い、ばらつきが小さく理論値に収束していくことが分かります。

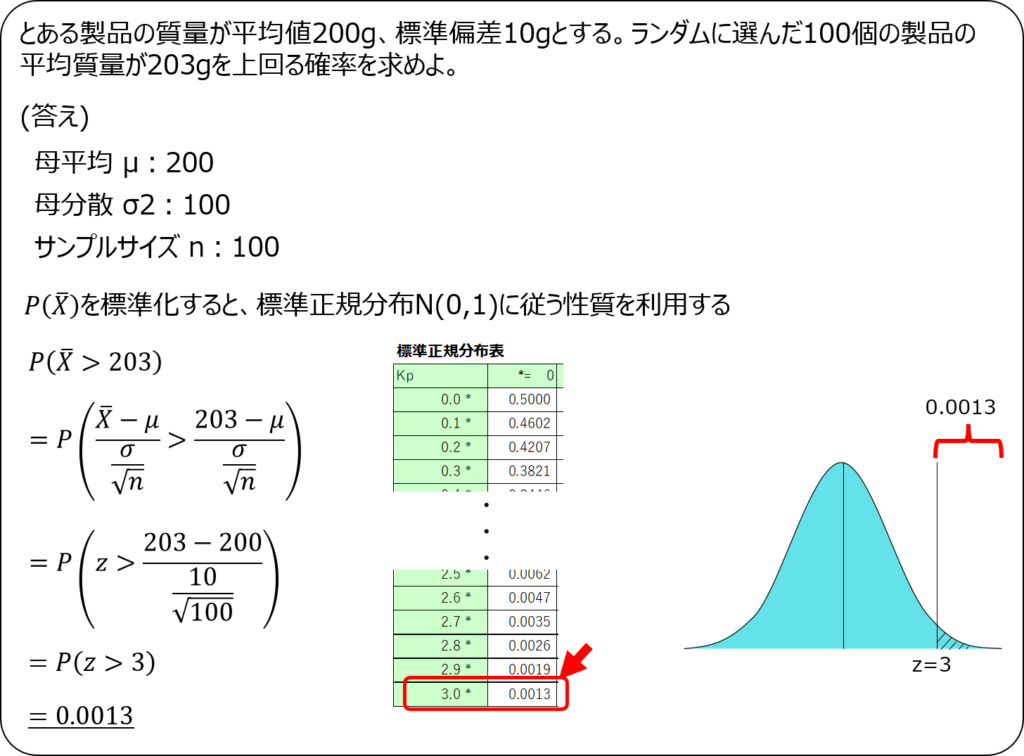
例題
まとめ
- 中心極限定理
⇒平均値$μ$、分散$σ^{2}$の確率分布から$n$個を抽出する際、標本平均$\bar{x}$は$n$が十分大きい場合において、正規分布$N(μ, σ^{2}/n)$に従うという定理 - 大数の法則
⇒サンプリング数$n$が十分に大きい場合に、標本平均$\bar{x}$は母平均$μ$に近づくという法則 - 中心極限定理を用いるメリット
⇒電卓やエクセルでは処理できないような複雑な計算が不要で、NORM.DIST関数や標準正規分布表から確率を簡単に求めることができる
中心極限定理は、名前はむずかしそうですが、定理の意味そのものは感覚的に理解しやすく、覚えておくと確率計算の簡略化に大変有効です。
乱数計算も簡単にできるので、一度、実際に計算して試してみてはいかがでしょうか。
最後まで読んでいただき、ありがとうございました。
この記事で紹介した中心極限定理は、統計的品質管理を実践する上での基本要素の一つです。
製造業に携わるエンジニアであれば、その他の統計的手法はもちろんのこと、品質管理、生産の基礎知識を幅広く身につけておく必要があります。
社内講座などの機会が設けられている場合は、ぜひ若手のうちから積極的に活用して受講することをおススメします。
ただ、多くの社員を対象とする社内講座の場合、皆さん一人ひとりのレベルに適した学習ができない場合もあります。
忙しい日々の限られた勉強の時間を最大限に活かすためにも、自分の教育プランは自分で管理することを意識して、能動的に学習することも検討してみてはいかがでしょうか。





コメント